Квантовая проводимость двумерного баллистического контакта

Рассмотрим двумерный баллистический контакт в случае, когда размер контакта существенно меньше фермиевской длины волны электрона. Пример такого контакта — контакты на гетероструктурах GaAs c высокой подвижностью при достаточно большом затворном напряжении.

Проводимость таких контактов теоретически вычислялась в нескольких работах. В работе [1] выводились волновые функции барьера с одиночным отверстием в трехмерном случае. Это делалось методом решения уравнений Лапласа в эллиптических координатах. В работе [2] был сделан ряд поправок к работе [1] и полученные волновые функции использовались для вычисления проводимости трехмерного квантового контакта, что давало результат G к (k F a) 6 , где a — характерный размер такого контакта.

Проводимость двумерного контакта вычислялась в [3], при этом двумерный контакт получался из трехмерного путем «склеивания», а геометрия области «склеивания» моделировалась отталкивательным дельта-потенциалом, равномерно распределенным по границе. В случае a ^ X f получалась сложная зависимость: G к (1 + 4/n ² [Y + ln(k F a/2)] ² ) ^-1 , хотя было бы логично ожидать, что с уменьшением размерности просто уменьшится показатель степенной зависимости от a. Похожий случай мы наблюдаем в квазиклассике. Согласно формуле Шарвина, проводимость пропорциональна размеру отверстия в двумерном случае и площади отверстия — в трехмерном (см. 3.20 и 3.21 из [4]).

Мы использовали для вычисления проводимости двумерного контакта стандартный метод Ландауэра [4]. Будем рассматривать следующую модель геометрии контакта. Две проводящие полуплоскости разделены непроницаемой диэлектрической перегородкой, в которой имеется прорезь размера 2a [5]. Пусть на контакт падают плоские волны. Рассмотрим одну из них: v n = exp(ik n y) (см. рис. 1). При прохождении контакта она рассеивается во множество плоских волн ^ _nm и дает прошедшую волну: ^2_m t _nm exp(ik _m y) = ^2_m ^ _nm . Введем коэффициент прохождения для каждой волны ψ _nm в виде отношения прошедшего и падающего потоков: T nm = j (^ _nm )/j(^ n ). Формула Ландауэра позволяет выразить проводимость через эти коэффициенты прохождения:

G =   X T nm .                              (1)

π ~ nm

В нашем случае n и m эквивалентны углам ϕk и ϕ, которые падающая и прошедшая волны соответственно образуют с осью OY , перпендикулярной линии диэлектрика, т. е. проводимость можно записать в виде

3 π/ 2          π/ 2

G = e- lim     d^ k k F     d^RT(^ k ,y),

π ~ R →∞

π/ 2          - π/ 2

где R = ^x2 + y2 — расстояние от центра контакта. Коэффициент прохождения равен отноше- нию потоков падающей и прошедшей волн:

T = Wt⁽W ^^Mw ,^) - ^ t ⁽ ^ k ,^)^< t ⁽ ^ k ,у) | К(№) V ^ i (^ k ) - ^ i (^ k ) V ^ * (^ k ) |

где ^ i = exp(ik x x + ik y y ) — падающая волна, a ^ t — прошедшая. Учитывая вид падающей волны, переписываем (3) в виде

T = К(V k ,V) V ^ t (V k ,V) - ^ t (V k ,V) V ^t* (V k ,V) | 2k F

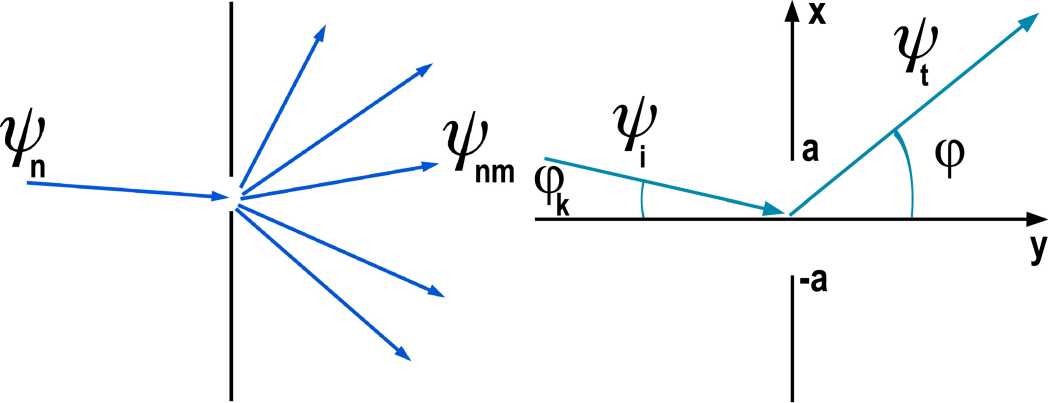
Рис. 1                                               Рис. 2

Найдем вид прошедшей волны ψ t . Для этого запишем уравнение Гельмгольца с граничными условиями для волновой функции в рассматриваемой нами геометрической системе (см. рис. 2):

( v ² + kF > = o,

^ | x G ( - a,a),y=0     ^{x ( x}, ^{0) .}

Здесь x(x,0) — некоторая неизвестная граничная функция на контакте, а функция ^ представляет собой сумму функции ^ ₀ = exp(ik x x)(exp(ik _y y ) + exp( - ik y y)) в отсутствие отверстия и поправки к ней ^ t при наличии отверстия: ^ = ^ ₀ + ^ t . Для ^ t система переписывается следующим

образом:

( v ² + k F м = o, ^ t | x G ( - a,a ) ,y =0    ^{x ( x}, ^{0) .}

Перейдем к фурье-образу:

X t (x,y) = j dk x exp( - ik _x x)^ t (k x ,y ).

Будем искать ^ _t в виде уходящей на бесконечность волны: ^ _t = c 1 exp( - ik y y ), где константа c 1 легко находится из граничных условий:

c i

j dx exp(ik x x )x(x 0 ,0).

Подставляя (8) в (7), приводим ψ _t к виду

^ t (x,y) = j dx x(x ,0)K (x,x,y ).

Появляющееся здесь ядро K (x, x ⁰ , y ) может быть вычислено через интегральные представления функций Бесселя [6]:

г k    H i ¹ ) (k F P(x - x ⁰ ) ² + y ² )

²          p(x - x ⁰ ) ² + y ²

. (10)

∞

K(x,x,y) = j ^n x exp(-ik x (x - x¹ ))exp(-i^k _F - k X y ) =

-∞

Таким образом, ^t выражается теперь только через неизвестную граничную функцию x(x, 0). Поэтому, записав непрерывность производной от функции ^ = ^0 + ^t на контакте (то есть при у = 0 и x € (-a,a)), можно получить интегральное уравнение на эту граничную функцию. Непрерывность производной выглядит следующим образом:

Ntpp,        ^d^ Q ^{( x,}y)        ^d^ t^{( x}, - у).

d          + dy         = dy          '                     ⁽¹¹⁾

что при подстановке ^ t из (9) и ^ q = exp(ik x x)(exp(ik y у) + exp( - ik y у)) дает нам следующее интегральное уравнение на неизвестную граничную функцию x(x,0):

Z dx 0 x(x 0 ,0) --i k F H ^{1 (k} F |x ——! = -ik y exp(ik x x).                (12)

2         | x - x ⁰ |

- a

Переходя к пределу ka ^ 1, сводим это уравнение к виду

a

J d ,. ■ п (x—xp)

- a

—ik y .

Интегрируя правую часть по частям и учитывая, что граничная функция зануляется на концах отверстия, сводим это уравнение к известному интегральному уравнению [7], что после всех интегрирований и упрощений дает

x(x^z,0) = ik y pa ² - x^{z 2} •

Подставляя (10) и (14) в (9), находим, наконец, ψ _t :

na ²      H'^kFF R)

^ t = -4- ^k y k F у ---R---

.

Функция (15) вычислена в приближении R ^ a, поскольку в (2) мы будем переходить к пределу R ^ то . Подставляем (15) в (4), и в полученном коэффициенте прохождения T(^ к ,^) переходим к ассимптотикам функций Ханкеля при k F R ^ 1. Полученный результат интегрируем в (2) и

окончательно находим

G = e ² — k > a ⁴ .

~ 32 F

Полученная нами зависимость проводимости от размеров отверстия G к (k F a) ⁴ не совпала с зависимостью G к (1 +4/t²[y + ln(k F a/2)] ² ) ^-1 , выведенной в работе [3]. Однако в пользу нашего результата говорит следующая физическая аналогия. Поскольку во всех упомянутых работах баллистический квантовый контакт моделируется отверстием с размерами много меньше длины волны, то можно провести параллель с рэлеевским рассеянием света на частицах размером много меньше длины волны. Интенсивность рассеяния света на такой частице пропорциональна квадрату объема частицы [8], что дает зависимость (F f a) ⁶ в трехмерном случае (аналогия с работой [2]) и (F f a) ⁴ в двумерном (аналогия с нашей работой)

Работа выполнена при финансовой поддержке фонда «Династия» и Российского фонда фундаментальных исследований (проект № 10-02-00814-а).