Квантовая релятивистская информатика. Ч. 1: модели физических объектов и квантовые релятивистские эффекты в интеллектуальных вычислениях
Автор: Ульянов Сергей Викторович, Решетников Геннадий Павлович, Бархатова Ирина Александровна, Албу Вячеслав Андреевич, Аверкин Алексей Николаевич, Токарева Надежда Александровна
Журнал: Сетевое научное издание «Системный анализ в науке и образовании» @journal-sanse
Статья в выпуске: 4, 2013 года.
Бесплатный доступ
Дано описание моделей физических объектов квантовой релятивистской информатики. Отмечены особенности применения квантовых вычислений и физические ограничения на разработку программно-аппаратной поддержки в задачах квантовой информатики.
Квантовая релятивистская информатика, нанотехнологии, квантовые вычисления
Короткий адрес: https://sciup.org/14123233
IDR: 14123233
Текст научной статьи Квантовая релятивистская информатика. Ч. 1: модели физических объектов и квантовые релятивистские эффекты в интеллектуальных вычислениях
Разработка и развитие новых информационных технологий (ИТ) основаны на достижениях фундаментальных наук в области физики, математики, биофизики, нейрофизиологии мозга, биологии, теории искусственного интеллекта, теории управления, теории сложных слабоструктурированных систем и мн. др.
Однако многие из полученных результатов в области фундаментальных наук не востребованы инженерией системного проектирования в силу трудности восприятия и практического применения данного результата или, с другой стороны, недооценкой менеджерами промышленных компаний прикладной стороны и коммерческой привлекательности полученного интеллектуального продукта на рынке ИТ.
Рассмотрим актуальность обсуждаемой проблемы и коммерческую привлекательность разрабатываемых интеллектуальных продуктов на современном этапе развития наукоёмких ИТ с позиции инженерного менеджмента, основанного на знаниях. Содержательная часть и доказательная база наукоёмкости рассматриваемых моделей ИТ приведены ниже.
Примером одной из практических целей разработки наукоемких ИТ является коммерчески привлекательный и конкурентно способный программно-аппаратный комплекс, а также промышленный инструментарий проектирования интеллектуальных систем управления (ИСУ) физическими моделями сложных слабоструктурированных объектов в нештатных ситуациях. Проектирование интеллектуальных встраиваемых контроллеров для надежной корректировки ошибок и восстановления информации в процессах обработки больших массивов данных физических экспериментов является еще одним примером подобного рода интеллектуальных продуктов. Исследования и практика разработки систем управления физическим экспериментом показали следующее: проектирование, развитие и реализация эффективных высоких наукоемких ИТ (создаваемых в различных областях науки и техники) неразрывно связаны с необходимостью развития и повышения уровня интеллектуальности используемых моделей процессов и систем управления, объективно учитывающих в законах эволюции контекстуально-зависимые физические эффекты, термодинамические ограничения и информационные границы, реально существующие в конкретных моделях реальных объектов.
В данном разделе рассмотрена проблемно-ориентированная область разработки наукоемких квантовых релятивистских ИТ: прорывные инновационные ИТ интеллектуального управления квантовыми и релятивистскими системами в компьютерных нанотехнологиях с целью показать перспективность данной технологии при разработке коммерчески привлекательных интеллектуальных продуктов в области робототехники, космической техники, квантового управления в нанотехнологии, информационно-управляющих комплексов социально и экономически значимых объектов, квантовой релятивистской криптографии и квантовых облачных вычислений «вслепую» ( quantum blind cloud computing ) для защиты информации и безопасности систем, квантовый интернет и др.
Одно из обстоятельств закономерного интенсивного развития наукоемких ИТ интеллектуального робастного управления в компьютерных нанотехнологиях связано с известным фактом появившейся возможности для системной инженерии доступного (для использования в проектировании) изложения квантовых и релятивистских макро эффектов, которые лежат в основе управления как космическими летательными аппаратами (КЛА), так и квантовыми системами, находящихся под действием слабых гравитационных полей.
С точки зрения теории управления и системной инженерии, проектирование, например, КЛА, движущегося в искривленном пространстве-времени под действием солнечного ветра или мелких метеоритов как случайных воздействий, или проектирование устройств квантовой памяти (или квантового гироскопа) на основе движения квантовой частицы (со спином ½ или без спина) в слабом гравитационном поле под воздействием случайных возмущений, рассматривается с позиции описания данных устройств как объектов управления (ОУ).
В обоих случаях ОУ находятся в пространстве-времени с определенной метрикой и геометрией, в гравитационном поле под воздействием внешних случайных сил и должны быть описаны соответствующими математическими моделями, которые содержат надлежащие физические эффекты. Проявление (не)учтенных в моделях релятивистских и квантовых эффектов отражается на качестве интеллектуального управления, а базы знаний ИСУ проектируются с учетом физической сущности динамического поведения ОУ.
До настоящего времени физическая теория моделей управления находится в стадии своего становления. Период переосмысления принципов системной инженерией о необходимости учета такого рода эффектов осуществлен благодаря результатам работ Эйнштейна, Дирака, Фейнмана,
Алферова, Манина, Дейча, Шора, Гровера, Прескиля, Самойленко и мн. др. в области разработки основ квантовой инженерии, а также Синга, Котельникова, Уилла, Седова, Эшби, Брумберга, Копейкина и мн. др. в области релятивистской небесной механики и релятивистской навигации КЛА.
Необходимость разработки ИТ с учетом квантовых эффектов продиктована также объективной формой (подтвержденная практикой) законов Мура (1965 г.) и Ландауэра (1961 г.), которые показали направление развития микроминиатюризации элементной базы электронных устройств, эволюция которой привела к необходимости учета ограничений в процессах проектирования потерь от тепловых и квантовых флуктуаций, а также физической меры стоимости быстродействия и производительности квантовых вычислительных процессов.
Группой Котельникова проведена большая работа по радиолокации измерения орбитального движения планет Солнечной системы независимо от модели пространственно-временного континуума и показано, что без учета релятивистских поправок в рамках ньютоновой небесной механики промах КЛА при запуске на планеты может достигать от 200 до 500 км.
Разработка логически непротиворечивых и адекватных (корректных) моделей объектов управления (ОУ) с целью эффективной реализации интеллектуальных систем управления (ИСУ) новыми видами современной техники является одной из актуальных проблем для современного этапа развития теории и систем управления. Диапазон применения современных ИСУ физическим экспериментом включает в себя, например, от сложных макрообъектов управления типа КЛА до квантовомеханических моделей нанотехнологий (на микро- и наноуровнях) с необходимостью учета релятивистских и квантовых эффектов общей теории относительности и квантовой механики соответственно.
Выбор корректной модели, в первую очередь ОУ минимальной алгоритмической сложности, является важной для практики задачей. Однако критерий минимальной алгоритмической сложности при выборе метода описания модели ОУ требует уточнения и физического обоснования.
Примером могут служить реальные факты.
Рассмотрим ранее упомянутый пример результатов группы Котельникова. Так при оценке возможных отклонений траекторий движения КЛА (как ОУ в задаче инерциальной навигации), вычисленных по классической теории, от траекторий движения планет Солнечной системы, экспериментально установленных радиолокационными методами, было выявлено следующее обстоятельство. Для гелиоцентрических расстояний планеты Марс отклонение экспериментальных данных составляет 150 км по отношению к расчетным данным, основанным на классических теориях движения планет, и планеты Венера до 500 км соответственно с ошибкой измерения до 10 м (на протяжении времени наблюдений в 20 лет)2. Таким образом, модель движения планет с учетом релятивистских эффектов является корректной для навигации КЛА даже в пределах Солнечной системы, несмотря на широко распространенное интуитивное представление о пространственновременном континууме в классической механике инерциальной навигации КЛА и Галилеевой группой преобразования.
Квантовые модели конденсата Бозе-Эйнштейна на основе нелинейной модели уравнения Шредингера (типа уравнения Питаевского-Гросса) для моделирования наноструктур или модели уравнения типа Гинзбурга–Ландау и мн. др. являются важным примером необходимости учета квантовых эффектов в математических моделях ОУ нанотехнологий и т.п. В тоже время уравнение Гросса-Питаевского и Шредингера успешно применяется в задачах разработки квантового поискового алгоритма в неструктурированных базах данных3.
Необходимость учета квантовых эффектов и квантовой логики привело к необходимости развития квантовой информатики4,5,6,7,8,9,10. Системный анализ разработки и проектирования ИСУ для многих моделей такого рода ОУ тесно связан с необходимостью корректного учета существующих физических ограничений. Ограничения на описание динамического поведения сложного физического ОУ (в частности, на предельную точность процессов измерений и управления; выбор модели пространства-времени и др.) накладываются известными физическими законами (из таких дисциплин как статистическая механика, теория относительности, термодинамика, теория информации и квантовая механика [1]).
Примером таких ограничений являются следующие: термодинамические ограничения на физическую реализацию математических моделей ОУ; различные типы обобщенных информационных соотношений неопределенности Гейзенберга; квантовые ограничения на пропускную способность передачи информации с учетом термодинамических флуктуаций; квантовые оценки предельных возможностей точности измерений параметров ОУ и процессов управления в нанотехнологиях и мн. др.
Данные ограничения должны быть учтены в алгоритме проектирования объективных баз знаний (БЗ) в ИСУ. Повышение требований к точности управления в нанотехнологиях с учетом квантовых эффектов (например, исполнительных устройств – квантовых электромеханических систем [2]) приводит к логическому переходу в квантовую область процессов измерений и управления на атомно-молекулярном уровне [3-5].
В свою очередь, происходит неизбежный пересмотр физических основ самой теории управления.
Аналогичный результат получен при разработке основ квантовой теории информации и квантовых вычислений, приведших к пересмотру аксиоматики моделей физических вычислений и логическому обобщению тезиса Тьюринга-Черча. Многие из перечисленных проблем физической теории и систем управления рассматривались ранее. Были рассмотрены конкретные примеры и получены важные выводы о необходимости учета физической природы самого ОУ в структуре и предельных возможностей процессов управления.
Роль корректной интерпретации физической и математической моделей эксперимента11, взаимосвязь с необходимым уровнем полноты извлекаемых при измерении знаний, алгоритмической сложности математических моделей ОУ и влияние перечисленных факторов на робастность формируемой БЗ в ИСУ (функционирующих в динамически изменяющихся непредвиденных ситуациях управления) в теории управления практически не исследовались. Принципиальное значение при формировании объективных знаний имеет глобальная оценка функциональной реализуемости аппроксимации моделей при наличии логико-информационных границ и физических (термодинамических, квантово-релятивистских) ограничений на описание реальных нелинейных ОУ. На основе достоверности извлекаемого количества информации определяется информационная оценка приращения риска (статистической корректности) формируемого описания модели ОУ, и границ её применимости.
В данной работе роль особенностей физических ограничений и информационных границ рассматривается с позиции специфики новой проблемы теорий искусственного интеллекта и
-
4 Яковлев В.П., Кондрашин М.П. Элементы квантовой информатики. – М.: МИФИ, 2004. – С. 80.
-
5 Кулик С.Д., Берков А.В., Яковлев В.П. Введение в теорию квантовых вычислений (методы квантовой механики в кибернетике): учебное пособие. – В 2 кн. – М.: МИФИ, 2008. – С. 212.
-
6 Кронберг Д.А., Ожигов Ю.И., Чернявский А.Ю. Квантовая информатика и квантовый компьютер: учебное пособие. – М.: МГУ, 2008; Алгебраический аппарат квантовой информатики: учебное пособие. – М.: МГУ, 2008.
-
7 Чивилихин С.А. Квантовая информатика: Учебное пособие. – СПб.: СПбГУ ИТМО. – 2009. – С. 80; Квантовая информатика: Лабораторный практикум. – СПб.: СПбГУ ИТМО, 2009.
-
8 Калачёв А.А. Квантовая информатика в задачах: учебно-методическое пособие. – Каз.: КГУ. – 2012. – С. 48.
-
9 Соколов А.И. Элементы квантовой информатики: учебное пособие. – СПб..: СПбГУ, 2012. – С. 72.
-
10 Иванов М.Г. Как понимать квантовую механику. – М.: Ижевск: НИЦ «Регулярная и хаотическая динамика». – 2012. – C. 516.
-
11 Пытьев Ю. П. Математические методы интерпретации эксперимента. – М: Высшая школа, 1989.
процессов интеллектуального управления: возможности формирования объективных баз знаний (БЗ) в процессе проектирования робастных ИСУ путем извлечения знаний и ценной информации из динамического поведения модели самого физического ОУ.
Корректное описание модели ОУ существенно влияет на качество формируемой БЗ и, таким образом, на эффективность применения разрабатываемых структур ИСУ. В частности, в данной работе описаны неклассические логические, квантовые и релятивистские эффекты, влияющие на описание модели ОУ и оптимальное управление динамическими системами. Дана информационная оценка (нижних и верхних) границ риска, возникающего из-за необходимости учета ограниченных возможностей информированности исследователя о свойствах ОУ и влияющего на качество разработки математической модели исследуемой системы.
Приведены термодинамические условия на интерпретацию физической реализуемости (инвариантных к возмущениям) динамических систем управления, на точность аппроксимации модели ОУ и полноту формирования робастных БЗ в ИСУ с глубинным представлением знаний.
Однако прогресс развития и создания подобного рода ИТ сталкивается с трудностью восприятия специалистами логики интерпретации квантовых и релятивистских эффектов, которые можно использовать для создания технологии проектирования новых видов компьютеров типа квантового компьютера (включая новые виды моделей квантовой информатики, квантового программирования, технологий интеллектуальных вычислений таких как квантовые мягкие вычисления, квантовые генетические и иммунные алгоритмы, квантовые нейронные сети, ДНК вычисления и др.) и применять на практике управления сложными ОУ в непредвиденных ситуациях управления.
Важным (и необходимым для практики) является методологический аспект: корректность, сложность и точность аппроксимации подробного описания (и доступного для специалистов в области теории и систем управления) физических и математических моделей ОУ на основе релятивистской квантовой механики.
Слабоструктурированная модель ОУ является источником извлечения знаний и используется в интеллектуальных квантовых мягких вычислениях для проектирования моделей робастных ИСУ в непредвиденных ситуациях управления физическим экспериментом.
Необходимость данного описания объясняется во многом трудностями восприятия квантовых и релятивистских эффектов, результатов квантовой и релятивистской теории информации и возникающих при физической интерпретации логических «парадоксов», противоречащих выводам классической Булевой логики.
Переход от традиционных методов к новым инновационным образовательным технологиям доступного изложения основ квантовой механики и теории относительности связан также с фактом существования психологического и информационного барьеров восприятия инженерной аудиторией физической модели интерпретации логики событий в теории относительности и математического аппарата квантовой механики, «парадоксов» выводов квантовой и релятивистской логики.
Данный факт отражается непосредственно, например, при изложении решений, получаемых на основе квантовых алгоритмов, или при выводе уравнений движения КЛА и квантовой частицы со спином при воздействии случайных возмущений в искривленном пространстве-времени.
Поэтому для разработки прикладных моделей новых видов интеллектуальных вычислений и их эффективного применения в прикладных задачах управления возникла необходимость формирования новых прорывных образовательных программ с целью более детального и доступного изложения основ квантовой механики, используемых, например, в квантовой информатике на основе теории квантовых вычислений и квантовых алгоритмов.
Здесь рассмотрим только отдельные иллюстративные примеры и особенности роли квантовой информатики в разработке ИТ интеллектуального управления квантовыми и релятивистскими системами. Более детально данные вопросы освещены в последующих работах после изложения необходимых сведений из указанных прикладных проблемно-ориентированных областей квантовой релятивистской информатики. Отметим, что публикаций (доступных в сети интернет) в области квантовой информатики достаточно много. Поэтому освещаются менее известные в литературе модели и эффекты прикладной квантовой информатики, необходимые для компьютерных технологий (computer science).
Этот факт объясняется бурным развитием данной прикладной области наукоёмких коммерчески привлекательных ИТ и существенным отставанием отечественных образовательных программ от освещения современных результатов в области информатики и управления.
Квантовые эффекты в системном проектировании микро - и наноустройств: от микроэлектроники к наноэлектронике
Изменение размерности ОУ или увеличение плотности элементов на платах радиоэлектронной аппаратуры (рис. 1) связано с изменением физической модели и ее интерпретации, что приводит к достижению квантового предела xp принципа неопределенности Гейзенберга12 (рис. 2).
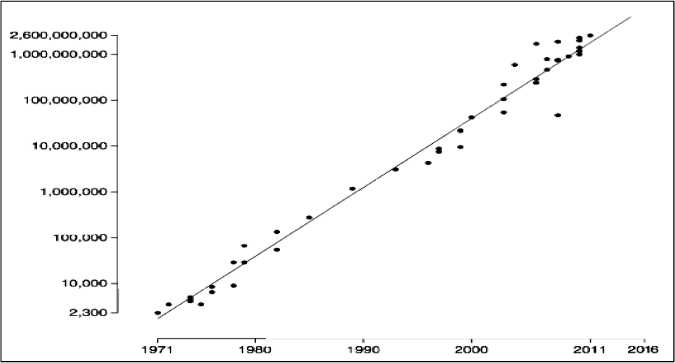
Рис. 1. Закон Мура возрастания плотности размещения элементов
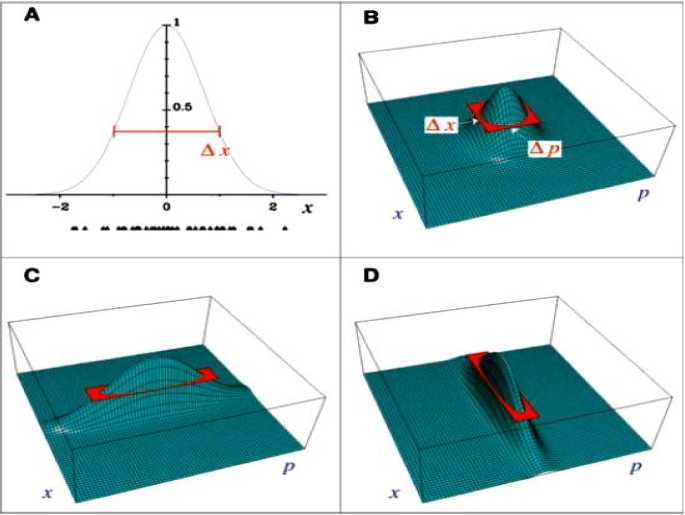
Рис. 2. Иллюстрация принципа неопределенности Гейзенберга
Наноэлектромеханические (NEMS – nano-electromechanical systems) и микромеханические (MEMS – micro-electromechanical systems) системы представляют собой яркий пример проявления квантовых эффектов: возможности реализации на малых расстояниях квантовой суперпозиции из классических состояний и достижения указанных квантовых пределов точности измерений.
На рис. 3 представлены примеры MEMS/NEMS устройств, в которых проявляются эффекты квантовой суперпозиции [2-17].
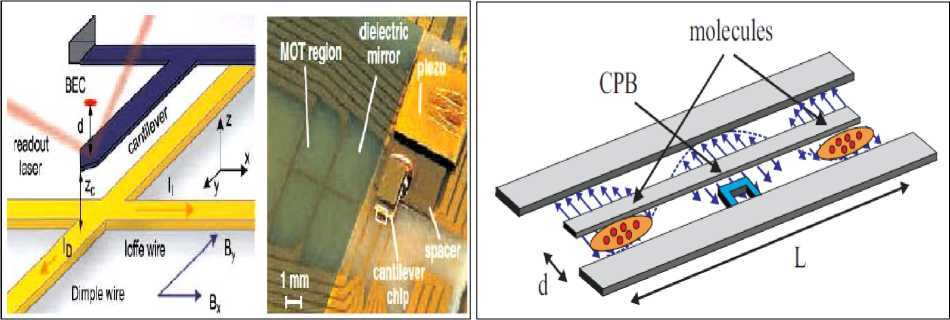
-
(а) (б)
Рис. 3. Конденсат Бозе-Эйнштейна на атомном чипе, встроенном в консоль [2]
-
(а) - движение консоли воспроизводит потенциал атомов, которые приводятся в связанное движение в консоли (слева - вид устройства; вибрации консоли с атомами регистрируются с помощью луча лазера; справа - фотография устройства);
-
(б) -блок формирования кубита на паре Купера и ансамбле поляризованных молекул (связанных состояний в микроволновой полосе фотонов. Строгая связанность состояний достигается на квазиодномерной структуре длиной порядка см и шириной порядка мкм) [17])
Изучение квантовых эффектов в сверхтонких полупроводниковых гетероструктурах дало толчок появлению нового класса полупроводниковых приборов – резонансных туннельных диодов (РТД) и транзисторов (РТТ), обладающих высоким быстродействием (предельные частоты 1012 Гц). Обсуждаются широко проблемы создания квантовых интегральных схем и квантового компьютера, основными элементами которых станут квантовые точки.
Квантовые проводники, квантовые ямы, транзисторные структуры на основе квантовых размерных эффектов и устройств с управляемой интерференцией электронов [18-23].
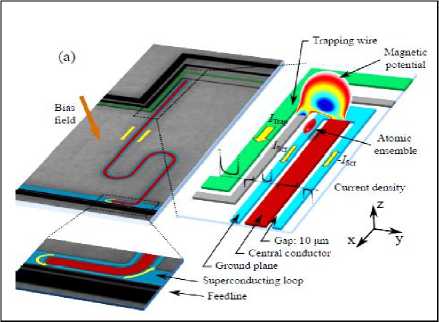
На рис. 4 показаны схематично способы формирования квантового бита13 на основе квантовых резонаторов как основного элемента квантовых ИТ.
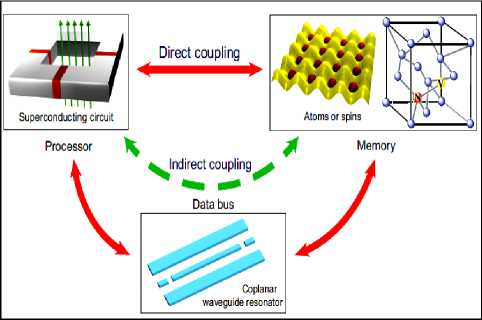
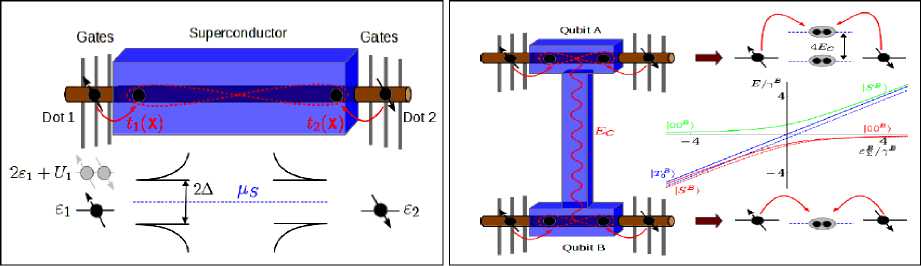
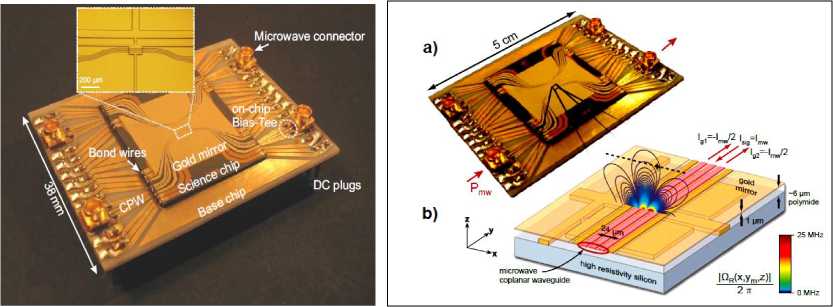
На рис. 5 (а, б, в) показана схема квантового компьютера с новыми видами элементной базы14,15,16,17 на сверхпроводниках и конденсате Бозе-Эйнштейна с квантово-механическими макроэффектами, позволяющие реализовать многие, ранее не реализуемые по техническим и алгоритмическим причинам, классические задачи.
Основу развивающейся наноэлектроники составляют структуры, состоящие из чередующихся полупроводниковых слоев с различными электрофизическими характеристиками.
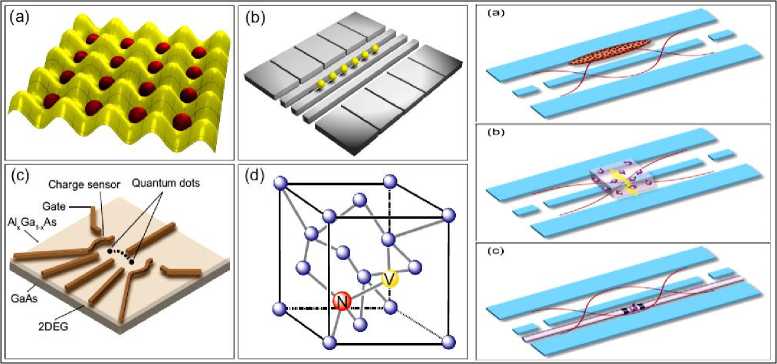
Рис. 4. Схемы формирования квантовых битов на основе нанотехнологий
(а)
(б)
(в)
(г)
Рис. 5. Схема квантового резонатора (а) и квантового компьютера (б) на сверпроводящих элементах и шиной обмена данными на компланарном волноводном квантовом резонаторе (в), вид атомного чипа (г)
Подобные рассмотренным выше структуры отличаются от однородных полупроводников наличием резких изменений потенциалов. Наиболее часто для описания электронных свойств многослойных структур используют метод огибающих волновых функций, в котором в области каждого слоя влияние его периодического потенциала сводится к подстановке в оператор кинетической энергии эффективной массы, а изменения законов дисперсии на гетерограницах играют роль эффективных потенциалов.
Поэтому многие задачи оценки особенностей энергетического спектра и исследования движения частиц сводятся к исследованию поведения квантовых уравнений частиц в системах с различными видами потенциальных барьеров [18-24].
Рассмотрим теперь на примерах вопросы о необходимости учета квантовых и релятивистских ограничений на физические и математические модели ОУ18.
Корректность моделей ОУ: Квантовые и релятивистские ограничения
Роль и влияние геометрии пространства-времени и релятивистских ограничений на корректность описания моделей ОУ отмечалась многими исследователями. Рассмотрим также аналогичные ограничения с позиции принципов квантовой и релятивистской механики.
– Корректность идентификации моделей ОУ. В общей теории динамических систем в ряде случаев оптимальные статистические процедуры для Гауссовских случайных полей оказываются, как правило, линейными. Для стационарных полей линейные статистические задачи приводят к исследованию уравнений Фредгольма 1-го рода типа:
t yt=^kt-sxsds, t e 0, T , x, y = 0
и являются (для идентификации ОУ или его входного сигнала [ x t , kt ]) некорректными задачами по Тихонову. Учет квантовой природы описываемых полей (например, бозонных) приводит к рассмотрению интегрального уравнения Фредгольма 2-го рода типа [25]:
t y t x t k t s x s ds, t 0,T , x, y i , где – постоянная Планка. Таким образом, учет квантовой природы физического поля (квантовые ограничения в виде некоммутативности наблюдаемых) приводит к естественной регуляризации некорректных задач, исследуемых в теории управления традиционными ОУ.
-
- Квантовые ограничения на пропускную способность канала передачи информации. В классической теории информации К. Шенноном получено выражение пропускной способности
канала связи с соотношение P / N (сигнал/шум) и полосой пропускания W следующего вида:
P
CW ln 1 . Из данного выражения следует, что при N 0 величина C , что физически
N нереализуемо. Для квантового канала передачи информации с учетом квантовых флуктуаций для
P
, где N 0 –
пропускной способности C имеем следующее выражение [26]: CW ln 1
NN 0
P
, т.е., является
интенсивность квантового шума. Таким образом, при N 0, lim CW ln 1
T 0
T 0 N 0
величиной ограниченной.
Рассмотрим теперь особенности влияния релятивистских ограничений на выбор модели ОУ.
-
- Релятивистские ограничения и корректность модели ОУ. Выбор физического базиса проведения эксперимента и определение математического способа (задания критерия корректного описания) модели ОУ существенно влияют на качество интерпретации результата процесса обработки экспериментальных данных и извлечения объективных знаний из динамического поведения самого ОУ.
Пример 1: Движение заряженной частицы вдоль релятивистского брахистохрона с учетом излучения мощности в заданном электрическом поле. Мощность Pt излучаемой энергии заряженной v2 2
, т.е., при vc (скоро-
частицы (например, в синхротроне) пропорциональна множителю 1
c стях движения, близких к скорости света) потери энергии на излучение могут быть весьма большими. В случае релятивистского брахистохрона, соответствующая величина Pt имеет вид:
2 q
Pt c 1
v 2 t
v 2 t
, что справедливо для произвольной орбиты с параметрами q и
v 2 t
2 c
. Таким образом, в рассмотренном
2 q
. В случае замкнутой орбиты имеем: P t c 1
случае потеря энергии на излучение (при vc ) стремятся к минимуму и решение задачи (без учета потерь на диссипативные процессы) оптимальны.
Рассмотрим и сравним аналогичные результаты для релятивистского таутохрона .
В этом случае выражение для рассеяния энергии имеет вид
P t 2 q2 2
34 c3
v2 t
1 c 2
2 1 4 2 2
c
1cv2
,
где имеет место соотношение 2 2 s 2 2 , v x i y j x i s j .
Таким образом, результат существенно отличается от случая релятивистского брахистохрона19.
Следовательно, более корректный учет физической особенности движения релятивистской системы также может приводить непосредственно к оптимальным решениям.
Квантовые эксперименты проверки гравитационных эффектов. Проверка корректности моделей квантовой теории и теории относительности проводилось в рамках нерелятивистской теории гравитации или без учета квантовых эффектов на малых расстояниях соответственно. Совместное тестирование привело к проблеме разработки квантовой теории гравитации. Особое значение решение данной проблемы имеет для построения корректных моделей новых объектов и ИТ, основанных на физических и логических эффектах релятивистских, квантовых и термодинамических теориях динамических систем. Так, например, развитие и создание новых методов физического эксперимента и систем проверки фундаментальных принципов квантовой информации передачи данных в космическом пространстве привело к необходимости переосмысления взаимоотношений квантовой теории и общей теории относительности (теории гравитации) 20.
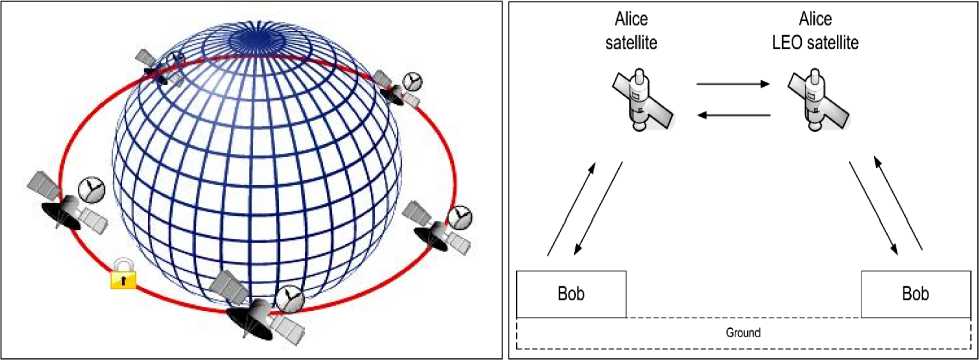
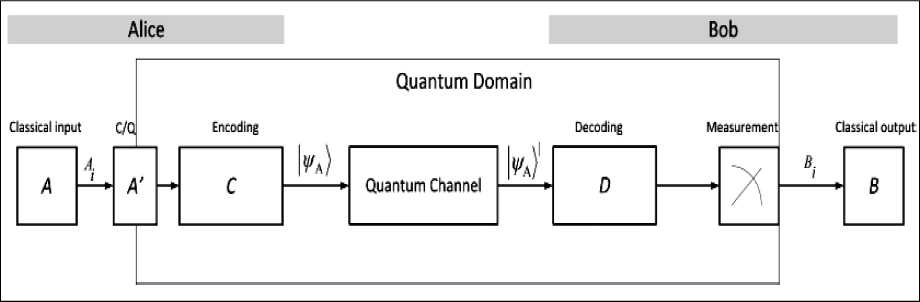
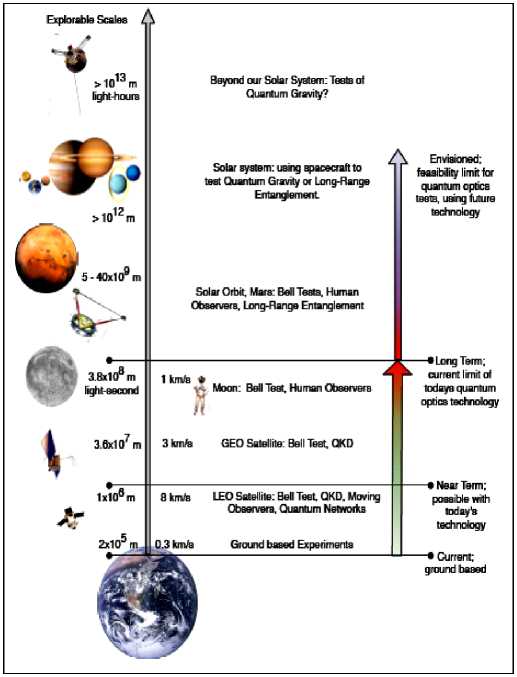
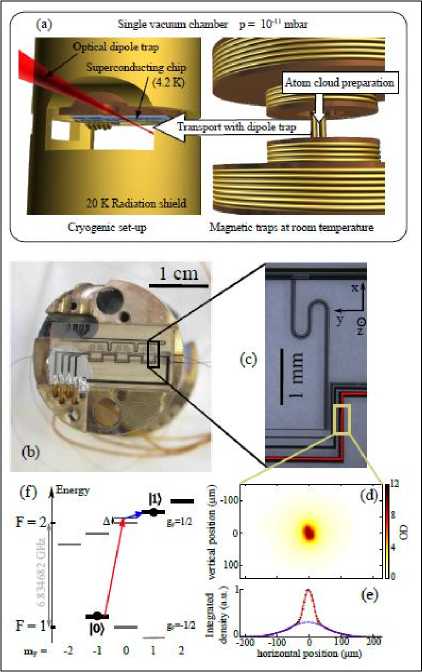
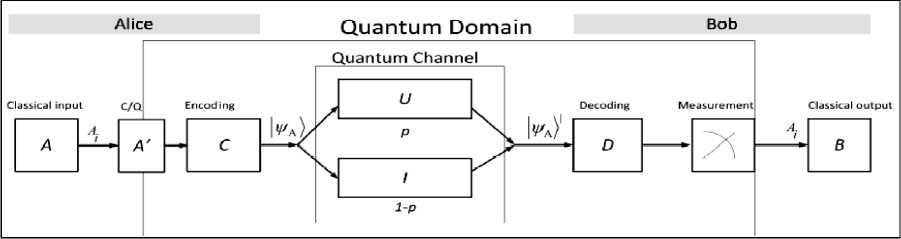
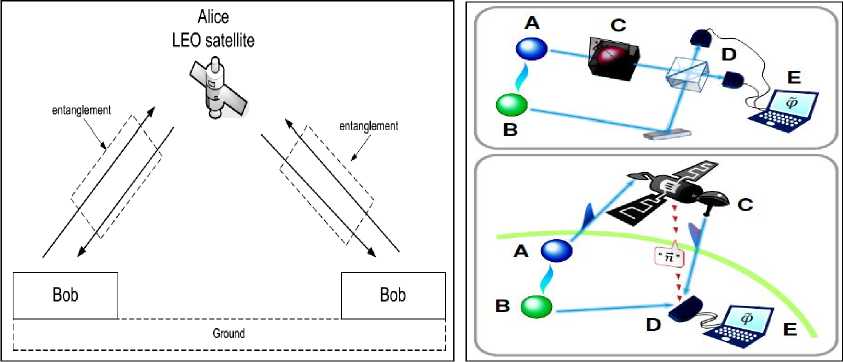
Для примера на рис. 6, а показана схема экспериментальной проверки фундаментальных теорий с целью выявления и описания границ применимости и возможных практических приложений.
(а)
(б)
(в)
Рис. 6. Схема тестирования фундаментальных теорий (а); квантового резонатора (б) и обработки информации в сети квантовых часов на борту искусственных спутников Земли с квантовыми облачными вычислениями «вслепую» с применением запутанных состояний (в)
На рис. 6, б приведена схема разработки и иллюстрация принципа работы квантового резонатора на атом-чипе как базового элемента многих микро- и наноэлектромеханических устройств, используемых в современном приборостроении и включающих в себя многие из перечисленных квантовых и релятивистских эффектов21.
На рис. 6, в приведена схема обработки информации в сети квантовых часов на борту искусственных спутников Земли с использованием квантовых каналов передачи и защиты данных на основе запутанных состояний в квантовых облачных вычислениях «вслепую» (quantum blind cloud computing) 22, 23, 24. Такие сложные аппаратно-программные комплексы представляют собой интеллектуальные наукоемкие ИТ обработки больших массивов информации с высокой точностью и требуют для своего создания самых современных знаний из области физики, механики и теории управления за счет разработки новых прорывных технологий образовательных процессов.
Здесь ограничимся только иллюстрацией особенностей учета релятивистских и квантовых эффектов в квантовой релятивистской информатики для обработки и физической интерпретации результатов физических экспериментов с целью пояснения необходимости углубленного изучения основ квантовой релятивистской механики при разработке новых моделей физических объектов.
Прежде чем изложить дальше материал, рассмотрим вспомогательный поучительный пример определения запутанных состояний без привлечения понятий квантовой механики.
Запутанные состояния являются важным физическим ресурсом квантовых вычислений и исследование таких состояний имеет важное значение для квантовой информации.
Пример 2: Принцип дополнительности , запутанные состояния и комплексные вероятности .
Определим для N событий Ai i е 1,2, , N пространства выборок S с определенными функциями распределения вероятностей Ai,i е 1,2, , N и зададим N комплексных функций:
^ Ai = аiejiP A eji,iе 1,2, ,N(1)
с модулями PAi и фазамиф , для которых для события A без потери общности задающая фаза ф 0 . В теории вероятностей для независимых событий A,A, выполняется правило следующего вида: P иAiP Aiи iN
PA A ...и A
NN
=ЕP Ai -ЕP Ai Aj i1 ij
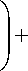
N
+уPAпAпA + ...+ -1N1PA AП...ПA ijk 12
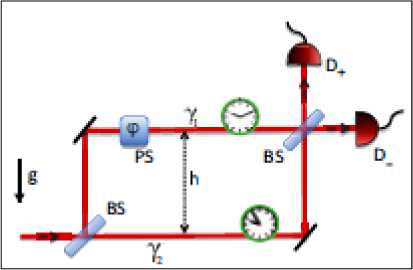
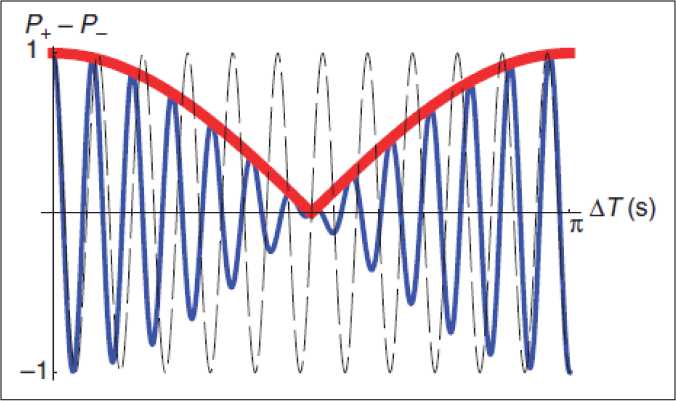
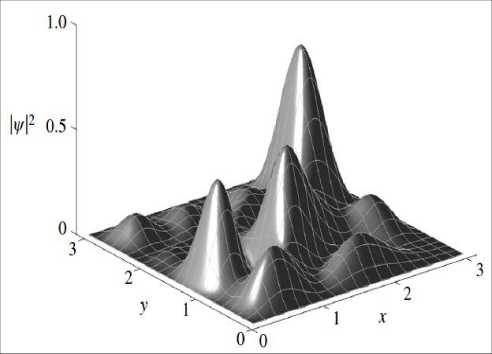
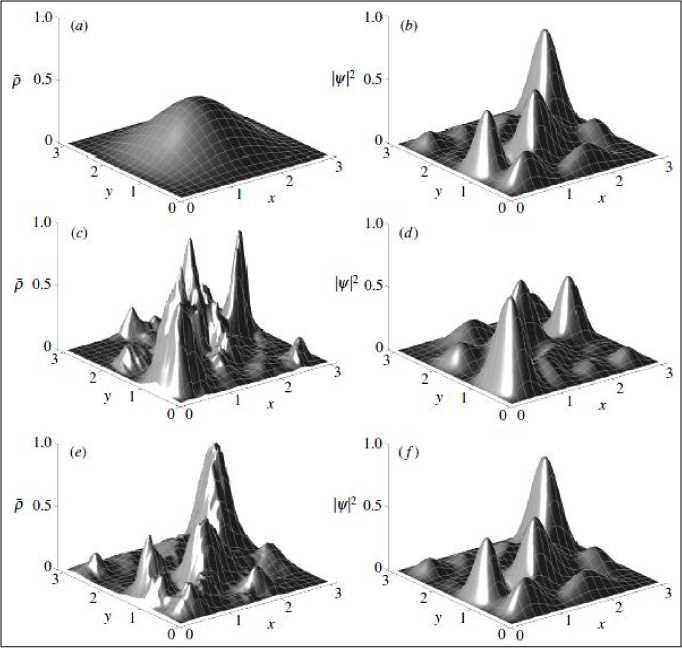
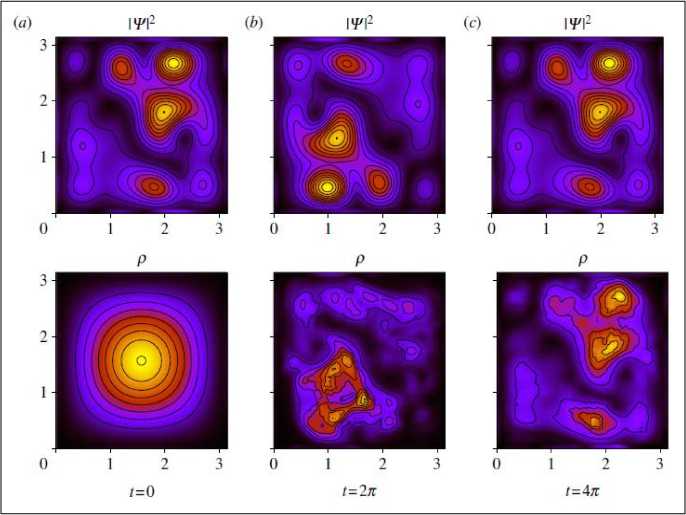
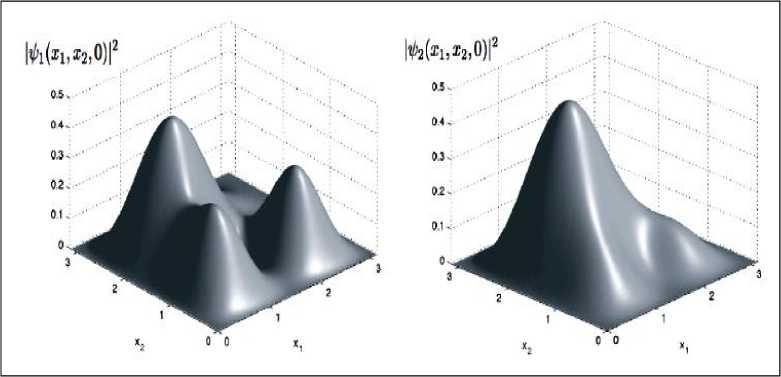
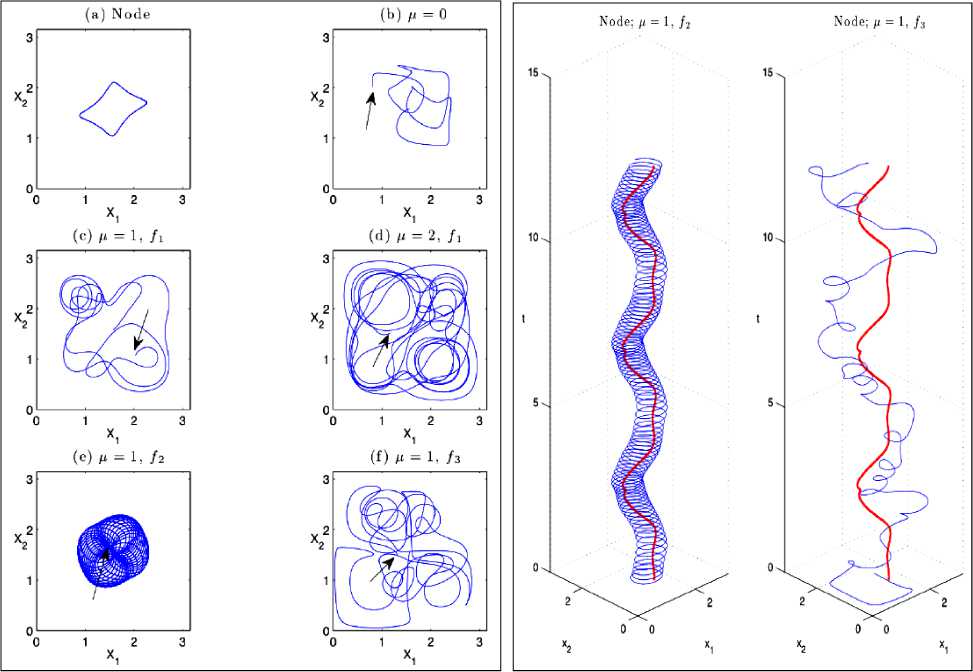
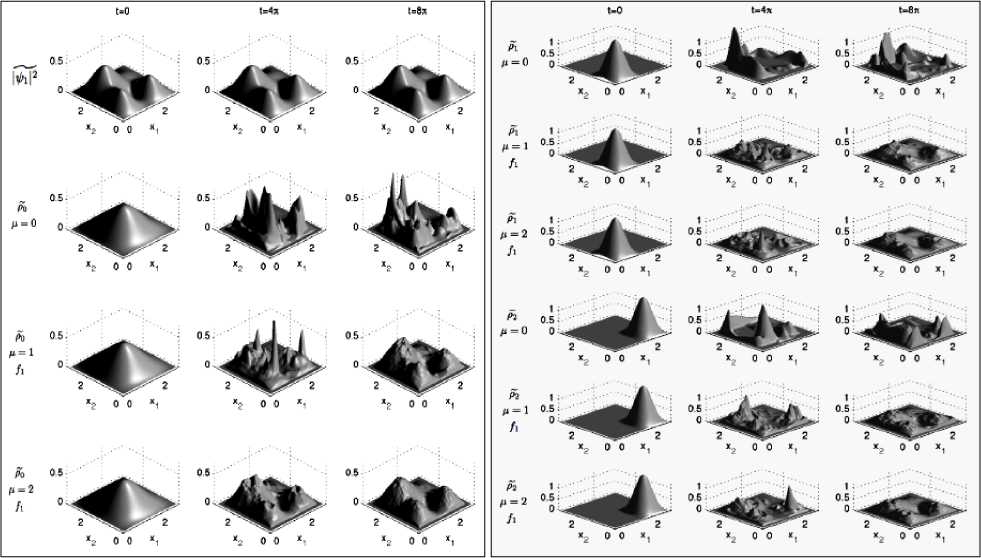
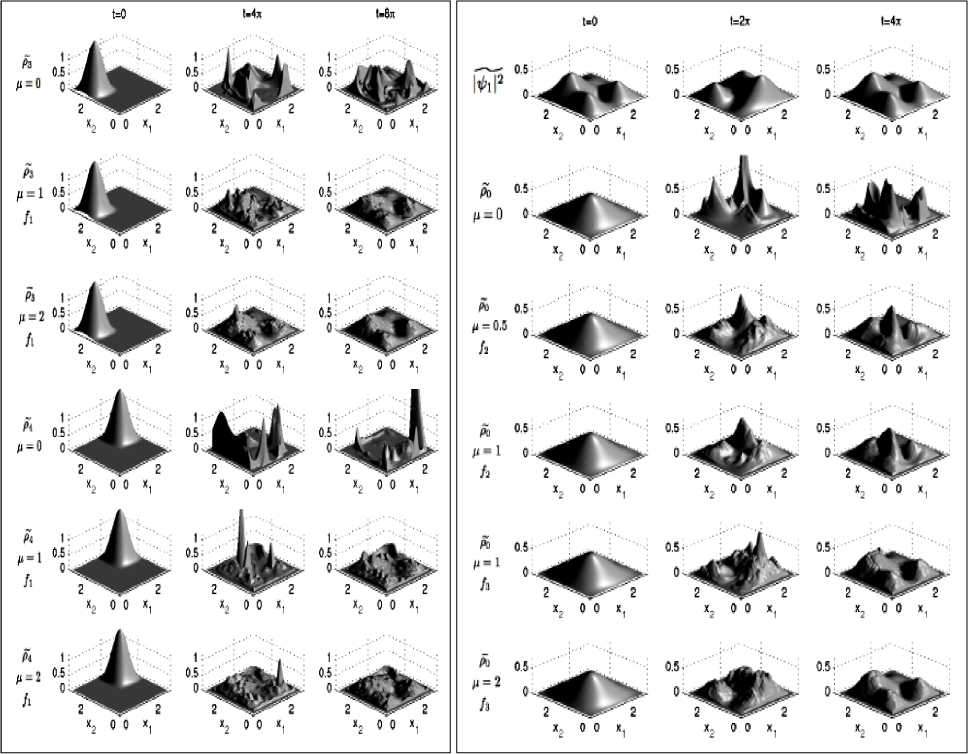
i Тогда из (1) и (2) следует25, что PA A...и AN N Ai i1 и фазы ф задаются в виде: фi cos 1 P A1 и A2и...иAi1 Ai 2 P A1 и A2 и...иAi1 Ai + ^1,2, .,i 1 , а величина ф вычисляется из выражения wAиA и...иAi1 1,2, ,i1 ej 1,2, ,i 1 Из (3) для бинарных событий A, A вероятность: PAиA = 1^ AwA2 2A1 2A2+2^A •^ A cos ф >2 -у1 (5) и означает интерференцию вероятностей. Допустим, что имеются два бинарных случайных события A00,A11 временного ряда представленного двумя комплексными волновыми функциями ^A и^ A1 . Обозначим для простоты ^A00 и^ A1 1. Рассмотрим принцип допол нительности на временной последовательности, состоящей из бинарных состояний. - Принцип дополнительности Определим дискретное преобразование Фурье (ДПФ) как N1jik2N1jik2 X x e N, x X e N. Вероятность P A0 0 0 0 , P A1 1 1 1 , в x – i0k0 представлении, согласно (1). Определим ДПФ волновых функций W0, 1как V0, 1в виде: Vk0 ie0= ф01 иVk1 iejiл = ф01.(6) i0 В k -представлении вероятность можно определить как Pk 0 = у/k0•у/*k0= 1^22+2 Vn 0 •ф cos ф ,(7) Pk 1 = фk1•фk1= \ф 2 2 2 \ф0 •ф cos ф ,(8) где ф означает фазу отличия двух комплексных чисел Wиф . Обратные ДПФ вероятностей (7) и (8) описывают связь между двумя последовательными квантовыми объектами. - Запутанные состояния (entanglement). Допустим, что два события A и A +определены волновыми функциями фиф . Определим вероятности PA 0 A + 11=\ф012 2\ф0• ф1 cos ф, где ф означает фазу отличия двух комплексных чисел фиф . Тогда, согласно выше введенным определениям P A 0 A + 1 0 . Это условие определяется из (4) для значения ф в виде: ср = а cos . ф01 Если, например, положить, что ^011/2, то ф = л и получим запутанное состояние. Полученное запутанное состояние имеет свойство P At1 At+ 1 0 1 . Можно также изна- чально место исходного условия P At0 At + 1 1 0 принять условие, что P At1 At1 0 0 .(11) Тогда запутанное состояние приводит к следующему результату: P At0 At1 1 1 .(12) Условия (11) и (12) можно записать в обозначениях Дирака «бра-кэт» как 1 0 1 1 0 101 10 .(13) Выражение (13) называется запутанным состоянием Бэлла. Физической особенностью состояния (13) заключается в том, что, измерение в первом объекте (вероятность измерения 0 равна ½ и вероятность измерения 1 также равна ½) полностью определяет результат независимо проводимого измерения над вторым объектом, что невозможно в классическом случае. Такой эффект отсутствует в классической физике и отражает глубокое отличие логики квантовой механики от классической логики интерпретации результатов измерения (отсутствие влияния результатов измерения и их независимость). Пример 3: Гравитационные эффекты общей теории относительности и квантовая интерференция фотонов. Одним из перспективных физических экспериментов проверки влияния гравитации на квантовую систему является интерференционные измерения изменения фазы движения квантовой частицы (фотона) в гравитационном потенциале. Данные результаты имеют важное значение для разработки квантовой метрологии и теории измерений. Типовым примером является эксперимент с интерферометром типа Маха-Цендера (рис. 7) в гравитационном поле Земли, где частица (фотон) движется в когерентной суперпозиции вдоль двух путей интерферометра , , которые имеют собственные длины и разделены на расстояние h . (а) (б) Рис. 7. Интеферометр Маха-Цендера (а) и эксперимент с интерферометром Франсона для тестирования локального реального описания гравитационного замедления времени при движении фотонов в гравитационном потенциале (б) Две амплитуды в суперпозиции имеют разные, зависимые от траектории, фазы ,i 1,2 . Дополнительно частица имеет контролируемый относительный сдвиг по фазе . Принимая во внимание действие первого разделителя луча и обозначая через rj моду, ассоциированную с соответствующим путем , состояние МЗ интерферометра Маха-Цендера можно представить как МЗ 1 ie i 1r1e i 2i r2. Тогда частица обнаруживается одним из детекторов D с соответствующей вероятностью P как P cos , где . Фаза пропорциональна действию вдоль соответствующий (полуклассической) траектории у , по которой движется частица. Для свободной частицы в соответствующей метрике пространства – времени действие выражается через собственное время T в виде S mc2 dT . Это означает, что измерение величины АФ может демонстрировать i J/ i экспериментально обобщенную релятивистскую задержку времени. Рассмотрим теперь предыдущую ситуацию, когда частица в суперпозиционном состоянии имеет внутреннюю степень свободы, которая выражена в учете собственного времени в виде часов (рис. 8), которое отлично для разных путей движения частицы в гравитационном потенциале. Рис. 8. Интеферометр Маха-Зендера для измерения эффекта общей теории относительности замедления времени на волновой функции простой квантовой системы Обозначим через r i соответствующее состояние часов с соответствующим собственным временем для траектории у . Тогда суперпозиция состояния интерферометра будет иметь вид запутанного состояния: Согласно общей теории относительности, время не является абсолютной величиной и зависит от геометрии пространства-времени. Это означает, что часы находятся в разных квантовых состояниях, зависящие от траектории движения. Уравнение (14), согласно квантовой механике описывает запутанное состояние, и интерференция зависит от степени свободы одного из состояний часов траектории движения фотона. Тогда измерение степени свободы приводит к успешному извлечению искомой информации (which-way information). Частный след по состоянию часов в (14) приводит в определению вероятностей P , ассоциированных с детекторами D в виде: где V 1 2 1 2 ei и АФ = Ф . Если варьировать дополнительный сдвиг фазы Ф , то веро ятности P осциллируют с амплитудой V , которая называется прозрачностью интерференции обра-max Pmin зов. Формально V =---Ф-------Ф— и для случая (15) имеет вид: max Pmin ф ±Ф ± V = |(r12 Прозрачность интерференции образов зависит от различимости состояний часов, которые движутся по разным траекториям интерферометра. Если через D обозначить количество информации, извлекаемое из траектории движения часов (различимость траекторий) как вероятность правильного угадывания пути движения часов, то D = ^1 —|^ |т2)| . Принцип дополнительности можно выразить в виде хорошо известного соотношения дуальности D2+ V2= 1. Рассмотрим теперь на конкретном примере взаимосвязь общей теории относительности и квантовой механики. Массивные квантовые «часы» во внешнем гравитационном поле. Допустим, что степени свободы квантовых «часов» соответствуют внутренним состояниям массивной частицы и Гамильтониан H описывает внутреннюю эволюцию частицы. В неподвижной системе отсчета координате времени соответствует собственное время и эволюция внутренних состояний частицы описывается уравнением вида ih /1 Вт нН. Изменения координат в лабораторной системе отсчета приводит к уравнению ih В / tt = нН, где t = dT / dt и показывает как быстро собственное время изменяется по отношению к координатному времени. Для обобщенной метрики пространства времени g данное изменение описывается как g x x , где используется сигнатура подразумевается суммирование по индексам. Тензор момента – энергии массивной частицы можно определить через функциональную производную как T^v s 5S / 5gиv . Так как энергия частицы E определяется как компонента тензора То в виде E = g0цg0рТцv. В этом случае для свободной эволюции в пространстве-времени со стационарной метрикой (в системе координат, в которой gQj = 0 для j = 1,2,3) имеем E = mc2 . g00 , gxx где m означает массу частицы. Вблизи поверхности Земли геометрия пространства-времени описывается метрикой Шварцшильда. В изотропных координатах x,0,9 и Q2 = d02+sin20d92 имеем c2 dr2 1 + Ц 2 c c A 4 1-. 2 c c 4 c2dt2 2 c2 dx2 + x2dfi2 , где X x = —MM / x означает гравитационный потенциал Земли (G - гравитационная постоянная и M – масса Земли). После аппроксимации в предположении о слабом гравитационном поле и медленном движении частицы в поле и удаления малых квадратичных членов в кинетической и потенциальных энергиях получим компоненты метрики в виде: , =-fl + 2 ^x) + 2^x)2) „ е f1 3Ф(x Л , gii=6iA 1-2^" , c g 00 1 T 2 4 cc в Нлаб mc2 H EkГр (2x)(mc2 H EкГоррр), где EkГр p 1 3 c 2m p 2mc 12H mc 1 p2 и E Гр m (x) 3 . Согласно рис. 8, частица движется в состоянии суперпозиции по двум рр 2 2m фиксированным не геодезическим путям , в однородном гравитационном поле. Ускорение и замедление, с которым движется частица вдоль направления x , предполагается одинаковыми для обеих траекторий, также как постоянная скорость вдоль оси y . Это означает, что траектории имеют различную собственную длину и только специальные релятивистские эффекты влияют на замедление времени. МЗ Состояние частицы внутри интерферометра описывается суперпозицией i1ei 2, гдесостояниям i соответствуют две траектории движения , которые задаются Гамильтонианом Н с начальными значениями, которые обозначим как xнач нач . С точностью до обобщенной фазы эти состояния определяются интегралом путей i dt(x)mc2H EкГоррр Фейнмана в виде: |^/^ = eй*' c lxиач\к.нач\. При малых размерах интерферометра, центральный гравитационный потенциал x можно аппроксимировать линейной формой на расстоянии h между двумя траекториями в виде: R h R g h O h2 , где g GM / R2 означает значение ускорения в гравитационном поле Земли в исходной лабораторной системе отсчета, которая удалена от центра Земли на расстояние R . Для частицы, имеющей два внутренних состояния с соответствующими энергиями E, E, Гамильтониан в системе покоя для внутренних степеней свободы можно записать как H E00 0 E11 1 , и выберем начальные условия для данных степеней свободы в виде квантовой суперпозиции: нач 0 1. Тогда вероятности обнаружения частицы определяется26 в следующем виде: 1 1 EVT P , m, E, V , T cos cos 2 2< 2й c ) 1 VT Й c2 где T – время (измеряемое в лабораторной системе отсчета) движения частицы в интерферометре состояния суперпозиции по двум траекториям, V g h определяет разницу гравитационного Гр Гр потенциала между траекториями, E корр определяет коррекцию Eкорр , усредненную по двум траекториям и E E E . Усредненное значение H осуществляется в соответствии с начальными условиями нач . Соответствующее значение прозрачности (16) определяется как V cos EVT 2 c2 . Отметим следующий важный факт. Введение степеней свободы квантовых «часов» дает два новых квантовых эффекта, которые не могут быть получены без введения общей теории относительности в квантовую механику: изменение прозрачности интерферометра и сдвиг фазы пропорционально внутренней энергии, согласно определению величины P- ф, m, E, АV, АT (рис. 9). Пунктиром черного цвета обозначено выражение вероятности без квантовых часов. При введении часов (синяя линия) получаем два эффекта: изменение величины прозрачности интерферометра задается абсолютным значением первого косинуса (красная линия) и фазовый сдвиг пропорциональный усредненной внутренней энергии «часов». Сдвиг фазы означает, что изменение обобщенного релятивистского собственного время неизбежно приводит к снижению прозрачности. Изменение прозрачности является следствием прямого взаимодействия внутренних степеней свободы частицы, влияющего на эффективный потенциал обобщенного Гамильтониана Н . Рис. 9. Прозрачность интерференционных образов и сдвиг фазы в случае с/без квантовых часов Такой эффект полностью отсутствует в ньютоновой модели гравитации, что отражает возможность математически предсказать изменение хода часов при движении в различных гравитационных потенциалов проверить нарушение неравенства Белла. Это взаимодействие полностью согласуется с принципом эквивалентности Эйнштейна27. Рассмотрим теперь кратко частный случай метрики (18), важный для оценки чувствительного физического эксперимента к изменению модели пространственно-временного континуума. – Чувствительность к малым параметрам метрики инерциальной системы отсчета. Отметим некоторые особенности инерциальных систем отсчета в ОТО (подробное описание дано ниже). Известно, что в гравитационном поле не может быть введена глобальная система отсчета [27]. В этом поле (в отличии от электромагнитного поля) могут быть введены только локальные инерциальные системы отсчета, которые ускоренно движутся друг относительно друга, если только расстояние между ними бесконечно мало. Таким образом, в гравитационном поле имеет место только локальная лоренц-инвариантность [27]. Вопрос выбора и конструирования систем отсчета рассмотрим ниже. Здесь следует обратить внимание на то существенное обстоятельство, что локальная система координат в гравитационном поле может быть реализована в виде достаточно малой по размеру системы координат, жестко связанной с небольшим размером, свободно падающим в этом поле телом (например, со спутником), при условии, что это тело не совершает вращательного движения. Следует также подчеркнуть (и это очень существенно), что в такой локальной инерциальной системе координат ось времени должна быть ортогональна пространственной координатной гиперповерхности этой системы координат28. В 1956 г. Уитияма, исходя из локальной лоренц-инвариантности в гравитационном поле (т.е. в зависимости параметров группы Лоренца от криволинейных координат) показал, что необходимым следствием этого обстоятельства является кривизна пространства-времени. Свободно падающая в гравитационном поле достаточно малой массы частица движется по геодезической линии искривленного 4-мерного пространственно-временного континуума. Здесь имеет место полная аналогия с классической механикой Ньютона, согласно которой материальная точка, находящаяся на поверхности, будет в результате начального импульса двигаться по геодезической этой поверхности (в случае отсутствия каких-либо других внешних сил). Так планеты, движущиеся по своим орбитам вокруг Солнца, по существу, движутся по инерции, т.е. свободно падают в искривленном 4-мерном континууме. Возникает вопрос: почему при очень тщательных измерениях положения планет в солнечной системе никаких отклонений от евклидова характера 3-мерного пространства не было обнаружено? Дело в том, что основная метрическая форма псевдоевклидова пространства (т.е. в отсутствии гравитации) имеет вид: ds2c2dt2dx12dx22dx32 . (19) Поскольку пространственно подобная гиперплоскость в пределах солнечной системы должна носить (с большим приближением) евклидовый характер, то основную метрическую форму пространственно-временного континуума в указанной области можно представить только в виде: ds2c2 1 dt2 dx12 + dx22 + dx32 , 2ф причем -«1. Физически последнее ограничение означает, что возможные отклонения от c2 псевдоевклидова пространственно-временного континуума в пределах солнечной системы должны быть очень малыми величинами. В поле слабого потенциала тяготения ф , описываемого метрикой (1.20), материальная точка достаточно малой массы движется по геодезической пространственновременного континуума, т.е. для действительной траектории должна обращаться в нуль первая вариация интеграла s1 5 j ds 0 . s0 Учитывая выражение (1.20), можно уравнение (21) записать в виде: Здесь v2 1>2 dx1 dt s1 ^ J ds = 3c s0 2>2 dx2 dt 3л2 dx3 dt dx1 2dx2 2dx32 c2dt2 – скорость движения материальной точки. 2ф Учитывая, что -«1, можно записать: ф c2 Подставив это разложение в интеграл (22), получим Итак, в первом приближении закон движения материальной точки по геодезической пространственно-временного континуума сводится к принципу Гамильтона-Остроградского, если только рассматривать функцию ф как потенциал поля тяготения в его ньютоновском смысле. Приняв эту интерпретацию функции ф , можно в качестве второго приближения принять уравнение (22). Исходя из (22) получим следующее уравнение движения материальной точки: dmvm m grad , m dt v2 2 c2c2 где m – масса покоя материальной частицы. Уравнения (25) были получены Т. Леви-Чивита. Итак, несмотря на весьма малые отклонения от псевдоевклидова характера пространственновременного континуума, геодезические в этом пространстве испытывают существенные изменения, их проекции на пространственно-подобные гиперповерхности (т.е. на 3-мерное пространство) превращается вместо прямых линий в эллипсы или гиперболы. Следовательно, поток геодезических в псевдоевклидовом пространстве весьма чувствителен к малым отклонениям от псевдоевклидовости, что необходимо учитывать в проведении физических экспериментов на искусственных спутниках Земли. В этой своеобразной неустойчивости заключается физическая особенность модели гравитационного поля; в евклидовых или римановых пространствах с положительно определенной метрической квадратичной формой данный факт не имеет место. Следует отметить, что сам принцип Гамильтона-Остроградского является, в сущности, принципом геодезической для слабых гравитационных полей. Таким образом, разработка наукоёмких ИТ затрагивает одновременно пересмотр исходных положений таких фундаментальных теорий как квантовая механика, общая теория квантовой гравитации, квантовой релятивистской термодинамики, теории неразрушающих квантовых измерений в криволинейном пространстве-времени, квантовой релятивистской теории описания поведения релятивистской частицы в римановом и неримановом пространственно – временном континууме и мн. др. В свою очередь, существование алгоритмической неразрешимости при применении традиционных вычислительных методов и количественных подходов к поиску оптимальных решений сложных задач физики, механики, биофизики, систем управления, развитие наукоемких компьютерных (типа квантового компьютера) и прорывных ИТ типа квантовый Интернет на основе квантовых слепых облачных вычислений (quantum blind cloud computing), квантовая криптография, квантового управления наноструктурами, формирования интеллектуальных наноматериалов, разработка ИТ нанотехнологий и мн. др. привело к необходимости поиска и развития технологий на основе новых видов интеллектуальных вычислений (ИВ) и программно-аппаратной поддержки вычислительных процессов. Разработка подобных наукоёмких платформ элементной базы аппаратной поддержки квантовых ИТ потребовало одновременно создания и внедрения новых видов нанотехнологий изготовления материалов и технологической оснастки. Резко возросший объем перерабатываемой информации и сложность решаемых задач в науке и технике привел к необходимости создания новой элементной 22 базы квантового компьютера, способного реализовать квантовый массивный параллелизм обработки информации, решать классические алгоритмически неразрешимые задачи с экспоненциальной скоростью, обладая огромной памятью и быстродействием. Поэтому выбранное решение фундаментальных и прикладных проблем конкретной технологии ИВ существенно влияет на эффективность разработки и качество применения моделей наукоемких ИТ. Возрастание сложности структур современных физических объектов и логических устройств, трудности прогнозирования непредвиденных (нештатных) ситуаций управления только усиливают актуальность данной проблемы и внимание к поиску её решения. Такого рода задачи относятся к т.н. проблеме «Intelligent System of Systems Engineering». В указанной проблеме изучаются в общем виде сложные структуры систем управления с различными уровнями и шкалами интеграции и/или приоритетным обменом информации между подсистемами с целью установления необходимых и достаточных условий надёжного автономного функционирования объекта управления (ОУ) во внешней среде. В теории и систем управления одним из эффективных подходов снижения риска принятия решения (от неполноты описания модели ОУ) является разработка структур робастных ИСУ. Данные структуры реализуют принцип компенсации неопределенности описания модели ОУ за счет повышения уровня интеллектуальности традиционных систем управления. В частности, компенсация информационной неопределенности осуществляется за счет повышения интеллектуальности нижнего исполнительского уровня в виде соответствующих структур интеллектуальных регуляторов и соответственно спроектированных (с учетом в продукционных правилах информационного риска) самоорганизующихся робастных баз знаний (БЗ). Таким образом, реализация данного принципа обеспечивает робастность ИСУ при неполном описании модели ОУ за счет учета в продукционных правилах проектируемых БЗ неточной (imperfect), извлекаемой из данной модели, информации и самоорганизации БЗ. Выбор корректной модели, в первую очередь ОУ минимальной алгоритмической сложности, является важной для практики задачей. Однако сам критерий минимальной алгоритмической сложности при выборе метода описания модели ОУ требует уточнения и физического обоснования. Данный вывод усиливается при исследовании моделей квантовых и релятивистских ОУ в разработке квантовой информатики, систем квантового и релятивистского управления наноструктурами, нанотехнологий проектирования интеллектуальных материалов и др. В результате реализация отмеченного принципа осуществляется выбором соответствующего уровня ИВ и является одним из основных положений при разработке новых видов ИВ. Построение новых моделей квантовой информатики и квантового релятивистского управления для корректной интерпретации требуют привлечения методов нестандартных (квантовой и релятивистской) логик, обладают многими «парадоксами» логического вывода и суждений и связаны с решением т.н. проблемы Вундгейлера корректного описания моделей. Целью данной работы является разъяснение (по возможности подробное) особенностей квантовой механики, как основы квантовой информатики, и роль ее решения в построении корректных моделей описания и проектирования физических объектов, представленных на рис. 3-8 в задачах обработки массивов информации и интеллектуального управления. Физические особенности применения квантовых и релятивистских эффектов в моделях интеллектуальных вычислений На необходимость перехода от традиционных методов к новым инновационным технологиям доступного изложения основ квантовой механики для системной инженерии указывалось неоднократно29,30 [2-24]. Ранее была рассмотрена математическая модель квантового постулата, предложенного в [27-29] на основе модифицированного волнового уравнения Гамильтона-Якоби и его характеристического многообразия. Такой подход позволяет объединить волновые уравнения квантовой механики в единую систему и перенести методы классической теории управления и алгоритмов на квантовую область. Обсуждение физической интерпретации основных квантовых операторов, структур квантовых алгоритмов, их взаимоотношений и свойств, часто используемых в решении задач компьютерных нанотехнологий и вычислительных процессов, ИТ, глобальной оптимизации и в процессах проектирования робастных интеллектуальных систем управления (ИСУ), основано на свойствах решений уравнений Шрёдингера, Фока-Клейна-Гордона и Дирака. Применение результатов интерпретации решений соответствующих волновых уравнений квантовой механики позволяет дать корректную физическую интерпретацию вводимых понятий и определений в инженерии компьютерных ИТ и нанотехнологий. Необходимость перехода от традиционных методов к новым инновационным технологиям доступного изложения основ квантовой механики связана также с фактом, что существовал психологический барьер восприятия широкой инженерной аудиторией математического аппарата квантовой механики, «парадоксов» выводов квантовой логики [30-33] и решений, получаемых на основе квантовых алгоритмов [34-36]. Поэтому для разработки прикладных моделей новых видов интеллектуальных вычислений и их эффективного применения в прикладных задачах управления возникла необходимость более детального и доступного изложения основ квантовой механики, используемых, например, в теории квантовых вычислений и квантовых алгоритмов. В частности, в настоящее время слабое внимание данному вопросу уделяется при подготовке бакалавров, магистров и инженеров-исследователей в области компьютерных технологий, ИСУ и принятия решений, робототехники и мехатроники. В результате, к настоящему времени возник определенный разрыв в университетских программах и методологии учебных процессов при освещении вопросов физических аспектов и структурной реализации квантовых вычислений и квантовых алгоритмов на доступном (для широкого круга инженерных специальностей) уровне. Более того, вопросы обучения в области квантовых вычислений и квантовых алгоритмов в основном рассматриваются для физико-математического образования31, игнорируя потребности инженерной аудитории. Так, например в области оптимального проектирования современных элементов и средств ЭВМ32 или проектирования ИСУ33 методы квантовых вычислений показали высокую эффективность решения многих задач. В данном разделе отражен также важный (и необходимый для практики) методологический аспект подробного описания (и доступного для специалистов в области теории и систем управления) физических и математических основ аксиоматики квантовой релятивистской механики, используемых в моделях интеллектуальных квантовых мягких вычислений, а также для проектирования робастных ИСУ в непредвиденных ситуациях управления. Необходимость данного описания объясняется во многом трудностями восприятия квантовых и релятивистских эффектов, результатов квантовой теории информации и возникающих при физической интерпретации логических «парадоксов», противоречащих выводам классической Булевой логики. Так, например, трудности для интерпретации вызывает экспериментально установленное явление дефекта массы как релятивистского эффекта (две сталкивающиеся частицы малой массы и ограниченной энергии в неподвижной системе отсчета (системе покоя) выделяют энергию, на порядки превосходящую сумму энергий подсистем, – явление взрыва атомной бомбы). Другим примером является трудность разъяснения самоорганизации запутанных состояний (две подсистемы, находящиеся в хаотическом смешанном состоянии с максимальными энтропиями, образуют чистое состояние с нулевой энтропией) как квантового синергетического эффекта теории информации. Оба данных эффекта, разных по своей физической природе, для корректной интерпретации требуют привлечения новых понятий, таких как синергетический эффект. Например, новый информационный синергетический эффект самоорганизации знаний заключается в приобретении системой требуемого свойства робастности за счет информационного (а не прямого физического) взаимодействия не робастных БЗ, т.е. появления нового качества в объединенной системе, отсутствующего во взаимодействующих подсистемах, составляющих единую систему34. При этом подчеркнем еще раз, подсистемы не содержат нового качества (робастности), содержащегося в составной системе и сформированного из качеств данных подсистем (не робастности). Данный эффект реализуется процессом обмена и переноса скрытой в классических состояниях квантовой информации и является следствием формирования виртуальных каналов передачи квантовой информации между классическими состояниями сигналов управления. Неклассические физические свойства нелокальности суперпозиции с квантовой корреляцией между подсистемами как математического объекта приводят к парадоксу нарушения элементарного арифметического правила35 в виде: 2 ^1+ 1 . Информационный анализ неопределенности в состоянии составной квантовой системы позволяет четко разъяснить наличие необычных (неклассических) свойств: игнорирование в ней части информации о состоянии подсистемы приводит к увеличению квантовой неопределённости. В результате, имеем следующий факт36,37: при определенных условиях возможно, что в «части» (подсистеме) количества квантовой неопределенности может быть больше, чем в «полной» (составной) квантовой системе. Такой эффект отсутствует в классических системах в силу свойств и определения классической меры информационной энтропии Шеннона. С точки зрения логики корректной интерпретации физических явлений, проблема заключается в том, что классическая Булева логика не может объяснить формирование нового качества в единой системе, не содержащегося в составных подсистемах. Отметим, что корректное объяснение средствами квантовой нечеткой логики достигается за счет отказа от аксиомы дистрибутивности классической логики или от закона исключения третьего (в нечеткой логике). При этом традиционно используется основной тезис фон Неймана: «Квантовым уравнениям, описывающим движение квантовой частицы, может быть сопоставлена адекватная логическая система». Расширенный (уточненный) вариант этого тезиса можно сформулировать следующим образом: физическое явление, имеющее пространственновременную динамику, может быть описано как в рамках динамических уравнений движения, так и адекватно в виде логико-динамической системы (на уровне логики причинно-следственных связей). В дальнейших исследованиях было установлено, что квантовая логическая система интерпретации результатов физических наблюдений и измерений существенно отличается от аналогов классической логики. Так в трехзначной квантовой логике используется третье значение истинности (неопределенный). Поскольку оба дизъюнкта истинной дизъюнкции могут быть ложными, здесь возникает асимметрия между дизъюнкцией и конъюнкцией, т.е. законы дистрибутивности в общем случае не выполняются. Накопленный педагогический опыт (за период 1972-2012гг.) чтения лекций по теории относительности, квантовой механике, термодинамике, мягким и квантовым вычислениям (в области интеллектуальной робототехники и высоких ИТ проектирования ИСУ для нанотехнологий и квантового управления) и его анализ показал также следующее. Трудности изучения и особенно применения квантовых вычислений специалистами в области системной инженерии, компьютерных технологий, вычислительных процессов и в теории и систем управления носят часто психологический и инерционный когнитивный характер ассоциативного (порой негативного) восприятия идей и принципов квантовой механики или теории относительности. Эти трудности вызваны попытками применения механических аналогий восприятия и интерпретации квантовых явлений из классической физики38. Так происходит до сих пор, например, при попытках студентами интерпретации квантового эффекта туннелирования [32, 33], которые постоянно прибегают к механическим аналогиям. Отказ от привычных аналогий носит порой драматичный характер39. Данные факты объясняются, с другой стороны, многообразием моделей самой квантовой механики [22, 34, 35, 37, 38]. К настоящему времени вопрос о полноте доказательности корректности той или иной модели квантовой механики остается открытым [22, 37] из-за существования ряда «парадоксов» и их неоднозначности в интерпретации [34, 35, 38]. Более того, в отечественной и зарубежной литературе отсутствуют проблемно-ориентированные методологические учебные пособия (см., например, дискуссию в [30, 31]) с конкретными наглядными инженерными приложениями, иллюстрирующих их практическую эффективность, например, для решения задач теории и проектирования систем управления. Все перечисленное40,41 и ряд других42 методологических трудностей, приводят к необходимости разработки эффективной теории квантового интеллектуального управления ОУ в макро-, микро- и нанотехнологиях [29, 39, 40, 41]. Рассмотрим предварительно некоторые из перечисленных выше вопросов квантовой механики. Пример 4: Вывод уравнения фон Неймана из уравнения Шредингера Рассмотрим вывод одного важного для квантовой теории информации и теории квантовых алгоритмов уравнения фон Неймана для оператора плотности р=ИИ квантового состояния из уравнения Шредингера, описывающего эволюцию квантового состояния 1^ . В общем виде оператор плотности может быть записан как внешнее произведение векторов состояния, т.е. /9 = pW . k Для кет- и бра- векторов W и ^1 имеем уравнения Шредингера в виде: dк)=_iH и кк i H, dt й dt где использовано свойство эрмитовости Гамильтониана H . Тогда производная от оператора плотности будет иметь вид: dd1^tdt It■р t =2k kkk . dt kdt Используя значения производных от векторов квантовых состояний, получим d■р t i pkH VktwktI-Z pk кkt)(^ ktIH[ dt k k Правую часть приведенного выражения можно представить через коммутатор A, B в виде: AB BA квантовой ^ q,t (в dti H, t. dtй Уравнение (26) называется уравнением фон Неймана для оператора плотности. Пример 5: Динамические основы квантовой вероятности и постулат Борна. В механике предполагается, что ансамбль систем, описываемый волновой функцией конфигурационном пространстве) обладает конфигурацией q , распределенной по правилу вероятности состояния Борна в виде р q,t q,t I , а волновая функция описывает амплитуду вероятностей. Более точно, предполагается, что р q,0 q,0 I в начальный момент времени t 0 и уравнения движения затем гарантируют, что данное вероятностное распределение сохраняется во все последующие времена. В большинстве моделей квантовой (детерминистской) механики выражение p=V\2 принимается в качестве аксимы, и поэтому предположение, что ансамбль в начальном состоянии t 0 с волновой функцией ^ q ,0 будет иметь р q, 0 q, 0 I на пространстве конфигурации q . Рассмотрим данный вопрос с точки зрения динамического поведения квантовой системы (26) в двумерном пространстве. Допустим, что частица единичной массой движется в двумерном пространстве в потенциальном поле V . Система имеет конфигурацию q x, y и волновую функцию ^ = ^ x,y ,t (предполагается чистое состояние). Волновая функция ^ q,t , которая удовлетворяет решению уравнения Шрёдингера в виде й =1: t 2x22y2V. В моделе Луи де Бройля-Бома движение частицы следует по траектории x t , y t определяется через волновую функцию ^ q, t согласно закону соответствия де Бройля: dxIm ^ = vS, dt ^ где ^ = и exp iS . Математически член ImVy/ / у/ определяет отношение потока квантовой вероятности к плотности квантовой вероятности. Физически, однако, волновая функция у/ интерпретируется как объек- тивное поле (в конфигурационном пространстве), определяющим движение простой частицы. При этом уравнения (27) и (28) определяют детерминированное поведение частицы и не содержат информации о вероятности поведения ансамбля. Задавая начальные условия волновой функции ^ x, у, 0 решение уравнения (27) определяет поведение волновой функции ip x, у, t на все отрезки времени; задавая начальные условия позиции частицы x 0 , у 0 , решение уравнения (28) определяет поведение траектории x t , у t на все отрезки времени. Для ансамбля независимых частиц, каждая из которых описывется одинаковой волновой функцией ip x, у, t , можно определить плотность р x, у, t для реальной конфигурации x t , у t в момент времени t. Решение уравнения (28) определяет поле скоростей x t , у t и для ансамбля частиц с одинаковой волновой функцией ip поле x t , у t определяет эволюцию распределения р x, у, t согласно уравнению непрерывности: xy . txy Так как уравнение (27) включает в себя уравнение непрерывности аЫ2 5 И2 x 5 Id2 у ^^+----+=о txy для |у/|2, то частное начальное условие р x,у,0 = ^р x,у,0 | переходит в течении времени в состояние р x,у,t =^/ x,у,t | . Состояние «квантовое равновесие» обеспечивается динамическим поведением квантовой системы. Отметим, что (29) определяет эволюцию некоторого начального распределения Р x, у,0 , которое может быть Р x, у,0 # \у x, у,0 |2. Задавая У x, у,0 , уравнение (27) определяет эволюцию ip x, у, t на все остальные отрезки времени, а (28) задает поле скоростей x, у также на все остальные отрезки времени. При известном поле скоростей x, у (29) можно проинтегрировать и определить плотность р x, у, t для всех t для всех р x, у,0 . Примечание 3. Прежде чем проводить анализ дальше, остановимся еще раз на сравнении изложенного выше с аналогом эволюции классической системы с заданным Гамильтонианом на фазовом пространстве. В классической механике траектория q t , pt в фазовом пространстве индивиду- HH альной системы определяется уравнениями Гамильтона в виде q =---, p —--при заданных pq начальных условиях q0, p0 . Эти уравнения определяют поле скоростей q, p , которое определяет эволюцию некоторого распределения р q, p, t как решение уравнения непрерывности qp --1---1--= 0, которое можно переписать как--1- р, H = 0 и является аналогом tx y t Рассмотрим аналогичный пример для частиц в двумерном ящике с простым начальном распределением р x, у,0 ^ |у/ x, у,0 |2 (слабо структурированный ансамбль). Отметим предварительно, что из численного интегрирования (29), что распределение ансамбля стремится к распределению равновесия м2 (структурированный ансамбль). Допустим, что частица находится в квадратном ящике размером 71 с бесконечными барьерами на границах x, y 0, Л . Для оператора энергии собственные функции определяются как 2 122 mn x, y sin mx sin ny с собственными значениями E m + n , где 71 mn2 m, n 1,2,3, являются положительными величинами. В качестве конкретного примера рассмотрим начальную волновую функцию ^ x, y,0 и t 0 как суперпозицию первых 16 мод, m, n 1,2,3,4 с эквивалентными по модулю амплитудами, но со случайно выбранными фазами : V x, y, 0 mn x, y exp i6mn . m.n 1 График квадрата амплитуды у x, y,0 представлен на рис. 10. Рис. 10. Вид квадрата амплитуды 1^ x, y,0 для суперпозиции первых 16 мод двумерного ящика Из уравнения Шрёдингера (27) вид волновой функции определяется как: x, y,t mn x, y exp [ i6 mn Emnt ] . (32) 4 m,n 1 Отметим, что волновая функция у/ является периодической во времени с периодом 4л , так как член 4ЛE имеет всегда целочисленный множитель 2 Л. Из (28) определяются компоненты скоростей частицы как: dx i ОШ ^ОШ dy i ОШ *0Ш --=---5- ^——^ — и ■ =---5",// -. 'И „ dt 2 и2 x Сx dt 2 м2y y Построение точного распределения для структурированных систем является сложной задачей и используется метод разбиения на ячейки размером £Г . Распреление Р усредняется по данным ячей- 12 - f dxdyр. ячейка кам относительно ее координат центра согласно выражению Результат усреднения обозначается как р Для 8 - Л/ 16 результат моделирования [82, 83] показан на рис. 11. (а) (б) Рис. 11. Графики гранулированной распределения плотности р (столбец слева) и вероятности2 (столбец справа) для моментов времени t 0, 2л,4л соответственно (а); компьютерная модель релаксации начального неравновесного распределения р = sin2xsin2y (б) 7Г Из графиков на рис. 11 видно, что вероятность 2 имеет свойство возврата к начальному состоянию, что показывает одновременно для свойство равновесия, т.е. имеем 2 . Физически время релаксации для выполнения эволюции 2 для частицы массы m и волновой функции 1 h2 с квантовой энергией уровней перехода E составляет ~ . m ( E)3 Более общее доказательство релаксации 2 можно получить в терминах H - теоремы на основе H-функции H ln / 2dq , которая является аналогом относительной энтропии Кульбака-Лейблера (дивергенция) со знаком минус [42, 43]. Приведем более точные оценки моделирования приближения функции плотности распределения вероятностей. Рассмотрим суперпозицию первых четырех нижних собственных энергетических состояний с эквивалентными весами и различными фазами в следующем виде: 1x1,x2,t eimnmn m,n 1 mnt x,x e sin mx sin nx e m,n 1 m,n 1 i mn Emnt Волновая функция (34) является периодической с периодом 4 . Соответствующий график плотности распределения вероятностей x, x, 0 для t 0 при- веден на рис. 12. (а) (б) Рис. 12. Плотности распределения вероятностей для t 0 и волновых функций и Волновая функция содержит одну составляющую, траектории которой показаны на рис. 13, а, б. (а) (б) Рис. 13. Траектория составляющей и траектории частиц для различных значений ц и f (а) и пространственно-временные траектории составляющей и частицы (б) волновой функции у/ на интервале 0,4Л Рассмотрим также следующую волновую функцию [44]: ^ x,x ,t 3ei 11411 x1,x2 e iE11t + Z 1ei mnфmn x1, x2 e mn , 2 m,n 123 mn2 которая также является периодическая функция с периодом 4 71 , но не содержит других составляю- щих. Соответствующая плотность распределения вероятностей 1^ x,x,0 представлена на рис. 12,б. Для двухмерного векторного поля ai x1,x2, свободного от дивергенции, можно записать ai = 8 ij j f x1, x2, где8 коэффициент антисимметричен и 8 1 (как следствие леммы Пуанка ре), а поле скоростей частицы можно представить в виде: 8а j f x1,x2,t i x1 , x2 , t = 8 s,i x1, x2, t +цij j 122 , (36) к x,x ,t где ц величина постоянная. Коэффициент ц может принимать различные значения, а вид функции f x1, x2 описывается как f = 1^1 , f= 8у i js,j, f3 = д j . Отметим, что значению Ц = 0 соответствует теория Луи де Бройля. Рассмотрим различные неравновесные распределения при t 0 . В Н 2222 этом случае имеем для основного состояния р0x1 , x2 ,0 11x1, x2 I = — sin x1 sin x2 . Другие плотности распределения р , i 1, ,4 получают из р путем преобразований в виде р1 x1, x2,0 4р0 2x1,2x2,0 , р x,x,0 4р 0 2 x1 -л/2 ,2x,0 , р x,x ,0 4р 2x ,2 x -л/2 ,0 , р4 x1 , x2 ,0 4р 0 2 x1 -л/2 ,2 x -л/2 ,0 , x,x е 0, л/2 X 0, Л/2 x,x е л/2,Л X 0, л/2 x,x е 0, л/2 X ^/2,^и x1,x2 2^ Е/2,л^ ^/2,л которые равны нулю вне областей существования аргументов и имеют различные области в четырех квадрантах двухмерного блока. На рис. 14 представлены графики плотностей распределения при различных значениях параметров ци ff при достижении релаксирующей системы равновесия. (а) (б) Рис. 14. Вид аппроксимации плотности 1^ 2 ир (а) и аппроксимации р,рир (б) при t 0,4л,8л и различных значениях параметра ри ff для волновой функции^ 1 Из результатов моделирования, представленных на рис. 14, видно, что релаксация к равновесию осуществляется лучше при больших значениях параметра и. Аналогичный результат моделирования аппроксимации плотностей рир представлен на рис. 15 для различных значений параметра ц. (а) (б) Рис. 15. Вид аппроксимации плотностей р3 и р^ (а) и аппроксимации \ipx |2 и р0 (б) при t = 0,4л, 8л и различных значениях параметра р и f = f для волновой функции \рх y,t = \ip x,y,t |2 [45, 46]. Таким образом, приведено доказательство гипотезы Борна р x, Пример 6: Связь и эквивалентность моделей квантовой механики Шредингера и Гейзенберга. В общем случае для Гамильтониана H€ t квантовой системы, зависящего от времени, эволюция со- стояния определяется как |x, t^ = U€ t, t0 |x) и оператор эволюции U€ t, t0 удовлетворяет Шредин- гер-подобному уравнению ih — U€ t, t0 H^ t U- t, tQ , U t0,t0 =1. (37) dt Оператор должен быть унитарным, который при изменении базиса | x^ I—> |x, t) дает U"1 t,t0 = U t,t0 u£ 1 t0,t . (38) Для волновой функции можно записать р x, t =^x, 11 ip^ = ( xIU t, t0 1^) = ^x| ip. t^ , где как и ранее зависящее от времени состояние вектора определяется в виде| у/, t^ = ?€ t, t0 |у/^ и из (37) удовлетво- ряет уравнению Шредингера Т€|у/,t\ = ih — \t/.Л . Тогда |^,t^ и |x) t являются вектором состояния и собственным значением вектора положения в модели описания квантовой механики Шредингера. В этом случае |^^ и |x, t^ являются эквивалентным описанием модели квантовой механики Гейзен- берга. Данные две «картины» описания в операторной форме квантовой механики эквивалентны и дают одинаковое физическое предсказание наблюдаемых. Волновая функция цг x, t = (x| ^ t) = (x, t|^ по определению является одинаковой в обеих формах описания квантовой механики. Отметим теперь одну из особенностей различия моделей Шредингера и Гейзенберга. Такие операторы как x€ x x x dx , xx в картине Шредингера являются независимыми от времени, тогда как в картине Гейзенберга оператор x t = Jx|x,t^x,t^x является зависящим от времени. В этих случаях имеем x t x^ = xlx^ и xx, t} = x|x,t\ соответственно. Какое соотношение между операторами x€ и x€ t ? Инвертирование соотношения | x, t^ — U€ t, t0 | x^ дает | x = U€ t, t0 | x, t) и тогда (x|xx^ = ^x,t\U€ t,t0 xU t,tQ |x,t^ = ^x,t|.€ t |x,t^, V |x,t^. Для того, чтобы обе картины были эквивалентны необходимо выполнение следующего условия: j€ t =£€ t, tQx€U€ t, t0. Аналогичные условия должны выполняться и для других операторов. Отметим, что коммутатор [.€ t , .€ t ^ ^ 0 и так как: x, i t то должно иметь место соотношение UH H обеих картинах описания квантовой механики. т.е. Гамильтониан сохраняет свой вид в Можно вывести уравнение движения оператора положения частицы в картине Гейзенберга: = -UH€U^U€tjcU^+Uj€tUt€tH€U€ = [x t , т€] Данное уравнение является уравнением Гейзенберга для эволюции во времени оператора положения частицы в картине Гейзенберга. Так как вектор является независимым от времени, то для него не существует уравнения движения в картине Гейзенберга.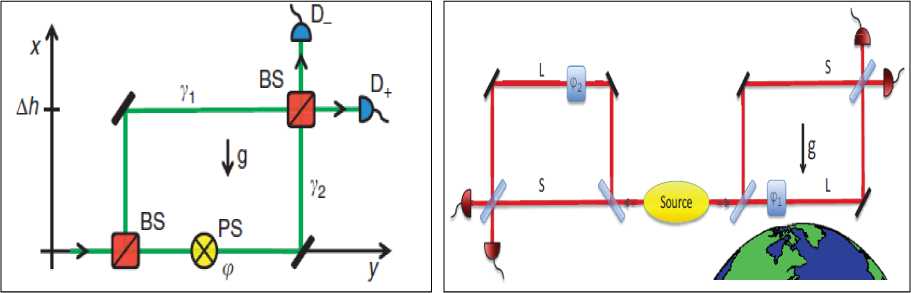
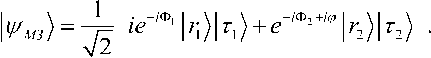
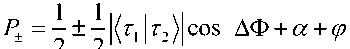
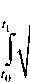
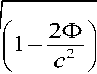
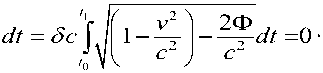
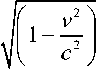
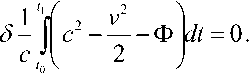
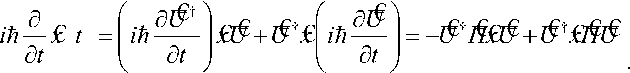
Список литературы Квантовая релятивистская информатика. Ч. 1: модели физических объектов и квантовые релятивистские эффекты в интеллектуальных вычислениях
- Cabello A. Bibliographic guide to the foundations of quantum mechanics and quantum information // arXiv: quant-ph/0012089v12. - 2004.
- Poot M., van der Zant H.S.J. Mechanical systems in the quantum regime // arXiv: 1106.2060 v2 [cond-mat. mes-hall]. - 2011.
- Blencowe M. Quantum electromechanical systems // Physics Reports. - 2004. - Vol. 395. - № 2. - Pp. 159-222.
- EDN: MGKPBP
- Shapiro M., Brumer P. Quantum control of bound and continuum state dynamics // Physics Reports. - 2006. - Vol. 425. - №. 2. - Pp. 195-264.
- EDN: MAGIWB
- Borzı A., Stadler G., Hohenester U. Optimal quantum control in nanostructures: Theory and application to a generic three-level system // Physical Review. - 2002. - Vol. A66. - № 5.


