Квантовая релятивистская информатика. Ч. 2: квантовые вычисления и алгоритмические / физические особенности операторов квантовых алгоритмов

QUANTUM RELATIVISTIC INFORMATICS. PT. 2: QUANTUM COMPUTING AND QUANTUM ALGORITHM OPERATORS

Ulyanov Sergey1, Barchatova Irina2, Reshetnikov Andrey3, Albu Veaceslav4, Averkin Alexey5

¹ Doctor of Science in Physics and Mathematics, professor;

Dubna International University of Nature, Society and Man,

Institute of system analysis and management;

141980, Dubna, Moscow reg., Universitetskaya str., 19;

• ² Senior researcher;

Dubna International University of Nature, Society and Man,

Institute of system analysis and management;

141980, Dubna, Moscow reg., Universitetskaya str., 19;

• ³ PhD student;

Dubna International University of Nature, Society and Man,

Institute of system analysis and management;

141980, Dubna, Moscow reg., Universitetskaya str., 19;

Junior scientist;

Institute of Mathematics and Computer Science;

Republic of Moldova, Chisinau MD 2028, Kishinev, Academiei str.5;

5Candidate of Science in Physics and Mathematics, associate professor;

Dubna International University of Nature, Society and Man,

Institute of system analysis and management;

141980, Dubna, Moscow reg., Universitetskaya str., 19;

Institution of Russian Academy of Sciences Dorodnicyn Computing Centre of RAS;

119333, Moscow, Vavilov st., 40;

Введение: Роль и виды квантовых операторов в проектировании квантовых алгоритмов

Проблему описания и выбора квантовых операторов в квантовых вычислениях рассмотрим с позиции технологии проектирования квантовых алгоритмов (КА).

Большинством гибридных алгоритмов решает задачу, которая в общем виде может быть сформулирована следующим образом:

Вход :  функция f такая, что{0,1} ^и ^{0,1}^т

Задача : найтиопределенноесвойство f .

На рис. 1 изображена общая схема моделирования КА на классическом компьютере.

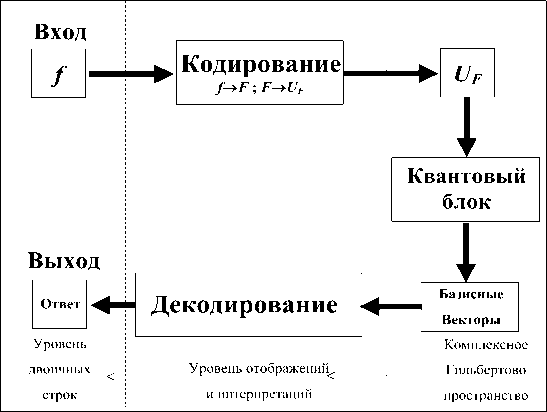
Рис. 1. Схематическая диаграмма квантовых алгоритмов

Очевидно, что для различных КА структура каждого из блоков будет также различаться. Аналогично вид и размерности квантовых операторов также будут зависеть от решаемой задачи, т.е. от типа функции f . Кратко опишем работу данной схемы на рис. 1 и рассмотрим, какие ее элементы имеют отличия для разных типов КА.

Исходная функция f кодируется унитарным матричным оператором U -оператором запутывания (или квантовым оракулом). Процесс кодирования стандартен для всех КА и зависит лишь от вида f . Далее по схеме, оператор U встраивается в квантовый блок, который и выполняет основную работу КА. Он состоит из квантовой ячейки и блока измерений.

Квантовая алгоритмическая ячейка (КАЯ) в свою очередь состоит из оператора запутывания ( U ) и других квантовых операторов (суперпозиции и интерференции). Качество, структура и порядок применения этих операторов будут отличать разные КА. Квантовая ячейка в алгоритме применяется, как правило, к одному и тому же начальному базисному вектору. В результате ее применения получается состояние суперпозиции, содержащей часть ответа на исходную задачу. Блок измерения извлекает информацию о полученном решении.

Таким образом, результатом однократного применения квантового блока служит часть ответа (в виде одного базисного вектора) на поставленную задачу. Чтобы получить полный ответ, необходимо повторить квантовый блок k раз – число, зависящее от задачи и алгоритма.

Работа квантового блока может быть представлена квантовой схемой рис. 2.

Далее, коллекция базисных векторов интерпретируется блоком декодирования, который также является проблемно зависимым. Результат, полученный в классическом виде (как правило, в двоичном виде) может использоваться в дальнейших вычислениях или быть прямым ответом на искомую задачу.

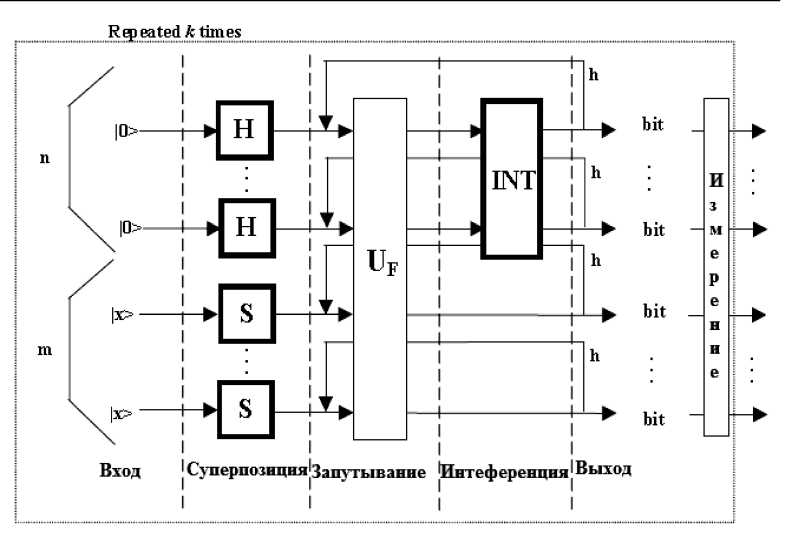
Рис. 2. Квантовая схема работы квантового блока (H – оператор Адамара (суперпозиции),

S – некоторый оператор, INT – оператор интерференции)

В матричной форме процесс проектирования КАЯ заключается в проектировании трех квантовых операторов: суперпозиции (Sup), квантовой корреляции (запутанных состояний – entanglement U ), и интерференции (Int), и составляют основу структур КА. В общем виде структура КАЯ может быть представлена в виде КАЯ Int n I U      nH m S , где I – оператор идентичности; – символ тензорного произведения; S равен I или матрице Адамара и выбор зависит от описания исследуемых свойств функции. Таким образом основу КА составляют операторы квантовой суперпозиции, оператор запутанных состояний (квантовой супер-корреляции – entanglement или квантовый оракул), интерференции и измерений.

Элементы теории квантовых вычислений

С точки зрения применения теории квантовых вычислений в прикладной системной инженерии квантового программирования выделяют два направления исследований:

• -    задано множество точек функционала S = x, у , необходимо найти вид такого оператора

U , чтобы выполнялось условие y U x ;

• -    задана проблема (квантовый алгоритм – КА), необходимо найти вид квантовой алгоритмической ячейки (схемы) – КАЯ, решающей заданную проблему (реализующей данный КА).

В качестве примера рассмотрим традиционный математический формализм описания моделей основных квантовых операторов, т.е. с точки зрения второй квантовой проблемы описания КА. Данный формализм может быть выражен на языке квантовых состояний или преобразований, но имеется также возможность адекватного описания квантовых состояний и эффектов на языке логического вывода: применение традиционного формализма, его мощности и выразительности как квантовой системы нечёткого логического вывода. В данном разделе рассмотрены вопросы описания и интерпретации квантовых операторов, применяемых в квантовых вычислениях, квантовых

Электронный журнал «Системный анализ в науке и образовании» Выпуск №4, 2013 год алгоритмах и квантовой теории информации² для практического применения в теории интеллектуальных систем управления.

Ввиду ограниченного объема, необходимые сведения из теории квантовых вычислений и квантовой теории информации излагаются на конкретных примерах, используемые при изложении на конкретных примерах применения в реальных объектах управления. Дополнительную информацию о методах квантовых вычислений читатель может найти в рекомендуемой литературе [1-27].

Основные понятия и определения теории квантовых вычислений: квантовый бит (кубит) и особенности квантовых вычислений

Введем на примерах необходимые понятия и определения из теории квантовых вычислений.

Пример 1: Квантовый бит как квантовое физическое состояние . Классический бит может находиться в одном из двух состояний: 0 или 1. Таким образом, его физическое состояние можно представить как b a 0 a 1 , которое имеет одну из форм: или a 1 и a 0 , тогда b 0 , или a 0 и a 1 , и тогда b 1 . В противоположность состояние квантового бита 1^) задается вектором в двухмерном комплексном векторном пространстве. Здесь вектор имеет две компоненты, и его проекции на базисы векторного пространства являются комплексными числами. Квантовый бит у/ представляется (в обозначениях Дирака в виде кет -вектора) как И=«| 01 или в

4'") =

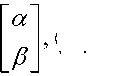
W = а Р ^T ( бра -вектор). Если  1^)⁼ | 0) , то I 0) =

векторном обозначении

.

Амплитуды ОС и р – комплексные числа, для которых выполнено следующее условие: аа + РР* = 1, где «*» – операция комплексного сопряжения; пара I0) и 1 образует пару ортонормальных базисных векторов, называемых состоянием вычислительного базиса . Если ОС или р принимают нулевые значения, то у определяет классическое, чистое состояние. В противном случае говорят, что у/ находится в состоянии суперпозиции двух классических базисных состояний.

Геометрически квантовый бит находится в непрерывном состоянии между I 0) и 1 , пока не производятся измерения его состояния. С учетом условия нормировки можно опустить фактор глобальной фазы и записать вектор 1^/ в более удобном виде как 1^) = cos — I0^ + ei ф sin 1 , где 6иф изменяются в области от 0 до 2 л . В данном случае вектор 1^) описывает точки на поверхности сферы Блоха, как это представлено на рис. 3.

Оси x , y , и z представляют геометрически собственные состояния вектора трех наблюдаемых, известных как матрицы Паули:

0

1

1^

0,

0

i

i

0

^{и G}z

10

01

.

Каждая матрица Паули имеет два собственных значения, +1 и – 1.

Значения собственных состояний данных трех наблюдаемых приведены в Табл. 1.

Таблица 1. Собственные вектора и собственные значения матриц Паули

наблюдаемая	собственное значение	собственное состояние
x	±1	1 x , ±1      1■10 1
y	±1	1 y ,   1       1     0 i 1
СУ	±1	1 z , 1   0 , z ,11

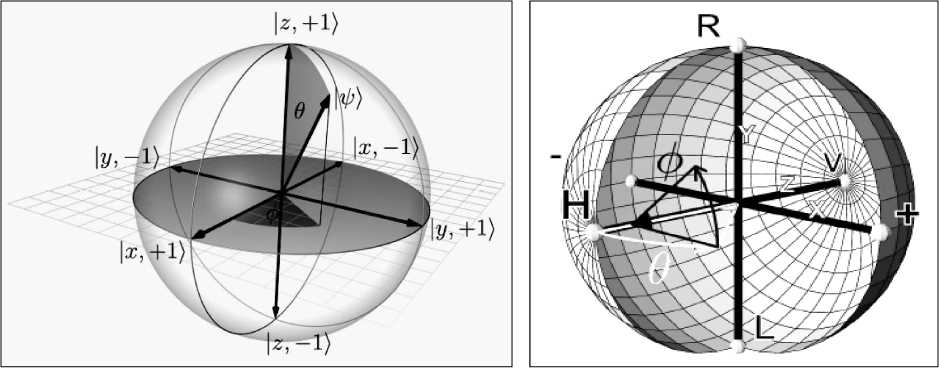
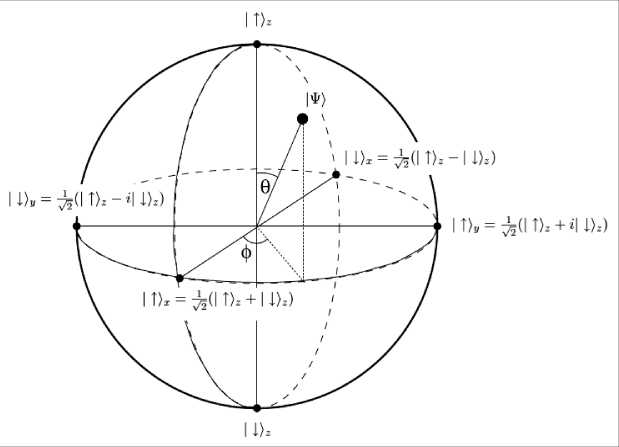
Рис. 3. Представления сферы Блоха

Ортогональный к 1^) вектор имеет вид

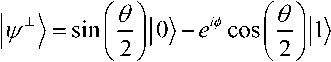
и соответствующая

наблюдаемая для состояний

к) и к1)

имеет следующее представление:

67 6 ,Ф = sin О cos ф ст + sin о sin ф ст + cos 6 су .

Физический смысл матриц Паули следующий: матрица о изменяет вычислительный базис кубита ос |01 на ОС |10 ) ; аналогично операция СУ осуществляет смещение состояния на фазу 71 и умножение состояния 1 на минус 1. Данные операции справедливы только в вычислительном базисе, например, в базисе СУ данные действия обратимы.

Пример 2: Геометрические преобразования квантового бита. Показанное в Примере 1 стандартное представление сферы Блоха для состояния простого кубита можно описать в терминах матрицы плотности состояния с применением унитарной 22 матрицы и применением некоторых особенностей матриц Паули. Чистое состояние кубита 1^) можно рассматривать в виде точки комплексного пространства □ P1 , представляет собой единичный вектор в □ 2 с точностью до глобальной фазы. Без потери общности можно записать

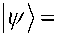
cos

eiф sin к 2)

где 0 <0 <л и

02 ТС (фактор ½ для О выбран так, чтобы данные области соответствовали областям изменения

сферических координат). Значениям о =0 и 0 = л соответствуют состояния I0 ) и 1 . Таким образом, пространство состояний простого кубита соответствуют топологии сферы с единичным радиусом.

Рассмотрим однозначное соответствие между чистыми состояниями кубита и точками единичной сферы S ² в о ³ . Такое соответствие называется представлением сферы состояния кубита (см. рис. 3). Вектор Блоха для состояния кубита 1^ определяется как:

r x , y , z

, где 5

x sin О cos ср , y sin о sin ср , z cos .

Матрица плотности для состояния

1^) определяется как:

х?=ии = 1

1+ cos 0 e^iф sin 0

e i sin1

I+xаx+yаy+zа,

1 cos       2x      yz

где x , y , z определяют координаты вектора Блоха и матрицы:

I

0А

1) J 0 i

0 ; ^, y     _{i 0}

(10А

z

называются матрицами Паули. Тогда матрицу плотности р можно записать в компактном виде как

и r векторы Блоха двух чистых

состояний

, то имеем

¹+ r ₁ r ₂

, т.е. имеем однозначное

соответствие внутреннего произведения в О2 ио 3 . Отметим, что для ортогональных квантовых состояний имеем К^71 1^2)| =0 и тогда rr 1 и rr, т.е. соответствуют полярные точки на сфере Блоха.

ортогональные состояния

Рассмотрим другую геометрическую интерпретацию вектора 1^) для простого кубита в виде

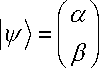
•       6

1 ,

еО 2 , которое полностью определяется второй компонентой р =ei sin . Так как то множество чистых состояний кубита может быть идентифицировано на единичном диске в комплексной области (с полярными координатами для (3 в виде r,ф , где r = sin — ).

Определим соотношение С —— как «линию комплексного переменного» для состояния ^ , так как все точки этой линии эквивалентны точкам линии . Для чистого состояния кубита имеем

= e^l(p cot— . Данное представление не избыточно, так как состояниям |0) и |1) соответствуют значения ^ = оо и 4 =0. Таким образом, имеем однозначное соответствие между чистыми состояниями кубита и расширенной комплексной плоскостью 0 _ю = 0 U ⁰⁰ .

Допустим, что U

ab cd

унитарная матрица и преобразует состояние |^ в виде

U

a

b

ab cd

ab ab

. Введем новое соотношение С, =------- =------ (деление на

cd cd

нуль возможно в силу свойств расширенной комплексной плоскости). Тогда оператору U соответствует следующее преобразование переменной 4" g .z : f £ = где выполняются

d граничные условия f

a

—. Поскольку преобразование и унитарно, то

cc det U aad-bc ^ 0, и преобразование f переменная функция.

Такое преобразование является специальным аналогом конформного преобразования, называемого линейным дробным преобразованием или преобразованием Мёбиуса.

-

Понятие стереографической проекции сферы Блоха на x, у - поверхность (см. рис. 4).

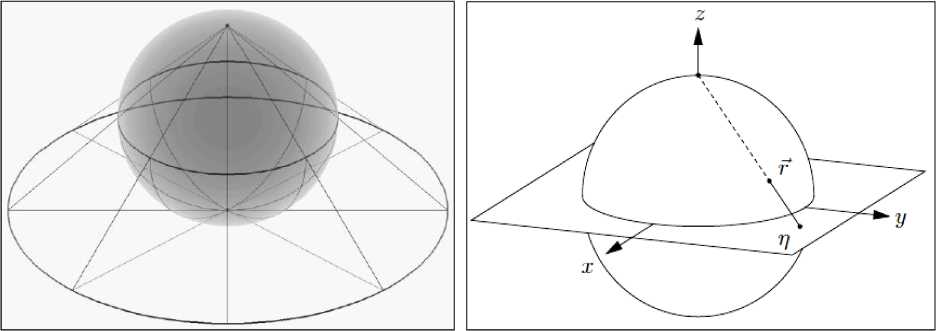
(а)                                                       (б)

Рис. 4. Стереографическая проекция как гомеоморфизм отображения в S ² (а) и стереографическая проекция сферы Блоха на расширенную комплексную плоскость (б)

Рассмотрим рис. 4б. Для определения проекции вектора Блоха r — x , у, z проведем линию соединения северного полюса z и вектора r , т.е. определим точку пересечения г] проекции r с x, у -поверхностью (рис. 4б). Для определения проекции р будем интерпретировать r как параметрическое семейство x + zy , z еП х□ =□ ³. Тогда р является положительным множителем для x + zy .

<        „   „   ^1 x + iy

.

Из рис. 5, а видно, что              и поэтому ту —----- x+ iy 1 z                 1 z

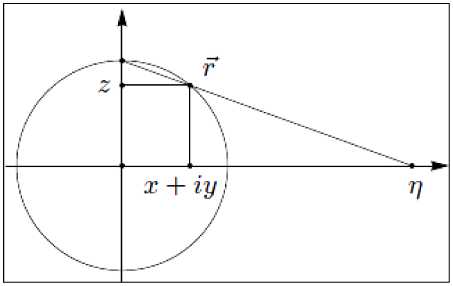
(а)

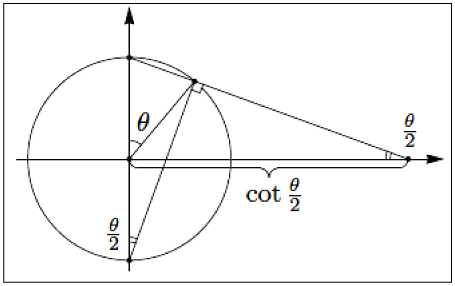
(б)

Рис. 5. Проекция ^пв r x⁺iy , z (а) и геометрическая интерпретация члена cot ₂ (б)

Отметим, что северный полюс r 0, 0,1 проектируется в Т] = со . Тогда для чистого состояния

• О кубита ^ =ei cot имеем соотношение £ = Л = x ,y ,z являются координатами вектора Блоха.

x iy

1 z,

т.е.    комплексно сопряжено с ту и

Геометрический смысл определения ^ = eⁱ cot представлен на рис. 5б. Непосредственно из

д рис. 5б следует, что фактор cot соответствует расстоянию проекции до оригинала или упрощенно до абсолютного значения величины .

Формализм описания сферы Блоха можно представить также в виде расслоения Хопфа трехмерной сферы S ³ в пространстве □ ⁴ . Идентифицируем □⁴ иО ² в виде

x

y

z

x+ iy z+ iw

.

w

Тогда сферу S3 можно определить как S321 . Допустим, что д еП и является

единичным вектором //£S ³ . Тогда «комплексная линия» в направлении // определяется как Lc д| c еП . Допустим, что C определяет пересечение L и S ³ : C L Ц S ³ e^iф /z|^eD . Отметим, что C определяет окружность S ¹ на поверхности S ³ и для каждой точки //е S ³ окружность C однозначно определена и содержит параметр ц .

Таким образом, поверхность S ³ можно рассматривать как семейство окружностей S ¹ .

• -    Визуализация полного пространства Гильберта S ³ с расслоенной структурой в R ³ . Рассмотрим возможные варианты визуализации полного S ³ пространства Гильберта с расслоенной структурой. Это можно осуществить^3,4 (прямым) стереографическим отображением S ³ в R ³ (рис. 6, а ).

  

  (а)                                       (б)

  Рис. 6. Расслоение Хопфа сферы S ³ после стереографического отображения в R ³ (а) и семейство вложенных торов с параметризацией 6 6 0, и (б)

  
  

Расслоения могут группироваться в конечное семейство вложенных торов, три из которых показаны на рис. 6а. В общем случае проективное отображение из северного или южного полюсов 0,0,± 1   в плоскость экватора определяется как:

P : Sn\ 0,   0,  1        n, p

pn1       P1

PN,0

p1

1pn1,

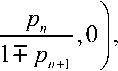
и обратное отображение

P1:  □nSn\ 0,0, +1 ,    P1,   ,PN,0       p1,   ,pn+1

2 P 1

P2 +1,

2Pn    P2  1

P2 +1,  P2 +1J

где P ²   P ² + ...+ P ² . Теперь можно представить в визуальном виде расслоение сферы S ³

стереографической проекцией на пространство о 3 плоскости экватора. Введем параметризацию 6          о а = cos  ei 1, Р = sin ei 2 в соответствии с выражением для матрицы плотности кубита при ф — ф    . Для вложенного тора и глобальной фазы л имеем       22

cos2

2

.

Стереографическая проекция в обратном представлении задается как:

2 x 2 y 2 z r ²   1

,,,

( r ² 1 r ² 1 r ² 1 r ² 1)

P1: □ 3 S3 \ 0,0,0,±1 ,   x, y, z ,0 м а,а, /) ,Р

2222      ² 22

где r   x ²   y ²   z ² . Поскольку |а| = а ²² , то, применяя полученное обратное преобразование,

2       2

получим:  y cos

x2 + y2 + 1 . Данное уравнение описывает поверхность в о 3, которое инвариантно при вращениях вокруг 3-осей, так как только сумма xy присутствует в уравнении. Если принять y 0 в 1-3- плоскости, то имеем:

/            X 2

2xо

-^—зcos , x2z2+12

О cos

² е

1   tan ²

2 о          2

cos ²

.

Отсюда следует, что данное соотношение определяет окружность с радиусом

о tan и центром в

точке

,0,0

cos

. Вращение вокруг 3 – осей воспроизводит торус. Поэтому поверхность y ² задает

семейство вложенных коаксиальных торов с параметризацией 6 6 0, л (рис. 6б).

• -    Визуализация полного пространства Гильберта S ³ с расслоенной структурой в □ ⁴_. С целью визуализации данной ситуации, введем сферические координаты в □ ⁴ и применим стереографическую проекцию для проектирования S ³ на более широкое семейство пространства □ ⁴ . По аналогии описания S ³ в о ³ координаты единичного вектора //еП ⁴ можно задать как

x sin а sin Р sin У y sin а sin Р cos У                         ~

, где а , Р ^G 0, Л и/ G 0,2 71 .

z sin а cos Р w cos а

В этом случае окружность C в 4 – мерном мире для ц =

x+ iy z+ iw

по аналогии с ранее

введенными определениями для 3 – мерного мира можно представить в следующем виде:

Cei ,

^ =

	cos ф	sin ф	0	0	гx
(x+ iy ж	sin ф	cos ф	0	0	y
z+ iw	0	0	cos ф	sin ф	z
	0	0	sin ф	cos ф )	w J

.

проекции

По аналогии с ранее введенной стереографической

из S ² в □ можно ввести

x

обобщение в виде:

y

z

1 w

x

y

. Выбирая единичный вектор //еП 4 и подставляя

z

w соответствующие значения

а , Р и У можно вычислить окружность C и ее проекцию в ³

согласно приведенным выражениям.

В результате получаем пространство □ 3 , заполненное полностью окружностями в том смысле, что каждые две окружности попарно связаны друг с другом.

Результат вычисления приведен на рис. 7 (вертикальная линия соответствует состоянию

71             71

«окружность на бесконечности»). Тору соответствует a = — и P ⁼k , где k 0,1, 2, 3, 4 .

При k 0 и k 4 тор вырождается и соответствует линии и окружности соответственно. При фиксированных параметрах a и P данные окружности соответствуют при различных У охватывают поверхность тора.

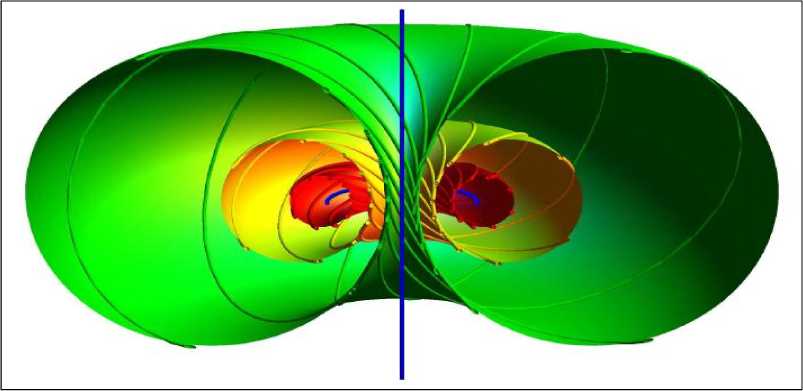
Рис. 7. Стереографическая проекция расслоения S ³

Примеры таких торов приведены на рис. 8.

Рис. 8. Три примера торов образуемых при k 1 на рис. 7

Физическое различие между классическим и квантовым битами показано для наглядности на рис. 9.

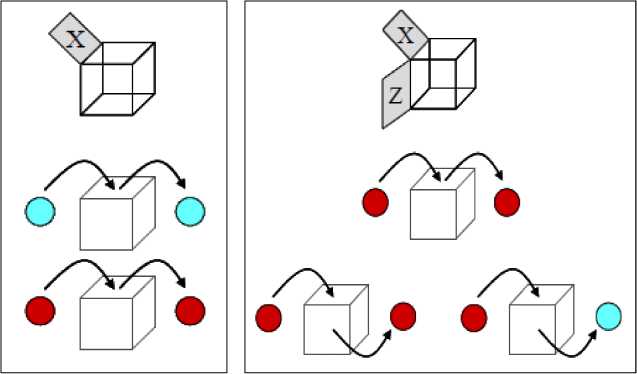
(а)                                (б)

Рис. 9. Классический бит (а) и квантовый бит (б)

На рис. 10 показан физический механизм изменения качественных свойств квантовой системы в зависимости от условий взаимодействия с внешним прибором.

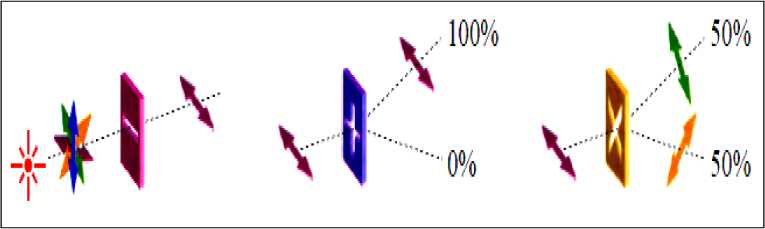
• (а)                      (б)                          (в)

Рис. 10. Физическая реализация кубита как поляризованного фотона

Так в случае, представленном на рис. 10,а, фотоны из источника с горизонтальной поляризацией проходят через линейный поляризатор и формируется кубит с заданной поляризацией, в этом случае с горизонтальной поляризацией фотонов. В случае, представленном на рис. 10,а, фотоны с горизонтальной поляризацией из источника проходят через линейный поляризатор с вертикальной и горизонтальной поляризацией, но как и в первом случае имеем фотоны с горизонтальной поляризацией. В третьем случае (рис. 10, в ) поляризация в разделителе фотонов имеет диагональные поляризации. Поэтому фотон с вероятностью 50% может быть в обеих формах поляризации (но измерение дает только одну из форм поляризации). При повторном измерении фотон будет обнаружен с данной формой диагональной поляризации, т.е. измерение изменяет состояние фотона. Понятие амплитуда вероятностей квантового состояния является комбинацией концепции состояния и фазы.

В случае, когда система состоит из двух квантовых битов, она описывается как тензорное произведение. Например, в обозначениях Дирака двухуровневая бит система задается, как

1    2    12 V^aA 00) + a^|01 VPy\ 10)+^l11).

Число возможных состояний комбинированной системы возрастает экспоненциально при добавлении квантового бита. Это приводит к проблеме оценки квантовой корреляции, которая присутствует между квантовыми битами в составной системе.

Рассмотрим пример, который иллюстрирует принципиальные отличия квантовых вычислений от классических (в общем случае вероятностных) вычислений.

• - Отличие квантовых вычислений от классических вычислений . В классических вычислениях, основанных на булевой логике, один бит информации представляется в виде состояний 0 или 1. Два

бита представляют четыре состояния 00, 01, 10, и 11; n бит могут представить 2 ⁿ состояний. В квантовых вычислениях квантовый бит (кубит) является системой из двух составных состояний в виде одного бита информации. Физически один электрон может моделировать кубит. Направления состояния спина «вверх» и состояния спина «вниз» электрона представляют два состояния 0 и 1, соответственно. Фотон также может представлять физическое состояние кубита, а его горизонтальная и вертикальная составляющие поляризации могут реализовать оба состояния одновременно.

Важное и принципиальное отличие заключается в том, что один кубит представляет собой суперпозицию состояний 0 и 1. Поэтому можно представить состояния 0 и 1 кэт - векторами 0 и 1 , соответственно, так, что состояние суперпозиции представляет линейную комбинацию 0 и 1 в виде       a 0 b 1 , где коэффициенты a и b представляют значения амплитуд вероятностей.

Поэтому, согласно постулату Борна (см. ниже Пример 5), величина a 2 является вероятностью, что вектор суперпозиции        0 после измерения кубита       a0b1 и b2является вероятностью, что вектор суперпозиции       1 после измерения кубита      a0b1. Тогда a2b21 в соответствии с законом сохранения вероятности полного события. Если, в частности, амплитуды  вероятностей a и b равны  1 /  2 , то имеем состояние суперпозиции a 1/  2  0 b 1/  2 b 1 , а вектора 0    1,0 T и 1    0,1 T .

При измерении состояния суперпозиции      состояние 0 наблюдается (измеряется) с вероятностью 1 /  2    1 / 2 и 1 также с вероятностью 1 /  2    1 / 2 . Такое необычное для булевой логики свойство квантовых вычислений создает возможность параллельных массивных вычислений. Поскольку каждый кубит представляется двумя состояниями, то два кубита представляются четырьмя состояниями одновременно. Например, если использовать в качестве входных сигналов два кубита в суперпозиционном состоянии 0 и 1, то в результате обрабатываются четыре операции для четырех входных сигналов для четырех выходных сигналов за один шаг, в то время как на классическом компьютере требуется для обработки четыре шага. Для n кубитов суперпозиция из 2n состояний составляет входной сигнал и решение проблемы осуществляется за один шаг, в то время как для классического компьютера требуется 2n шагов.

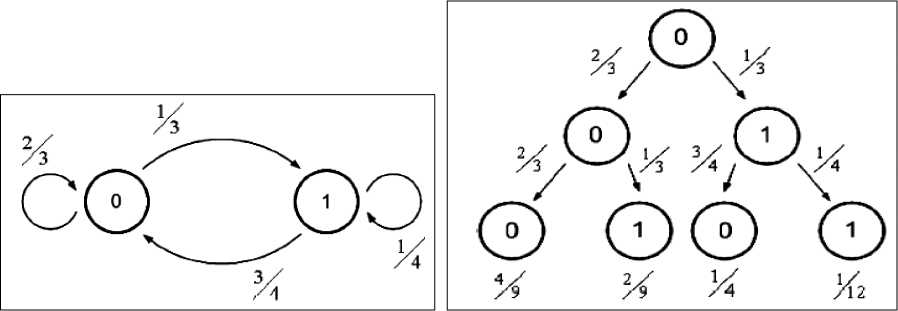
Сравним теперь отличие и результаты работы классического и квантового компьютера на примере вероятностной классической и квантовой машин Тьюринга для выяснения роли интерференции в квантовых вычислениях. В качестве модели машины Тьюринга (рис. 11, а) рассмотрим дерево вычислений, представленное на рис. 11, б, в.

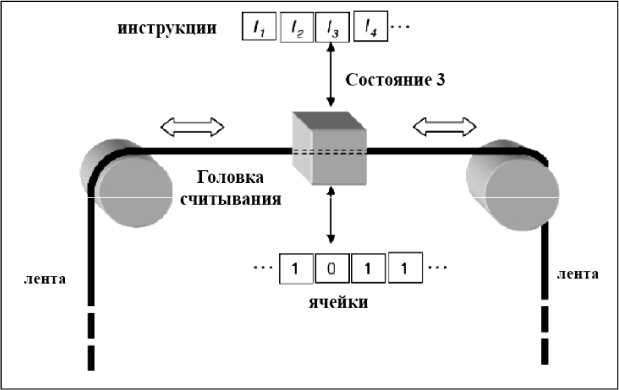
(а)

(б)                                                      (в)

Рис. 11. Машина Тьюринга (а) диаграмма перехода состояний (б) и дерево вычислений вероятностной машины Тьюринга (в)

На рис. 11 вершина дерева означает состояние машины Тьюринга, ребро означает вероятность события перехода. Уровень дерева означает шаг вычисления, а источник вершины дерева представляет состояние старта вычисления.

Вычислительный процесс, т.е. временная эволюция машины Тьюринга, определяется т.н. переходной функцией : зависимости от текущего состояния управления qQ и символа      , обозначающий ячейку ленты, в которой находится головка считывания машины, машина Тьюринга переходит в некоторое новое внутреннее состояние qQ, записывается некоторый символ в данную ячейку ленты и затем перемещается влево L или вправо R . Таким образом, функция перехода 8 является отображением: 5 : Q х ^ —Q Qx^x L,R .

Например, рассмотрим машину Тьюринга с алфавитом Z = 0,1,# , внутренним состоянием

Q = q ₀, q_x , q^  и функцией перехода 8 в виде:

q0,0 —^qx ,1, R q о,1       ^ qi,0, R qi,0^Uqi,1,R . qv1 —^Я1,0, r qP# —^qf ,#, R

Состояния 8 q ₀,# и 8 q^,a для некоторого а определяются как функция аргументов. Допустим, что данная машина Тьюринга стартует с некоторым входным битом s полосы, который записан в сегмент ленты |^0# 5 — 1J . Головка машины установлена в нулевой ячейке. Вычисление на машине Тьюринга осуществляет изменение полосы и процесс останавливается.

Например, на рис. 12 отображены первые шаги временной эволюции машины Тьюринга для входа 5 = 10 .

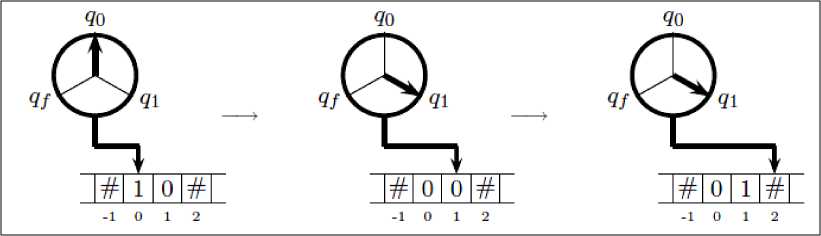
Рис. 12. Временная эволюция машины Тьюринга

Квантовая машина Тьюринга определяется по аналогии с машиной Тьюринга, но с очень важным отличием, что функция перехода описывается амплитудой перехода. Вместо простого классического состояния для каждого внутреннего состояния и символа ленты, в квантовой машине Тьюринга задается суперпозиция различных классических состояний.

Например, допустим, что квантовая машина Тьюринга с управляемым внутренним состоянием qQ и символом ленты 0 переходит во внутреннее состояние q и записывается 1 и головка сдвигается вправо, а если записывается 0, то сдвигается влево, но при этом оба состояния 1 i одновременно находятся в суперпозиции с комплексными амплитудами    и    .

Данная операция в символьном виде представлена на рис. 13.

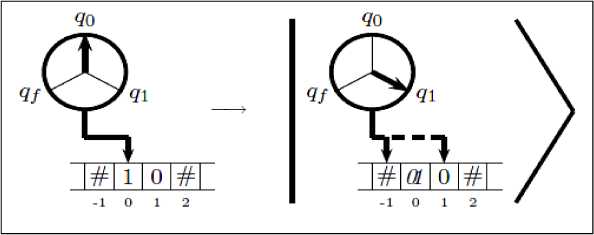
Рис. 13. Один шаг временной эволюции квантовой машины Тьюринга

Для данного варианта вычисления можно записать амплитуду перехода как отображение q ₀,0 -^ q ,1, R q ,0, L .

1 i

Формально амплитуда перехода 5 является отображением Q х 52 в комплексные функции на Q X 52 X L , R . Если квантовая машина Тьюринга функционирует в Гильбертовом пространстве состояний, то амплитуда перехода линейно расширяется до определения глобальной временной эволюции на данном Гильбертовом пространстве и является унитарной. Вычислим вероятность перехода 0 1 после двух шагов вычислений, просуммировав вероятности двух возможных путей из вершины в состояние 1 следующим образом:

P 01

— X —

— X —

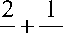
Аналогично P 00

— х —

— х —

4  3   25

-+— = — .

9  12  36

Таким образом, за два шага

вычислений стартуя из состояния 0 вероятностная машина Тьюринга перейдет в состояние 1 с вероятностью 11/36 и в состояние 0 с вероятностью 25/36.

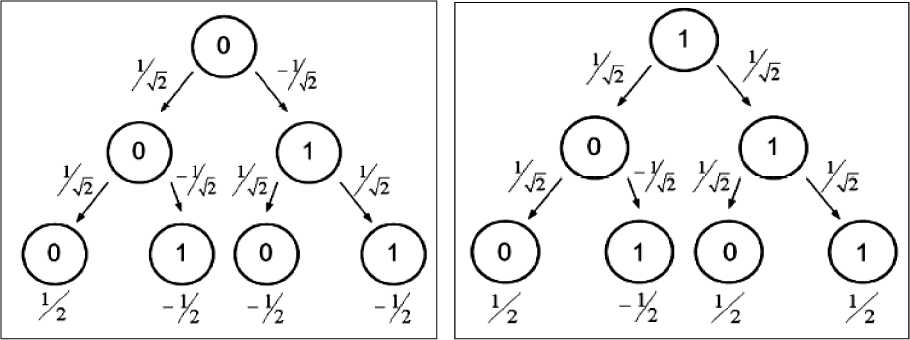
- Интерференция квантовых вычислений . По аналогии с вероятностной машиной Тьюринга, опишем вычисления на квантовой машине Тьюринга, используя дерево вычислений, представленное на рис. 14.

(а)                                                (б)

Рис. 14. Вычисления на кантовой машине Тьюринга (а) – старт из состояния 0; (б) – старт из состояния 1

Отметим одну из особенностей квантовых вычислений на квантовой машине Тьюринга, которая связана с явлением квантовой интерференции амплитуд вероятностей. В квантовой машине Тьюринга каждое ребро представляет амплитуду вероятностей, в то время как в вероятностной машине Тьюринга каждое ребро представляет вероятность перехода. Только одно состояние обрабатывается на заданном уровне в заданный момент времени в вероятностной машине Тьюринга. В квантовой машине Тьюринга, напротив, все состояния на заданном уровне в квантовой машине Тьюринга обрабатываются одновременно. Например, вероятность события перехода 0 1 из источника вершины после одного шага вычисления определяется как

г1 ² 1

V V2)   2

и вероятность

события перехода 00 при таких же условиях определяется как

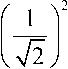
. Вычислим теперь

вероятность перехода 0   1 после двух шагов вычислений. Во-первых, необходимо найти амплитуды вероятности по двум возможным путям перехода: ^0   0   1 и^ 0   1   1 , т.е.

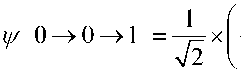
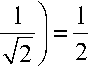
у 011

Сложим обе амплитуды вероятностей событий перехода

.

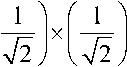
у/ 0  1 после двух шагов) = у/(0  0  1>^011

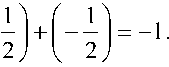
Таким образом, вероятность перехода 0   1 после двух шагов определяется как

P 0   1 после двух шагов J= 1^ (0   1 после двух шагов

Аналогично вычисляется вероятность перехода 00 после двух шагов в виде:

^ 0  0  0   1   1  1, у/010

2   22

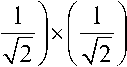
2 ^,

V 0  0 после двух шагов) = у/ (0  0  0>^001   ¹

0 ,

P 0   0 после двух шагов

= 1^(0   0 после двух шагов )    0    0 .

Получили замечательный результат. После одного шага вычислений вероятности перехода 0   1 и 00 были обе равны ½. Но после двух шагов вычислений из одного источника вершины вероятность перехода 0   1 равна 1, а вероятность перехода 00 равна 0. Данный результат возможен в силу свойства амплитуды вероятностей принимать отрицательные значения и означает, что состояния квантовой машины Тьюринга интерферируют друг с другом.

В этом случае, переход « 0   1 после двух шагов» имеет конструктивную интерференцию

1^ - 1/2  + - 1/2 J = - 1 , а « 0   0 после двух шагов» имеет деструктивную интерференцию

[ 1/2 + - 1/2 ] = 0 .

• - Оператор плотности . В квантовой механике квантовое состояние     выражается операто

ром плотности состояния p . Матрица плотности p квантовой системы имеет следующие свойства:

• ^†= p (эрмитова матрица); p > 0 (положительная матрица); Tr p ⁼ 1 (нормированная матрица). Если состояние квантовой системы известно точно, то система описывается оператором плотности в матричном виде p=MW и находится в чистом состоянии. В противном случае система пребывает в смешанном состоянии. В этом случае имеем смесь из различных чистых состояний, описываемую оператором плотности p = pw      в ансамбле p ,   ) . Матрицы, удовлетворяющие

i перечисленным условиям, образуют выпуклое множество. Поэтому они могут быть записаны в виде p = pw к ^Pк , где 1^k - единичные векторы Гильбертова пространства и p0, p1 . kk

Коэффициент p для заданного k может интерпретироваться как вероятность нахождения квантовой системы в чистом состоянии 1^k . Однако данная физическая интерпретация зависит от представления p~^LpW к ^Pк | , которое не является однозначным: разные состояния могут иметь k одинаковую матрицу плотности.

В частности, векторы могут быть выбраны ортонормальными и интерпретированы как собственные векторы  матрицы  плотности P   с собственными  значениями p , а формаP~^Lpw     называется спектральным  представлением p . Чистые  состояния

k представляют собой одномерные проекторы I^X^I и являются экстремальными точками выпуклого множества матриц плотности.

Таким образом, на основе матриц плотности чистых состояний воспроизводятся все остальные матрицы плотности, соответствующие смешанным состояниям как выпуклая комбинация в виде p = ^ pw     , но сами они не допускают описания в виде нетривиальной выпуклой

k комбинации других матриц.

Существует простой критерий определения типа состояния квантовой системы: если след матрицы плотности Tr ²   1 , то квантовая система находится в чистом состоянии; если

Tr 2   1 , имеет место смешанное состояние. Определение и вычисление следа оператора плотности дано ниже.

С точки зрения теории информации, в квантовом бите содержится точно такое же количество информации, как и в классическом бите, несмотря на бесконечное множество виртуальных состояний квантового бита. Квантовый бит может быть описан бесконечным числом суперпозиций классических состояний, но из-за необратимого характера процесса измерения можно извлечь только простой классический бит информации из одного среди возможных состояний. При этом остальные виртуальные состояния разрушаются, и происходит потеря информации. Основанием для данного утверждения (в квантовом бите содержится не больше количества информации, чем в классическом бите) является тот факт, что информация извлекается в результате физического процесса измерений.

За счёт измерения квантового бита происходит изменение его состояния и в результате он переходит в одно из возможных базисных состояний. Каждый квантовый бит существует в двухмерном пространстве, его измерение ассоциируется с соответствующим базисом и выражает результат только в одном из двух состояний, т.е. один из базисных векторов ассоциирован с данным измерительным прибором.

Таким образом, как и в классическом случае, при измерении квантового бита существует только два возможных результата. Поскольку измерение изменяет состояние квантового бита, то невозможно осуществить одновременно регистрацию состояния в двух различных базисах. При моделировании классической динамической системы, её состояние можно измерить на первом этапе в одном базисе, затем - на втором этапе в другом базисе.

В истинно квантовой системе подобное действие невозможно, так как при измерении происходит разрушение волновой функции описывающей состояние квантового бита. Более того, квантовые состояния в истинно квантовой системе невозможно клонировать, т.е. существуют объективные физические ограничения, в силу которых не удаётся проводить измерение двумя разными путями, используя, например, копирование квантового бита и его регистрацию в различных базисах.

В отличие от квантового бита состояние классического бита можно копировать и осуществлять измерение в различных вычислительных базисах. Более того, неизвестный квантовый бит нельзя «расщепить» на взаимно дополняющие части, т.е. содержащаяся в неизвестном состоянии квантового бита информация неразделима.

Примечание 1. Вычислительный базис +/ ,    . Для описания и измерения квантового бита ранее использовался вычислительный базис I0 , 1  . Однако такой выбор вычислительного базиса не является единственным. Возможно использование различных множеств векторов в качестве ортонормальных базисов. Например, базисные векторы допустимо представлять в виде состояний

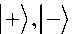
определяемых как

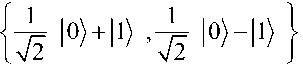
соответственно. Используя данное представление базисных векторов, можно перейти к традиционному базису:

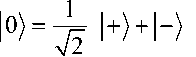
и 1   ¹ ₂ КМ-)

Следовательно, в квантовой механике допустимы операции, невозможные в классической механике. И, наоборот, в классической механике существуют операторы решения задач, недопустимые в квантовой механике.

Алгоритмические особенности формирования квантовых операторов суперпозиции, запутанных состояний (entanglement), интерференции и измерений

Операторы суперпозиции, квантовой корреляции (запутанные состояния - entanglement) и интерференция являются основными операторами проектирования квантовых алгоритмов. Рассмотрим кратко алгоритмические особенности, физические основы и результаты экспериментальной проверки данных операторов.

Пример 3: Формирование состояния суперпозиции с помощью оператора Адамара (Уолша-Адамара). Существование состояния суперпозиции и эффекта измерения квантового состояния физически означает, что присутствует скрытая от наблюдателя информация , которая содержится в замкнутой квантовой системе (до момента ее возбуждения от внешнего возмущения) в виде наблюдения квантового состояния. Система остается замкнутой до взаимодействия с внешней средой (т.е. до действия наблюдения системы).

Важнейшим в этом случае является следующий вопрос: как эффективно использовать скрытую в суперпозиции информацию?

В традиционном формализме квантовых вычислений квантовые операторы описываются в эквивалентной матричной форме. Умножение матрицы оператора на вектор состояния означает действие операции на исследуемую систему. Например, действие матрицы Адамара H на систему

1^) ⁼ I 0 может быть представлено как

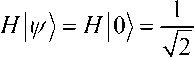
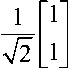
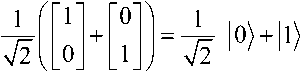
Аналогично, HH 1 ^,                21   1

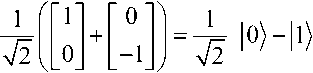
т.е. преобразование Адамара порождает состояние квантового бита в виде суперпозиции двух классических состояний.

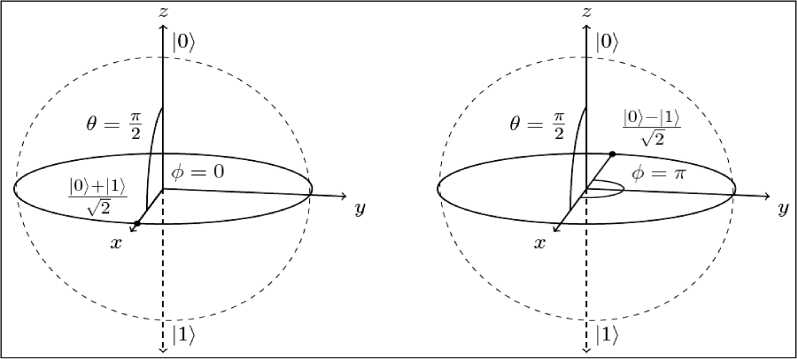
На рис. 15 показано действие оператора Адамара.

Формирование суперпозиции с эквивалентными амплитудами вероятностей - важный шаг для многих КА. Применяя H ⁿ на соответствующих базисных состояниях x H, x е 0,1 ⁿ , получим в результате эквивалентную форму преобразования Адамара:

H x     ¹         1 xz z , где x z  x ₁ z ₁ + ...+ x z для x 0 и x 1 .

2 z 0,1

(а)                                (б)

Рис. 15. Представление оператора Адамара на сфере Блоха для базисного состояния 0 ) (а) и для базисного состояния 1   (б)

Пример 4: Квантовый параллелизм и модели вычислений с квантовым оракулом . Рассматриваемый эффект является одним важнейших в квантовых вычислениях и используется (так же как и суперпозиция) во многих моделях КА. Он особенно широко применяется в различных моделях «чёрного ящика» или «квантового оракула» при проектировании разного класса КА, например, для вычислений функций следующего вида: g : 0,1 n —> 0,1 m . Поскольку отображение x —> x , g x , xe 0,1 n обратимо, то существует унитарное преобразование U_g , эффективно моделируемое классическими вычислениями x , g x так, что | x , у)—>|x , y®g У )для некоторого ye 0,1 m . При этом дополнительные квантовые биты, необходимые для реализации обратимых схемных преобразований, здесь не рассматриваются. Преобразование U , описывающее «чёрный ящик» (как частный случай U ), представляет унитарное преобразование в виде Булевой функции f : 0,1 n —> 0,1 . Если | у ) - начальное состояние |0) , то после применения преобразования U_f выход преобразования f x будет | x , f x ^. Физический смысл квантового параллелизма заключается в наличии эффекта параллелизма вычислений после использования преобразования U для суперпозиционного состояния, представляющего различные значения x . Так применяя U к состоянию

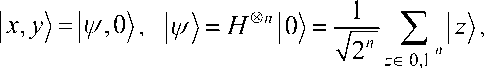
имеем в результате иД iff ,0^=  ,— ^ | z , f z ^, т.е. суперпозицию всех возможных значений

2 n ..^n n вычисляемой функции. Таким образом, применение только одного шага для оценки значений функции fx является достаточным для вычисления параллельно значений fx от всех возможных входных аргументов x .

Данный эффект эквивалентен применению свойств «чёрного ящика» (одноразовое применение внутренней квантовой схемы). Однако в действительности только одно значение функции fx доступно при измерении результата вычисления fx в суперпозиции возможных состояний, так как из-за эффекта разрушения состояний в суперпозиции доступно только одно случайно измеренное состояние. Обсуждение выбора модели квантового оракула для КНВ и его обоснование дано ниже.

Примечание 2. О вычислении значений функции с помощью фазы . Применение оператора U к

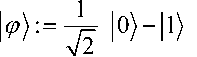
даёт следующий

управляемому квантовому биту в состоянии суперпозиции результат:

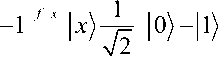
= -1 ^fx |x,(p)

U_f\x,(/Д = -^ |x , f x )-|x ,1® f x

Опуская | ф^ , можно определить новое преобразование типа V^ : | x ) —>^_ 1 f x | x ).

Следовательно, V позволяет вычислить значения функции fx через фазу. Другими словами, вычисление возможно через преобразование значений f из базовых состояний в амплитуды относительно данных базовых состояний.

Теперь, применяя V к вектору , получим следующее состояние:

и = V f       ¹ _n        1 ^fxz .

2 z 0,1 ⁿ

Это соответствует применению к управляемому квантовому биту операции

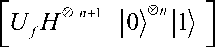
Пример 5: Моделирование квантовой корреляции (запутанных состояний – entanglement) с помощью CNOT-подобных операторов . Корректная оценка вычислительной мощности квантовых вычислений возможна только с помощью установления корреляций между значениями переменных в КА в различные моменты времени. В качестве примера рассмотрим систему из двух квантовых битов A и B . В соответствии с законом тензорного произведения векторных пространств размерность пространства H составной системы AB определяется как произведение размерностей пространств H _A и H _B , т.е. как H H ® H . Вычислительный базис состояний I 00 ) ,I 01}, I 10 ,11 для составной системы AB выражается через базисные состояния систем A и B I 0 , 1 тензорным произведением: I xx )⁼ I x I x ,V x , x е 0,1 ² .

При этом в составной системе квантовых битов существуют состояния, которые не могут быть выражены через тензорное произведение отдельных компонент квантовых бит. Это свойство называется запутыванием (entanglement) или неразделимостью (nonseparability) квантовых состояний. Допустим, что WAB  состоит из двух состояний. Если существуют два состояния \ф ) в HA и 1^в в H , такие, что |^AB     A     B , то состояние называется разделимым (или unentangled). В противном случае оно является запутанным (entanglement) или неразделимым (unseparable). В качестве примеров можно привести систему из двух квантовых битов известную как состояния Белла или ЭПР - состояния (в честь пионеров этих примеров Белла и Эйнштейна, Подольского и Розена):

¹00   11  ;          ¹01н10) ^.

Когда производится измерение таких состояний, как подсистем в составной системе запутанных состояний, то при известном результате об одном состоянии подсистемы можно точно определить состояние другой подсистемы (без проведения над ней измерений). Поэтому существует другой вариант в интерпретации таких состояний: если рассматривают одно из состояний как запутанное, это означает, что состояние нельзя факторизовать в состояние произведения из подсистем двух состояний.

Таким образом, если применяется оператор к одной из компонент запутанного состояния, то результат действия не факторизуется по остальным компонентам, а вычисляется для этих компонент непосредственно по одной из измеряемых компонент. Действуя оператором Адамара H на состояние

П

Белла на первую компоненту, в результате получим

H1 1   00   11     1   H1 I 0) I0)+ H1 1 1    1 I 00)+|10н 01н11), или в матричной форме

H ¹ = I 00 ) + |11      ¹

12                   2

т.е. имеем новое запутанное состояние, которое используется в обратной связи квантового генетического поискового алгоритма для обогащения квантовой корреляции запутанного состояния.

Последовательно действуя на вторую компоненту полученного состояния оператором Адамара H , приходим HH 1  00) + |11

V2

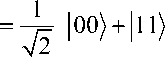
К сожалению, сложность реализации операций квантовыми ячейками в данном подходе возрастает с числом запутанных состояний связанных с управляемым битом.

Примечание 3. Эффективное моделирование КА на классических компьютерах . Запутанные состояния в квантовых вычислениях рассматриваются как дополнительный физический ресурс, позволяющий существенно увеличить расчетную мощность по сравнению с классическими моделями вычислений. Число параметров, необходимых для описания незапутанных (чистых) состояний в заданном Гильбертовом пространстве H (представленных как тензорное произведение квантовых битов), возрастает только линейно с увеличением числа n квантовых битов. Однако для описания общего вида состояния (незапутанного или запутанного) требуется экспоненциальное число 2 ⁿ векторных коэффициентов. Поэтому вопрос о физическом ресурсе квантовых вычислений не имеет простого ответа.

Данная проблема обсуждалась в деталях с общих позиций теории квантовых вычислений. Было показано, в частности, что для КА (оперирующих чистыми состояниями) для повышения эффективности по сравнению с классическими аналогами с увеличением размерности входных квантовых битов требуется неограниченное число запутанных состояний. Более того, эффективно КА можно моделировать классическим инструментарием (классическими алгоритмами) только при наличии малого количества квантовой корреляции и фиксированном уровне толерантности вычислительных операций в КА. Было показано, как можно эффективно классическими алгоритмами моделировать КА со сравнительно слабой квантовой корреляцией.

Вычислительная стоимость возрастает линейно с числом входных квантовых бит и экспоненциально - с увеличением требуемого количества квантовой корреляции. Независимое обобщение такого подхода приведено в данном разделе и разработано соответствующее программноаппаратное обеспечение для эффективного моделирования КА на классических компьютерах. Этот подход использован для моделирования в реальном времени робастных БЗ для интеллектуальных нечетких регуляторов.

Изложенные аргументы и результаты свидетельствуют о предпочтительной роли квантовой корреляции как движущей силы квантовых вычислений (на чистых состояниях эволюции квантовой динамики).

Пример 6: Моделирование квантовой интерференции с помощью преобразования Адамара и квантового преобразования Фурье (КПФ). С целью повышения вероятности измерения и извлечения искомого (маркированного) решения основной единой идеей в процессах проектирования моделей КА служит использование явления конструктивной / деструктивной интерференции в качестве инструментария извлечения результатов эффективных вычислений КА. Для увеличения вероятности извлечения «успешного» решения применяется конструктивная интерференция, а для редукции

«плохих» решений - деструктивная интерференция. Конструктивный (деструктивный) эффект можно проиллюстрировать наглядно на примере применения преобразования Адамара к состояниям

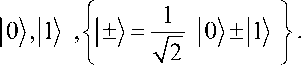
Очевидно, что H0      и H1      , т.е. воспроизводится состояние суперпозиции классических состояний в виде квантовых битов. При этом применение преобразований Адамара к состояниям I0) и 1 порождает состояния с одинаковым распределением вероятностей. Поскольку состояние |+/ является суперпозицией обоих классических состояний I 0/и

1 , то при повторном применении преобразовании Адамара к |+) классическая модель логического вывода (модель Колмогорова) предполагает одинаковую вероятность результирующего классического состояния (принцип сохранения вероятности). Однако вследствие оперирования в квантовых вычислениях с понятием амплитуды вероятностей применение преобразования Адамара к состоянию |+) дает следующий результат: H      1             0).

Таким образом, проявился эффект интерференции между вероятностями обоих классических состояний. Интерференция (в силу своего физического характера) усилила амплитуду вероятности одного ( I0 ) ) классического состояния (конструктивная интерференция) и ослабила существенно (до нуля) амплитуду вероятности другого ( I 1у ) классического состояния (деструктивная интерференция). Действуя на суперпозицию возможных решений, интерференция реализует процесс формирования финальной фазы квантовых вычислений и является (так же, как и квантовая корреляция) физическим ресурсом усиления квантовых вычислений, а также для решения различных проблем проектирования моделей КА. Например, применяя преобразование H n к состоянию 1^') в виде (П2.1), получим в результате квантовое состояние вида

1 _n ■ z z -¹

xz+fx z ,

2 nn z 0,1    x 0,1

служащее основой для проектирования квантовой ячейки, например, при решении проблемы Deutsch-Jozsa.

В модели КА Шора при факторизации произведения на простые числа интерференцию обеспечивает оператор КПФ: оператор QFT I действует на каждый базисный вектор, принадлежащий линейной комбинации исходного вектора 1^) . Это означает, что любой вектор в такой комбинации воспроизводит суперпозицию базисных векторов. Комплексные весовые коэффициенты базисных векторов равны по модулю (т.е. амплитуды вероятностей равны), но имеют различные фазы. Каждый базисный вектор является взвешенной суммой амплитуд вероятностей, полученных из разных последовательностей базисных векторов.

Данная сумма может увеличивать или уменьшать результирующую амплитуду вероятностей. Так как этот эффект подобен эффекту интерференции классических волн, то говорят что оператор играет роль оператора интерференции. С

QFTn         exp < 2 71 J ij     2n

i 1 j 1

2 ⁿ

математической точки зрения, когда оператор QFT I действует на состояние, то все столбцы результирующей матрицы задействованы при вычислении и интерференция осуществляется между весовыми коэффициентами из разных последовательностей базисных векторов. Рассмотрим теперь особенности очень важного (и часто дискутируемого в работах по описанию основ квантовой механики) квантового оператора, описывающего необратимый процесс извлечения результата квантовых вычислений.

Пример 7: Измерения в разных вычислительных базисах . Постулат квантовых измерений был введен фон Нейманом. Рассматривались только проективные измерения, в которых «стандартные» квантовые наблюдаемые A имеют спектральное представление в терминах ортогональных проективных операторов. Постулат утверждает, что во время измерения A вектор состояния квантовой системы редуцируется в собственный вектор наблюдаемой A , соответствующий результату измерения. Таким образом, базис основного подхода к построению моделей процессов измерений в квантовых вычислениях составляет постулат о проекциях фон Неймана: результат действия наблюдения состояния V над наблюдаемой A как результат измерения есть одно из собственных значений A ,т.е. измерение разрушает состояние V и ренормализует его.

Для конечномерного Гильбертова пространства математически это означает следующее: пусть H – Гильбертово пространство размерности n квантовой системы S. Допустим, что n                       n

AP – спектральное представление наблюдаемой A , где X – собственные i 1 i 1

значения и ф. - собственный вектор, соответствующий X. ; ф₁ ^ ^

- ортонормальный базис

пространства H и P - проекция на собственное пространство оператора A (натянутое на собственные векторы) с собственными значениями Д •

Возможное значение проективного измерения отвечает собственному значению Д наблюдаемой

n

A . Наблюдаемая A состояния |^) = ^|^) воспроизводится как значение А. с вероятностью i 1

k cij j1

, где c,,cтакие, что                              , и при этом состояние системы i1              ik                                     i1            i2                        ik1            iki

k после измерения определяется как j1

i j

•

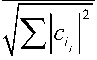
Таким образом, до измерения для квантовой системы в состоянии |у/^ возможный результат измерения определяется как p m      P_m    , а после измерения система ренормализуется в

состояние

.^m     . Полнота уравнений устанавливается фактом из теории вероятностей:

1 = ^ p m =^l!/\P mV Y mm

Постулат о проективных измерениях получил развитие в разных направлениях.

-

Постулат обобщённого квантового измерения . Модель обобщенного квантового измерения

(замкнутая квантовая система S в конечномерном пространстве состояний) описывается набором М_т операторов измерений на Гильбертовом пространстве H квантовой системы S , где индекс m указывает на возможный исход (результат) процесса измерений. Операторы измерений удовлетворяют условию полноты: ^ М ^f М_т = I • m

Если состояние системы S есть | Ц/^ до измерения, то вероятность получить выходное значение m определяется как p m = М\М \ M m \у/ ) . В последнем выражении и далее символ «f » означает операцию сопряжения унитарного оператора. После измерения система S ренормализуется как M

. Из данной модели измерений как частный случай следуют модели проективных измерений и положительно-определённые операторно-значимые (ПООЗ) меры измерений. Так, например, если M удовлетворяет двум дополнительным ограничениям: M M† , M M M , то получим представленную ранее модель проективных измерений. При выполнении условия E = МfМт, имеем ПООЗ меры измерений.

В квантовой теории информации существуют строгие правила и законы, описывающие процессы извлечения информации из неизвестного квантового состояния. Результат проективных измерений квантовых битов должен быть сформулирован в классических терминах. Более точно любое проективное измерение одного квантового бита приносит только один классический бит информации. Поэтому, несмотря на существование бесконечного множества возможных квантовых состояний квантового бита, эти состояния не различимы. Не существует процессов измерений в рамках модели фон Неймана, с помощью которых можно извлечь информации больше чем один ожидаемый бит информации из квантового бита. Идентификация состояния квантового бита не является полной, т.е. для неизвестного состояния квантового бита |^ с помощью проективных измерений невозможно определить его истинное состояние. Измерение состояния квантового бита 1^ =a0b1}, соответствующее наблюдению O,O (гдеO (O ) – подпространство, натянутое на состояние I0 (I1 ), или, другими словами, в соответствии со стандартным вычислительным базисом I 0 ,1 ), имеет выходным результатом бит 0 (1) с вероятностью a 2 ( Ib I 2 ) и состояние 1^ =a0b1} коллапсирует в состояние I0 ) (I1 ). Вся другая информация, содержащаяся в суперпозиции, необратимо потеряна. Поэтому для наблюдателя квантовый бит представляется как случайная величина с определенным распределением вероятностей.

Однако квантовый бит 1^ ⁼ a 0 b 1 можно измерить также относительно других вычислительных базисов бесчисленным образом.

Например, часто используется дуальный вычислительный базис

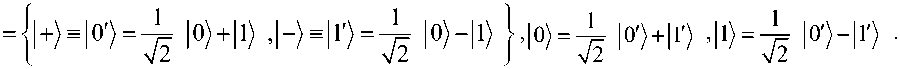
и измерение I ^) в этом базисе дает 0 (или 1) с

Тогда

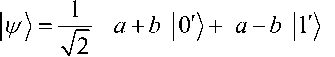
вероятностью ab ²

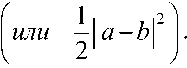
Примечание 4. Квантование классических операторов в различных вычислительных базисах (о соответствии квантовых и классических операторов). Рассмотрим в качестве примера проблему «квантования» заданного классического оператора. Допустим, что классическим оператором является однобитовая операция отрицания «НЕТ» (NOT gate), которая конвертирует бит a в его дополнение

1 a, a0,1 . Нетрудно показать, что в качестве квантовой составляющей этой операции достаточно выбрать унитарную матрицу Паули типа Сх =

. Однако

если принять операцию

отрицания квантового бита в виде матрицы у aa , где

(1 a

a

, то выполняется точно

отношение у ^x      . С другой стороны, матрица Паули o_z

также реализует

операцию отрицания «НЕТ»: л<

при условии, что вычислительный базис выбран другим

образом, т.е. в виде Л aa , где a

1 ^a

.

Данный простой пример показывает зависимость процедуры установления квантовоклассического соответствия от выбора состояний в вычислительном базисе. Более того, даже если

выбран вычислительный базис, существует множество вариантов для дальнейшего

описания

операции. Так, например, если выбрана операция у , то оператор дX ⁼

0   eⁱ ^

eⁱ^     0

тоже

реализует

конвертирование бита У x      для заданных значений углов 6,ф . Стандартная операция

отрицания при е = ф = 0 является только вариантом, но не единственно возможным. Этот факт объясняется физической природой квантовых состояний, которые описываются лучами, а не векторами в Гильбертовом пространстве. Приведенные аргументы имеют место и при установлении обратного соответствия между квантовыми и классическими операторами, т.е. квантовому оператору могут соответствовать разные классические операторы.

Так, например, оператору    соответствуют как операция идентичности:       z     , так и отрицания:       z

Рассмотрим пример применения моделей измерений в квантовых вычислениях. Пусть задана составная квантовая система из двух квантовых битов в виде вектора состояний в комплексном пространстве C ⁴ в вычислительном базисе:

|^) = а ₀| 00> + a 1| 01) + a ₂| 10) + а ₃| 11) . (3)

Отметим, что (3) является обобщённым запутанным состоянием. Если измеряется первый бит в состоянии , то существуют две возможные ситуации результата измерений ( m 0,1): первый бит равен нулю ( m = 0), или он равен единице ( m = 1).

В первом случае соответствующий оператор обобщённого измерения определяется как M 0   00 00   01 01 . Во втором M1   10 10   11 11 . Вероятность события «первый бит в состоянии | Ц/^ есть нуль» вычисляется в виде p 0 = ^ |МJМо | у/^ = |а012 + |а1|2. После измерения M0         M0          a0 00 a1 01

состояние определяется как W     .     = .             = —..

p 0         M0†M0          a02

Во втором случае вероятность, что первый бит в состоянии | Ц/^ есть единица, вычисляется как p 1 = М\М^М_х |у/^ = | a ₂1² + | a ₃1² и после измерения состояние системы описывается в следующем

M1          M1          a2 01

.

p 1         M1†M1          a22

Для рассматриваемого примера оператор обобщённого измерения Мт можно определить через операторы проективного измерения:   Мо = Po + Pv Мх = Po + Pxx, где  Po,Pt,Po,Pxx  -

соответствующие проекции на пространство 000    00 C4 0 следующего вида: 0    00 0 0 0 0 0 0 0 P 00     0 0 0 00 00, P0 0 0 1 0 0 0 0 P 0,   0 0 0 0 0 0 1 0 0 ,P 0 0 0 0 0 0 0 0  , 0 0 00 0 0 0 0 0 0 0 0 0 0 0 Г где P00  P0   P 0 P = I 4 и I4 идентичный оператор в C4. Матрицы M0, M являются двухмерными проекторами в C2 ® C2 и могут быть переписаны в виде блочных матриц: I2 0 00 M0 0 0 , M 0 I2 где I2 - идентичный оператор в комплексном пространстве C2. Нетрудно проверить прямым вычислением, что выполняется следующее необходимое условие:

М J М_о+М f М_х = 1⁴ .

Рассмотрим соответствующую взаимосвязь с ПООЗ-мерами измерений. В этом случае для двух ПООЗ-мер, следуя определению, верны следующие соотношения:

E « = М 0 М 0 = М 0 , E , = М ' М, = М, и E 0 + E = I ⁴ .

Аналогично приведенному выше варианту измерений, если измеряется второй бит в состоянии , то существуют два других варианта возможных результатов измерений ( m 2,3): или второй бит нуль, или единица. В первом варианте соответствующий оператор обобщённого измерения - 27

М 2 ⁼ |00^00| + |10^10| и для второго случая М 3 = |10^10| + |11^11|, где M P P , M P P . Очевидно, что данные измерения с возможными значениями ( m = 2,3) отличаются от предыдущего варианта ( m = 0,1).

Рассмотрим особенности обсуждаемого формализма описания квантовых процессов измерений на важном примере обобщенных измерений состояний Белла.

Напомним, что четыре состояния

являются максимально запутанными и образуют базис запутанных состояний в пространстве C ⁴ . Их часто называют «магическими» в силу необычных физических свойств и важной роли в квантовых вычислениях.

Выделим частный случай: 00 11 . Если измерять первый бит в , то, как и ранее, существует два возможных варианта результата измерений ( m 0,1): или первый бит нуль, или единица. Для случая m = 0 имеем ранее приведенный вариант обобщённого измерения М _о.

Вероятность, что первый измеренный бит в состоянии |^⁺^ будет 0, определяется в виде I = ^⁺ | М J М_о | ф⁺ ^ ⁼ 2 . После измерения имеем квантовое состояние:

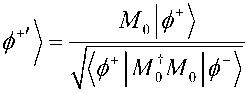
¹ ₂ 00

Для случая m = 1 справедлива аналогия варианта обобщённого измерения М ₁. Вероятность, что первый измеренный бит в состоянии |^⁺^ равен 1, вычисляется как p 1 = ^^⁺| М^МДф⁺^ = ^.

После измерения получим квантовое состояние

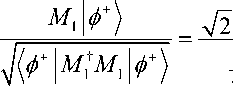
, и как

результат p 0 + p 1 =—+—=1 (закон сохранения вероятностей). Отметим, что операторы М^,

М_х являются ПООЗ-мерами для обобщенных наблюдаемых.

Отметим один из физических «парадоксов», связанных с процессом измерения - квантовый эффект Зенона. Квантовый эффект Зенона состоит в замораживании (или замедлении) эволюции системы, подвергающейся частым и точным измерениям.

Пример 8: Эффект Зенона. Фундаментальное правило, открытое Борном и фон Нейманом, и определяющее статистический аспект квантовой теории, гласит, что вероятность обнаружить систему в состоянии при условии, что она была приготовлена в состоянии , задаётся квадратом модуля их скалярного произведения: F . Введённая величина F называется степенью согласованности или вероятностью совпадения квантовых состояний (fidelity). Если, например,

а |^) = |0), то ^|^ = -^= и F — —. Допустим, что в начальный момент времени волновая функция свободной частицы в импульсном представлении имеет вид:

1        2 ^pp ²²                                                                     p € ²

pe0 . Используя гамильтониан свободной частицы H     получим оператор p0                                                   2m p€2t эволюции U€  e2m и в момент времени t волновую функцию:

_p 2       _{p 0} 2 _t

1 i

1        2 p2    2m p,t    U€t  0 p              e 0        .

p ₀

Амплитуда обнаружения частицы в момент времени t в начальном состоянии    задается скалярным произведением        t1 i

p 0 ² t

1/2

2 m

. Соответствующая вероятность:

P 0 t

p 0 ⁴ t ²

2 m ^{2 2}

1/2

₁ p 0 ⁴ t ²

8 m ^{2 2}

Если на протяжении времени T сделать N измерений с интервалом t T / N , то суммарная вероятность ухода частицы из состояния составит:

P ухода T , N N 1   P 0 T / N

_T 2    _{p 0} 4

N 8 m ^{22 .}

Тогда при N имеем P _ухода T , N 0 , т.е. частые измерения, определяющие осталась ли частица в прежнем состоянии, «останавливают» движение частицы. С помощью эффекта Зенона можно не только «замораживать» эволюцию системы, но и вести эту эволюцию произвольным образом, т.е. можно задать состояние системы как функцию от времени и реализовать эволюцию системы по заданному пути с точностью до фазовых множителей. Такой эффект принято называть эффектом Антизенона .

Рассмотрим кратко физические особенности квантовых операторов, применяемых при конструировании квантовых алгоритмов.

Физические особенности формирования квантовых операторов суперпозиции, запутанных состояний и интерференции

Квантовые операторы суперпозиции, запутанных состояний и интерференции формируют неклассические состояния, свойства которых существенно отличаются от классических состояний.

Рассмотрим функцию, которая может быть использована для описания неклассичности квантового состояния, функцию Вигнера – функцию квазивероятностного распределения, определенную в фазовом пространстве5.

• -    Функция Фигнера и ее свойства . Имея волновую функцию   ( Q )    Q |     чистого квантового состояния    , функция Вигнера может быть определена как:

W Q , P = — jm Q + y U(Q-y ) e^2iPy^dy.                   (4)

Приведем основные свойства функции Вигнера:

QQ Q , P dQdP = 1 , Q Q, P dP |Щ 0 )|²,   WWQ, P dQ = Щ P )|²      (5)

и

¹ W ( Q , P )    ¹ .                                         (6)

TIKI                 ЛК1

Последнее свойство (6) показывает, что функция Вигнера может принимать отрицательные значения. Физическая интерпретация данного свойства означает, что такая отрицательная часть функции Вигнера может быть индикатором присутствия квантовой природы^6,7.

Кратко поясним смысловое содержание данной физической интерпретации: чем меньше отрицательное значение функции Вигнера, тем более классическим является поведение системы.

В этом контексте вводится параметр (  ) в виде:

5 Щ := J j| Q ( X,P )| dXdP -1 .                         (7)

Часть данного параметра равна модулю интеграла волновой функции квантового состояния фазового пространства, в котором функция принимает отрицательные значения.

Говорят, что состояние является полуклассическим, если удовлетворено условие (  )   1 .

При этом рассматриваются также «участки» отрицательности функции Вигнера исследуемых состояний. Структура отрицательных секторов может раскрыть некоторые глубокие аспекты квантовых механизмов при их описании в фазовом пространстве.

Рассмотрим наглядные примеры. В первую очередь обсудим физический смысл выражений (5) – (7) на примере состояний «кота Шредингера» для гармонического осциллятор на конфигурационном пространстве q , p с массой m и частотой .

• -    Кот Шредингера . «Мысленный» эксперимент, проведенный Шредингером, о существовании неразличимого состояния одновременно «живой – мертвый» кот до измерения получил название «Шредингеровский кот». Состояние кота Шредингера определяется как суперпозиция двух таких состояний. Если выбрать два когерентных состояний локализованных в двух различных точках конфигурационного пространства q , то волновая функция такого состояния для квантового осциллятора в представлении положения q можно записать как:

N         mm2p q             q       q , где q           exp         q  q0i 0 q  q0. (8)

Рассмотрим, как влияет параметр p на форму функции Вигнера, в частности при q 1 оба волновых пакета не разделены в пространстве. Функция Вигнера для когерентного состояния имеет вид:

exp ipx dx , W q , p dqdp 1 .     (9)

Подставляя (8) в выражение для функции Вигнера (9) получим:

W  q , p W q , p W  q , p   W _int q , p .                    (10)

• ⁶    A. Kenfack, K. Zyczkowski, Negativity of the Wigner function as an indicator of non-classicality // J. Opt. B: Quantum Semiclass. Opt. – 2004. – Vol. 6. – pp. 396 – 404 (доступно arXiv: quant-ph/0406015v1 2 Jun 2004).

• ⁷    C. Gehrke, Quantitative characterization of nonclassicality. – Diploma Thesis. – Univ. of Rostock. – 2008.

Тогда удвоенный интеграл по объему интегральной отрицательной составляющей функции Вигнера можно записать в виде (7) как:

= JU W q, p W q, p dqdp W q, p I dqdp 1.

По определению величина 8 у< равна нулю для когерентного и сжатого вакуумного состояний, для которых функция Вигнера неотрицательна. Параметр 5 цг характеризует свойства рассматриваемого состояния относительно отрицательной составляющей функции Вигнера и описывает эффекты интерференции, которые определяют отличие рассматриваемого состояния от

классического

поведения.

N ²               2

W q , p      exp ^q±q ₀ p  p ₀

2 7Г

Для

рассматриваемого

функция имеет

два

случая

имеем

пика распределения,

сконцентрированных в точке классического фазового пространства

N ²                   2

W _int q , p       cos 2 pq exp   q ²

7Г

±q ₀, p ₀

, и

p  p 0

и описывает структуру интерференции, которая возникает между обоими пиками.

1/2

Из условия нормирования (8) следует N 1 + cos 2 p q exp q ²    . Применяя формулу (10)

для функции Вигнера состояния кота Шредингера 1^) , получим выражение для параметра неклассического состояния в виде §    = |л W q, p + W q, p + Wint q, p dqdp 1 , которое можно аппроксимировать в виде 8 4х

N ² 1 + j dp ^1cos 2 p ₀ q ₀ I exp p p ²

В специальном случае q 0 суперпозиция когерентных состояний (27) в простое когерентное состояние и соответственно параметр неклассичности б Т = 0.

На рис. 16 представлены графики поведения функции Вигнера для состояния кота Шредингера для заданных значений параметров разделенных позиций q и момента p .

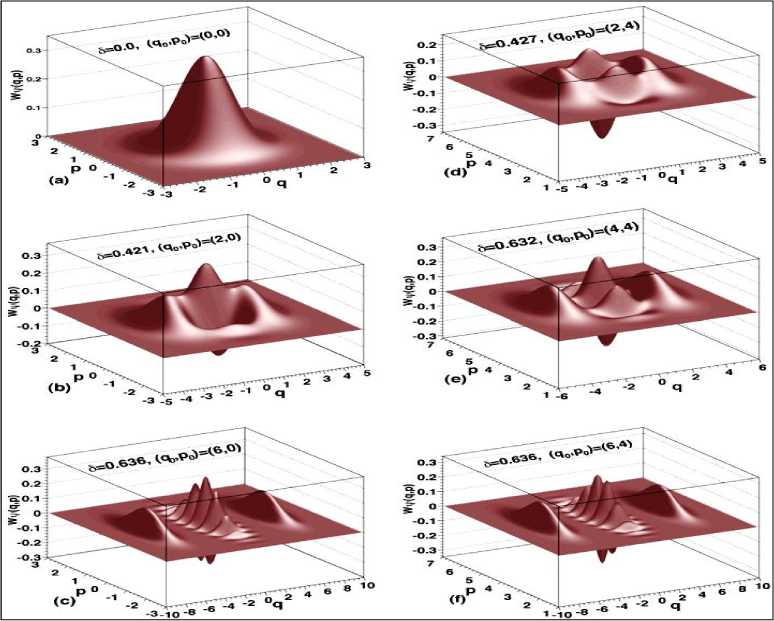
Рис. 16. Графики поведения функции Вигнера для кота Шредингера при различных значениях параметров q0, p0

Из результатов, представленных на рис. 16 следует, что формирование структуры квантовой интерференции увеличивается вдвое между локальными пиками при возрастании разделяющей дистанции q . При этом частота структуры интерференции возрастает при увеличении параметра q . Отметим некоторые качественные особенности поведения функции Вигнера в разных областях изменения параметров  q0, p0. В промежуточной области изменения параметра разделения состояний 0q0 4 функция Вигнера существенно меняет свою структуру при изменении момента p (см. рис. 16b,d). Однако для больших значений разделяющей состояния дистанций, q 4 , функцию Вигнера для pp^ 0 можно аппроксимировать функцией Вигнера для состояния с параметром p 0 с переносом постоянным вектором 2^pp1 .

Приведенная картина поведения функции Вигнера становится боле сложной для состояний с параметром p ^0 , в частности для малых разделяющих расстояний 0 q 4 .

В этом случае параметр 6 начинает осциллировать как показано на рис. 17 и при этом отличен от нуля.

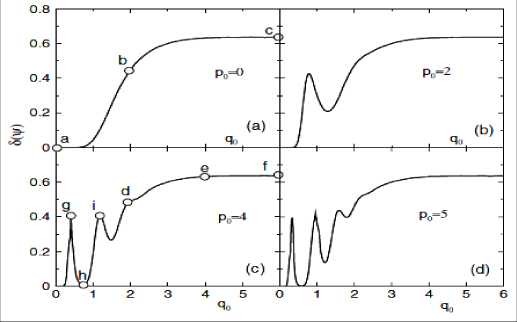
Рис. 17. Поведение индикатора неклассичности s для состояний

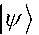
кота Шредингера в

зависимости от дистанции разделения состояний q и фиксированных значениях момента p

На рис. 18 приведено в графическом виде поведение функции Вигнера, при котором параметр 5 q достигает максимального значения.

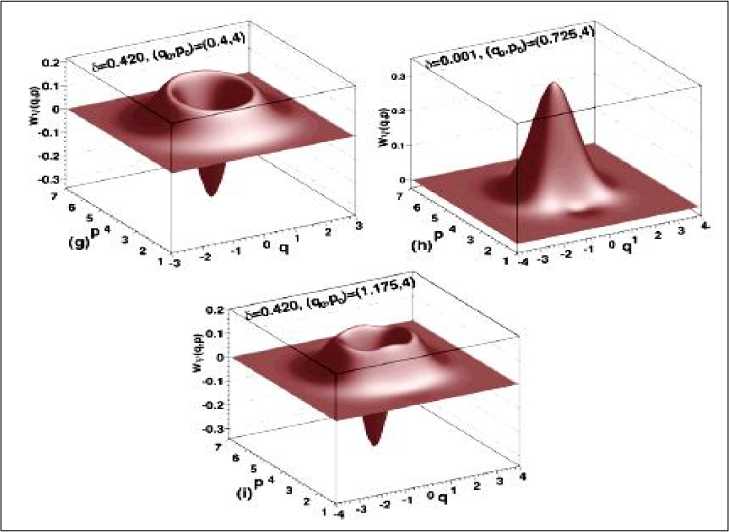
Рис. 18. Поведение функции Вигнера при значениях параметра p , при которых зависимость 5 q достигает максимального значения

Например, 6 при q ₀ 0.725 (рис. 18h) меньше по значению, чем при q 0.4 (рис. 18g) или 1.175 (рис. 18i). Это происходит вследствие несимметричности структуры интерференции по отношению к рефлексии параметра pp в противоположность к случаю состояний кота Шредингера при p 0 .

• - Физические аспекты отрицательного характера характер функции Вигнера . Поскольку функция Вигнера W ос не может быть проинтерпретирована как классическая функция распределения вероятностей, то было показано, что функция Вигнера ограничена снизу и сверху с нормировкой d ² W a = 1 . Было показано, что негативная часть функции Вигнера может рассматриваться как индикатор неклассических свойств. Так была определена мера неклассичности по объему нега-

  тивных частей распределения Вигнера в виде б = — J d ² W

  -                                        Q ⁶

  может быть нормализована согласно выражению У =—---

  
  

  а

  
  

  с

  
  

  |-Wа

  
  

  и

  
  

  целью иметь дело с мерой 9 ,

  
  

0      1, где нуль означает, что имеем классические состояния и единица означает состояния с

максимальным свойством неклассичности. Рассмотрим некоторые примеры.

-

Четное

когерентное состояние (even coherent state). В этом случае

21+ e ² W ²

IA+I-A и является суперпозицией двух когерентных состояний.

Функция Вигнера имеет вид⁸: W а =       ¹       e ^{2    2} e ^{2    2}  2 e ^{2 и} cos

2   ²

71 1 e

Из рис. 19 видно, что функция Вигнера имеет явно выраженную негативную часть в исходной позиции. Осцилляции, которые возрастают с увеличением сепаратриссы когерентности, являются следствием квантовой интерференции двух рассматриваемых когерентных состояний.

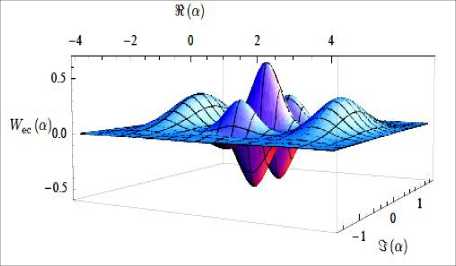
Рис. 19. Вид функции Вигнера для четного когерентного состояния _ec      0.25

Видно, что два когерентных пика локализованы в состояниях ОС = 2.5 и ос = -2.5 . Около исходного состояния функция Вигнера проявляет существенные осцилляции и принимает отрицательные значения. В силу осцилляционных свойств косинуса оценить аналитически интеграл негативной части функции Вигнера ¹ d ² W _ec а |- — трудно.

На рис.20 проиллюстрирована нормированная мера i9 | Р^ как функция от параметра Р сепаратриссы когерентности состояний, где интегрирование проведено численным методом.

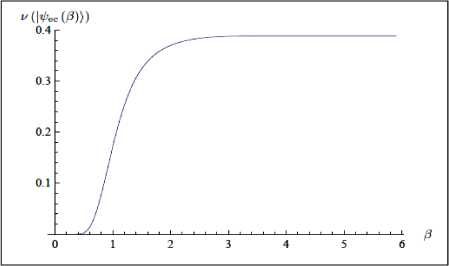
Рис. 20. Поведение нормированной меры неклассичности, основанной на негативных частях функции Вигнера для четного когерентного состояния

Для р - 0 имеем вакуумное состояние. Его функция Вигнера всюду положительна и поэтому i9 |00, т.е. не проявляет свойств неклассичности. С увеличением разделения, квантовые осцилляции возрастают, и мера i9 | if/ ec P ) также монотонно увеличивается до тех пор пока не достигнет своего предела ⁹ 1^^°°)+ *0.389 для достаточно больших значений p . Поведение меры <9 | p^ подтверждает интуитивное предположение, что свойство неклассичности возрастает с увеличением квантовых осцилляций и также с увеличением разделения когерентности. Рассмотрим одно важное состояние – состояние Фока.

• - Состояние Фока . Другим хорошо известным примером состояний с неклассичекими свойствами является состояние Фока вида 1^_F) = I n ¹ a € ^{† n} 0^с n 0,1,2, Его функция Вигнера n !

может быть вычислен в виде W1 n L 4  2 e2  , где Ln полиномы Лягерра n -го порядка.

На рис. 21 приведены графики поведения функции Вигнера для трех различных значений параметра n .

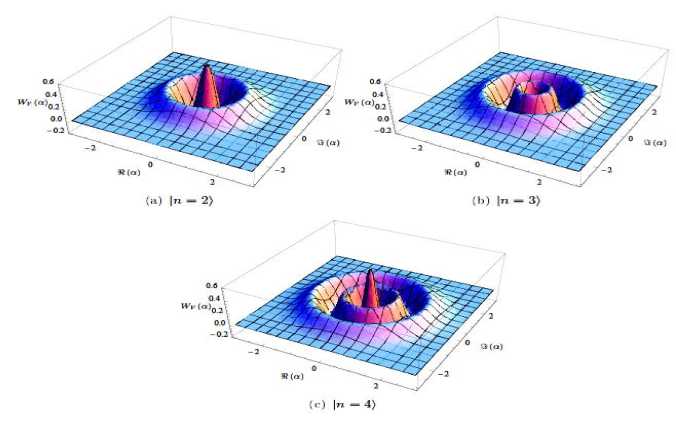
Рис. 21. Функция Вигнера для трех состояний Фока

С увеличением числа фотонов n осцилляции также увеличиваются и функция Вигнера приобретает явно выраженные отрицательные значения для всех n 1 .

Мера неклассичности б n может быть аппроксимирована в виде б I nn для 4

0 n 250 . Используя данную аппроксимацию на рис. 22 приведена нормированная мера неклассичности 9 n состояний Фока.

Мера неклассичности возрастает монотонно с увеличением числа фотонов и приближается к максимально возможному значению i9 I n —> 00 \ = 1. Отметим, что n как чистое состояние означает, что n фотонов контролируемы с нулевыми флуктуациями \ An 0. Состояние Фока с высоким числом фотонов не является классическим когерентным состоянием со средним значением (al n€ и = ы и вариацией (tz An€ 2 .

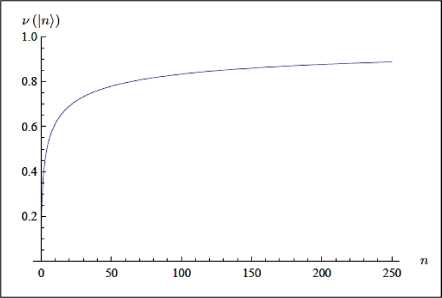
Рис. 22. Нормированная мера s n неклассичности, основанная на негативной части функции Вигнера для состояний Фока n как функции числа фотонов n

Этим объясняется поведение возрастания меры S n с увеличением числа фотонов.

-

Сжатое вакуумное состояние. Сжатый вакуум |^ ,0 ) определяется из вакуумного состояния применением унитарного оператора сжатия S g к вакууму как

Амплитуда r = 1^1 комплексного параметра сжатия ^ = re ⁱ играет роль мощности сжатия, тогда как угол 0 определения направления сжатия.

Сам термин сжатие отражает факт, что оператор S€ § приводит к редукции вариаций квадратуры компонент в направлении сжатия и последовательно к возрастанию вариаций в перпендикулярном направлении. Ниже показано, что сжатый вакуум является существенно неклассическим состоянием для

Тем не менее, его функция Вигнера

W _sq a

2 \a cosh r + ae ⁱ sinh r

71 L ^{1                                         1}

и как следует из рис. 23 нигде не принимает

отрицательного значения и поэтому i9 1 1[/     0^ ^ .

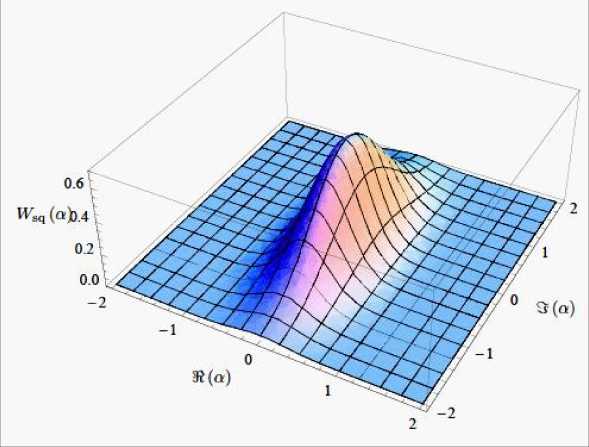
Рис. 23. Функция Вигнера для сжатого вакуума \^ ⁼ 0.5,0 )

• -    Влияние запутанных состояний на не классичность . Потенциал запутанных состояний рассматривается как возможный ресурс генерации неклассических состояний и является мерой неклас-сичности. Физически вычисление потенциала запутанных состояний требует знания оптимальных дополнительных состояний и линейных оптических преобразований, которые порождают две составляющие запутанных состояний.

Так распределение с€ с заданным состоянием линейного оптического плотности, порождающего запутанные состояния, состоит из дополнительного вакуумного входа и простого расцепления луча света (beam splitter - BS), приводящего к преобразованию состояния в виде:

с€ ^{U €} BS ^{с€ 00 U €†} BS ^.

Далее определяется специальная мера запутанных состояний в виде относительной энтропии запутанных состояний или т.н. потенциала энтропии запутанных состояний следующего вида: EEP с€  min Tr € log € log с€ . Для состояния Фока с€ nn мера ЕЕР вычисляется как с€ D       с2с2

EEP n х n   n 2 ²

n

n

k 0< ^k

log2

n k

и для состояния сжатого вакуума с€= 1^ = re ⁱ ,0х^,0

определятся как EEP 1^,0 ^ ,0I = cosh ^{2 r} log cosh ²

r

sinh ^{2 r} log  sinh ²

r

.

На рис. 24 показаны оба энтропийных потенциала как функции среднего числа фотонов n   a €^† a € .

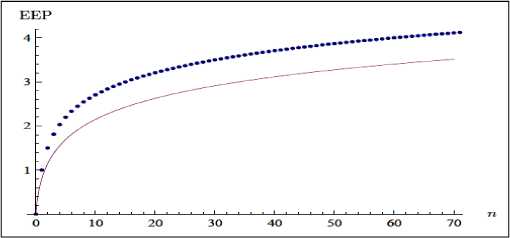
Рис. 24. Энтропийные потенциалы запутанных состояний для состояния Фока (пунктирная линия) и сжатого вакуумного состояния (сплошная линия) как функции среднего числа фотонов n   a €^† a €

Обе меры монотонно возрастают и расходятся в логарифмическом пределе при больших n . Данные специальные меры энтропийного потенциала показывают, что состояние Фока более неклассическое, чем сжатое вакуумное состояние.

Для примера на рис. 25 приведено сравнение функций Вигнера для сжатого вакуумного состояния, когерентного состояния и термодинамического состояния.

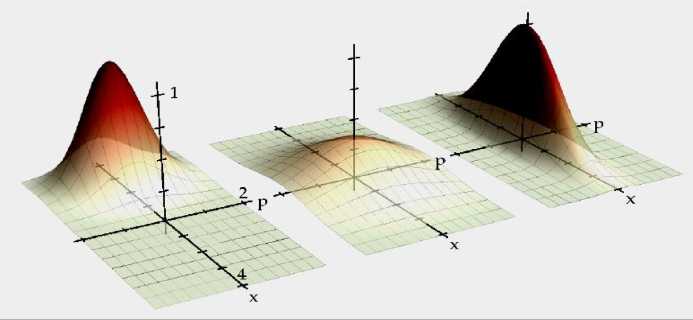
Рис. 25. Функции Вигнера для когерентного состояния с амплитудой 2 — -2 (слева), термодинамического состояния со средним значением числа фотонов nth    (среднее) и сжатого вакуумного состояния с уровнем сжатия r = ln2 (вариация сжатия 1/8) (справа)

• -    Состояния Фока для гармонического осциллятора . Полная концепция фотонов тесно связана с концепцией неклассичности состояний и это следует непосредственно из наличия отрицательных значений функции Вигнера. Для гармонического осциллятора x , p функция Вигнера имеет вид

• 1   ²²     n

W x , p     e ^p 1 L  2 x   2 p . Четное когерентное состояние имеет функцию Вигнера

л вид W 0, 0   1 /  . Для различных значений 1, 2 и 3-числа фотонов состояний Фока на рис. 26 при ведено поведение Вигнера.

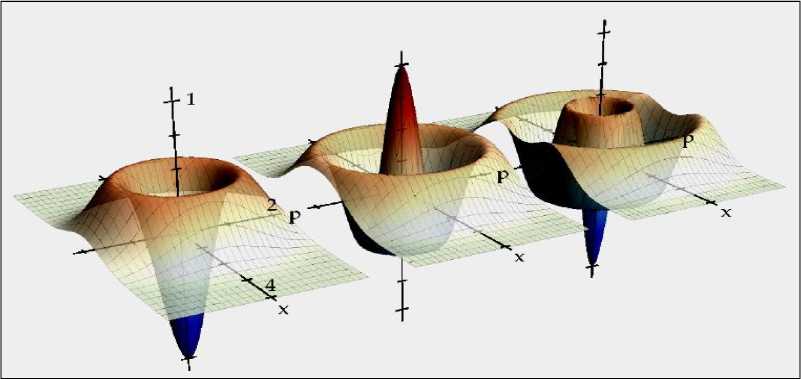
Рис. 26. Функция Вигнера для различных значений 1, 2 и 3-числа фотонов состояний Фока (слева направо)

Отметим, что в этом случае имеем альтернативное чередование отрицательных и положительных значений в основном состоянии.

• - Состояния кота Шредингера. В свете рассмотренного гармонического осциллятора рассмотрим состояние КШ N       eⁱ      , которое является суперпозицией двух когерентных состо

яний с противоположными фазами. Коэффициент N является нормирующим множителем. В специ- 38

альном случае, когда когерентный фактор eⁱ равен 1 или 1 , имеем четное и нечетное состояние кота Шредингера, соответственно. В функции Вигнера, имеющей вид

W x, p             W x 2 , p W x 2 , p   2W x, p cos 2 2 p ,

22 e ^{2    0              0                0}

которое содержит волнообразные паттерны с негативными составляющими между двумя Гауссовскими пиками что отображено на рис. 27.

Распределение числа фотонов состояний кота Шредингера (КШ) осциллирует между нечетным и четным числом фотонов. В частности, для нечетных и четных состояний кота, выражения для числа состояний имеют вид

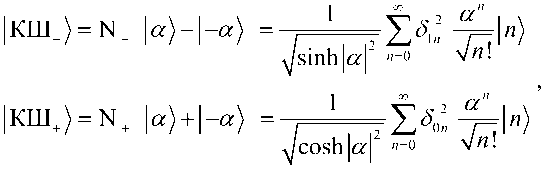
т.е., нечетные состояния кота содержат только нечетное число фотонов, тогда как только четное число фотонов содержится в четных состояниях кота.

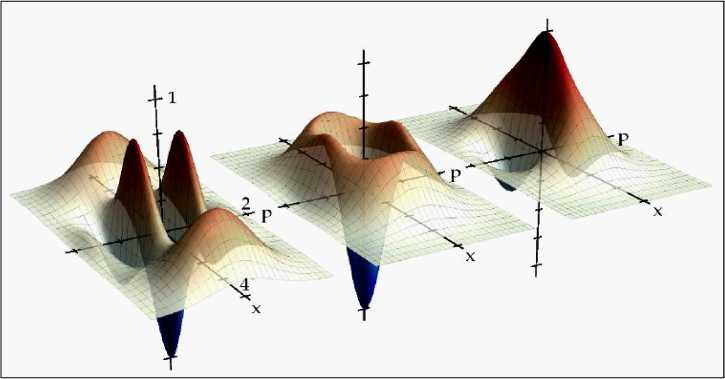
Рис. 27. Примеры функции Вигнера для состояний кота Шредингера или когерентных состояний суперпозиции (слева направо нечетные состояния при    2 , при    1 , и четное состояние при ос = 1 соответственно)

В приведенном выражении плюс и минус означает четные и нечетные состояния кота Шредингера, соответственно, и W ₀ x , p представляет вакуумную функцию Вигнера, параметр предполагается принимает реальные значения. Видно, что интерференция между пиками двух когерентных состояний при и    заметно изменяет вид с возрастающей амплитудой [28].

Экспериментальная проверка неклассических свойств состояний квантовой суперпозиции, запутанных состояний и интерференции

Рассмотрим некоторые экспериментальные результаты, подтверждающие наличие рассматриваемых физических эффектов и квантовых состояний с неклассическими свойства, имеющими отрицательные значения функции Вигнера.

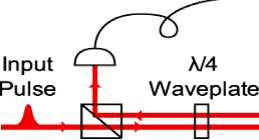
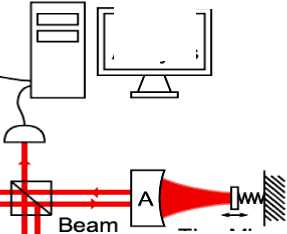
- Квантовая суперпозиция . Схема экспериментальной установки по проверке наличия состояния квантовой суперпозиции, воспроизводимого в микроскопической оптикомеханической системе⁹, представлена на рис. 28.

Single Photon Detectors (2)

Polarizing Beam Splitter

Data Analysis

Tiny Mirror/

Splitter M          Cantilever

Stationary Cavity

Рис. 28. Диаграмма проводимого эксперимента

Входной импульс (input pulse) расщепляется между двумя плечами интерферометра Микельсона, обозначенных на рис. 28 как А и В, состоящих из высокопробных оптических полостей. На конце полости в плече А закреплено микроскопическое зеркало, движение которого осуществляется под давлением от излучения света в полости. Каждый выход порта интерферометра регистрируется простым фотонным датчиком и результат анализируется на РС с целью вычисления меры прозрачности интерференции. Начальное состояние консоли рассматривается как когерентное состояние с комплексной амплитудой P , а полное начальное состояние определяется как w 0     1   0,1)   +11,0\.®|д)

2            n_a , n_b            n_a , n_b

с параметром оптикомеханической

связности k и

унитарным оператором эволюции

X

U t exp i CDtaa+ b b i ka a CD t sin CD t

kaiCDtit a 1 e i ct c 1 ei ct c exp -i CDcc ct

Под действием унитарного оператора (13) данное начальное незапутанное состояние осуществляет эволюцию в виде:

1                                                    ik CDct sin ct + ik Im 1 e ctI л \\

1^ t ¹ e ^{i at} 0,1^®l^ _e i c t ^ + _e ik   c t sin c t ik Im 1 e ^c _1,0)®l k 1 e ^ct ^p_e c ^t

2                                                                                  ;(14)

• ¹    e ^iat   0,1)®|ф            ik ² t sin t i Im     t t

Поскольку консоль смещается только тогда, когда фотон находится в плече А, то состояние фотона и состояние консоли образуют запутанное состояние. Поэтому выходной сигнал консоли образует суперпозиции двух когерентных состояний с зависящими от времени амплитудами Ф t, когда фотона нет и с амплитудой Ф t , когда фотон присутствует в консоли и пространственное расстояние между двумя состояниями |ф и |ф консоли определяется как Аx— v 8kx , а два e 2k2 .

состояния консоли имеют наименьшую огибающую |(Ф о I ^^ 1^| —

После полного периода механически колебаний оба состояния идентичны и поэтому состояния фотона и консоли не являются запутанными состояниями. Для демонстрации состояния квантовой суперпозиции требуется наименьшее значение огибающей с k ∙ 1 /  2 .

На практике мерой измерения является прозрачность интерферометра определяемой совместными измерениями двух простых фотонных детекторов. Данная прозрачность определяется как удвоенное абсолютное значение вне диагональных элементов редуцированной матрицы плотности фотонов 9 t exp |^— k ² 1 cos со t . Прозрачность можно непосредственно оценить через запутанные состояния между фотоном и консолью. Для чистого двух частичного состояния мерой супер-корреляции запутанных состояний можно определить в виде энтропии фон Неймана для фотона в терминах прозрачности 9 t (рис. 29) как:

„       ~                       3 t 1 t 1 2

S t Tr с_фотlog₂с_фот 1+      log₂                log₂ 1 -9 t ²   ,       (15)

2         1 t 2

где с задает редуцированную матрицу плотности фотонов.

На рис. 29 представлены графики поведения прозрачности и энтропии фон Неймана.

Так как для чистых состояний двух частичной системы высокому значению энтропии фон Неймана соответствует высокая корреляция запутанных состояний подсистем, то можно сделать вывод, что когда начальное состояние является чистым, то прозрачность является хорошей мерой для оценки неклассичности поведения консоли.

В эксперименте вычисляется функция Вигнера для безразмерных x и p для фотона с состоянием суперпозиции 0,1^ + eⁱ 1,0 ) для устранения возможности разрушения квантового состояния консоли, с которым фотон находится в состояниях суперкорреляции.

Изменение 0 смещает пики интерференции, но не изменяет вид функции Вигнера.

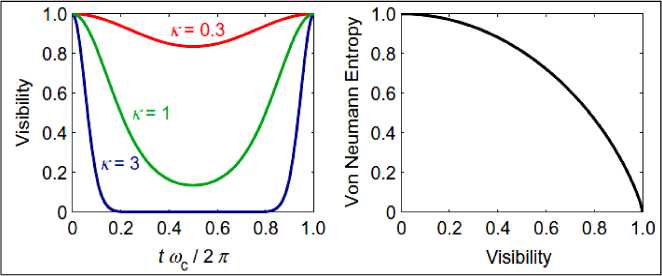
(а)                                   (б)

Рис. 29. Прозрачность 9 t как функция параметра оптикомеханической связности k (а) и энтропии фон Неймана St в терминах параметра прозрачности9 t (б)

На рис. 30 показан вид функции Вигнера для состояния консоли.

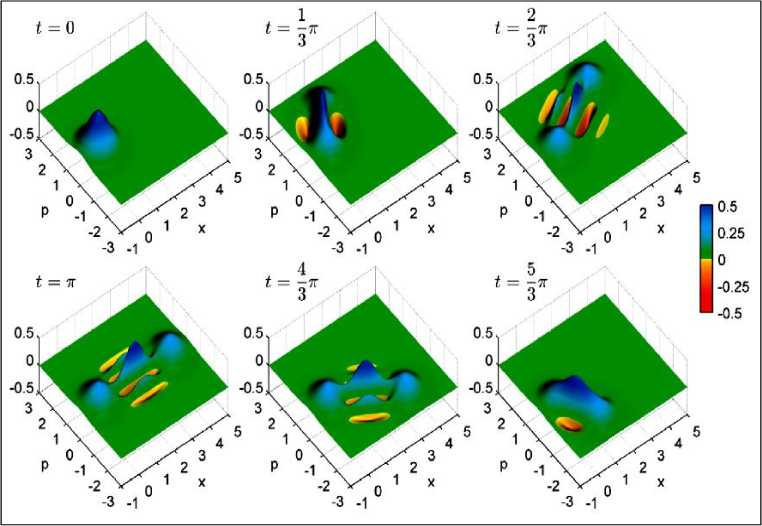
Рис. 30. Временная эволюция функции Вигнера для Р = 0, k = 2 и h — 1—т = 1

На рис. 30 области с отрицательными значениями функции Вигнера обозначены желтым и красным цветом, и соответствуют неклассическим состояниям консоли.

Из рис. 30 видно, что состояние системы периодически находится в состояниях с высоким уровнем неклассичности и отрицательными значениями функции Вигнера.

• - Запутанные состояния. Наряду с суперпозицией Шредингер ввел понятие запутанных состояний, которые применяют для описания состояний системы, состоящей из нескольких подсистем и пространственно разделенных и делокализованных.

На рис. 31 приведен пример10 таких состояний.

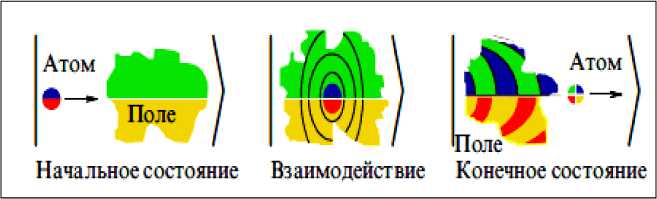
Рис. 31. Запутанные состояния в составной системе - двухуровневый атом и поле

Другой пример приведен на рис. 22 для запутанного состояния, образованного двумя однофотонными пучками с различающимися волновыми векторами.

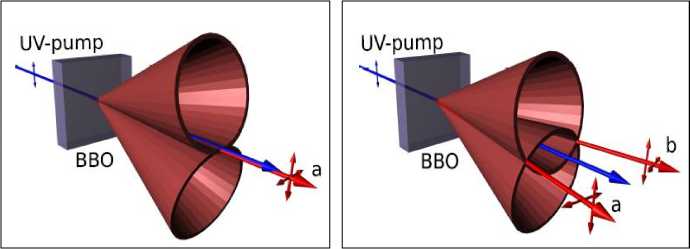
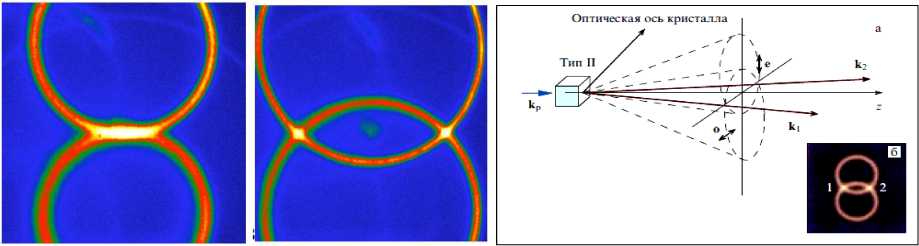
Рис. 32. Запутанные состояния

На рис. 32 атом пролетает область взаимодействия с полем резонатора. После короткого взаимодействия атом и поле оказываются пространственно разделенными. Однако состояние общей системы оказывается взаимозависимым, запутанным.

В результате поле жестко связано с сотоянием атома, а время жизни такого запутанного состояния 1^ = 1 атом поле + | атом поле может быть много больше времени взаимодействия. Каждое из зпутанных состояний обладает замечательным свойством: измерение одного из фотонов проецируется на состояние с определенной поляризацией и поляризация фотона из другого пучка становится также известной. При этом знание о состояни полной системы не гарантирует полного знания о состоянии составляющих подсистем.

Запутанные состояния пары фотонов получают при каскадных распадах в атомных системах и в параметрических процессах при резонансной флуоресценции, где фотоны со и CD , рожденные при рассеянии двух фотонов накачки 2 CD , находятся в запутанных состояниях.

Применение квадратичных кристаллов с фазовым синхронизмом II типа (см. рис. 22) позволяет получить поляризационно запутанных состояний в направления 1 и 2, определяемых пересечениями конусов синхронизма для обыкновенных и необыкновенных фотонов, создавая возможность формирования состояний типа Белла. Сохранение импульса внутри кристалла (т.н. «фазовый синхронизм») достигается благодаря двулучевому преломлению кристалла, позволяющего компенсировать дисперсию в кристалле. В результате сигнальные и холостые фотоны создают радугу цветных конусов, в которых сопряженные фотоны излучаются в противоположные стороны от пучка накачки.

В случае фазового синхронизма типа I сигнальные и холостые фотоны имеют одинаковую линейную поляризацию, перпендикулярную поляризации фотонов накачки, и их конусы концентричны с пучком накачки. В случае фазового синхронизма типа II сопряженные пары образуются из обычно (о) и необычно (е) поляризованных фотонов. В этом случае конусы сигнальных и холостых фотонов имеют различные оси. В случае одноосных кристаллов с отрицательной дисперсией ось конуса необычно поляризованных фотонов расположена между осью кристалла и пучками накачки, а ось конуса обычно поляризованных фотонов расположена дальше от пучка накачки (но оси и пучок накачки лежат в одной плоскости).

Приведенное на рис. 32 получается при фотографировании излучения, испускаемого нелинейным кристаллом при параметрическом распаде, перпендикулярно направлению накачки. В частности, цифрами 1 и 2 обозначены направления, в которых создаются поляризационно- коррелированные пары фотонов. В этих направлениях поляризация не определена, но поляризации должны быть различны. Рассмотрим пример манипулирования запутанными состояниями.

• -    Дистилляция запутанных состояний . Базовая концепция протокола и схема экспериментальной проверки дистилляции запутанных состояний представлены¹¹ на рис. 33а,б.

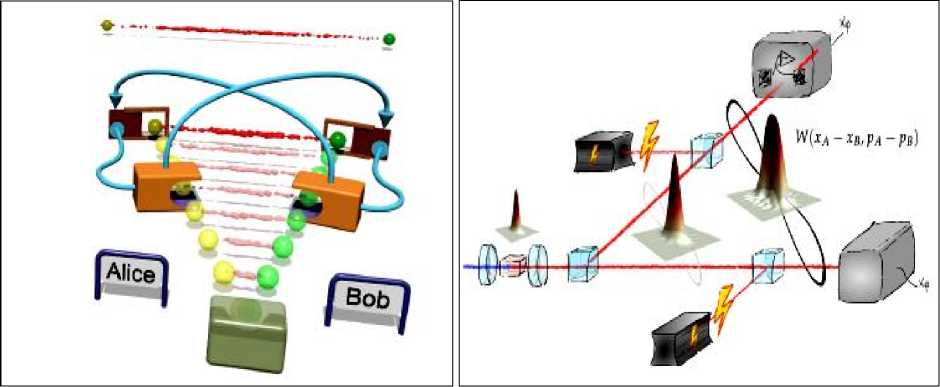
(а)                                                      (б)

Рис. 33. Концепция (а) и схема эксперимента (б) дистилляции запутанных состояний

Конечное запутанное состояние усиливается действием локальных вероятностных операторов (оранжевый цвет блока) с применением классической коммуникации (голубые соединения) для выбора суперкоррелированных пар (рис. 33а), которые можно успешно дистиллировать. Функции Вигнера могут показать измеримые и реконструированные состояния А - В составляющих, составляющие А + В находятся в вакууме.

Таким образом, основной идеей дистилляции запутанных состояний, как важнейшего информационного ресурса, является создание возможности приготовления Алисой и Бобом серии запутанных состояний с последующим применением к ней локальных операций. Потом с помощью каналов классической коммуникации определить какие из состояний могут успешно получить усиление супер-корреляции и могут в дальнейшем быть использованы в информационном процессе. Данный процесс применяется для повышения скорости разделения состояний и повышения числа запутанных состояний.

В эксперименте на рис. 33б воспроизводятся двухсоставные составляющие запутанных состояний в сжатом состоянии вакуума в 50 : 50 расщепители лучей. Это дает возможность порождать состояние с достаточно конечным уровнем супер-корреляции, эквивалентное ЭПР парам сжатых состояний. Для реализации локальных операций используется техника извлечения фотонов и определяется результирующее квантовое состояние. Для описания запутанных состояний до и после дистилляции реконструируется взаимная двухкомпонентная матрица плотности состояний путем гомодинного детектирования обоих выходных компонент для недистиллированного состояния и для состояния с одновременно извлеченным фотоном для каждой из двух компонент. Результат дистилляции показан на рис. 34а.

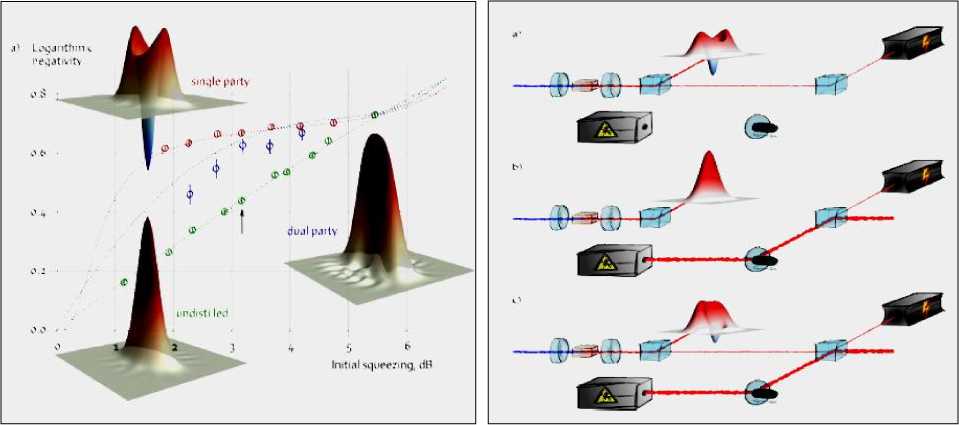
(а)                                                         (б)

Рис. 34. Логарифмическая отрицательность недистиллированного и дистиллированного состояний для различных уровней сжатия состояний (а) и воспроизведение состояний кота Шредингера

В качестве меры супер-корреляции запутанного состояния использовалась логарифмическая отрицательность, которая нетрудно вычисляется через знание матрицы плотности. Воспроизведенные состояния образуют суперпозиции сжатых состояний вакуума и представлены на рис. 34б, а на рис. 35 представлена полная серия воспроизведения состояния кубита.

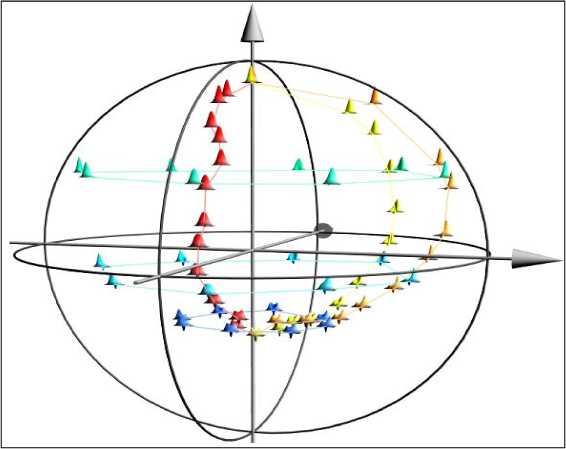
Рис. 35. Сфера Блоха с экспериментальными и реконструированными состояниями кубита с описанием состояний функцией Вигнера (северному полюсу соответствует сжатое состояние

S ^€ r 0 и южному полюсу - S r Ц с r = 0.38 )

• -    Дистанционное управление генерацией гибридных запутанных состояний между волновыми и корпускулярными свойствами оптических кубитов . Дуализм волновых – корпускулярных свойств приводит к двум разным способам и схемам кодирования в оптических системах обработки информации. В рассматриваемом подходе¹² при первом измерении воспроизводится генерирование запутанных состояний между оптическими кубитами этих различных типов, затем локализуются и объ-

• единяются путем коммуникации через каналы связи без потерь. Такие гибридные запутанные состояния являются ключевым ресурсом во многих информационных процессах обработки данных, включая квантовую криптографию и квантовые вычисления, при конвертировании информации из одного Гильбертова пространства в другие пространства путем телепортации состояний и поэтому позволяет дистанционно осуществить взаимодействие квантовых процессоров, основанных на различных способах кодирования.

Оптическая схема такого способа показана на рис. 36.

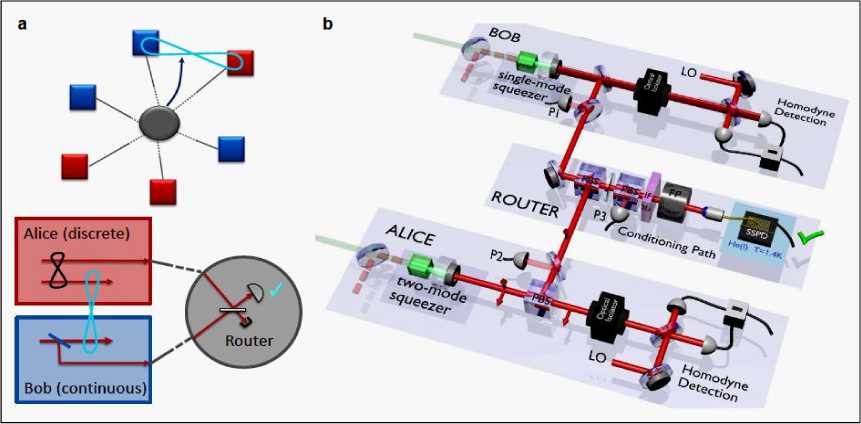
Рис. 36. Воспроизведение гибридных запутанных состояний на основе измерений:

• (а) схема эксперимента; (в) схема реализации эксперимента

Алиса и Боб для формирования гибридных запутанных состояний используют дискретные и непрерывные переменные соответственно. Приготавливаются два локальных неклассических оптических поля: двухкомпонентное сжатое состояние вблизи положения Алисы в виде I ^ ⁼ 10 ’ 0_Z) ⁺ ^ 11 ^?1) + O ^ , где сигнал ( ^s ) и холостая ( i ) компоненты, и нечетное состояние кота Шредингера на стороне Боба в виде КШ . Небольшая часть состояния кота

Шредингера отделяется и передается на делитель, где с неразличимой холостой компонентой состояния Алисы на выходе делителя светового потока формируется суперпозиция.

Результирующее состояние является запутанным с максимальной корреляцией и может быть записано как И AB = 10 а 1 КШ ) ,+= ”11) A ^КШ + ) в ■ где относительная фаза контролируемых триггерных компонент и КШ означает четное состояние кота Шредингера.

Конечное запутанное состояние можно переписать, применяя вращающийся базис кубита Алисы |+) = 10) + |1) /V2, |—)= |0) —11) Л/2 в виде: |^)AB = |+)A |a)B A-ei |-)A |a)B. Данное состоя- ние можно телепортировать из кубита, кодированного в базисе     ,    , в когерентное состояние с вычислительным базисом |a^,|— а^ , что отвечает принципу формирования кота Шредингера, когда два классических состояния образуют запутанное состояние с микроскопической степенью свободы. С помощью матрицы преобразования Адамара можно перевести данное состояние в состоя

ние I0)aI")b+ I1)а\-“\ •

Результаты эксперимента представлены на рис. 37.

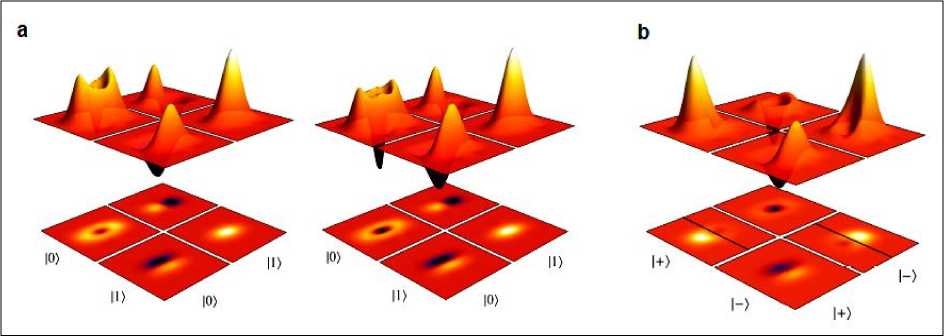
(а)                                      (б)

Рис. 37. Томография квантового состояния по экспериментальным данным

• (а) - функция Вигнера с редуцированной матрицей плотности kk | С^ / ^, k , / е 0,1 с / без коррекции потери измерения; (б) - функция Вигнера с редуцированной матрицей плотности kk |<€ / ^, k , / е +, — с коррекцией потери измерения

Сгенерированное состояние можно представить применяя вращающийся базис |+)= 10) + Ц /А|-) = |0)-Ц /V2  (рис. 37б). Из контура на плоскости видно, что две проекции    с€ и    с€ образуют противоположные смещения в фазовом пространстве и соответствуют максимальной величине соответствия (fidelity) по отношению к состояниям     и

| —а^ : fidelity = 77 + 3% по отношение к требуемому состоянию при ф — л и |а| = 0.9 .

На рис. 38 приведен пример результатов эксперимента для состояний с ф — Q , т.е. противоположного состояния по отношению к результатам на рис. 37.

Значение меры негативности N вычислялась для каждого сгенерированного состояния и показывает переход из разделенного состояния в запутанное состояние с максимальной суперкорреляцией и обратно.

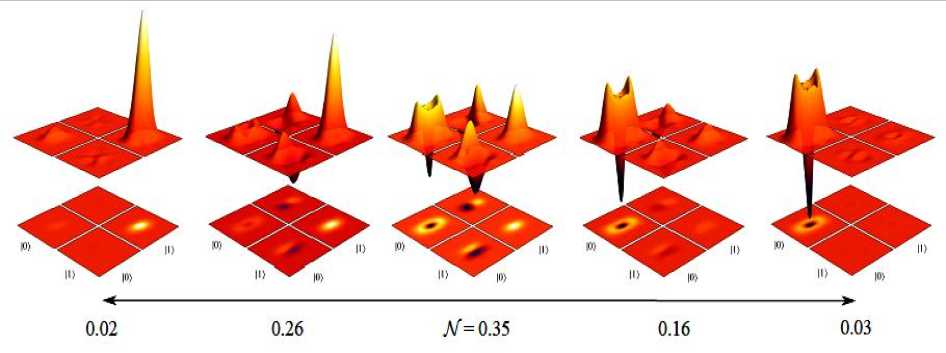
Рис. 38. Квантовые состояния с разделенным запутанным состоянием с максимальной суперкорреляцией (функция Вигнера с редуцированной матрицей плотности kk | <€ / ^, k , / е 0,1 )

Таким образом, имеется возможность дистанционно управлять формированием запутанных состояний с различными формами кодирования информации как с дискретными, так и с непрерывными переменными.

- Квантовая интерференция . На рис. 39 представлен общий вид эволюции плотности распределения вероятностей лучей при распространении от источника света к экрану ¹³.

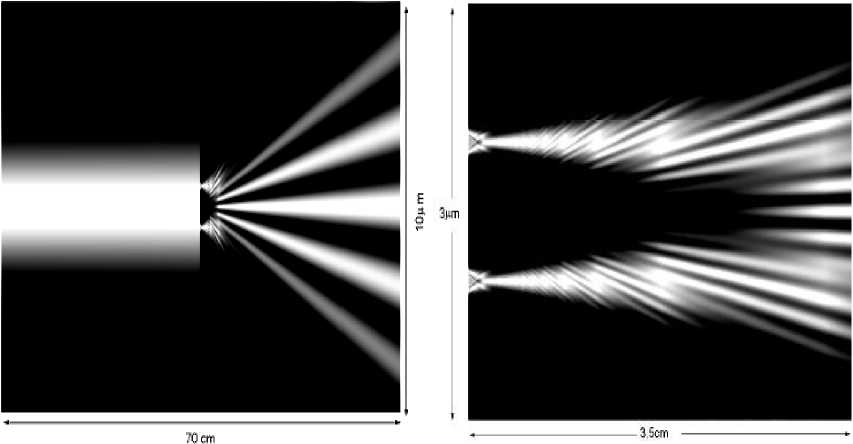
(б)

(а)

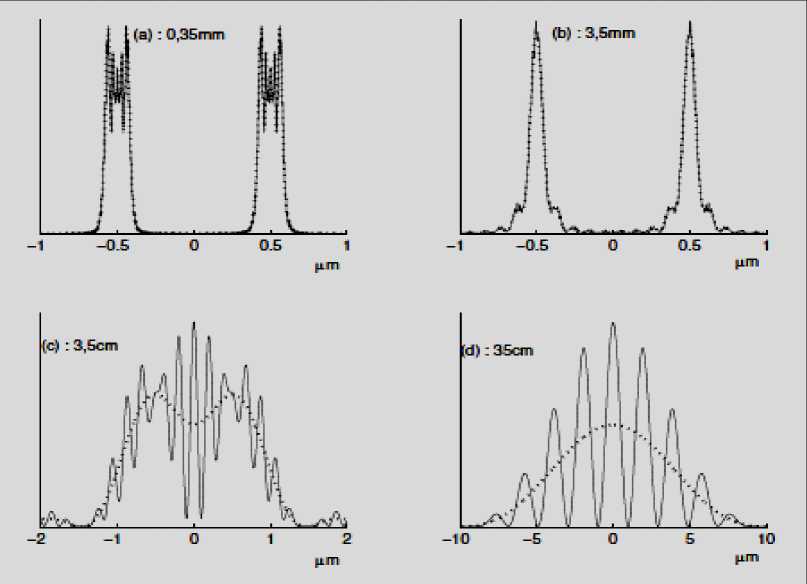
(в)

Рис. 39. Экспериментальные результаты формирования квантовой интерференции: (а) - общий вид эволюции плотности распределения вероятностей от источника света на экране в эксперименте

Джонсона (светлый фон отражает высокую вероятность); (б) - поведение плотности распределения вероятностей на расстоянии 3 см от щелей; (в) - сравнение плотности распределения вероятностей 1^AB2 (сплошная линия) с 1^AB2 (пунктирная линия) для различных значений расстояния от щелей: (а) 0.35 мм; (в) 3.5 мм; (с) 3.5 см; (д) 35 см

Вычисления осуществлялись на основе метода интеграла путей Фейнмана. Волновая функция до прохождения лучей щелей эквивалентна для     t t d /УП 2.10 11сек     как y,t     2Лs2 t e y -3t /4 ° 0s0t , где s0 t = а 1+i ftt /2mа2.

Так как ht /2 mо ²□ 1 , то волновая функция сохраняет свой гауссовский вид до прохождения щелей. Волновая функция после прохождения щелей t t t +d /SD 4.10 ¹¹ сек складывается из значений волновых функций после прохождения щелей А и В как у/ y , t = 1/J _A y , t _B y , t , где

^_A   y , t       K  y , t , y _a , t ₁      y _a , t ₁   dy _a ,     _B   y , t       K y , t , y _b , t ₁ ^ y _b , t ₁   dy _b

AB

K                                   4-    2 im y y ² /2/? t t ₁

y , t , y , t      m /2 i t e^{m y y}          .

Экспериментальные результаты, представленные на рис. 39, позволяют сравнить эволюцию плотности распределения вероятностей для различных расстояний от щелей (0.35 мм, 3.5 мм, 3.5 см, и 35 см): 1) при условии, когда две щели А и В открыты одновременно (явление интерференции амплитуд вероятностей 1^ AB ² ), и 2) когда щели А и В открывались независимо (сумма двух дифракций: 1^ A ² B ² ).

Результаты на рис. 39 достоверно подтверждают наличие квантовой интерференции амплитуд вероятностей независимо от интерпретации в теории Луи де Бройля-Бома (независимо относительно от положения квантовой частицы).

Таким образом, все конструируемые алгоритмически квантовые операторы квантовых алгоритмов имеют экспериментально подтвержденные физические модели, воспроизводимые устойчиво в реальных лабораторных условиях.