Квантовая релятивистская информатика. Ч. 3: применение решений квантовых волновых уравнений в квантовой информатике

Изучение квантовых эффектов в сверхтонких полупроводниковых гетероструктурах, как одной из основ аппаратной реализации устройств квантовой информатики, дало толчок появлению нового класса полупроводниковых приборов – резонансных туннельных диодов (РТД) и транзисторов (РТТ), обладающих высоким быстродействием (предельные частоты 10 ¹² Гц). Обсуждаются также широко проблемы создания квантовых интегральных схем и квантового компьютера, основными элементами которых станут квантовые точки, квантовые проводники, квантовые ямы, транзисторные структуры на основе квантовых размерных эффектов и устройств с управляемой интерференцией электронов. Основу развивающейся наноэлектроники составляют структуры, состоящие из чередующихся полупроводниковых слоев с различными электрофизическими характеристиками.

Наиболее часто для описания электронных свойств многослойных структур используют метод огибающих волновых функций, в котором в области каждого слоя влияние его периодического потенциала сводится к подстановке в оператор кинетической энергии эффективной массы, а изменения законов дисперсии на гетерограницах играют роль эффективных потенциалов.

Поэтому многие задачи оценки особенностей энергетического спектра и исследования движения частиц сводятся к исследованию поведения частиц в системах с различными видами потенциальных барьеров.

Примеры решений нелинейных уравнений Шредингера

Рассмотрим ниже некоторые особенности поведения простейших квантовых систем в разных видах потенциальных барьеров и их принципиальное отличие от поведения классических систем. Удобнее всего это сравнение начинать с примеров исследования динамического поведения классического и квантового осцилляторов в заданном потенциальном поле

Пример 1 : Волновые гауссовские пакеты осцилляций квантового гармонического осциллятора . Для гармонического осциллятора уравнение Шредингера имеет аналитическое решение. Волновую функцию в общем виде можно представить как:

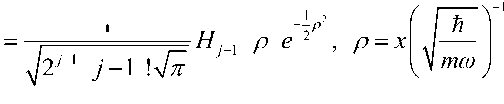
в терминах полиномов Эрмита H _{j 1} р . Например,

H 1, H 2 р , H 2 +4 р ², H ₄    12   8 ³ и т.д.

Для волновой функции 6     гармонического осциллятора на рис. 1,а показан график в терминах смещения        размерности      / m . Используя зависимость энергии

_ ho

E j 2j

2j1 , где j соответствует номеру уровня волновой функции, на рис. 1,б приведен график зависимости 20-го уровня энергии волновой функции гармонического осциллятора (2 20 1 39). Вертикальные линии показывают классические ограничения на энергию классического осциллятора, за который может выходить квантовый осциллятор.

Волновой пакет осцилляций квантового гармонического осциллятора определяется как суперпозиция волновых функций энергетических уровней в общем виде как         N  g jj    , с

j взвешенными весами g и постоянной нормирования N1/    g2 .

j

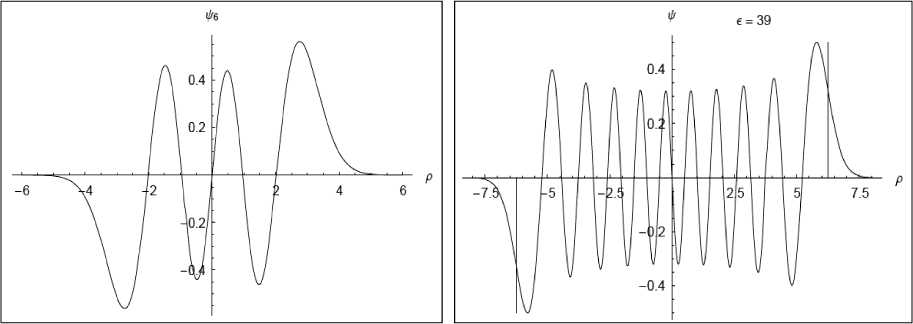
(а)

(б)

Рис. 1. Вид волновой функции ф6 р (а) и волновой функции 20-го энергетического уровня (б)

Например, волновой пакет можно сформировать из волновых функций для j 1,2,3 с относительными весами 25%, 50% и 25% в виде:

1             0.25 1       0.5  2       0.25 3

0.252  0.52

j         k djk,

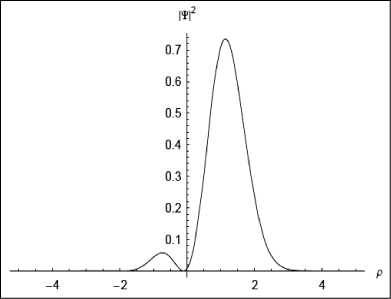
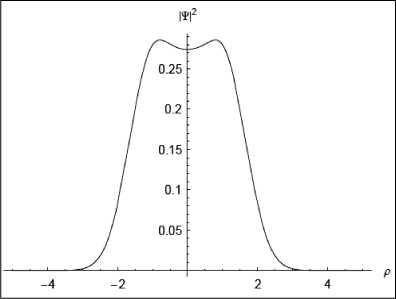
Плотность распределения вероятностей как квадрат от волнового пакета имеет вид, представленный на рис. 2, а.

Для описания движения волнового пакета во времени необходимо добавить к компонентам волновых функций зависящие от времени фазовые факторы в виде iEt/          i 2j 1t/          i

ej e2           e

t

.

Здесь использована зависимость энергии E, 2 j1 и j соответствует номер уровня волновой функции. Тогда для рассматриваемого варианта сумма от произведений данных факторов компонент волновых функций с взвешенными весами при умножении на коэффициент нормирования имеет вид:

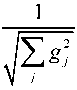
i g1  1      e

ti g2  2     e

ti g3  3     e

. При t 0 волновой

пакет     ,0 идентичен независимому от времени волновому пакету       и имеет одинаковую плотность распределения вероятностей (см. рис. 2, а).

(а)

(б)

(в)

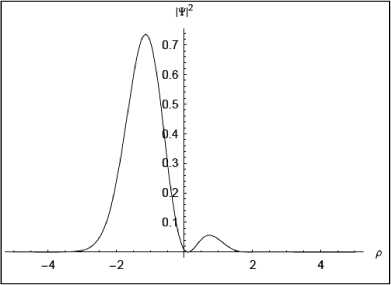
Рис. 2. Плотность распределения ^ р |² для трех компонент волнового пакета Т р

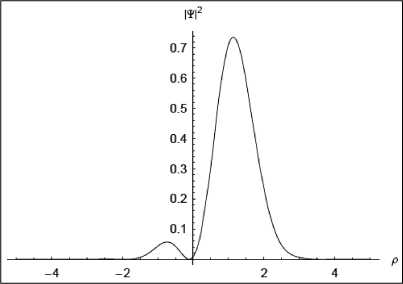
(г)

На рис. 2, б представлена плотность распределения вероятностей (квадрат от функции волнового пакета) для момента времени t = 0.25 / и , где скорость и = 2л / со , соответствующее четвертой части периода осцилляции волнового пакета. На рис. 2, в представлен вид функции плотности распределения вероятностей для полупериода осцилляций волнового пакета при t = 0.5 / и . И окончательно, после периода осцилляций при t = 1 / и функция плотности распределения вероятностей имеет вид, представленный на рис. 2,г. Нетрудно заметить, волновой пакет возвращается в исходную форму и локализуется в момент времени t = 1/ и .

Таким образом, общий вид зависящего от времени волнового пакета гармонического

1                               2 t осциллятора можно записать в виде: Ч7 /?,t = f -/^g^ Р е       • gk )

k

Данный пакет нормирован на 1 и функция плотности распределения вероятностей ^ р, t | осциллирует с периодом 1/и. Теперь можно спроектировать волновой пакет необходимого вида путем выбора значений соответствующих весов g . Экспериментально значения данных весовых коэффициентов определяются из состояния осциллятора в когерентной суперпозиции волновых функций j    . При этом когерентность означает определенное фазовое соотношение между волновыми компонентами пакета. Одним из общих результатов является гауссовское распределение весовых коэффициентов в суперпозиции состояния гармонического осциллятора.

На рис. 3, а представлен гауссовский волновой пакет, состоящий из 13 волновых функций _j    гармонического осциллятора после одного периода колебаний.

(а)                                     (б)                                 (в)

Рис. 3. Гауссовский волновой пакет, состоящий из 13 волновых функций ^_jр гармонического осциллятора после одного периода колебаний (а); для j 27 (б) и для j 47 (в)

Аналогично на рис. 3,б представлен график волнового пакета, состоящего из 13 волновых функций ^_jр гармонического осциллятора с индексом j 27 и на рис. 3,в – для j 47 .

Рассмотрим теперь вопрос о влиянии на зависимость от числа компонент волнового пакета на локализацию плотности распределения вероятностей.

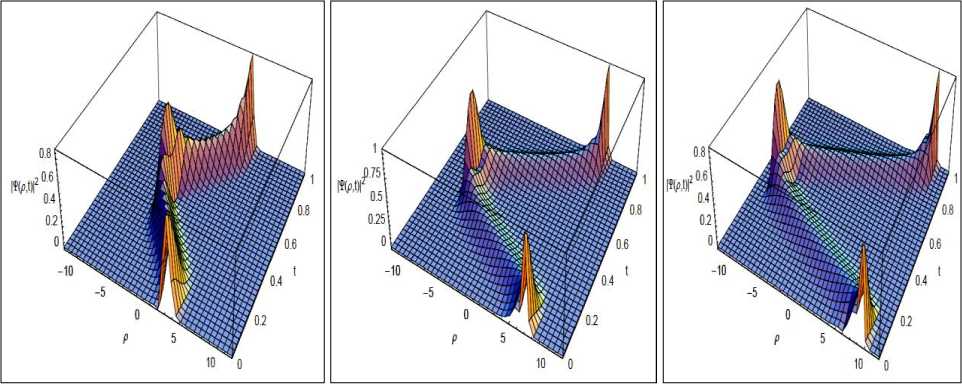
На рис. 4 показана динамика локализации плотности распределения гауссовского волнового пакета для каждой четверти периода 1/ и осцилляций гармонического осциллятора в зависимости от компонент в виде 5, 13 и 21 числа составляющих суперпозицию волнового пакета и j 30 .

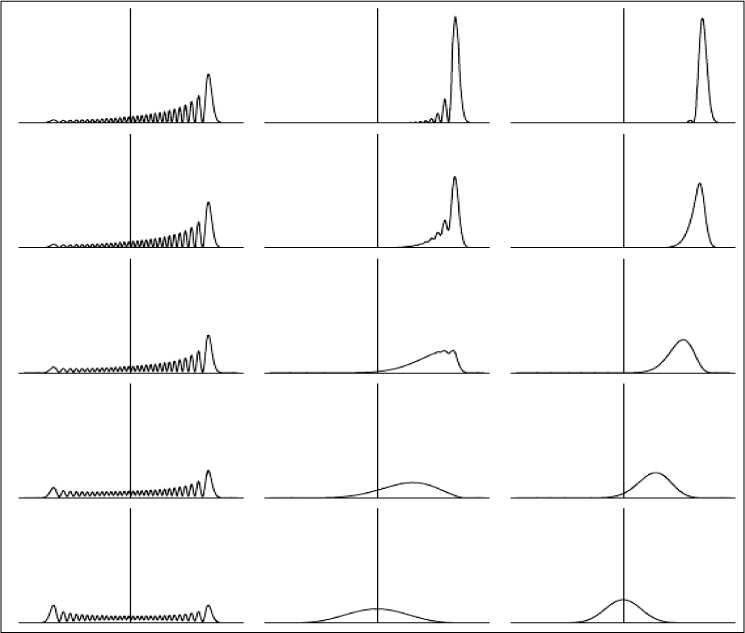
Рис. 4. Локализация плотности распределения гауссовского волнового пакета

На рис. 4 левый столбец соответствует 5-компонентному волновому пакету; средний столбец соответствует 13-компонентному волновому пакету; и правый столбец соответствует 21компонентному волновому пакету [1, 2].

Из результатов, приведенных на рис. 4 видно, что добавление большего числа компонент локализуют плотность распределения вероятностей в малой области аргумента для полного периода осцилляций гармонического осциллятора.

Рассмотрим еще одну особенность простого квантового осциллятора, которая отсутствует в классическом варианте.

Пример 2: Рассмотрим, следуя [3] свободный квантовый осциллятор, описываемый уравнением

Шредингера в виде:

2

i

t2 x2

Bx при условии x, 0 Ai      , где В – постоянная, Ai – функция Эйри. Решение уравнения (1) с

3/2

Bx заданным начальным условием x, 0 Ai       имеет вид [3]:

3/2

x, t Ai

B

2/3

B3t2 x

4m

exp

iB3t

2m

B3t2 x

6m

.

В интегральном представлении функции Эйри (2) можно представить в виде [3]:

2/3                     ik2t2

x, t           exp i kxdk

2 B            2m3

Из (2) следует, что ² не расплывается и равноускоренно движется в виде не расплывающегося волнового пакета со скоростью B ³ t ² /2 m ² . Такое, парадоксальное на первый взгляд, решение имеет глубокую связь с принципами симметрии волновых уравнений.

На рис. 5 показаны решения и экспериментальные результаты ¹ электронных лучей Эйри с самоускорением.

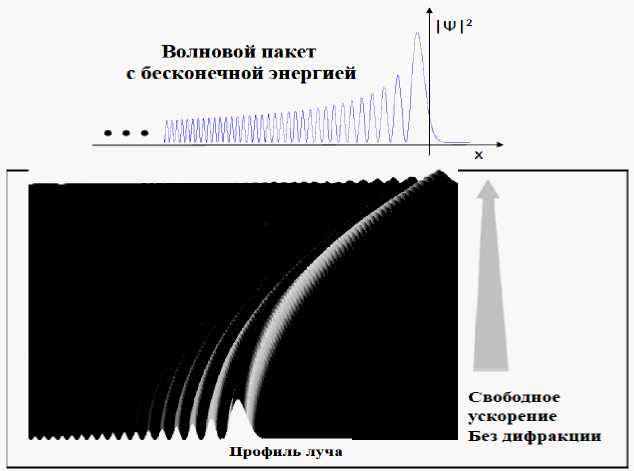
(а)

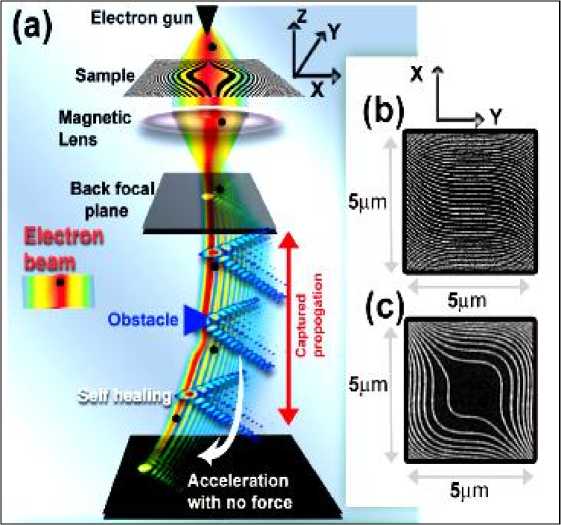
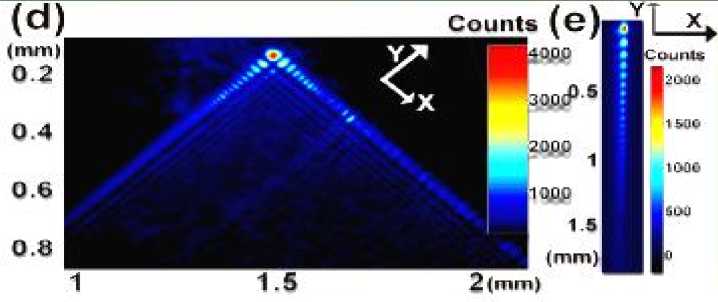
(б)

Рис. 5. Волновой пакет Эйри (а) и экспериментальная проверка самоускорения электронных лучей Эйри (б)

Новые решения ^2,3 показали существование отдельных пиков в плотности распределения вероятностей, которые ускоряются со временем. При этом данные решения можно получить как частный случай преобразований Нидерера ⁴ .

Типовые схемы квантовых резонаторов ^{5, 6, 7, 8, 9, 10} показаны на рис. 6.

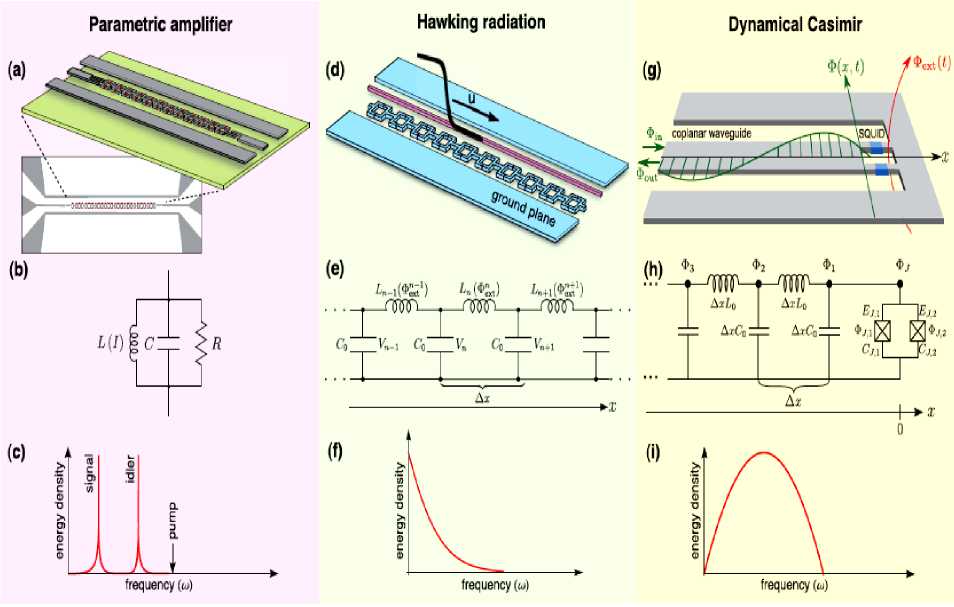
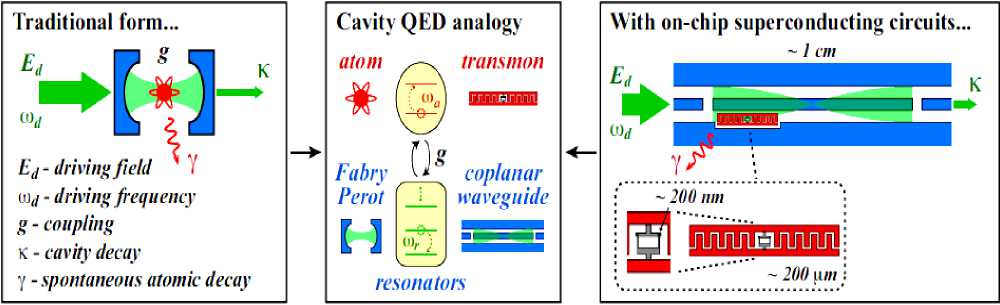
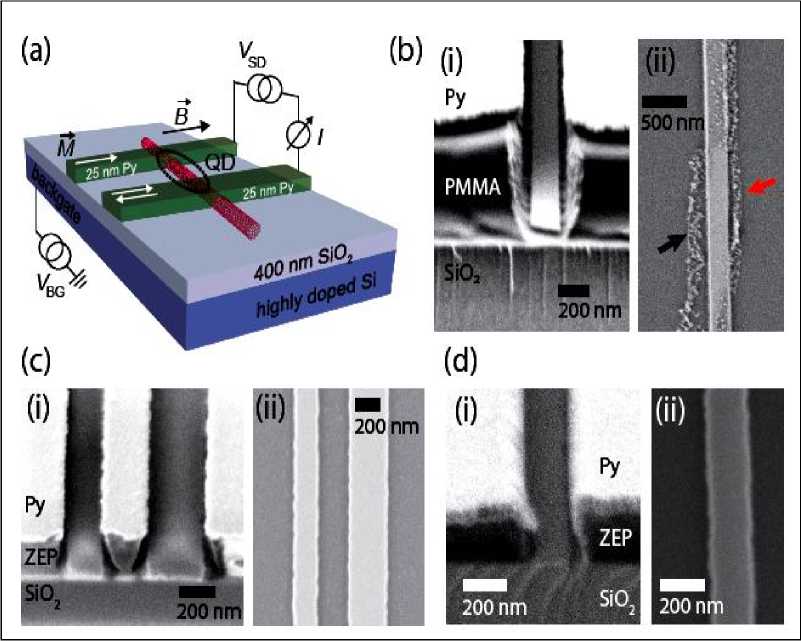
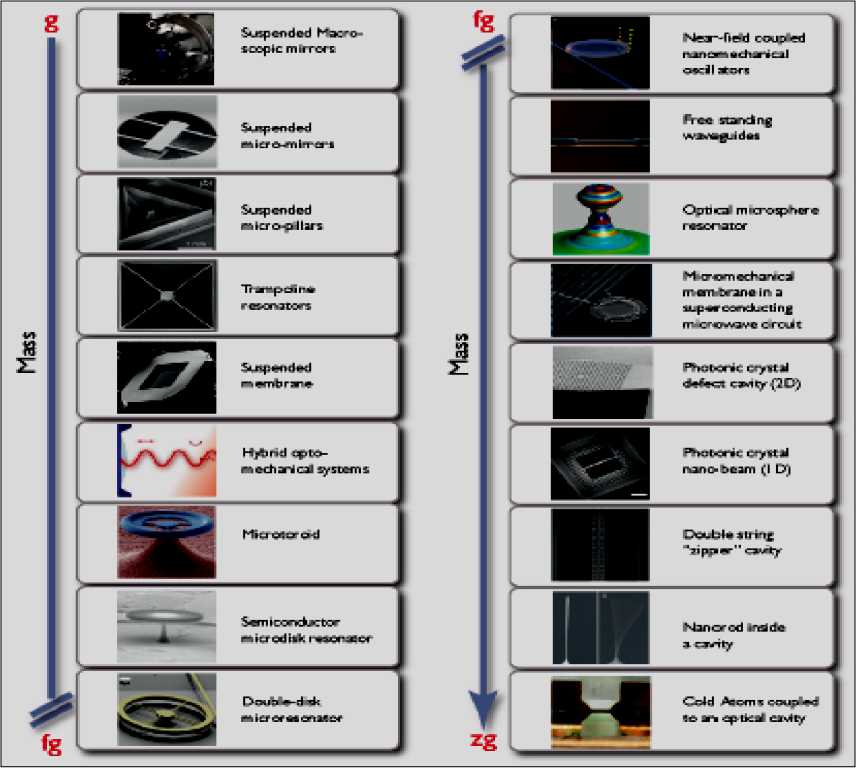
Рис. 6. Типовые схемы квантовых резонаторов и эквивалентные схемы

В [4, 5] показано экспериментально, что механический пьезоэлектрический резонатор с частотой 6 Ггц может долго находится в основном квантовом состоянии и демонстрирует неклассическое поведение в квантовом пределе.

Рассмотрим некоторые особенности и интересные для теории управления результаты моделирования нелинейных квантовых динамических систем с перекрестными связями. Интерес к решению задач оптимального управления квантовыми динамическими системами продиктован, в первую очередь, бурным развитием прикладных задач, в частности необходимостью разработки элементной базы микро – и наноэлектроники для систем управления и вычислительной техники, новых квантовых релятивистских ИТ, интеллектуальных наноматериалов и мн. др.

Основные результаты по оптимальному управлению квантово-механическими процессами ограничиваются в основном исследованиями моделей, описываемых уравнением Шредингера и его разновидностей. Поэтому отметим, в первую очередь, ряд математических моделей, описываемых нелинейными уравнениями Шредингера и некоторые особенности моделирования динамического поведения исследуемого класса объектов управления.

Примеры и решения уравнения Шредингера со сложными потенциалами

Типовыми моделями нерелятивистских квантовых систем, описываемых нелинейными уравнениями Шредингера, являются:

• x, t                                p-1

i --i-A^< x,t + ^ x,t    ip x,t =0, p >1,                 (4)

. бу x, t                M zj i ---------+ А у/ x, t + >     j—I ^ x, t at              j1xx

,6y x, t i at

My x , t

R ³

dy w x , t 0,

R ³

dy w x , t 0 .

Уравнение (4) относится к нелинейностями в пространстве

классу

_RR 3 _;

нелинейных уравнений Шредингера с локальными уравнение (5) относится к классу нестационарных

уравнений типа Хартри в RR ³ ,   x ₁ ,, x _M  - точки в R ³ , z – положительные константы; и (6)

описывает нестационарное уравнение Пекара-Шоке.

Разновидностью (4) – (6) является уравнение следующего вида:

,6y x, t i at

+ Ay/ x , t +Vx у/ x , t +

jy y , t I ² f x y dy к x , t   0 ,   (7)

R ³

где V E L^p R^N + _L q _R N _,

^N p , q < oo , f E L R^N +L⁶ R^N . Комплексно-значимое решение

типа у/ x , t   u x exp iXt , X g R при начальных условиях у/ x ,0     ₀ x приводит из (4) – (6)

к следующим уравнениям:

p 1               ^{M    z}

-Au+ X u  u p 1 u; -Au -^   j j1 x

u+ Xu+ |u ²

u 0;

-A u+ Xu   u ²

u 0 ,

соответственно. По комплексно-значимой функции u EL2R 3   определяется устойчивость орбитальных решений уравнений (4) – (6) при различных предположениях.

В табл. 1 приведены типовые формы нелинейных уравнений Шредингера и соответствующие условия нормировки, накладываемые на решение у/ x , t .

Таблица 1. Виды нелинейных уравнений Шредингера и условия нормировки решения

№	Уравнение динамики	Условия нормировки
1	2 iVУ t 2 m	2 d 3 x 1
2	2                   2 Я ™      ^ v t 2 m	2 d 3 x 1
3	ih4     2 Л^ + VУ^U м 2 оt 2 m	2 d 3 x 1
4	22 iVУ \ оt 2 m	4 d 3 x 1
5	it 2 m          V   *	4 d 3 x 1

Отметим, что в пп. 4 и 5 табл. 1 нормирование осуществляется со степенью 4 для плотности распределения вероятностей.

Допустим теперь, что имеются две невзаимодействующие системы  V1, 2 с координатами r1, r2. Если волновые функции у/1 r1, t ,^2 r2 , t   описываются уравнениями:

i й—— krk , t

5 t

й2

А + U r_k , t + Fk к k ² 2 m

^ _k r_k , t , k 1,2 ,

то, согласно постулату о сепарабельности, для произведения ^₁₂ имеем следующее уравнение:

^ у/ r,t r,t i    11   22

t

h 22

--А,--А, + U r , t +U r , t +F 1^   ²

_{2 m} 1    _{2 m} 2     1  1        2  2        12    1  2

V 1 ^r 1 ^{, t} V ₂ r ₂, t   (9)

Таким образом, из (9) следует условие в виде функционального уравнения: F 1 р 1    F 2 р 2     ^F 12 р 1 р 2 •

Обобщенным решением функционального уравнения (10) является

F Р =~b ln Рa ₁ , F ₂ Р =-b ln Рa ₂ , F ₁₂ Р =-b ln Рa ₁ a ₂ ,   (11)

где b

–

универсальная постоянная (размерности в энергетических единицах); a , a

–

действительные постоянные.

Уравнение, удовлетворяющее описанным условиям, имеет вид:

. 01// r , t i й-------- 5 t

й 2

д+ U r , t  b ln и² aⁿ  Fkk ²

V r , t .

Если уравнение (12) имеет вид ^ r , t , то 061// r , t exp ihbt ln |б^| также является решением уравнения (12).

Рассмотрим некоторые особенности решений нелинейного уравнения Шредингера с логарифмической нелинейностью, как частный случай (12) и имеющий большое применение в исследовании процессов в ионных ловушках, диссипативных квантовых системах, оптике, капиллярных потоках жидкости и мн. др.

Пример 3 : Нелинейное уравнение Шредингера с логарифмической нелинейностью. Рассмотрим уравнение следующего вида ¹¹ :

i 2 V ^+^g  ln м² ,                          (13)

zx ²

где ^=^ x , z , V V x , z и gg z . Решение уравнения (13) находится с помощью т.н. «анзатца – ansatz» в следующем виде: >р = рzeⁱ x , ^z      x , z , тz .

Подставляя данный анзатц в (13) получим: iG ф log |ф|² , где G – постоянная и имеем специфические формы для линейных и нелинейных коэффициентов в виде g G ² , V = —ту ²   2glog р , соответственно, и со следующими уравнениями ограничений:

• ²_z + ² р ² г] xx   0,   Сz +²7 _{x x} 0, xx 0,   г z =   _x ² .     Из условия      С xx   0 следует

ос В

Q = а zx+ р x , Тогда 4 = --^zx ^{2    z} z , где функция Y z введена после

42а интегрирования по координате x . Тогда нетрудно получить из соотношения р222xx 0

выражение р = Ja , а из т ² следует, что т = fa² dz .

Тогда для линейных и нелинейных коэффициентов получим

V= 8z x ² z x     z , g G ² ,

где б = а zz     z ,        zz z z ,                zGа2 log .

14а  2а2,  2   2а   а2z,  3 z  4а 2  G log .

Положим, что *=Ф с, exp iST получим:

ф = exp

8 +G 1 G <² 2 G

Рассмотрим частные случаи решения (14) выбором различных значений параметров а , Р и/

Вариант 1. Пусть ОС — 1, р = - sin со z и/ выбирается из условия 8   0 .Тогда 8   0 и

₂ = СО ² sin СО z / 2. В этом

со случае V z      sin соz x и g G ; имеем также     xsin z и т = z . Амплитуда и

^ ⁼ ^1-2 x-СО cos СО z cos

фаза анзатца задается из условия р = 1 и имеем соz , соответственно.

На рис. 7 показано поведение линейного потенциала (коэффициента) и интенсивность поля 2

при G 1 (самофокусирующаяся нелинейность), 8 = -G и 0) = N 2 .

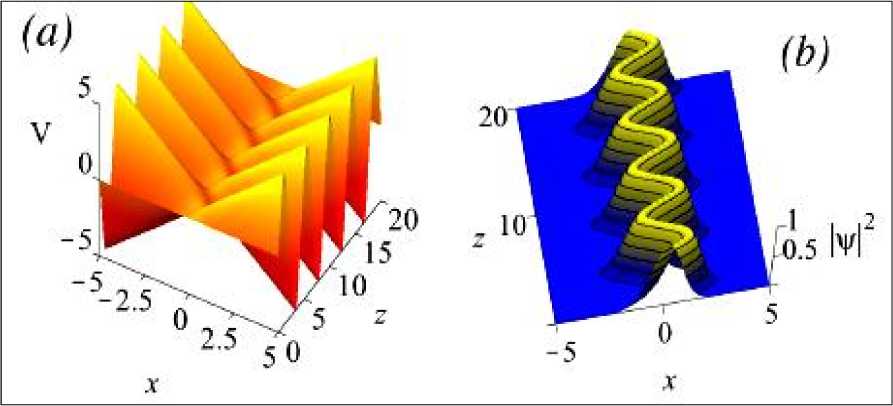
Рис. 7. Вид линейного потенциала (а) и модулированного решения для Варианта 1 (в)

Из рис. 7 видно, что потенциал имеет зигзагообразную форму (рис. 7,а), что порождает осцилляции интенсивности поля (рис. 7,в).

Вариант 2. Предположим теперь, что имеем нелинейные коэффициенты с осциллирующей амплитудой. Например, допустим, что а = 1+ cos² со z  /2, р =0 и/ выбрана так, что 8   0

Тогда ^ = [0.5 +0.5cos² 6У zx  и ^т^ L 11cos со z + 2 cos со z sin со z + 19 (Оz /32 <0 .

1 5cos² z 2cos⁴ zG              2

Имеем также V = -------------------- 7 ----- со ² x ², g = —1+ cos² СО z .

2[1+ cos² со z ] ₂          x , g ₄ 1 cos z .

Амплитуда и фаза решения задается как

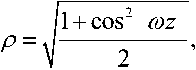
со cos соz sin со z 2 1+ cos2 со z x2 +7 ,

соответственно, где / = - G 1+cos² z ln 1 cos² CD z

Данные параметры позволяют получить новое решение для у/ . На рис. 8 показан профиль для и ² при G 1 (самофокусирующаяся нелинейность), 8 = -G и СО =1.

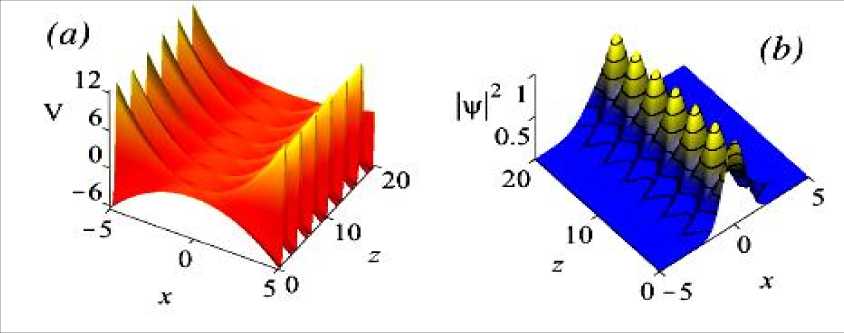
Рис. 8. Вид линейного потенциала (а) и модулированного решения для Варианта 2 (в)

Из рис. 8 видно, что потенциал приобретает форму машущей крыльями птицы, что приводит к формированию осцилляций типа «дышащих вершин».

Вариант 3. Наложим более сложные условия на линейный потенциал в виде комбинации линейного и квадратичного члена от x и периодической модуляции по координате z . Тогда имеем а =

¹1+ cos² CDz ,       2sin z

и/ выбрана так, что б 0 .

Такой выбор приводит определению параметров:

—Г1+ cos² CD z x 2sin z ,      ¹ 11cos CD z + 2cos³ CD z sin CD z + 19 CDz ,

2                     32to       1        111

cc 2 1 5cos2 CDz2cos4

1                                      2

2 1+ cos² CD z ²

1+ cos² CD z ²

2 CD           cos² CD z sin CDz 8 CD cos CD z CD cos CD z sin CD z

2 G 2

Тогда V = <5 x2 x и g =~L1+ cos2

z . Амплитуда и фаза определяются

как

р^

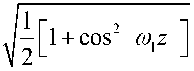
cos св z sin св z

^, П = 11    1

2 1+ cos² со z

x2

2 CD cos СО2Z

1+ cos2

С6 1 ^z

+ / , соответственно, и

G      2

/-  4 L1 cos

СОz ln

1

1 cos2z

21

На рис. 9 показаны линейный потенциал и

4 со2cos2z

1+ cos2 со z

профиль решения       ²

при

G1,        G,CD          1.

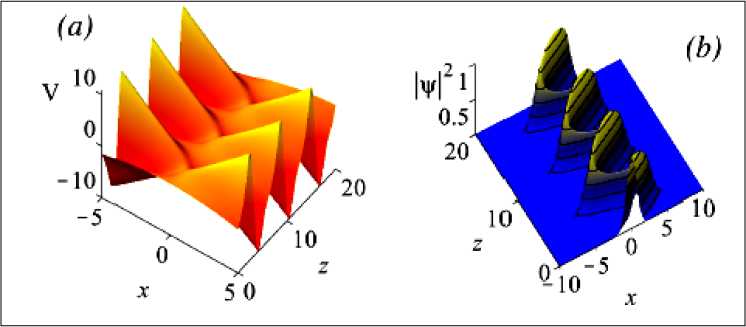
Рис. 9. Вид линейного потенциала (а) и модулированного решения для Варианта 3 (в)

Данный тип модуляции приводит к осцилляциям в x -направлении с осцилляциями типа «дышащих вершин». Решения также имеют квазипериодические осцилляции в x - и / или z -направлениях и зависят от отношения со / как иррациональных чисел.

Рассмотрим кратко важный вопрос устойчивости полученных решений.

Вводятся понятия мощность (норма) и энергия решения в виде:

P = (И2 dx и E = / 1^x2+Vи2+gи 2 log и2 1 dx , соответственно.

Для исследования устойчивости для рассмотренных выше решений осуществляется оценка чувствительности на случайное возмущение амплитуды решения в виде ^ = ^₀ 1+ 0.05 <1 x , где V ₀ = у/ x ,0 – аналитическое решение для Вариантов 1, 2 и 3 и x е -0.5,0.5 является случайной величиной с нулевым средним в каждой точке дискретной решетки интегрирования.

Для рассмотренных Вариантов решений на рис. 10 показаны результаты численного моделирования распространения возмущенного сигнала.

(а)

(б)

(в)

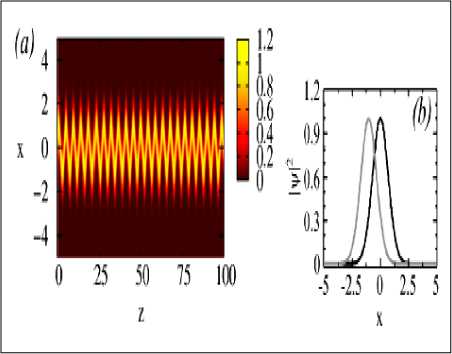
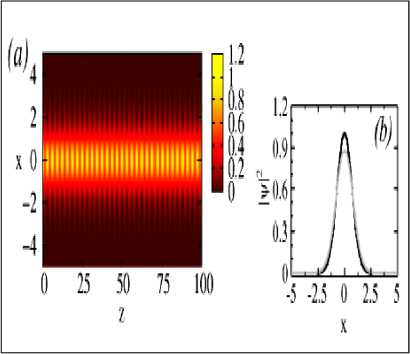
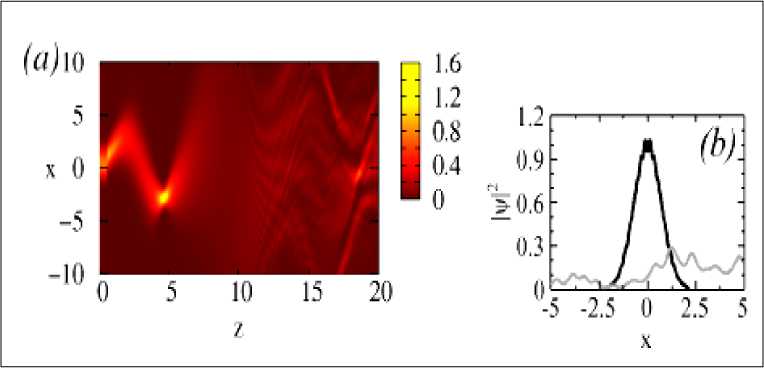
Рис. 10. Графики решений для Варианта 1 (а); для Варианта 2 (б) и для Варианта 3 (в) в плоскости xz и сравнение между входным и выходными сигналами

Входное значение состояния ^ x ,0 для z 0 сравнивается с выходным сигналом при z 1000 . Для Варианта 1 норма равна P ≈1.76911 со стандартным отклонением 5X 10 ¹³ и энергией E ≈90±14; для Варианта 2 имеем P ≈1.76911 со стандартным отклонением □ 10 и энергией E ≈49±12 (с осциллирующей частью).

Из рис. 10,а,б следует, что оба решения Вариантов 1 и 2 устойчивы.

В случае Варианта 3 решение неустойчиво при норме P ≈1.77096 со стандартным отклонением □ 10 и энергией E ≈186±184 (со случайными траекториями в области неустойчивости) в конечном состоянии z 20 .

В этом случае Варианта 3 модуляция приводит к неустойчивому состоянию.

Рассмотрим частный случай (5) для моделирования динамического поведения вращения кубита в парах не расположенных рядом квантовых точках.

Пример 4: Моделирование вращений кубита в квантовых точках. Уравнение Шредингера, описывающее динамику эволюции электронных систем, имеет следующий вид:

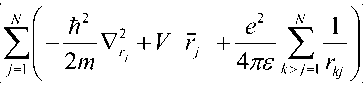
решить с использованием полиномов Чебышева в виде:

i 71 — W r , t б _t r ,

r,t . Данное уравнение можно эффективно r,t exp i Emax  Emin t    JnTniH r,0 , где Emax  и Emin  – верхняя и нижняя границы энергии в точках численной решетки, Jn    - функция Бесселя первого порядка, T

– полиномы Чебышева. Нормированный Гамильтониан системы определяется как H 2H  Emax  Emin /Emax  Emin  с гарантированной сходимостью. Все электроны системы расположены на одинаковых энергетических уровнях и эволюционируют когерентно во времени при взаимодействии друг с другом. В принятых предположениях на рис. 11,а показана эволюция электрона в системе взаимосвязанных квантовых точек в соответствии с приведенным выше уравнением движения электронов.

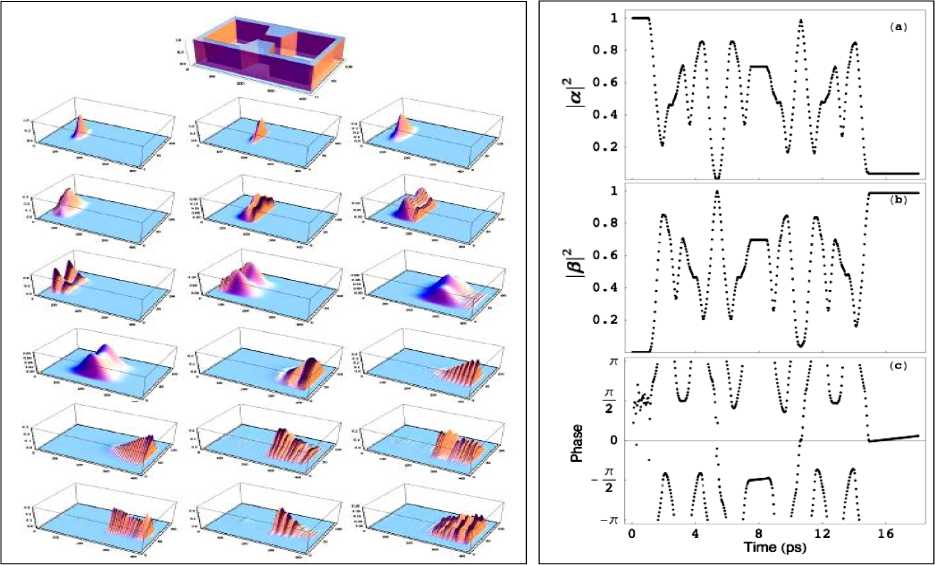
(а)                                                     (б)

Рис. 11. Эволюция волновой функции в системе связанных квантовых точек (а) и вращение кубита на сфере Блоха в разные моменты времени (б)

Все возможные вращения кубита на сфере Блоха могут управляться центральным потенциальным барьером и / или электрон – электрон взаимодействиями как показано на рис. 11,б, которые эквивалентны квантовым случайным блужданием на решетке ¹² .

В этом случае амплитуды и фазы для перехода влево L или вправо R показаны на рис. 11,б для различных моментов времени.

Пример 5 : Информационно-термодинамические модели решения уравнения Шредингера . В общем случае класс уравнений типа (8) имеет вид:

i           r, t

t

U r,t F r,t 2m

r,t

с Лагранжианом:

12Manouchehri K., Wang J.B. Solid state implementation of quantum random walks on general graphs // arXiv:0811.1795v1 [quant-ph] 11 Nov 2008.

i

L r, t

2t

dtp d^ip

t

t

й2

- — V^ Vy/- U ^V + G и ²     ,

р где G        1 Fрdр . Для стационарного состояния r, t = ЦТ r exp i соt и энергия

Eу

имеет вид

E Ху = /?(У + C+ /G м 2 _F 2

. Для логарифмических нелинейностей

F р =-b ln рaⁿ и G р =-b ln рaⁿ + b при C b имеем E гр =ha)

В общем виде E хр = й² /2 m (Vy'lv^ + ^l U l^)^- b (^1ln и 2 _an 1^) и

E у/ 1V2Eу/ 1 +E^2 . Если p=V r, t I интерпретировать как плотность распределения kk вероятностей и у/ r        p у/r r, ^ p 1 , то из выражения для E V получим следую- i1i1

k щее выражение для изменения энергии:  E b^ pilnpi.

i 1

Таким образом, нелинейная часть изменения функционала энергии имеет форму информационной энтропии Шеннона b 0 . Установленная взаимосвязь между решениями уравнений типа Шредингера и энтропией привела к широкому использованию информационнотермодинамических подходов к исследованию квантовых систем.

В частности, широкому обсуждению подверглись соотношения неопределенности Гейзенберга с точки зрения энтропийных оценок наблюдаемых (измеряемых) величин в квантовой нерелятивистской механике. Так, например, для известных соотношений неопределённости наблюдений пары L_z — ф «момент – угол» (из общего энтропийного соотношения для двух наблюдаемых А и В в виде S ^A S ^B b ) имеем соотношение: SS^Lz ln Кф /2 л . Аналогично для пары «положение - импульс» типа xp имеем:

S^xS^p 1 ln2 ln У , у = - .

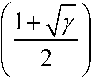
Другой оценкой в данной ситуации является S^xS^p 2ln

Отметим, что значение энтропии S определяется через волновую функцию 1^ t , x | как

S       t , x | ln 1^ t , x | . Тогда для пары «угол-момент» имеем соотношение в виде:

dx kl 2 ln к|2- J dpй|у/|2 ln и21+ ln 7Г , где Фp2тгй Ѕ dxe ipx / h.

Таким образом, можно получить нижние границы точности наблюдений в терминах энтропии наблюдений, не решая волновых квантовых уравнений.

Пример 6. Для линейного гармонического осциллятора в стационарном состоянии уравнение Шредингера имеет вид HEф , H – гамильтониан, E – его собственные значения (уровни энергии, см. выше примеры). Пусть ф — ^АAii, где ф – собственные функции оператора H , i1

соответствующие собственным значениям E . Если в момент времени t состояние квантовой системы описывается волновой функцией фХ = ^ДХф., и в момент времени t2 состояние i1

квантовой системы описывается волновой функцией ^2 = ^ Д² ф. то количество информации i 1

относительно энергетических уровней задается в следующем виде:

I          =±|А. ² flog A .

i 1                A_i 1

где вероятность P Ei  нахождения системы на энергетическом уровне E определяется как

P E =|A | . Для гармонического осциллятора имеем E_n=h(o\nA-^\ и собственные функции

а

n

e

x ²

2H x,

. m - масса осциллятора, к - коэффициент жесткости.

Пусть E 0 и E ₀2

E01 = 1И и

- два основных состояния осциллятора с основными частотами <в_х и 6У₂. Тогда

2

E0

1 +

= -тко, . 2²

0121e12x2

NTT

= e^ e “xx  и

искомое количество

информации равно :

1

i 1

2logAAii1222

xlog2

01

x

x

•

₂    log ₂

Из зависимости количества информации I ²¹

E0 / E0  получим, что для извлечения энергетических уровней E02 / E0  = 9,8

£

2

log2 e

от отношения

одного бита информации

2 Л

12

22

-1

энергетических уровней

требуется соотношение

или E ₀²/ E ₀¹0,28 . При этом локальная точность

xxx

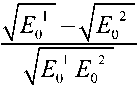
, где x

4 mE

•

Пример 7 : Свойство решения Шредингера для свободной частицы и энтропийные оценки неопределенности . Рассмотрим уравнение Шредингера для свободной частицы ( m = 1, h = 1)

2

следующего вида: г ---= —— , которому соответствует семи фактор-алгебра Ли с базисом из tx ²

операторов. Решение данного уравнения, как известно, имеет вид:

q, t Ai

B

2/3

B3t2

q  4m2

exp

iB3

2m

B3t2

6m2

.

где Ai - функция Эйри, и не расплывается как волновой пакет, а равноускоренно движется в виде не

B3t2

расплывающегося пакета со скоростью      . В квантовой механике динамика свободной частицы

2m2

задается в гильбертовом пространстве  L²R³   унитарным оператором U t e ^{itH 0} где

H       p ², t e ^{itH 0}  . При       1 и t 0 имеем следующее энтропийное неравенство

2m

S 2 S      t 2    3 ln t 1  .

m

С течением времени t 0 в общем случае имеем S    t     S     , т.е. имеем энтропийную оценку расплывания волнового пакета по отношению к исходному состоянию.

При движении частицы в постоянном электрическом поле H H E r , E E e имеем U t e ^itH и S ² S     t ² 3ln ^Et .

m

Таким образом, при tt получим 3ln t ² S    t ² S ² и имеем энтропийную

m оценку возрастания неопределенности наблюдения локализованной в пространстве частицы.

Для оператора Q состояния частицы Q, Q, дисперсияQ2     , Q Q 2    для свободной частицы teitH имеем: 2

t Q 2     Q 2  2 1 QP PQ Q P tP 2 t2 ,

2     mm

где P2    P P 2    P 2 dP.

Vr    2

При наличии потенциала V sup       dr     существует постоянная C R такая, что r R3  rr exp it H V         Ct 3/2     , t 0,    L2 R3   L1

S ² S exp it H V

R³ и имеем энтропийную оценку ² 3ln C ^2/3 t .

Уравнение Дирака для заряженных частиц со спином s = S , находящихся в заданном электромагнитном поле

Согласно квантовому постулату для частиц со спином s Ѕ число компонент волновой функции должно равняться 4 s 2 4 . Как известно, объект, описываемый этими волновыми функциями в уравнениях Дирака, является спинором [6-11]. Компоненты спинора имеют своеобразные законы преобразования, представленные в [12, 13, Табл. 4.2, с. 225]. Так как уравнение Дирака является уравнением первого порядка      1 , то согласно квантовому постулату имеем

2s 1   2 . Таким образом, в соответствии с алгоритмом квантового постулата для частицы со спином s  Ѕ трансформированное уравнение Гамильтона-Якоби следует возвести в степень 2.

В результате имеем m2c2

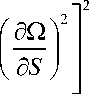
2

e

Aj xj c     S

Уравнения классического аналога уравнений Дирака, согласно [12, 13], будут иметь вид

0	p 0 mcp	p 1 ip 2	p 3	Y 1
p 0 mcp	0	p 3	p 1 + ip 2	ф 2	0,  (16)
p 1 ip 2	p 3	0	p 0 + mcp	ф 3
p 3	p 1 + ip 2	p 0 + mcp	0	кФ 0 J

„ a e                                     1a ie 0

где pj          AjpS; pS      , j 1,2,3; p0 = -T- —

cx cj   оScоtc

В (16) использованы «векторные» потенциалы A ₁ , A ₂ , A ₃ и «скалярный» потенциал ф ⁰ вместо 4-потенциала A . Для того, чтобы получить в качестве характеристического многообразия уравнений (16) трансформированное уравнение (15) , необходимо после всех выкладок произвести замену t x / ic ix / c .

x , x , x , t exp

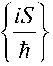
h 8

ic 8t

С помощью указанной подстановки вида ф x ,x ,x ,t,S = у/ получим

0 p  mc p1 ip2 p3    Y ф1 p  mc p1 ip2 0 p3 p3 0 p1 + ip2       2 0, p+ mc   ф3 (17) p3 p1 + ip2 p+ mc 0 JU0J или в традиционной форме P mc 1       P1 iP2 V 0 P Vх    0 P mc 2      P1 iP ^3 + P3 V00 (18) P mc Vх 3      P1 iP2 V2 P3 ф1     0, P mc Vх 0      P1 iP ч* ! + P3 V20 где Pj        i, j 1,2,3; P0

ix ⁱ

Система уравнений Дирака (18) является релятивистски-инвариантной со следующими законами преобразования компонент ф , представленных в Табл. 2.

Нетрудно заметить, что компонент   у/k k 0,1,2,3 существенно отличаются от соответствующих формул преобразований для компонент векторных и тензорных объектов.

Таким образом, из требований релятивистской инвариантности и о едином математическом объекте с равноправными компонентами (фундаментальными функциями 14/ ) следует, что имеем дело с новым (по сравнению с векторами и тензорами) математическим объектом, который носит название спинора , а соответствующее поле (18) называется спинорным.

o Общее решение уравнений Дирака для свободных полей . В теории линейных уравнений в частных производных известен следующий метод. Пусть дана однородная система линейных дифференциальных уравнений (обыкновенных или с частными производными) с постоянными коэффициентами следующего вида:

n

х eijuj   0 i 1,2,   ,n ,                             (19)

j 1

где u – искомые функции любого числа независимых переменных x ,, x ; e – операторы дифференцирования по этим переменным любого порядка и структуры. Требуется выразить u через

^ ,,, ф , каждая из которых определяется независимо от другой из своего дифференциального уравнения (связь между функциями ф сохраняется в граничных условиях).

Таблица 2. Преобразования компонент спинора у/ в уравнении Дирака

Вид преобразования	Преобразование операторов p	Преобразование операторов у/ к
Вращение вокруг оси OZ	p p cos а — p sin а p p cos а + p sin а p 3 p 3 ; p 0 p 0	1230 ^^         x 1 , x 2 , x 3 , x 0 exp     i 1230 ^^         x 1 , x 2 , x 3 , x 0   exp i 1230 x 1 , x 2 , x 3 , x 0 exp     i 1230 V 00 x 1 , x 2 , x 3 , x 0 exp i
Вращение вокруг оси OY	p p cos 0 + p sin У p p cos 0 — p sin 0 p 2 p 2 ; p 0 p 0	,             0 .       . 0 ч* 1 — у/ cos        sin ,            0       . 0 2 — у/ cos       sin ,              е .       . 0 ^31 cos+ у/ 0 sin2 ,            0        . 0 0 —  0 cos       3 sin
Простое преобразование Лоренца	p 3 p 3 ch у + p 0 sh Г p 0 p 0 ch у + p sh Y p 1 p 1 ; p 2 p 2	ч* 1 = w 1 ch       3 sh 2    — 1// 2 ch        0 sh 3    — у/3 ch       1 sh 0 — ^/0 ch       2 sh

Полагая в уравнении Дирака (18) для i 2,3,  , n

uj1kj101 j 1,2,   ,n ,                              (20)

неизвестные операторы дифференцирования k ¹ определяются как решения линейной системы

n 1 алгебраических уравнений	n eijkj 1    0      i   2,3,   , n .                                (21) j 1
Из этой системы определяем	kj 1     E 1 jC 1 ,                                             (22)
где   E ij    i , j 1,2,   , n   обозначает оператора	алгебраическое дополнение элемента e  определителя-

В (22) через C обозначен оператор, который можно считать единичным, что сводится к замене

C 11 на ф 1 , т.е.	uj 1     E 1 j 1 .                                                  (24)
Складывая все u s	s 1,2,  , n , получаем e 11     e 12            e 1 j 1      ф 1           e 1 n n u j       E sjф s                                                              (25) s 1 n 1 n 2             nj 1       n            nn

E

e ₁₁    e ₁₂

e1n

.

ee n1n2

e

nn

причем все ф _s  s 1,2,  , n удовлетворяют одному и тому же дифференциальному уравнению

Eфs   0.(26)

Применяя этот метод к уравнениям Дирака (18) при A 0 , нетрудно получить, что функции

V_i i 0,1,2,3 должны представлять собой некоторые линейные комбинации производных четырех линейно независимых решений следующего линейного волнового уравнения четвертого порядка

(22 л m2m2

•   2•    2-ф =0,(27)

где • – оператор Даламбера. Другими словами, функции ф должны удовлетворять уравнению, в левой части которого оператор уравнения Фока-Клейна-Гордона применяется дважды. Отсюда также следует, что из четырех линейно независимых решений уравнения Фока-Клейна-Гордона можно образовать четыре линейно независимые комбинации их производных, которые будут решениями уравнений Дирака.

Действительно, согласно соотношениям (18), (23) и (26) нетрудно получить следующие соотношения для компонент фундаментальных функций ф через решения ф уравнений Фока-Клейна-Гордона:

у 1  ) p 0 mc ф2+ p1 + ip2 ф3  p 3ф0, ф 2  )     p 0+ mc ф1  p 3ф 3    p1  ip2 ф0,

(28) ф 3  )     p 0+ mc ф 0   p1 + ip2 ф1+ p3 ф2, ф 0  )   p0  mc ф3+ p3 ф1+ p1 + ip2

где ^ , ф , ф , ф – линейно независимые решения уравнения (26). В нашем случае, уравнение (26) принимает вид:

)) фj 0,(29)

где оператор уравнений Фока-Клейна-Гордона вида:

• )    p12 + p22 + p32 + p02 + m2c2; pj = h—j    j 1,2,3 ; p0

Оxj                       ic оt

Выражения (29), (30) дают своеобразное представление компонент ф спинора через производные четырех линейно независимых скаляров ф , каждый из которых удовлетворяет уравнению Фока-Клейна-Гордона (29).

Рассмотрим другие формы уравнения Дирака.

Другие формы уравнения Дирака . По аналогии с уравнениями Дирака (18) можно написать другие релятивистские инвариантные квантовые уравнения спинорного поля, форма которых приведена в табл. 3.

Преобразования компонент спинора у/ , оставляющих релятивистки инвариантными перечисленные квантовые уравнения, приведены в той же табл. 3. Эти формы, как и форма уравнений Дирака, удовлетворяют законам сохранения плотности вероятности, энергии и градиентной инвариантности. Подробно для уравнения Дирака перечисленные свойства исследованы Луи де Бройлем. Общее решение любой из перечисленных форм для свободных полей также может быть представлено в виде, аналогичном (18).

Таблица 3. Преобразования компонент квантовых волновых уравнений

№	Квантовые уравнения	Преобразование компонент Ф
		Поворот вокруг оси OZ	Поворот вокруг оси OY	Простое преобразование Лоренца
1	p+ mc у/ 1+ p+ ip у/3+ p у/ 0 p 0 + mc 2 p 1 ip 2 0+ p 3 3 0 p 0 mc у/ 3+ p 1 ip 2 1+ p 3 2 0 p 0 mc 0 p 1 + ip 2 2+ p 3 10	у/1    1exp    iа /2 W     exp iа /2 у/     exp iа /2 у/0    0exp   iа /2	у/ 1 — у/ cos 9 /2 -у/ sin 9 /2 у/ — у/ cos 9 /2 ^^ sin 9 /2 у/ з — у/ cos 9 /2 -у/ 0sin 9 /2 у/ о — у/ cos 9 /2 ^W sin 9 /2	V    ; =v ch У /2 +Ч/ sh У /2 V    ; =^ ch У /2 "V sh У /2 V    ; =^ ch У /2 +у sh У /2 V    ; =v ch У /2 -^ sh У /2
2	p mc у/ p+ ip у/ p у/ 0 p 0 + mc 2 p 1 ip 2 ^1 p 3 0 0 p 0 + mc ^3+ p 1 ip 2 0 p 3^10 p 0 mc у 0+ p 1 ip 2 ^3 p 3 2 0	у/1    1exp    iа /2 у/      exp iа /2 у/3    3exp   iа /2 у/0    0exp iа /2	у/ 1 — \р cos 9 /2 -у/0sin 9 /2 у/ — у/ cos 9 /2 -у/ sin 9 /2 у/ з — у/ cos 9 /2 ^W sin 9 /2 у/ о — ^/ cos 9 /2 ^^ sin 9 /2	V    ; =^ ch У /2 +ч/ sh У /2 V ; =y ch У /2 "V sh У /2 V    ; = ^ ch У /2 -у/ sh У /2 V    ; =v ch У /2 +V sh У /2
3	p 0 mc   1     p 1   ip 2   3    p 3  2 0 p 0 + mc   2    p 1 + ip 2 у 0   p 3 1 0 p 0 mc   3    p 1   ip 2 V 1+ p 3 0 0 p 0 + mc у 0    p 1   ip 2 у 2+ p 3 30	у/1    1exp    iа /2 у/ 2    2exp   iа /2 у/     exp iа /2 у/0    0exp iа /2	Ч^ 1 — ^/ cos 9 /2 ^W 0sin 9 /2 — ^/ cos 9 /2 +^ sin 9 /2 W з — ^/ cos 9 /2 -^ sin 9 /2 Y о — ^/ cos 9 /2 "У sin 9 /2	; = 4* ch У /2 "V sh У /2 V ; =^ ch У /2 +V7 sh У /2 V ; =^ ch У /2 "V sh У /2 V ; =v ch У /2 +у sh У /2
4	p 0 mc 1 p 1 + ip 2 0+ p 3 2 0 p+ mc у/2+ p+ ip у/3+ p у/ 0 p 0 mc ^3+ p 1 ip 2 У 2+ p 3 ^0 0 p 0 + mc ^ 0 p 1 ip 2 ^1+ p 3 30	у/1    1exp    iа /2 W 2    2exp   iа /2 у/ 3    3exp   iа /2 у/0    0exp iа /2	1 — ^/ cos 9 /2 ^^ sin 9 /2 Y — ^/ cos 9 /2 -W 0sin 9 /2 W з — ip cos 9 /2 ■^ sin 9 /2 Y о — ^/ cos 9 /2 ^W sin 9 /2	; = 4* ch У /2 "V sh У /2 V ; =^ ch У /2 +V7 sh У /2 V ; =^ ch У /2 "V sh У /2 V ; =v ch У /2 +у sh У /2
5	p 0 mc 1+ p 1 + ip 2 2 p 3 0 0 p+ mc у/2+ p ip у/ 1 + p у/ 0 p 0 mc ^3+ p 1 ip 2 ^0+ p 3 ^2 0 p 0 + mc У 0+ p 1 + ip 2 ^3 p 3^10	у/1    1exp    iа /2 у/      exp iа /2 у/     exp iа /2 у/0    0exp   iа /2	1 — у/ cos 9 /2 ~W sin 9 /2 Y — ^/ cos 9 /2 -W 0sin 9 /2 W з— ^ cos 9 /2 + ^ sin 9 /2 — ^/ cos 9 /2 + ^ sin 9 /2	V    ; =v ch У /2 +^ sh У /2 V    ; =^ ch У /2 "V sh У /2 V    ; = ^ ch У /2 +V sh У /2 V    ; =v ch У /2 -^ sh У /2

В табл. 4 и 5 приведены зависимости у/ от ф для систем в табл. 3.

Следует подчеркнуть, что формы, представленные в табл. 3, отражают требование о равноправности компонент фундаментальных функций ф .

Таблица 4. Общий вид решений систем квантовых уравнений из табл. 3

Компоненты	Общий вид решений системы квантовых уравнений для свободных частиц со спином s Ѕ
	Система 1 в табл . 1.2	Система 1 в табл . 1.2
1	)       p 0   mc 2    p 3 3     p 1   ip 2   0	)       p 0    mc 0    p 3 2     p 1 ip 2   3
2	)     p 0   mc 1     p 1 ip 2   3    p 3 0	)     p 0   mc 3     p 1   ip 2   0 p 3 1
3	)     p 0 mc 0     p 1   ip 2   2    p 3 1	)       p 0 mc 2     p 1    ip 2   1    p 3 0
0	)       p 0 mc 3     p 1    ip 2   1    p 3 2	)     p 0 mc 1     p 1 ip 2   2    p 3 3

Таблица 5. Общий вид решений систем квантовых уравнений из табл. 3

Компоненты	Общий вид решений системы квантовых уравнений для свободных частиц со спином s Ѕ
	Система 3 в табл . 1.2	Система 4 в табл . 1.2
1	)       p 0   mc 2    p 3 3     p 1   ip 2   0	)     p 0    mc 3 p 3 0     p 1   ip 2   2
2	)     p 0   mc 3    p 3 0     p 1    ip 2   1	)     p 0   mc 0    p 3 3     p 1    ip 2   1
3	)       p 0 mc 2    p 3 1     p 1 ip 2   0	)       p 0    mc 1    p 3 2     p 1 ip 2   0
0	)     p 0    mc 1    p 3 2     p 1   ip 2   3	)       p 0   mc 2    p 3 1     p 1 ip 2   3

Аналогичный вид имеет решение системы 5 из табл. 3.

В заключении отметим следующее. В уравнениях Дирака выделена преимущественная ось oz , т.е. квантовая система движется относительно оси oz . Так Луи де Бройль [14, с. 11] отмечает: «Уравнения Дирака приписывают особенную роль оси oz и волновые функции, также как и в теории Паули, дадут ответ на вопросы, в которых играет роль ось oz ». Математически это нашло свое отражение в распределении комбинаций операторов вида p ₀ mc , p ₁ p ₂ , p ₃ .

Изложенный выше подход, основанный на требовании о единстве математического объекта, равноправности его компонент и координат пространственно-временного континуума, позволяет непосредственно написать системы квантовых уравнений относительно других направлений пространственно-временного континуума, аналогичные представленным в данном разделе.

– Системы квантовых уравнений Дирака относительно других направлений в пространственно-временном континууме. Так, например, уравнения Дирака для случая, когда система движется в направлении оси oy , принимают вид :

p 0   mc   1    p 1 ip 3   0 p 2 3   0 p  mc      p  ip      p     0 0           2      1      3    3     2  0                                     (31) p 0   mc   3     p 1   ip 3   2    p 2  1   0 p 0   mc   0     p 1   ip 3   1    p 2  2   0

Аналогично для случая, когда система движется в направлении оси ox , имеем

p 0   mc   1     p 2   ip 3   0    p 1  3    0 p  mc      p  ip      p    0 0            2       2      3    3      1  0       .                                (32) p 0   mc   3     p 2   ip 3   2    p 1  1   0 p 0   mc   0     p 2   ip 3   1    p 1  2   0

Для полученных систем нетрудно выписать преобразования компонент у/ и общие решения для свободных частиц через оператор Фока-Клейна-Гордона подобно результатам, представленных в табл. 3 и 4. Так, для системы (31) имеем

V ₁   )    p ₀ + mc ф 2+ p ₁   ip ₃ ф ₃   p ₂ ф 0

ф ₂   )      p ₀+ mc ф ₁    p ₁ + ip ₃ ф ₀ p ₂ 3

.                        (33)

ф ₃   )      p ₀ mc ф ₀    p ₁ ip ₃ ф 1+ p ₂ ф 2

ф ₀   )    p ₀ mc ф 3+ p ₁ + ip ₃ ф 2+ p ₂ ф 1

Соответственно для системы (32)

ф 1   )    p ₀ + mc ф 2+ p ₂   ip ₃ ф ₃   p ₁ ф 0

ф ₂   )      p ₀+ mc ф ₁    p ₂ + ip ₃ ф ₀   p ₁ 3

.                       (34)

ф ₃   )      p ₀ mc ф ₀    p ₂ ip ₃ ф 1+ p ₁ ф 2

ф ₀   )    p ₀   mc ф 3+ p ₂ + ip ₃ ф 2+ p ₁ ф 1

Аналогично табл. 3 можно выписать соответствующие законы преобразования компонент для систем (31) и (32).

Таким образом, приведенные математические объекты полностью обладают свойствами, присущими модели Дирака.

– О ковариантности уравнений Дирака и симметричные типы уравнений для частиц со спином s Ѕ . Общее требование релятивистской ковариантности уравнений Дирака сам автор провел следующим образом. Рассматривалась исходная система координат oxyz , которую будем обозначать через S , и система координат o x y z (система S ), которая движется равномерно и прямолинейно вдоль оси oz относительно системы координат S .

Дирак совершает переход от системы координат S к системе координат S следующим образом. Вначале совершается поворот системы S вокруг оси oz на определенный угол ОС (см. табл. 3). Эту промежуточную систему координат будем называть S . Показывается, что при переходе от S к S уравнения остаются ковариантными, причем функции k k 1,2,3,0 преобразуются при этом по особому закону, не имеющему ничего общего с преобразованиями векторных величин. Далее совершается поворот системы S на угол р вокруг оси ox . Полученную таким образом вторую промежуточную систему будем обозначать также через  Sар  Далее показывается, что уравнения остаются ковариантными при переходе к системе координат Sар . При этом четыре функции ^ подвергаются новому преобразованию, также ничего не имеющего общего с преобразованиями векторных или тензорных величин (см. табл. 4).

И, наконец, совершается преобразование к системе координат S , движущейся равномерно и прямолинейно по отношению к системе координат S , S и Sар .

Дирак показывает, что если функции ^ преобразуются по определенному указанному выше закону, то в системе координат S уравнения будут сохранять тот же вид, который они имели в системах координат S , S и S_ар .

Другими словами, уравнения Дирака являются общековариантными. Дирак, а позже фон Нейман показали также, что каждое из введенных преобразований может рассматриваться как элемент некоторой группы. Таким образом, был открыт новый в смысле Вундгейлера математический объект, изучение которого привело Ван дер Вардена к созданию спинорного исчисления. Впрочем, вне связи с квантовой механикой Э. Картан еще в 1913 г. разработал основы спинорного исчисления.

Обратим теперь внимание на следующее существенное обстоятельство. Переход от системы координат S к системе координат S производится в следующей последовательности: S S S S . Изменение указанной последовательности недопустимо ввиду некоммутативности введенных преобразований. Если бы, например, совершить сначала переход к системе координат, движущейся равномерно и прямолинейно вдоль оси oz системы S (причем оси этой системы координат остаются все время параллельными осям системы S ), а затем совершить два указанных выше поворота, то пришли бы к системе координат, не имеющей ничего общего с системой координат S .

Таким образом, матрицы операторов преобразований к системам координат S , S и S оказываются некоммутативными.

Вместе с тем операторы импульсов p , p , p , p входят в уравнение Дирака неравноправно. Так, операторы p и p входят в виде комплекса p ₁ ip ₂ , в то время как оператор p входит самостоятельно, а оператор p также входит в виде комплекса p ₀ + mc . Эта неравноправность операторов как будто бы противоречить равноправности всех направлений в пространстве и противоречит вытекающей из теории относительности симметрии между пространственными координатами и координатой времени.

Тем не менее, остается фактом, что уравнения Дирака остаются инвариантными относительно групп преобразований S , S SаР и SSар S . Причем направление оси oz в системе координат S может иметь любой угол по сравнению с начальной системой координат S . Поэтому Луи де Бройли совершенно прав, когда сделал в [14, c. 111] утверждение: «Комбинируя три типа преобразований 1, 2 и 3 можно получить преобразование Лоренца наиболее общего типа». Вместе с тем в [14, c. 229] Луи де Бройли отмечает: «Тем не менее совершенно невозможно претендовать на то, чтобы теория Дирака в ее нынешнем состоянии целиком с концепциями относительности. Одной из ведущих идей теории относительности является то, что она всегда заставляет пространственные и временные координаты входить в уравнение симметрично. Но в теории Дирака эта симметрия переменных x , y , z , t не осуществляется».

Невольно возникает вопрос: не существует ли аналогичная уравнениям Дирака система уравнений, в которую операторы p входили бы равноправно, была бы релятивистки инвариантной и удовлетворяла квантовому постулату?

Если бы эта система уравнений приводила к тем же результатам для спектра атома водорода (тонкая структура), что и уравнение Дирака, а также к другим физически эффектам (существование позитрона и др.), то такая система уравнений могла бы быть конкурентоспособной по отношению к уравнениям Дирака. Уравнения эти имеют следующий вид:

p ₀ ip ₃ V ₁     p ₁   ip ₂   0 mcV 3 0

p ₀ ip ₃ V 2    ^p 1 + ip ₂ W 3+ mc W 0 0

p+ ip  у/    p  ip  у/ mc^   0

p ₀   ip ₃ ^0    ^p 1 + ip ₂ V 1+ mc ^2 0

p ₀ ip _{2 1} p ₁ ip ₃ 0 mc V 3 0 p ₀ ip ₂ V ₂ p ₁ + ip ₃ 3+ mc 0 0 p+ ip У⁷ p ip У⁷ mcV 0

p ₀ + ip ₂ V ₀ p ₁ + ip ₃ ^1+ mc ^2 0

. 5     ie

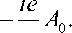
c

где pjj      Aj; p0

x    c           ic Оt

Нетрудно показать, что такие системы релятивистки инвариантны и что они приводят к тем же собственным значениям, что и уравнения Дирака при рассмотрении задачи о спектре атома водорода. Особенности решений уравнений Дирака типа Zitterbewegung и связь с задачами квантового поиска рассмотрены в Части 5 данной работы.

Здесь кратко остановимся модели квантового блуждания в форме уравнения Дирака.

Пример 8 : Дискретные квантовые случайные блуждания и уравнение Фока-Клейна-Гордона (ФКГ). Рассмотрим выражение:

wj , t+ 1    cos О у/   j+1,t   isin О у/   j 1,t ,

W   j , t+ 1    cos 6 щ   j 1,t   isin 6 у/   j+1,t .

Разрешая последнее уравнение относительно ^ получим:

Lj+ 1,t                R j,t +1 cos 6 у/ R

sin У L

j 1,t ],

^L j , t+ 1               R j 1,t +2 cos О у/ R

sin 0 L

j 2,t +1].

Подставляя данные соотношения для ^R j1,tи^R j,t 1 в получим:

вышеприведенные выражения,

R  j , t+1 +^R  j , t  1   cos 6 ^ Rj+ 1,t +^R  j  1,t ] ,

L  j , t+1 +^L  j , t  1   cos 9 [^Lj+ 1,t + ^L  j  1,t ] .

Вычитая  2^Rj,t 2cos     Rj,t

из обеих сторон первого из приведенных выше

уравнений, уравнение в конечных разностях, и которому соответствует дифференциальное уравнение

следующего вида:

а 9 22

cos           - W  j , t 2 1 cos        j, t при единичном шаге во времени j2t2RR

и пространстве. Аналогичное уравнение может быть выписано для компоненты ^ _L

Примечание . Оператор V , которому соответствует дифференциальный

б оператор     , в бt

hh ^ j,t               j,t конечных разностях имеет вид V =22 th

.

При

h 1 оператор

V, = ^ j , t + 0.5 ^-^ j , t 0.5 , что соответствует дифференциальному оператору . ^t                                                                                                                                                                        t

Поэтому оператор     может рассматриваться как двойное применение оператора в конечных

t2

разностях к двум членам, что означает

V t ^{2    1}

h

^ j , t + 1 -V j , t - V j , t -V j , t  1        j , t +12^ j , t W j , t 1

h

h ²

;

при h 1 имеем в пределе оператор б ² / t ² . Операторы в конечных разностях V иV 2 _j соответствуют дифференциальным операторам б / сj и б ²/ j ² определяется также по аналогии для j при постоянном t . Следовательно, из уравнений для каждой компоненты дискретного квантового случайного блуждания ^ _R j , t и ^ _L j , t следует уравнение ФКГ:

v2122

к для свободной релятивистской частицы со спином s 0 .

Примечание . Эквиваленты скорости света c и массы m для каждой компоненты ^ _R j , t и

VL j, t в динамике дискретного квантового случайного блуждания определяются в виде c cos о,ц = mc 2 sec 6 -1i . При й=1

2 sec в -1 можно записать m cos 9

Отметим, что максимум скорости получается при c 1 , что соответствует о = 0 и m 0 , и находится в соответствии с релятивистскими требованиями, что масса частиц света равна нулю. Данный факт не противоречит также утверждению, что динамика квантового блуждания соответствует при 9 = 0 состояниям |0) , которые расходятся друг от друга без интерференции с максимальной вариацией.

Пример 9 : Дискретные квантовые случайные блуждания в форме уравнения Дирака . В примере 8 было показано, что система связанных уравнений дискретных квантовых случайных блужданий приводит к уравнению ФКГ в форме релятивистской механики. Аналогичное явление имеет место для структур (1 + 1) – размерности релятивистского уравнения Дирака (18) в виде:

iй—- H€ 1^=1 iй—+iкc€ mc2 |у/ =0, (38) д tD) Idt с x mc , где m масса покоя частицы, c – скорость света, iк — – оператор момента, x и t – координаты аt пространства – времени. Матрицы € и € являются эрмитовыми и удовлетворяют условию:

_€ 2 € 2 I,   €^€    €€ _.

Рассмотрим для этого нелинейно связанные уравнения в матричной форме:

_L j , t +¹) vV_R  j , t +¹)

1 cos

0Y wL^j + 1, t

¹Jw _R j 1, t JJ

Так как оператор действия подбрасывания квантовой монеты

sin

B

0, 6 ,

к- ⁱ

и

i

^L^j +1, t

⁰ JWк j-Vt

.

оператор условного сдвига

(39), то выражение (39)

^_L  j , t +1

<^R ,+1

_L j , t Вычитая ^L         cos

W j , t

R

Lj , t   1        Lj , t к^Rj , t   1       Rj , t

B

0, 6,2J

I+ sin

cos

УL^j + 1, t

U _R  j 1, t

L

R

0 I+ sin

cos 6 I+ sin 6 аъ^ат

L^j +1, t

_R j 1, t

.

j,t из левой и правой частей в (40) получим: j,t

9 СТ, <7.

>_Lj 1, t      _Lj , t ]

W _Rj 1, t _Rj , t)

^L  j, t

^R  j, t

cos 0 I+ sin 0 о 3^2

L  j, t

R  j, t

.

Разностная форма (41) может быть представлена в дифференциальной форме как:

в (v _Lj , t t _R j , t

Lj ,t cos О G sin О G— + cos ОIsin           IL jRj ,t

Умножая левую и правую часть (42) на получим [15]:

i й

и преобразуя простыми алгебраическими выкладками,

s I ^Lj ,t i           L

Вt_R j , t

i й

cos О G sin

в

"  — + cos о Isin

2    _j 32

I

_L j , t

_R j , t

.

При 9 = 0 получим из (43) выражение:

д 5

i К-- iha ₃ Т7 W j , t 0.

. ⁹_t 3 _j

Уравнение (44) является полным аналогом (1 + 1) – размерности уравнения Дирака для безмассовой частицы m 0 в (18).

Из формы уравнений ФКГ имеем c cos 0 mc2 2 1 cos 0 . Отметим, что при 6 =0 и m 0 имеем максимальную скорость распространения волновой функции c 1 , что находится в согласии с требованиями релятивистской механики: масса частицы света равна нулю, а динамика квантового блуждания частицы с состояниями 0 и 1 распространяются независимо друг от друга по оси без интерференции с максимальным значением вариации.

Реализация квантовых случайных блужданий возможно на основе применения чип с квантовой фотоникой.

На рис. 12 приведена схема силиконового чипа на квантовой фотоники длиной 2.4 см для реализации управляемых квантовых ячеек ¹³ .

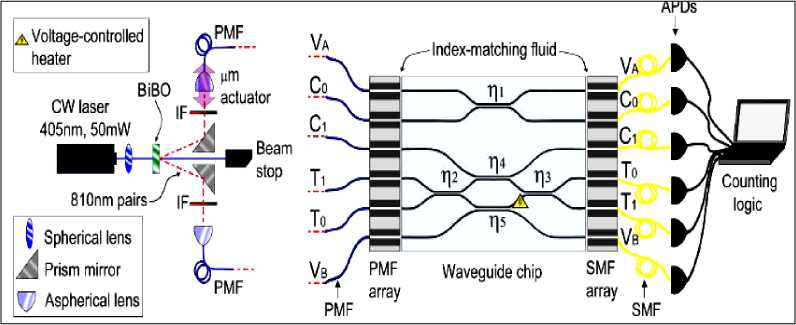
Рис. 12. Конфигурация чипа на квантовой фотонике

Реализация квантовых случайных блужданий для моделирования прототипа решений квантовых уравнений приведена на рис. 13.

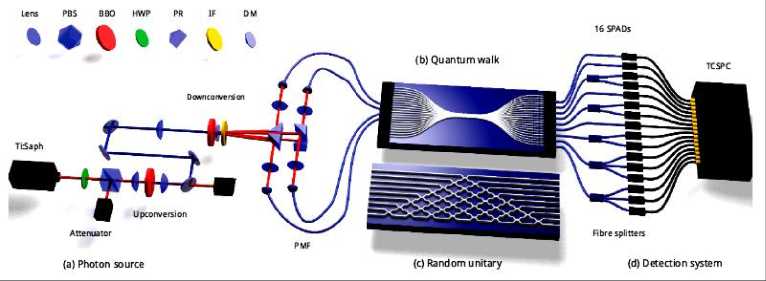
Рис. 13. Схема реализации квантовых случайных блужданий (а) – генератор фотонов;

(в,с) – интерференция и (д) – регистрация фотонов

На рис. 14 приведены результаты моделирования и сравнения с операциями случайных унитарных операторов (случайных унитарных матриц Хаара размером 99), показывающие удовлетворительные результаты применения технологии вычислений на основе квантовых случайных блужданий ¹⁴ .

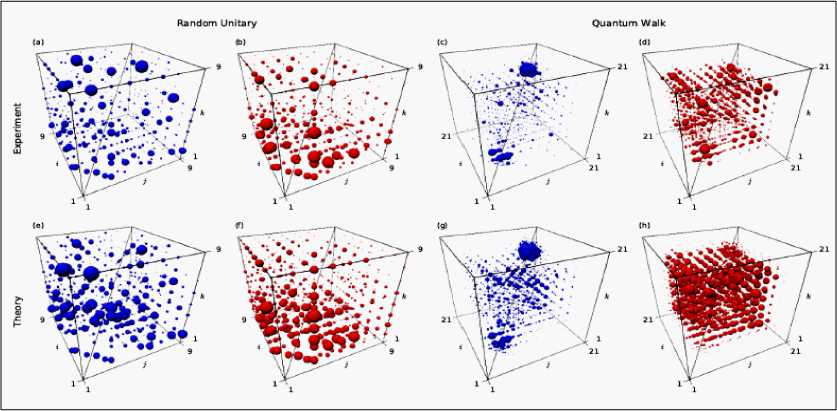
Рис. 14. Результаты моделирования девяти мод случайных унитарных матриц и 21 моды квантовых случайных блужданий

Рассмотрим кратко одно из применений уравнения Дирака в квантовой информатике: квантовый клеточный автомат Дирака. Клеточный автомат является ярким примером исследования интеллектуальных систем и имеет большие приложения как новая парадигма разработки моделей сложных систем в самых различных областях. Идея воспроизведения эволюции макроскопических систем на основе простого правила локального взаимодействия их элементарных составляющих была сформулирована фон Нёйманом под названием «клеточный автомат». Рассмотрим более подробно структуру квантового клеточного автомата Дирака и его влияние на исследования основ самой теоретической физики. Приложения квантового клеточного автомата Дирака более подробно освещены в Части 5 данной работы.

Пример 10: Квантовый клеточный автомат Дирака – Вейля и уравнение Дирака. В упрощенном виде автомат представляет собой регулярную решетку с ячейками (клетками) с конечным числом состояний. Состояние формируется по простому правилу: клетка из определенного состояния в момент времени t переходит в другое определенное состояние в момент времени t + 1 . Такое правило должно обладать локальным свойством, т.е. состояние клетки x в момент времени t +1 зависит только от состояний конечного числа близлежащих клеток в момент времени t .

Рассмотрим некоторые особенности применения квантовых релятивистских эффектов, которые используются для повышения эффективности применения клеточных автоматов [16 - 18]. В качестве примера обсудим применение уравнения Дирака для построения квантового клеточного автомата с позиции квантовой теории поля и его использование для решения важных задач квантовой информатики, теории интеллектуального управления и основ самой теоретической физики.

– Модель квантового клеточного автомата на основе уравнения Дирака . В квантовой теории поля унитарная эволюция поля ^ x сN числом внутренних степеней свободы описывается следующим образом:

уt + 1 U ^†^ t U ,   ^x = Vx x

.

я=1, ,N ’

Состояние квантового клеточного автомата, которому соответствует одно состояние поля (45), описывается унитарной матрицей U , которая действует линейно на оператор поля у/ как:

у/ t +1U уt , уX

у/ x , t

где x Е Z и t G Z , которые используются для обозначения нумерации безразмерной клетки (ячейки) решетки и шага времени соответственно.

На рис. 15 показан автомат (46), где световым конусам соответствует локальная структура эволюции автомата, а для каждого состояния x Е Z решетки существуют N систем, соответствующие внутренним компонентам поля.

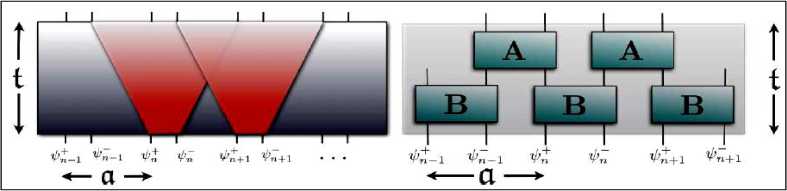
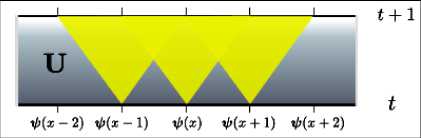
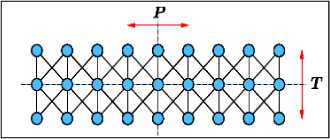
(а)                                          (б)

Рис. 15. Геометрическая модель одномерного квантового автомата Дирака с унитарным оператором блуждания (а); топология причинно-следственной сети квантовых блужданий (б)

Каждой клетке x решетки соответствует эволюция волновой функции ^ x поля. Оператор поля для клетки x взаимодействует с полем Vx + 1 близлежащих клеток. В случае автомата Дирака полевой оператор имеет две компоненты. Например, для одномерной решетки обобщенный инвариант преобразования квантового клеточного автомата с взаимодействием с близлежащими клетками можно представить в следующем виде:

U = RS + LS ^† + M ,                                 (47)

где S означает оператор сдвига S^ x = у/ x + 1 и R , L и M являются матрицы размерности N × N и не зависят от размерности решетки, инвариантны при преобразованиях.

Унитарность оператора U означает выполнение следующих условий: RR ^† + LL ^† + MM = I , MR ^† + LM ^† =0, LR ^† =0.

Автомат Дирака как квантовый клеточный автомат минимальной размерности удовлетворяет следующим требованиям: 1) унитарность эволюции; 2) гомогенность топологии взаимодействий; 3) инвариантность к обратимому преобразованию tt ; 4) инвариантность при четно преобразовании xx ; 5) минимальная размерность неидентичной эволюции.

Первые два требования уже содержатся в самом определении квантового клеточного автомата.

Требования 3) и 4) отражают симметрию топологии причинно-следственных сетей (см. рис. 15,б) и соответствуют рассмотрению сети как не раскрашенной (без петель). Предположение о взаимодействии с близлежащими клетками не является явным, так как всегда можно свести данное предположение к варианту простой составляющей автомата. Поэтому достаточно предположения о минимальности автомата. В уравнениях поведения автомата предположения 3) и 4) соответствуют следующим условиям:

TUT ^† = U ^† , PUP ^† = RS ^† + LS + M , (49)

где T – антиунитарный оператор и ассоциирован с обратимым преобразованием времени, P -унитарный оператор преобразования отображения симметрии на решетке.

Отметим, что член PUP ^† не изменяет свой вид как оператор U при замене оператора S на S ^† . При N = 1 только один оператор преобразований квантового клеточного автомата удовлетворяет четной инвариантности – оператор идентичности U = I . Для случая N = 2 из (49) следует, что операторы R и L унитарно эквивалентны, а из (48) следует, оба имеют ранг 1.

Таким образом можно выбрать базис в виде:

R

a

a

0 ) ,

уx

R ^x

L ^x

и имеет две компоненты поля XJ/_Rx и _L x – составляющая движения «вправо» и «влево»

соответственно. Тогда операторы P и T принимают следующий вид:

к1

0J

TC к1

0J

где C – анти-унитарный оператор комплексной конъюнкции. Данный выбор базиса в (49) дает

PRP ^†   L

и PMP ^†   M и получим следующие условия:

где a_i € C для i 1,  ,4. Из условия инвариантности и обратимости времени (49) следует, что

TRT†   L† и TMT†   M† . Из данных условий следует, что |a2 a2  1 Re a a 0, что с точностью до фазового множителя приводит к унитарному оператору U квантового клеточного автомата следующего вида:

nS im im  nS†

n2m21.

Постоянные n и m могут быть положительными величинами. Ограничение унитарности n ² m ² 1 в (53) приводит к условию на выбор параметра m в виде m Е 0,1 . Сам параметр m выполняет роль безразмерной массы инерции, а параметр n является аналогом индекса симметрии вакуума. Для перехода к обычному уравнению Дирака используются параметр длины ℓ и времени

Планка как параметры преобразования для пространства – времени, в котором роль массы играет масса Планка m . Максимальная скорость света распространения локального состояния в размерном пространстве - времени равна е = lp I тр . Величины 1р, тр и mp являются тремя универсальными фундаментальными параметрами, определяющие размерность L T и M , через которые определяется четвертая фундаментальная постоянная Й = mpIре .

Автомат для случая m 0 соответствует уравнению Вейля и называется автоматом Вейля.

На рис. 16 представлены результаты моделирования эволюции автомата [16] для локального состояния, решение отсутствует в квантовой теории поля, и для гладкого решения, типичного для квантовой теории поля.

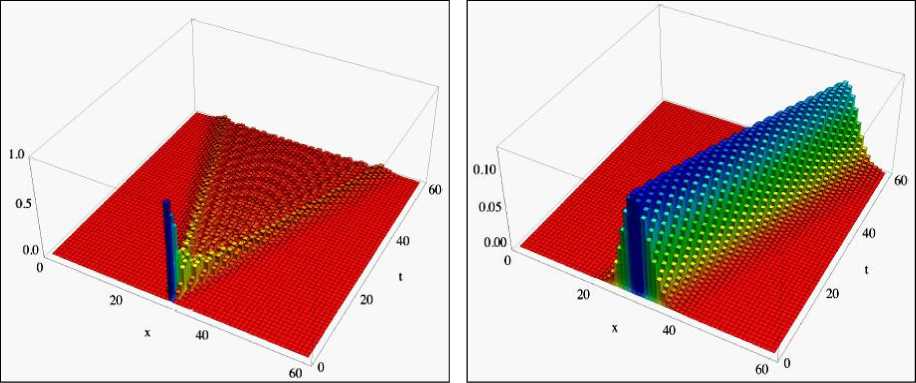
Рис. 16. Результаты моделирования эволюции автомата для локального состояния (а), и для гладкого решения (б)

Отметим частные случаи (46) и (53). Так, например, соответствующая (53) унитарная матрица

для одномерного автомата Дирака может быть представлена в виде:

U

nS im

im nS ^†

и оператор сдвига S x     x 1 состояния влево приводит к уравнению Шредингера:

.5 2 .

i        x, t

t

s

iv         D          x, t ,     x, t       x, t e x 2    x2

i k0x    k0t

где    k0   – дисперсия автомата,    x, t – амплитуда вероятности суперпозиции, s 1,

v k ,m

ⁿ       , D k ₀ , m

1 m ²cot² k

nm ²cos k

sin² k m ²cos² k ²

Для двумерного случая d 2 унитарная матрица автомата имеет следующий вид:

где       1 и S _xy   S _x   S ^† _y с оператором сдвига

S в направлении    топологической сети с

взаимодействующими клетками.

На рис. 17 представлены результаты моделирования двумерного автомата Дирака (57) [17, 18] в различных режимах.

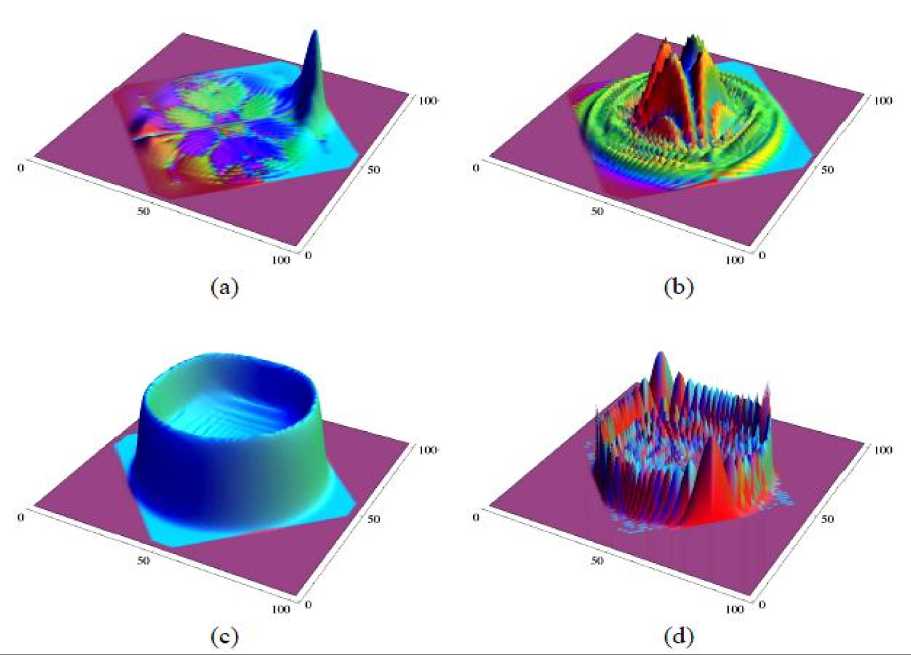
Рис. 17. Поведение двумерного автомата Дирака при различных начальных условиях

Амплитуде представленных на рис. 17 графиков соответствует вероятность найти состояние частицы со спином Ѕ ( ф – направленного вверх) через 45 интервалов времени т Планка для различных начальных условий. На рис. 17,а начальное условие – Гауссовский волновой пакет с A__y = А_>; = 2I (минимальной неопределенности) и соответствует высокому релятивистскому моменту; рис 14,b соответствует ультрарелятивистский момент в ограниченной зоне Бриллюэна; на рис. 17,d начальное состояние локализовано как простая планковская ячейка; рис. 17,c,d. соответствует нулевой момент.