Квантовая релятивистская информатика. Ч. 4: элементы квантовой релятивистской теории информации и квантового программирования
Автор: Ульянов Сергей Викторович, Албу Вячеслав Андреевич, Бархатова Ирина Александровна, Решетников Андрей Геннадьевич, Ростовцев Виталий Александрович
Журнал: Сетевое научное издание «Системный анализ в науке и образовании» @journal-sanse
Статья в выпуске: 4, 2013 года.
Бесплатный доступ
Рассмотрены алгоритмические и физические особенности основных моделей квантовых операторов, применяемых при конструировании квантовых алгоритмов. Моделирование квантовых алгоритмических ячеек рассмотрено с позиции квантового программирования. Кратко описаны основные языки квантового программирования и факты квантовой релятивистской теории информации.
Квантовые операторы, квантовое программирование, квантовая релятивистская информация, квантовая релятивистская информатика
Короткий адрес: https://sciup.org/14123234
IDR: 14123234
Текст научной статьи Квантовая релятивистская информатика. Ч. 4: элементы квантовой релятивистской теории информации и квантового программирования
QUANTUM RELATIVISTIC INFORMATICS.PT. 4: ELEMENTS OF QUANTUM RELATIVISTIC INFORMATION THEORY AND QUANTUM PROGRAMMING
Ulyanov Sergey1, Albu Veaceslav2, Barchatova Irina3, Reshetnikov Andrey4, Rostovtsev Vitaly5
-
1Doctorof Science in Physics and Mathematics, professor;
Dubna International University of Nature, Society, and Man,
Institute of system analysis and management;
141980, Dubna, Moscow reg., Universitetskaya str., 19;
-
2 J unior scientist ;
Institute of Mathematics and Computer Science;
Republic of Moldova, Chisinau MD 2028, Kishinev, Academiei str.5;
-
3Senior researcher;
Dubna International University of Nature, Society and Man,
Institute of system analysis and management;
141980, Dubna, Moscow reg., Universitetskaya str., 19;
-
4PhD student;
Dubna International University of Nature, Society and Man,
Institute of system analysis and management;
141980, Dubna, Moscow reg., Universitetskaya str., 19;
-
5Associate professor;
Dubna International University of Nature, Society and Man,
Institute of system analysis and management;
141980, Dubna, Moscow reg., Universitetskaya str., 19;
Введение: Роль квантовой релятивистской теории информации и квантового программирования как фундаментального базиса квантовой релятивистской информатики
Разработка наукоёмких ИТ затрагивает одновременно пересмотр исходных положений таких фундаментальных теорий как квантовая механика, общая теория квантовой гравитации, квантовой релятивистской термодинамики, теории неразрушающих квантовых измерений в криволинейном пространстве – времени, квантовой релятивистской теории описания поведения релятивистской частицы в римановом и неримановом пространственно-временном континууме и мн. др.
В свою очередь, существование алгоритмической неразрешимости при применении традиционных вычислительных методов и количественных подходов к поиску оптимальных решений сложных задач физики, механики, биофизики, систем управления, развитие наукоемких компьютерных (типа квантового компьютера) и прорывных ИТ типа квантовый Интернет на основе квантовых слепых облачных вычислений (quantum blind cloud computing), квантовая криптография, квантового управления наноструктурами, формирования интеллектуальных наноматериалов, разработка ИТ нанотехнологий и мн. др. привело к необходимости поиска и развития технологий на основе новых видов интеллектуальных вычислений (ИВ) и программно-аппаратной поддержки вычислительных процессов.
Разработка подобных наукоёмких платформ элементной базы аппаратной поддержки квантовых ИТ потребовало одновременно создания и внедрения новых видов нанотехнологий изготовления материалов и технологической оснастки. Резко возросший объем перерабатываемой информации и сложность решаемых задач в науке и технике привел к необходимости создания новой элементной базы квантового компьютера, способного реализовать квантовый массивный параллелизм обработки информации, решать классические алгоритмически неразрешимые задачи с экспоненциальной скоростью, обладая огромной памятью и быстродействием.
Поэтому выбранное решение фундаментальных и прикладных проблем конкретной технологии ИВ существенно влияет на эффективность разработки и качество применения моделей наукоемких ИТ. Возрастание сложности структур современных физических объектов и логических устройств, трудности прогнозирования непредвиденных (нештатных) ситуаций управления только усиливают актуальность данной проблемы и внимание к поиску её решения.
Элементы квантовой релятивистской теории информации
В данном разделе рассмотрим кратко некоторые особенности и прикладные аспекты квантовой релятивистской теории информации с позиции системной инженерии и задач квантовой релятивистской информатики. Прежде всего, остановимся на некоторых мерах количества информации и оценки влияния квантовых и релятивистских эффектов на измерение количества информации.
Меры квантовой информации и законы квантовой теории информации
Информационная энтропия Шеннона определяется как H p = -^p z log pz .
i
Энтропия фон Неймана имеет следующий вид: SvN р т-Tr plogp .
В частном случае, когда матрица диагональная, наблюдается тождественное равенство энтропийных мер Шеннона и фон Неймана. Однако законы и следствия квантовой теории информации имеют ряд принципиальных отличий при квантовом обобщении классической теории информации Шеннона.
– Меры информации Фишера / Шеннона и информационные метрики пространства – времени
В данном разделе рассмотрим прежде всего простые примеры вывода широко применяемых мер информационной энтропии Шеннона и количества информации Фишера.
Информационная энтропия Шеннона . Напомним, что само понятие «информация» в теории Шеннона не ассоциируется с индивидуальным сообщением, а характеризует источник сообщений. Идея о статистической природе источника позволяет упростить описание пропускной способности канала передачи информации, воспроизводимой источником сообщений. Рассмотрим ансамбль X = x , x 2,.. .xn алфавита xt , появляющегося в сообщении с вероятностью p x{ . Ансамбль сообщений состоит из большого числа N . Для каждого сообщения типовая последовательность букв алфавита x содержит Np x букв, Np x , из x и т.д.
Число таких различимых типовых последовательностей букв сообщений определяется
N !
комбинаторикой как и применяя формулу Стирлинга получим
Np хг ! Np x2 !.. Np xn !
n аппроксимацию данного выражения в виде 2 NH X , где H X = p x log p x является
i информационной энтропией Шеннона. При N —> 00 вероятность появления нетипичной
NH X последовательности стремится к нулю и поэтому достаточно рассматривать типовой ансамбль 2 типовых равновероятных типовых последовательностей сообщений.
Таким образом, ансамбль из N букв алфавита может быть сжат до NH X N log n бит (теорема о сжатии Шеннона).
Соотношение неопределенности и информация Фишера. Рассмотрим процесс измерения координаты x для упрощения в одномерном пространстве. Результат многократного измерения данной величины можно охарактеризовать средними значениями как x xp x,t dx, x2x2p x,t dxp , где интегрирование осуществляется по всему пространству значений измеряемой величины и p x,t 0 при условии нормировки функции плотности распределения вероятностей p x,t 1 и lim xnp 0, n 0,1,2 . Проинтегрируем по частям условие нормирование функции p x,t 0 и x p получим xp х = -00 “ x dx 1 .
x
Примем за нулевое значение первый член, согласно ранее принятому предположению и получим
1 I I 1 сp условие x dx 1 . Положим теперь, что u x p и.
xpx
Из известного неравенства Шварца u , u S , i9 > | u , <9 | u , <9 J u <9 dx получим соотношение
1 /2
«неопределенности» в виде x 2 I 1, где I p dx и называется информацией Фишера.
px
Соотношение между дивергенцией, информационной энтропией Шеннона и количеством информации Фишера . Допустим, что X является случайной величиной с заданной (в общем случае не гауссовской) плотностью распределения вероятностей и конечной величиной дисперсии. Пусть d
XX+ ^tZ , где Z случайная величина, имеет стандартное нормальное распределение, независи- мое от X . Тогда имеем следующее соотношение между информационной энтропией Шеннона и количеством информации Фишера1:
HX
1 log 2 Лe I X dt .
2 2 t 1+ t .
Обозначим относительную энтропию (расхождение Кульбака-Леблера) для плотности вероятностей px относительно нормальной qx с тем же средним значением и дисперсией как и у px
в виде S X = p x log
px qx
dx . Относительная энтропия не симметричная функция и
поэтому не обладает свойством метрики (расстояния), а измеряет отклонение px от qx . Если среднее E X f и var X = (72 , то имеем:
SX = J p x log p x dx - J p x log q x dx H X - j px
1 xa
7 2 TIG 22 c 2
dx
=1 [ log 2 TIG 2 +1
Таким образом, относительная энтропия определяет отличие информационной энтропии Шеннона случайной величины X от нормального закона. При px равном qx величина SX равна нулю, т.е. нормальное распределение имеет при заданной дисперсии максимальную величину. Для случайной величины X с определенными ранее параметрами обобщенная стандартная мера количества информации Фишера определяется как: 2
pX qX pX qX
Ф X = G 2E
и SX 11 ф v tX + 1 tY dt .
2 t
Тождество de Bruijn определяет соотношение между энтропией Шеннона и количеством
. - 8 1
информации Фишера в виде: h X + ^tZ I X + -x]tZ , где he = - f p x ln p x dx означает
9te 2 e дифференциальную энтропию Шеннона по основании e . В частном случае в пределе t 0 имеем из
d приведенного выражения h X + VtZ 5te
1 IX .
t 0 2
Тождество de Bruijn для дивергенции Кульбака – Леблера и относительной информации Фишера d1
имеет вид: S p q= —Ф dt 2
p I q . Для меры относительной энтропии Реньи типа:
DP II Q
1 -a
log ( QP
dP ,
а > 0, P □Q
имеем dD d3 c
P II Q l„ 0
-f4 v log
2 pz qz
p z q1 z dz
£ p u q 1 u du
при условии lim_^_r p z q 1 z 1 =0.
z dz
Для более обобщенных мер типа I P
имеет место соотношение 2 :
dI d f
P II Q
5= 0
1 2 q yf
py qy
py qy
dy .
Имеет место соотношение
dS
—
dt dt2
Тогда имеем:
St 0 St St 0 + t t 0 I t 0.
Информационная геометрия. Рассмотрим некоторые примеры:
Пример 1: Квантовые геометрические аналоги классических моделей кривизны в информационной геометрии искривленных пространственно-временных континуумов . Рассмотрим в качестве примера факты геометрии пространства квантовых состояний. Расстояние между двумя квантовыми состояниями \vt и W2 можно определить различными способами (V. V. Dodonov, O. V. Man’ko, V. I. Man’ko, A. Wunsche, Phys. Scripta 59, 81 (1999)). Например, широко применяемые меры расстояния Fubiny-Study (FS) и Woo tters (W) опр еделяются соответственно в следующем виде:
d FS IV1,2 1-|(^12)l2 и dW 1^1),V2) = arccos y\^12)l , где у – постоянная величина. Несмотря на внешнее различие, данные меры расстояния эквивалентно определяют расстояние между квантовыми состояниями. Так для близких состояний, когда 1221-32 , где 6 – малая величина, имеем соотношение dFS dW = y5 . Аналогичным образом определяются другие меры расстояний (см., ниже). Аналогично данному результату элементы длины для семейства (множества) векторов квантовых состояний |^ ^1, 2, ,^k параметризованных k параметрами § 1,^2, ,§k , определенные на заданных метриках расстояния, эквивалентны для различных определений расстояния ds 2 g d§id j с метрическим тензором:
gij =y 2 Re ^iVji I^X^I^7 j , где \vii -|^ ^1, 2, , k .
Приведенная форма метрики расстояния применяется на практике многими исследователями и обычно принимается y-2 . Тогда для двумерного случая g является метрическим тензором сферы с единичным радиусом (сфера Блоха). При рассмотрении эволюции квантового состояния, описываемой уравнением Шредингера, вводится понятие скорости квантовой эволюции ds = -xK H 2 , где H H -(H ) . dt,.
Рассмотрим теперь определение геодезической кривой на пространстве векторов квантовых состояний. Геодезическая линия (однопараметрическое множество векторов квантовых состояний), соединяющая два вектора состояний 1^ и V t можно определить как линейную комбинацию (аналог суперпозиции):
к ^ )= C 1 01 ei , (1)
где § – параметр, принимающий значения от 0 до 1.
Примечание 1. Фазовый множитель eiФ выбирается следующим образом. Векторы 1^ и ei 0 определяют эквивалентные квантовые состояния. Поэтому требуется выполнение условия эквивалентности геодезических линий определенных между состояниями 1^ и\v J , и состояниями ei 0 и w I ei 1 . Данное условие выполняется, если выбрать eiф = 10. Условие нормализации для параметра C определяется из выражения внутреннего произведения (^ § V ^ )=1 и имеет следующий вид: C . Отметим, что геодезическая линия (1) является
12^1-^ 1 -l(^10
множеством состояний и существует много способов её параметризации. В геометрии квантовых состояний показано, что длина кривой в квантовом пространстве состояний не зависит от пути её параметризации.
Для вычисления длины геодезической линии удобно представлять определяющее её уравнение в виде:
V ^ VC
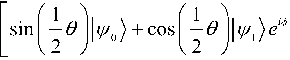
где новый параметр 0 <6 <71 и константа нормализации C .
-
1 +|(^10)| sin 6
Подчеркнем, что (1) и (2) адекватно описывают однопараметрическое семейство векторов квантовых состояний в виде геодезических линий.
Используя определение метрики как: g -у 2Re ^ i I ji к)(^к j для
Л А У 1 Ч(^10II 2
однопараметрического множества состояний дает выражение ds.
21+ 1^10)| sin
Тогда длина геодезической линии, соединяющей состояния W и V т ) , определяется в виде:
s ds = у arccos |(^10.(3)
Таким образом, выражение (3) для длины геодезической линии совпадает с выражением метрики Wootters расстояния между векторами квантовых состояний. Аналогично можно вычислить длину кривой (1), соединяющей состояния V и1^ т ) , для определенной фазы ф . Тогда геодезическая линия определяется как кривая минимальной длины на семействе кривых.
Минимальная длина достигается при установленном выше условии eiф = 10 и эквивалентно метрике расстояния Wootters.
Рассмотрим теперь другой геометрический фактор – кривизна пространства и его квантовый аналог в пространстве векторов квантовых состояний.
– Кривизна. Вектор состояния квантовой эволюции от одного параметра, такой как время t , и однопараметрического множества векторов состояний 1^ t= exp iHt 1^ , генерируемое гамиль тонианом системы. Отклонение вектора состояний 1^ t от геодезической линии, связывающей состояния WиV 1 ^ , определяется через кривизну пространства. Для введения понятия кривизны рассмотрим случай эволюции из двух состояний 1^ в \v1 . На первом этапе предположим, что осуществляется эволюция в течении отрезка времени Аt из начального состояния 1^ в промежуточное состояние 1^^ в виде 1^') = e к 1^ 0 ) и далее в течении отрезка времени А t из состояния 1^^ в iHАt iH Аt +Аt состояние W1ee0, где H – не зависящий от времени гамильтониан. Без потери общности в дальнейшем принимается Аtt. Отклонение квантовой эволюции от геодезической линии, связывающей состояния 1^ иV 1 ^ , может быть охарактеризовано максимальным значением величины 1^'к ^ )|2 параметризованной § . При max 2 1 состояние 1^^
принадлежит геодезической. Отклонение 1^^ от геодезической увеличивается с уменьшением величины max1^'к ^ )|2 , соответственно. Обычно вводится следующее выражение
-
1 max 2 min 1 -К^'к ^ )| , которое эквивалентно нулю, когда отклонение равно нулю,
и положительно возрастает, когда отклонение увеличивается.
Нетрудно заметить, что данное выражение эквивалентно метрики расстояния Fubiny-Study.
Пример 2. Рассмотрим теперь уравнение геодезических в рамках квантовой геометрии с обобщением понятия в квантовых системах отсчета. В этом случае рассматривается 8-мерное фазовое пространство xЦqr , ps , q 0 ct ; p 0 E / c , метрикой ds 2 типа:
ds 2 dt 2 2 x 2 4 6 2 dE 2 dp 2
c 2 4 c 6 c 2
1 a 2 2 c 2
описывает пространство-время квазиклассического уровня с
где E mc m c m c , A
2 A2 m h ограничением на максимальное собственное ускорение a для частицы в виде величины A , полученной из квантовых ограничений. Пространство-время, описываемое метрикой (9), является 8-мерным: первые четыре компоненты образуют пространство-время, описываемое 4-вектором xA = t, x / c ,ц-0,1,2,3 ; вторая группа 4-компонент, ортогональных к первой группе xM , про- порциональна 4-скорости
cdx ц f c 5 )
u, dT v^1-s2 /c2 ,1 2 /c2
u 0, u . Событие в метрике (4)
описывается 8-компонентами 5м =t,x/c;w0,w , w0u0/k, w u /k , где к – нормирующий пара- метр. В этом случае 8-мерный пространственно-временной континуум определяется в виде:
gd d^v =dt 2 dx / c 2 dw 0 dw 2 .
В этом случае преобразования Лоренца для (5) принимает обобщенный вид:
dt dt 0 dx a 0 0 dw 0 a 0 dw 1
г
c
ck
k 1
; dx
г
dt dx a 0 cdw 0 a 0 dw 1 ;
0 k 2 k 0
dw 0
г
0 a 0 dt a 0 dx dw 0 0 dw 1 ; dw 1 a 0 dt 0 a 0 dx 0 dw 0 dw 1 ;
ck
ck
c
г
k
c 2 k
1 c
; (6)
г =
Q 2
1 0 2
a 0
,
( а 2> 3/2
k 1 k 1 0 2
a 0
2 a 2 m 0 c 2 .
При г9/ c 1 и c / k 1 имеем E m c 2 + — m i9 ч—
Уравнение геодезических (как частный случай обобщения для квантового параллельного переноса) имеет вид:
x“ + iFЗх xРx 0, ,
где связность i F задается в виде: F p dq
Г Л 0
qrdp
, г, = diag 1,1,1, 1 . Уравнение (7)
для x ^ = qr , ps при заданном F распадается на систему уравнений:
ql +ipsqsql 0; pl ipsqspl 0 . (8)
Если ввести обозначения z q ip, z q+ ip , то из (13) при § = zk,zk xk iyk,аk— уk+i со k имеем уравнение диссипативной системы:
xk + /xk -toyk 0; yk + уyk + гоxk 0 (9)
в виде системы связанных осцилляторов.
Свойства количества классической и квантовой информации .
В табл. 1 приведены основные свойства классической и квантовой мер информации, применяемых в решении задач информационного анализа и проектирования квантовой эволюции.
Одними из основных проблем квантовой теории информации, решение которых важно для исследования квантовой эволюции динамических систем, являются следующие:
Таблица 1. Свойства классической и квантовой информации
|
Теории информации |
|
|
Классическая |
Квантовая |
|
Энтропия Шеннона : HX =-Е px log px x |
Энтропия фон Неймана : S р =-Tr р log р |
|
Различимость и доступность информации |
|
|
Знаки алфавита различимы : NX |
Граница Холево - Левитина : H X : Y S pxS x , ^=Е px рx |
|
Информационно – теоретические отношения |
|
|
Неравенство Фано : H pepe log I X |-1 HX I Y |
Квантовое неравенство Фано : HF р , E +1 Fр , E log d 2 1 S р , E |
|
Взаимная информация : H X : Y H Y H Y X |
Когерентная информация : Iр , E S E S , E |
|
Неравенство цепи обработки данных : XYZ H X H X : Y H X : Z |
Квантовое неравенство цепи обработки данных : р^ E1 р E2 ° E1 р Sр Iр ,E1 I ,E2 0 E1 |
|
Кодирование канала передачи данных без шума |
|
|
Теорема Шеннона : n H X |
Теорема Шумахера : n S Е px рx x |
|
Пропускная способность каналов связи с шумом для классической информации |
|
|
Теорема Шеннона кодирования канала связи с шумом : C N max H X : Y px |
Теорема Holevo-Schumacher-Westmoreland : C 1 E max S р' -^pxS x , p j , j x рx E рx , px рx x |
Классическая, квантовая и полная корреляции: Взаимосвязь с мерами запутанных состояний;
Доступная информация и информационно-теоретические модели квантовых измерений;
Извлечение информации эффективными измерениями и границы взаимной информации.
Исследуем кратко на примерах некоторые из этих особенностей, используемые в моделях квантового нечеткого вывода (КНВ).
Пример 3 . Рассмотрим особенности описания и информационного анализа запутанных 0 1 0 0 1 1 1 0
состояний Белла 14х 1 0 1 0 . Так как состояние Белла с оператором плотности чистое, то р представляет чистый ансамбль. Поэтому неопределённость квантового состояния отсутствует, т.е. энтропия фон Неймана SvN р 0.
Редуцированный оператор плотности р для квантового бита I 0 есть частный след над системой Q , т.е.
р 0 Tr 1 рQ 1 2 0 0 1 1 1 2 1 01 0
Следовательно, квантовая
неопределённость в состоянии I 0 определяется энтропией фон Неймана как SvN р 1.
Таким образом, информационный анализ неопределенности в состоянии составной квантовой системы позволяет четко разъяснить наличие необычных (неклассических) свойств: игнорирование в
Электронный журнал «Системный анализ в науке и образовании» Выпуск №4, 2013 год ней части информации о состоянии подсистемы приводит к увеличению квантовой неопределённости.
В результате квантовая неопределенность в «части» (подсистеме) Q больше, чем в «полной» (составной) квантовой системе Q . Такой эффект отсутствует в классических системах в силу свойств меры информационной энтропии Шеннона.
Пример 4 . Рассмотрим состояние Белла w\
00 ) + l11} в Гильбертовом пространстве
J 2
HH®H , где HHH. Матрицы плотностиp AB =ии ,p,p определяются как:
pA
|
(1 |
0 |
0 |
1 |
2 |
0 |
0 |
2 |
|||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||
|
1 |
, pA | B |
0 |
0 |
0 |
0 |
, pAB |
0 |
0 |
0 |
0 |
|
2 J |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
||
|
V 2 |
2J |
.
Матрица условной плотности pA | B — pAB (I A ® p ) 1 (в этом случае взаимная p и маргинальная I матрицы плотности коммутируют). Из определения энтропии фон Нёймана следует S vN ( A ) S vN ( B ) 1. Тогда S ( AB ) S ( B ) + S ( A | B ) 1 1 0 , так как S ( A | B ) 1.
Следовательно, в отличие от классической теории информации Шеннона квантовая условная энтропия фон Неймана может принимать отрицательные значения, когда рассматриваются запутанные состояния. Этот факт непосредственно связан с квантовой неразделимостью запутанных состояний, а сами они интерпретируются как гигантски (супер) коррелированные состояния. Таким образом, отрицательность условной энтропии указывает на наличие запутанных состояний в составной квантовой системе и определяет нижнюю границу их корреляции.
Существование данного факта установлено также в квантовых поисковых алгоритмах Шора и Гровера и используется в решении проблемы эффективного останова КА.
Отметим также, что не все базовые классические соотношения и неравенства имеют квантовые аналоги. Так, например, в классическом случае I ( x : y ) min H ( x ), H ( y ) .
Тогда как в квантовом случае верхняя граница задается неравенством:
S ( X : Y ) 2min S ( X ), S ( Y ) .
Квантовая теория информации имеет строго обоснованные правила, как извлекать информацию из неизвестного кантового состояния. Оптимальный квантовый процесс извлечения ценной информации из индивидуальных БЗ, спроектированных для фиксированных ситуаций управления на основе мягких вычислений, основан на четырех фактах квантовой теории информации, приведенных ниже. В частности, доказано, что существует: эффективное квантовое сжатие данных; «сцепление» классической и квантовых частей информации в квантовом состоянии; полная корреляция в квантовом состоянии является «смесью» классической и квантовой корреляций; наличие скрытой (наблюдаемой) классической корреляции в квантовом состоянии. Далее кратко рассматривается физический смысл перечисленных фактов и их роль в процессах проектирования оптимальных процессов и сигналов управления на основе КНВ.
Факт 1. Эффективное квантовое сжатие данных. В классической теории информации Шеннон показал, насколько (при заданной точности) предельно можно сжать сообщение, состоящее из N независимых знаков x , где каждый знак появляется в сообщении с априорной вероятностью p , используя понятие информационной энтропии. Информационная энтропия Шеннона Hp определяется как H p = p log p . Было доказано следующее утверждение: блок кодов длиной NH битов достаточен для кодирования всех типовых (наиболее часто появляющихся)
последовательностей без учета способов кодирования нетипичных последовательностей сообщений. При этом вероятность ошибки кодирования (потери информации) не превосходит заданный порог 8 . В квантовой теории информации знаками являются матрицы плотности. Возможны два варианта, когда матрицы плотности соответствуют ансамблю чистых состояний УФ^ или когда ансамбль формируется матрицами плотности р с вероятностью p . Рассмотрим ансамбль состояний для второго варианта. В этом случае матрица плотности сообщений, состоящих из N знаков, описывается как рN = р® р®---® р , где р=У,a pa \фaa I .
Энтропия сообщений фон Неймана S Tr р ln р имеет простое соотношение с энтропией ансамбля, S N NS р . Известно следующее неравенство между Шенноновской информационной энтропией и энтропией фон Неймана: H p S р , т.е. значение информационной энтропии Шеннона превышает значение энтропии фон Неймана. Это означает, что применение квантовой теории информации позволяет осуществить более глубокое сжатие классической информации.
Факт 2. Сцепление (разделение) информации в квантовом состоянии в виде классической и квантовых частей. Рассмотрим модель обобщённого измерения (см. разд. 2) на состоянии AA† , для i Ai BAi† которой матрица плотности имеет следующее определение: .
B Tr A р B A i †
Конечное состояние подсистемы B будет тогда AрA= pрi . Энтропия ii редуцированного состояния равна pS i . Количество классической информации, полученной на измерении i с вероятностью p выражается как информационная энтропия Шеннона Hp. Если квантовые состояния рBi принадлежат ортогональным подпространствам, то энтропия конечного состояния (после измерения) есть сумма редуцированной квантовой энтропии, ^ piS Bi и i классической информации т.е.:
S piр BiH p piS Bi .
i Классическая i
Квантовая
Таким образом, количество информации, содержащейся в квантовом состоянии, может быть разделено (сцеплено в виде) на квантовую и классическую части. Поэтому при моделировании робастных структур ИСУ с помощью ОБЗ моделируется классическая часть информации, а ее дефицит может быть определён как:
А IS [z piр BipiS BiHp .
-
ii Классическая
Полная Квантовая
Можно извлечь, следовательно, дополнительное количество ценной квантовой информации из индивидуальных БЗ для последующего использования при проектировании интеллектуального управления повышенного уровня. При этом применяются квантовые процедуры сжатия и редукции избыточной информации, содержащейся в классических сигналах управления (привлекая соответствующие модели квантовой корреляции в квантовом алгоритме КНВ).
Факт 3. Количества полной, классической и квантовой корреляций. Запутанные состояния или, в общем виде, квантовая корреляция являются типичными физическими ресурсами квантовых вычислений. Однако не все виды корреляций имеют чисто квантовую природу. Иными словами, полные корреляции представляют собой «смеси» классической и квантовой корреляций. Для оптимального проектирования (эффективно моделируемых на классических компьютерах) заданного класса КА важно знать тип (и вид) необходимой классической корреляции. Так, например, если возможно определить классическую часть корреляций, то, используя оптимальные ПООЗ-меры измерения, допустимо извлечь максимальное количество информации в классической форме, содержащейся в квантовом состоянии, с минимумом возрастания энтропии. Количество полной корреляции может быть разделено на классическую и квантовую части. Данная мера эквивалентна мере максимальной классической/квантовой взаимной информации I A : B , сохраняя непосредственно прямую физическую интерпретацию взаимоотношений между соответствующими мерами.
Факт 4 . Скрытая (наблюдаемая) классическая корреляция в квантовом состоянии . В квантовой теории информации установлен следующий неожиданный факт. Условие пропорционального увеличения количества информации ICl р = max I A : B , определённого локальными
Cl MAMB измерениями MMна состояниир , может быть нарушено при некоторых экстремальных ограничениях на начальное смешанное состояние р . Так, например, начальный объем информации в виде одного классического бита информации, посланного от A к B, может увеличиться на этапе приема на определённую величину в количественной мере I р . Этот факт объясняется с позиции феномена наблюдения классической корреляции в квантовом состоянии р . Так как пропорциональное увеличение количества информации I р выполняется на классическом уровне, то феномен наблюдения корреляции является чисто квантовым эффектом, возникающим вследствие неразличимости квантовых неортогональных состояний.
Поэтому существуют квантовые двухчастичные состояния, которые содержат большое количество классической корреляции, ненаблюдаемой на классическом уровне из-за диспропорционально малого для ее наблюдения необходимого количества классической информации в канале передачи (ограниченная способность передачи информации).
Существует 2 n 1 квантовых битов, с помощью которых однобитовое сообщение вдвое увеличивает оптимальное количество классической взаимной информации как результат измерений между подсистемами. В общем случае для посланных n /2 битов происходит увеличение указанного количества информации до n битов. Получить указанный эффект на классическом уровне невозможно в силу законов классической физики. При этом замечателен следующий факт: состояния, поддерживающие указанный эффект, не обязательно должны быть запутанными и соответствующий классический канал обмен данными можно реализовать с помощью преобразования Адамара.
Приведенные факты составляют информационный ресурс основы КНВ, используемый при моделировании робастных БЗ для интеллектуальных НР.
– Полная корреляция и скрытая (наблюдаемая) корреляция в квантовых состояниях. Существует уверенность, что ожидаемая вычислительная мощность квантовых вычислений исходит из существования квантового ресурса. Запутанные состояния, или квантовая корреляция в общем случае, являются яркими тому примерами. Однако, как упоминалось в разд. 3, не все виды корреляции имеют чисто квантовую природу, т.е. полная корреляция представляет «смесь» классической и квантовой корреляций. Важным моментом является знание о том, как и где, используется классическая корреляция в КА. Например, если возможно определить и выделить классическую часть корреляции, то с помощью оптимального измерения можно извлечь некоторое дополнительное количество информации в классической форме, скрытое в квантовом состоянии, с минимальным возрастанием энтропии.
Физически перечисленные виды корреляции характеризуются количеством работы (шумом), которое необходимо совершить для устранения (разрушения) корреляций: для полной корреляции требуется количество работы до полного разрушения, для квантовой корреляции достаточно количество работы до разрушения на разделимые состояния. Однако и в случае классической корреляции максимальная корреляция разрушается после устранения квантовой корреляции. Полное количество корреляции, измеряемое минимальным производством рандомизации и эквивалентное требованию полного разрушения всех видов корреляций в состоянии р , эквивалентно квантовому количеству взаимной информации.
Классическая и квантовая корреляции . Классическую взаимную информацию, содержащуюся в квантовом состоянии рАВ (до его измерения), можно оценить естественным образом как максимальную взаимную информацию, которую можно извлечь путём локальных измерений MA ® Мв на состоянии рАВ :
In р = max I A : B .
Cl M A M B
Здесь I A: B - классическая взаимная информация, определяемая в виде: I A:B нН pa нН Рв нН Рав , где Н - информационная энтропия и pAв, pA, pB - функции плотности распределения вероятностей взаимного и индивидуального результатов, полученных локальными измерениями MA®MB на состоянии р.
Пример 5: Взаимная информация и классическая корреляция . Для понимания роли классической корреляции, а также её взаимосвязи с понятием взаимной информации, определим квантовую взаимную информацию для двухчастичного состояния рАВ квантовой системы в форме Стратоновича
I A : в sS рА sS Рв —S рАВ .
Рассмотрим составную систему AB в состоянии рАВ, способную пребывать в состоянии рА с вероятностью p и с вероятностью 1 - p - в другом состоянии рв . Для данного случая составной системы AB взаимная информация может быть вычислена в следующем виде:
I A : B
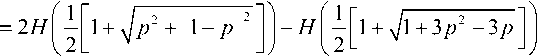
Если рАВ - разделимое состояние, то его относительная энтропия в запутанном состоянии равна нулю. Физическая интерпретация значения Icl р многозначна: Icl р выступает максимальной классической корреляцией, извлекаемой чисто локальной процедурой измерения из состояния р; Icl р соответствует классическому определению, когда состояние р - «классическое», т.е. диагональное в некотором (локально используемом) вычислительном базисе и отвечает классическому распределению; если р - чистое состояние, то Icl р задает корреляцию, определённую базисом Шмидта и эквивалентную мере перепутанных чистых состояний; Icl р = 0, если и только если рАВ = р^ рв .
Известно, что некоторые подходящие меры квантовой корреляции должны удовлетворять некоторым аксиоматическим свойствам: 1) квантовая корреляция является нелокальной и не может возрастать при локальных процедурах измерений (свойство монотонности); 2) полная пропорциональность; 3) приращение пропорциональности; 4) непрерывность по р .
Физически свойство 2) означает, что протокол состояний, составленный из некоррелированного начального состояния, использующий 1 квантовых битов или 2 1 классических битов (для передачи сообщений по квантовому каналу связи) и применяющий локальные операции, не может породить более чем 2 1 битов корреляции. Свойство 3) предполагает, что при передаче сообщения в количестве 1 квантовых битов или 2 1 классических битов корреляция в начальном состоянии не возрастает и не превышает величины 2 1 битов.
Свойства 1)-4) выполняются полностью для ряда известных мер корреляции. Эти свойства справедливы, в частности, для классической взаимной информации I A : B , когда передача сообщений осуществляется классическим способом. Так, например, свойства полной и приращения пропорциональности I A : B для классического случая следуют из факта, что max Н pA , Н pB НН pAB< Н pA + Н pB , так что когда А посылает классическую систему А'
к B , имеем Ia р =1 A;BA <1 АА ; B нН p^ .
Тогда свойство полной пропорциональности следует из свойства приращения пропорциональности. Это же выполняется для квантовой взаимной информации
I Q A : B Sр A +S р B Sр AB .
Неожиданным оказалось то, что свойство приращения пропорциональности нарушается для I р экстремальным образом в случае смешанных начальных состояний р : простой классический бит, посланный от A к B , может в результате привести к увеличению I р до некоторого большого значения.
Данный феномен рассматриваем как возможность наблюдения классической корреляции в квантовом состоянии р . Если свойство приращения пропорциональности I р имеет место на классическом уровне, то феномен наблюдаемой классической корреляции является чисто квантовым эффектом. Этот результат непосредственно следует из неразличимости неортогональных квантовых состояний.
Пример 6 . Допустим, что задано начальное состояние р , тип передачи сообщения и соответствующее количество передаваемой информации. Возрастание корреляции можно охарактеризовать следующими функциями:
ICll max ICl l (одностороннее классическое сообщение) ;
l
ICll max ICll (двухстороннее классическое сообщение) .
Оператор к – операция над двухчастичным состоянием, которая состоит из локальных операций и содержит не более чем 2l классических или l квантовых битов в сообщении. Это отражено в соответствующих верхних индексах l или l. Через ри р’ обозначены состояния до и после проведения операций с обменом сообщениями, p' = ^ р . Количество корреляции I l р , скрытой (ненаблюдаемой) в состоянии с l квантовыми битами при одностороннем обмене сообщениями, может быть ограничено следующим условием: I l р -I р ICll р - ICl р 2l + O d2ICl р logICl р. Скрытая (наблюдаемая) классическая корреляция в квантовом состоянии. Обсудим ситуацию, в которой некоторое количество корреляции не доступно наблюдению при одностороннем обмене сообщениями. Начальное состояние определяется подсистемами A и B на соответствующих подпространствах размерностью 2d и d в виде: d11 р=1d11 k)(k|®|t)(tIA® Utk k Ut† , (11) 2d k0t0 где операторы U I и U меняют исходный вычислительный базис на объединённый как i U1 Ik 1 i, k . Тогда B выбирает случайным образом состояние Ik из d состояний в двух возможных рандомизированных базисах (в зависимости от случая, когда t 0 или 1 в (11)). В то же время наблюдатель A имеет полную информацию о квантовом состоянии наблюдателя B . Получив необходимое количество информации в виде Il logd+ 1 , A посылает значение t к B , который в свою очередь применяет оператор U к своему состоянию и измеряет значение k в вычислительном базисе. В результате A и B имеют измерение k и t , что даёт Il logd+ 1 бит корреляции. Состояние р эволюционирует по следующему сценарию. Пусть d 2n . Тогда A выбирает случайным образом k длиной в n битов и посылает к B сообщение о состоянии Ik^ или Hnk в зависимости от случайного значения бита t 0 или 1. Здесь H – преобразование Адамара; A посылает t кВ и позже наблюдает созданную корреляцию. Экспериментально установлено, что применения преобразования Адамара и измерения состояния квантовых битов достаточно, чтобы реализовать процедуру приготовления состояния и затем извлечь скрытую в состоянии классическую корреляцию. Начальная корреляция является малой величиной, Il logd. После полного измерения МА при одностороннем обмене сообщениями конечное значение количества информации в квантовом состоянии определяется как I I l logd 1 , т.е. количество доступной информации увеличивается. Примечание 2. Отметим, что полное измерение МА в базисе |^)®|t) оптимально для системы A . Выходное значение результата измерения точно даёт информацию о том, какое чистое состояние из ансамбля выбрано. Поэтому имеется возможность применить классический, локальный процесс обработки (результата измерения) для получения информации о распределении результатов других измерений. Для системы A выбор оптимального измерения позволяет для системы В извлечь из Icl р доступное количество информации IAcc об ансамбле равномерно распределённых состояний k , U1 H k • k0, , d1 - Доступная информация об ансамбле смешанных состояний. В общем случае доступная информация об ансамбле смешанных состояний E p , определяется как максимальная взаимная информация между измеряемым состоянием с индексом i и результатом его измерения. Количество доступной информации I E можно охарактеризовать как максимальное значение информации, извлекаемое из квантового состояния с помощью ПООЗ-измерений (разд. 2) с элементами только ранга 1. Допустим, что M= а^ф/}(^| означает ПООЗ-измерение с элементами ранга 1, где каждое состояние |^0 нормализовано и а/> 0. Тогда IAcс E можно вычислить как: IAcc E max M pi log pi pi j j i j log i ii Классическая часть , Квантовая часть где ц = ^ p^t . Применим теперь выражение (12) к решению вышеупомянутой проблемы. Ансамбль состояний задается как при k, t следующих значениях 1I i k,t; pk,t , и 2d2 IAcc E , получим: . Подставляя все из приведенных выражений в формулу для ICl E max M log2d j jUtk2log jUt Классическая часть j ,k ,t Квантовая часть max M logd j 1 j Ut k2log j Ut k2 Классическая часть j k , t Квантовая часть где использованы следующие обозначения: j d и k 1 . Так как выполняется j j соотношение 1 то второе выражение является выпуклой комбинацией и может быть ограни- jd чено сверху путём операции максимизации по первому члену в виде ICl E logd max 1 Ut k2log Ut k2. k, t Отметим, что член представляет сумму энтропийных мер k, t измеряемого состояния в вычислительном и в обобщённом базисах. Такая сумма энтропий ограничена величиной logd . Нижние границы подобного типа в теории квантовых измерений называются неравенствами энтропийной неопределённости (EUI), которые количественно определяют невозможность одновременного извлечения вектора из двух обобщённых (совместных) базисов. Из приведенных соотношений следует, что Ilog d. Равенство можно достигнуть, если B измеряется в вычислительном базисе I ci P=1log d - IC P - I a P=1 + 1log d . Отметим, что свойство приращения пропорциональности выполняется для многократных копий состояния . Wootters показал, что доступная информация из m независимых копий ансамбля E разделённых состояний аддитивна, I Em mI E. Отсюда следует, что для рассматриваемого случая имеем: I m mI . Пример 7. Пусть задано двухчастичное состояние . Определим возможную меру классической корреляции между подсистемами A и B как: CorB AB max S A B piS Ai i , где Tr – редуцированная матрица плотности. Энтропия фон Неймана S Tr log . Условная матрица плотности Ai определяется через матрицы плотности состояния A после реализации измерения B над состоянием B в виде: Ai TrB Bi AB TrAB Bi AB . Вероятность определить A в состоянии Ai есть p Tr B . Мера корреляции (13) имеет простую физическую интерпретацию: если A и B не коррелированны, то маргинальное значение энтропии S A состояния A и взвешенное усреднённое значение энтропии A после ПООЗ- измерения pS i над состоянием B дает как следствие Cor 0, так как для i некоррелированной системы AB состояние A не состоянием B . Более того, отметим, что имеет место зависит от действия ПООЗ- измерения над соотношение A pi Ai ; тогда для данного i ПООЗ-измерения над системой B выражение S A piS Ai i задает дефект энтропии. Следовательно, классическую корреляцию Cor можно рассматривать как максимальное осреднённое возрастание энтропии системы A , когда состояние Ai (после завершения измерения B над системой B ) является специфически сравнимым с ситуацией, в которой известны только смешанные состояния . Классическая корреляция устанавливает меру силы корреляции двух подсистем без указания приоритета подсистемы, используемой для извлечения данной корреляции. Количество квантовой взаимной информации I A: B двухчастичной составной системы AB можно декомпозировать на дефицит информации (или работы) и дефицит классической информации в виде I . Это приводит к естественной аналогии с процессом декомпозиции для случая количества взаимной информации, используемой при описании различных мер классической корреляции. Количество оцененной классической корреляции и относительной энтропии E в запутанных состояниях также не превышает в сумме количества взаимной информации фон Неймана между двумя подсистемами, т.е. I р*.в >[С рдв "pt^EREn.,,. Физически это означает, что выбор неоптимального ПООЗ-измерения может разрушить полную корреляцию. Естественно, что при рассмотрении всех возможных ПООЗ-измерений для данного состояния оптимальный класс ПООЗ-измерений не может устранить полную корреляцию. Другой альтернативой, которая делает совместимыми понятия классической корреляции и взаимной информации, является возможность различных определений мер квантовых корреляций, отличных от представления последних в виде E . Одним из возможных кандидатов служит квантовый беспорядок. Пример 8: Взаимная информация и квантовый беспорядок. В противоположность к определению классической условной энтропии квантовая условная энтропия является зависимой величиной от процедуры измерения, проводимой над исследуемой системой. Мерой квантового беспорядка выступает: 5 A: B -I A: B - J A: B в . i Величина J задает информацию о системе B по результатам серии измерений B J A: B =S A -S a| ПВ =S A -^Pi5 * Pt , где pi и iA изначально выбраны как специальные случаи p и iA , когда множества измерений формируются как ограниченные одномерные проекции iB . Приведенное определение квантового беспорядка четко описывает неразделимую зависимость квантовой условной энтропии от процедуры измерения3. Мера квантового беспорядка равна нулю, если существует такое (хотя бы одно) измерение, для которого эта мера принимает нулевое значение. Поэтому минимальному значению меры квантового беспорядка сопоставляют квантовую корреляцию. При выборе соответствующего множества измерений над системой B , определённого как множество одномерных проекций, нетрудно проверить, что множество измерений, при которых минимизируется квантовый беспорядок, т.е. максимизируется величина J , эквивалентно ПООЗ -измерениям, оптимизирующим меру классических корреляций бинарных состояний. Данный результат следует из определения этих количественных мер и результата оптимизации классических корреляций при использовании только проективных измерений. Следовательно, имеем max J A: B nB c(^orB pAB . Поэтому, I A: B cC2orB +min(? A: B , т.е. для бинарных состояний i iB классическая корреляция и квантовый беспорядок выступают составными компонентами в оценке взаимной информации. Поэтому не существует измерения, извлекающего классическую корреляцию и способного изменить значение взаимной информации между двумя подсистемами при добавлении классической корреляции к относительной энтропии. Это подтверждает утверждение, что удобнее Электронный журнал «Системный анализ в науке и образовании» Выпуск №4, 2013 год использовать понятие квантового беспорядка в качестве квантовой составной части для классической корреляции вместо относительной энтропии. Моделирование квантовых алгоритмических ячеек и квантовое программирование В настоящее время разработка теории и практики «квантовой информатики» в целом интенсивно развивается по всем направлениям, включая создание языков и систем квантового программирования. В настоящей статье приведены лишь примеры первоначальных сведений о средствах, применяемых в этой последней области. Для серьезного овладения квантовым программированием читатель может обратиться к библиографическим ссылкам [28-34] и мн. др. Основу метода проектирования квантовых алгоритмических схем и ему подобных методов формирования новых типов КА составляет система проектирования квантовых алгоритмических ячеек (КАЯ). Как и в общей структуре КА, структура системы проектирования КАЯ основана на формализации описания трёх основных квантовых операторов (суперпозиции, квантовой корреляции (запутанных состояний) и интерференции) и измерения в виде элементарных эволюционных унитарных операторов. В соответствии с квантовой схемой КА данные операторы собраны тензорным и прямым произведением в единый эволюционный квантовый унитарный оператор. Система моделирования квантовых вычислений и КА реализуется на классических компьютерах с применением КАЯ. Процесс проектирования КАЯ в матричной форме заключается в проектировании трех квантовых операторов: суперпозиции (Sup), квантовой корреляции (запутанных состояний – entanglement U ), и интерференции (Int) и составляют основу структур КА. В общем виде структура КАЯ может быть представлена в виде: КАЯ Int ®nI Uh1 nH ®mS] , (14) где I – оператор идентичности; ® – символ тензорного произведения; S равен I или матрице Адамара и выбор зависит от описания исследуемых свойств функции. Одной из особенностей процесса проектирования (1) является выбор типа оператора U , физически описывающего тип квантовой корреляции и закодированные в суперпозиции качественные свойства исследуемой функции f . Работа квантовых операторов осуществляется в итеративном режиме в зависимости от типа КА. При этом для общего случая предполагается, что определённые вычислительные проблемы могут быть решены на квантовом компьютере более эффективно (с меньшей вычислительной сложностью, так называемая NP – проблема), чем на классическом компьютере. Более того, с помощью эффективного применения квантового компьютера достигаются решения алгоритмически неразрешимых (на классическом уровне) проблем. Таким образом, существуют эффективно решаемые с помощью применения КА задачи, для которых не существует ни одного успешного классического (рандомизированного) алгоритма. Эти наблюдения свидетельствуют о том, что КА составляют физически обоснованный базис не только техники ускорения вычислений, но и поиска решений сложных проблем, используя такие квантовые законы, как суперпозиция (для расширения пространства возможных решений), квантовый параллелизм процессов вычислений (в интересах ускорения поиска решений) и квантовая интерференция (с целью извлечения искомого решения). Структурно КАЯ действует на начальный канонический базисный вектор и формирует комплексную линейную комбинацию состояний составляющих классических векторов (называемую суперпозицией) в виде базисных векторов как выходной результат действия оператора суперпозиции. Суперпозиция содержит в качестве одной из составляющих информацию о решении исследуемой проблемы. После процесса формирования суперпозиции в КАЯ применяются операторы квантовой корреляции, интерференции и измерения с целью извлечения информации об искомом решении. В квантовой механике процесс измерения носит необратимый характер и является недетерминированной операцией, что приводит к измерению только одного из базисных векторов в сформированной суперпозиции. Вероятность каждого базисного вектора быть результатом измерения в составе суперпозиции при заданном вычислительном базисе зависит от комплексного коэффициента (амплитуды вероятности). Процесс останова итерационного действия КАЯ осуществляется программным путем на основе принципа минимума информационной энтропии «интеллектуального квантового состояния», содержащего ценную информацию об искомом решении. КАЯ могут быть реализованы с помощью программно-аппаратной поддержки эволюционных квантовых вычислений. Квантовое программирование В квантовом программировании существует доказательство полноты описания КАЯ с помощью соответствующих программных языков повышенной семантической выразительности. По аналогии с существованием эквивалентности в теории вычислений, которая основана на классических алгоритмах, известна гипотеза об эквивалентности между представлением выражений квантовых операций на синтаксическом уровне с сохранением полноты их описания за счет включения в квантовые языки программирования семантической выразительности квантовых операторов (на функциональном уровне описания действий квантовых операторов). Одним из естественных шагов в этом направлении является разработка принципов логического вывода и проверки истинности суждений в языках квантового программирования для устранения противоречий в получаемом следствии логического вывода. К таким языкам квантового программирования следует отнести, например язык QPL (Quantum Programming Language) и др. Рассмотрим, как осуществляется в языке QPL непротиворечивое описание, например, определения действия оператора Адамара в следующем виде: H x if x then false + -1* true else false + true . Оценим полноту и истинность данного выражения, которое эквивалентно проверке истинности того, что последовательное действие операторов Адамара H H x на функциональном уровне описания приводит к результату, эквивалентному x . Для этого используем следующую модель логического вывода языка QPL: H H x if if x then false + —1 true else false + true then false + —1 * true else false + true by commuting conversion for "if" = if x then if false + ^ 1 true then false + ^ 1 true else false + true else if false + true then false + ^ 1 true else false + true by "if" = if x then false false + true + true else false + false + true true by simplification and normalisation = if x then true else false by л -rule for "if" = x Элементы теории проверки полноты и истинности семантики функционального описания КА на языке функционального квантового программирования QPL описаны ниже. – Квантовые языки программирования. При проектировании языка программирования одна из целей состоит в том, чтобы идентифицировать и проработать полезные понятия "высокого уровня" — абстракции или парадигмы, которые позволяют решать проблему концептуальным способом, вместо сосредоточения на деталях его выполнения. Исследование квантовых языков программирования обеспечивает урегулирование, в котором можно исследовать возможные языковые особенности и проверять их полноту и экспрессивность. Кроме того, определение прототипа языков программирования создает объединяющую формальную структуру, для рассмотрения и анализа существующего квантового алгоритма. – Модели виртуальных машин. Развитие языков программирования часто вызывается наряду с другими причинами развитием методов проектирования компиляторов. В случае квантовых вычислений ситуация усложняется отсутствием (в настоящее время) пригодной к использованию квантовой вычислительной аппаратуры. Чтобы иметь возможность говорит о «реализации», необходимо определить некоторую «виртуальную» модель вычислительной машины и работать с ней. При этом следует понимать, что будущая реальная квантовая машина, возможно, будет существенно отличаться от этой виртуальной модели, но эти отличия в идеальном случае должны быть прозрачными для программиста и обрабатываться автоматически компилятором или операционной системой. Существуют несколько возможных моделей виртуальных машин, но все они эквивалентны, по крайней мере, теоретически. Таким образом, можно подобрать модель, которая наилучшим образом соответствует вычислительной интуиции. По-видимому, наиболее популярной и понятной виртуальной моделью машины является модель квантовой цепи. Квантовая цепь строится из квантовых ячеек точно таким же образом, как классическая логическая цепь – из логических ячеек. Отличие состоит в том, что квантовые ячейки всегда обратимы и соответствуют унитарным преобразованиям в пространстве комплексных векторов. Модель квантовой схеме в основном рассматривает унитарные преобразования как основные базовые операции. Другой базовой операцией является измерение, которое выполняется как последний шаг в процессе вычисления. Другая модель виртуальной машины, возможно даже более подходящая для интерпретации квантовых языков программирования, – модель QRAM, предложенная Knill. В этой модели допускается свободное перемешивание унитарных преобразований и измерений. Квантовым устройством управляет универсальный классический компьютер. Это квантовое устройство содержит большое, но конечное число индивидуально адресуемых кубитов точно такое, как в классическом чипе памяти содержится конечное множество классических битов. Классический контроллер посылает последовательность инструкций («команд»), каждая из которых имеет вид «применить унитарное преобразование U к кубитам i и j» или «измерить кубит j». Квантовое устройство выполняет эти инструкции и выдает в качестве ответа результаты доступных измерений. Иногда в работах по теории сложности используется третья модель виртуальной машины – квантовая машина Тьюринга. В этой модели измерение не производится, а все операции предполагаются унитарными. Машина сдержит ленту, головку и конечный набор управляющих правил перехода, аналогично классическому варианту. Хотя теоретически эта модель эквивалентна двум предыдущим, в общем случае она не рассматривается как достаточно реалистическое приближение для возможных будущих квантовых компьютеров. – Императивные квантовые языки программирования. Ранее предложенные квантовые языки программирования следовали за императивной программной парадигмой. Эта линия языков была начата Knill, который определил ряд соглашений для выражения квантовых алгоритмов в псевдокоде. Несмотря на то, что предложение Knill было не очень формально, оно оказало большое влияние при проектировании более поздних императивных квантовых языков программирования. Более полные императивные языки были определены Omer, Sanders и Zuliani, Bettelli и мн. др. Общая черта этих императивных квантовых языков программирования заключается в том, что программа рассматривается как последовательность операций, которые работают, обновляя некоторое глобальное состояние. Эти языки могут быть непосредственно скомпилированы или интерпретироваться в реальную модель аппаратных средств QRAM. Квантовые состояния в этой парадигме, как правило, реализованы как массивы кубитов, и во время выполнения необходимы средства обнаружения ошибочных условий. Кроме того, обычно эти языки не имеют формальной семантики, за исключением языка Sanders и Zuliani, который обладает операционной семантикой. Различные языки в этой категории предлагают множество программных особенностей. Например, QCL содержит такие функции, как, автоматическое управление рабочей памятью, и богатый язык для описания пользовательских операторов. Предложено несколько операций более высокого порядка, таких как вычисление инверсии определенного пользователем оператора. Язык Bettelli и мн. др. уделяют особое внимание практичности применения. Языки задуманы, как расширение C++, и рассматриваются как квантовые операторы объектов первого порядка, которые могут быть явно построены и управляться во время выполнения. Одна из самых серьезных особенностей этого языка - непрерывная оптимизация квантовых операторов, которая производится во времени выполнении. – Функциональные квантовые языки программирования. В функциональном программировании, программы работают не на обновлении глобального состояния, а на отображении конкретных входов на выходы. Типы данных, связанные с чисто функциональными языками, (такие как списки, рекурсивные типы), более поддаются анализу во время компиляции, чем их императивные аналоги (такие как массивы). Следовательно, даже в очень простых функциональных языках программирования можно избежать многих проверок во время исполнения. В первом предложении варианта функционального квантового языка программирования введен язык QFC, который представляет программы через функциональную версию блок - схем. У языка также есть альтернативный синтаксис, основанный на текстовом представлении. И унитарные операции и измерения непосредственно встроены в язык, и обрабатываются с сохранением типов. Классические и квантовые особенности интегрированы в рамках одного формализма. Отсутствует контроль соответствия типов во время выполнения или обработки ошибок. Язык может быть откомпилирован на модель QRAM, а также обладает полной денотационной семантикой, которая может использоваться для формальных рассуждений о программах. Основной квантовый язык блок-схем функционален, поскольку свободен от побочных эффектов. Однако, функции сами по себе не рассматриваются как данные, и, таким образом язык теряет черты более высокого порядка. Таблица 2. Классификация языков программирования Тип языка QCL Q language qGCL (Block-)QPL императивный язык + + + функциональный язык + прагматический подход + + теоретический подход + + формальная семантика + + универсальный язык + + + + Пример. Рассмотрим некоторые свойства языков квантового программирования. QCL (Quantum Computation Language) Общие свойства фактически первый квантовый язык программирования (элементарный) процедурный язык автоматическое управление рабочим пространством синтаксическая обратимость определяемых пользователем квантовых операций синтаксис как в C / Паскаль универсальный язык: может осуществить и моделировать все известные квантовые алгоритмы отсутствует формальная семантика нетривиальные унитарные операции – функции (функциональный синтаксис запроса). Далее приведен пример «Вычисление факториала» на языке QCL с помощью классического программирования: // program example: recursive // and non-recursive function call: int factorialR(int x) { // recursive implementation // precondition x >= 0 if x == 0 { return 1; } return x*factorialR(x-1); } int x = 5; print x, "! = ", factorialR(x); //--------------------------------- int factorialNR(int x) { // iterative implementation // precondition x >= 0 int k; int y = x; if (y == 0) or (y == 1) { return 1; } else { // "else" for better readability // here: y >= 2 k = y; while y >= 3 { y = y - 1; k = k*y; } return k; } } x = 7; print x, "! = ", factorialNR(x); print "The End."; /* result: : 5 ! = 120 : 7 ! = 5040 : The End. */ Квантовые операторы и их действие 1. Оператор тождественности Qopmy_op 2. Встроенные квантовые операторы Qopmy_op = QHadamard (7) 3. Квантовые операторы Qopmyop = QFourier (7) 4. Переупорядочение строки Qubit, Qopa_swap = QSwap (5) 5. Операторы управления Qopa_controlled_op (U, 5) 6. Операторы для классических функций Qopan_oracle = Qop (f, 3, 5) 7. Оформление структуры оператора Qopcomposed = part_1 &part_2 8. Оператор связи Qopadj_operator =! an_op 9. Оператор перестановки Qopsplit = an_op(2, 3, SPLIT) 10. Применение оператора an_operator (a_register) qGCL (Quantum Guarded Command Language) Общие свойства qGCL: выражается через pGCL (вероятностный командный язык) qGCL: императивный язык подходит в качестве языка спецификаций (высокий уровень математической нотации) механизм пошагового уточнения программы для вывода и проверки (доказательство корректности) формальная семантика: пред – и пост-условия распространяются на пред- и пост-ожидания включает в себя три квантовых примитива на высоком уровне: состояние подготовки, эволюции, наблюдения универсальный язык. – Блок-схема QPL (Квантовая блок-схема). Квантовая блок-схема практически не отличается от классической, только в квантовой блок-схеме добавляется новый тип переменной, названный qbit, а также возникают новые операции: унитарные преобразования и измерения (см. рис. 1 а,б). (а) (б) Рис. 1. Квантовая блок-схема - Правила для квантовых блок-схем При составлении квантовых блок-схем используются некоторые правила, представленные на рис. 2: выделение бита (Allocatebit), отменить бит (Discardbit), унитарное преобразование (Unitary transformation), cлияние (Merge), перестановка (Permutation), измерение (Measurement), перестановка (Permutation). Рис. 2. Правила преобразований в квантовых блок-схемах – Примеры Первый пример показывает правильность преобразования программы: измерение, сопровождаемое перемещением. Правильность этого преобразования в программе состоит в том, что операция «отбрасывания» уже встраивает неявное измерение в программу. Во втором примере следующие две схемы являются взаимно обратными: В третьем примере представлена схема квантового преобразования Фурье: Z:qbit [disc^dn] h, a?:qbit, у: qbit list, n:int mZ:I A:qbit, nit: I U^Mnaj] (=132(1,9)"] A:qbitJ:qbitlist :qbit,i:qbit list 11 = ini(w/jj 11 = ing (h-., tj~| Z:qbit list :qbit list list j output Z:qbit list ] OFT:pnput Z:qbit list J I Z:qbit list rotate: J^input Л :дЬЛ, t:qbit list, n:intj I A:qbit. t:qbit list, n:int Ш1 nil A:qbit,mf:I,n:int / caseT> i \ 6:qbit 8 qbit list |(MW A:qbit, t:qbit list Atqbit, t:qbit list I new mt n := 2 | I (A, y) = rotate (A., y, raj | h,z:qbit,9:qbitBst A:qbit, t:qbit list,n:int j (A.t) = rotatel/i, t.tijj] /i:qbit, t:qbit list |№)| /i:qbit, t:qbit list |/i:qbit, t:qbit list [ output /i:qbit,t:qbitlis?] case f> j^v\ Ш2с h, Ttqbit, y:qbit list, nint x^h* = R«\ Пример 9: Квантовое лямбда-исчисление. Рассмотрим основные определения и понятия данного вида квантового программирования (см. Приложение). – Термы. Язык использует обозначения интуиционистского лямбда-исчисления4. Рассматриваются обозначения стандартного лямбда-исчисления с булевыми и конечными переменными. Расширение стандартного языка осуществляется за счет введения трех специальных квантовых операций типа new, meas, built-in unitary gates (встраиваемые унитарные ячейки). Операция new отображает классический бит в квантовый бит; meas отображает квантовый бит в классический бит посредством операции измерения и является вероятностной операцией. Предполагается, что существует множество U n встраиваемых (built-in) унитарных ячеек для каждого n . Через U обозначим область всех множеств Un . Тогда синтаксис языка можно представить в виде: Term M , N, P :: xI MN|Яx.M | if M then N else P 0 1 meas | new | U |*|(M,N)|let x, y ) = M in N. Термы идентифицируются с точностью до a – эквивалентности и используется упрощенная запись типа (M1, , Mn ) = (M1,(M2, . – Программы. Введение в язык синтаксиса постоянных квантовых состояний, таких как a|01} в виде лямбда терма типа X x. a| 0) + p\ 1 в общем случае не эффективно. Рассмотрим, например, лямбда терм Xy.f.fpy q , где p и q запутанные квантовые биты в состоянии | pq) = al 00)+/?|11} . Такое состояние невозможно представить локально в виде произведения отдельных множителей p и q с постоянными множителями. Нелокальная природа квантовых состояний требует уровня косвенного введения представления состояния квантовых программ. Определение 1. Состояние программы представляется триплетом Q,L,M , где Q – нормализованный вектор ®in01C 2 для некоторого n 0 ; M – лямбда терм; L – функция отображения из W в 0, , n 1 , где FV MczWcz Vterm . L называют также связывающей функцией или кубит события. Назначением данной функции является установление соответствия между свободными переменными в M с соответствующими кубитами в Q . Введение условия a -эквивалентности распространяется естественным образом на программы, например, состояния [| 1 } ,x 0,X y. x]и [| 1 ,z 0,X y .x] эквивалентны. Множество состояний a -эквивалентных программ обозначается через S . В дальнейшем, с целью упрощения обозначений, через p будем обозначать свободную переменную x так что выполняется соотношение L x i . Программа Q,L,M обозначается как Q,M и M M[pin/x1 pin/xn]где ikL xk. – Операционная семантика. Определим вероятностные процедуры редукции значений вызываемых переменных для квантового лямбда исчисления. Отметим, сама процедура также носит вероятностный характер, а выбор значений на каждом шаге редукции носит детерминированный характер. Определение: Значение (value) является термом следующей формы: Value V,M :: xг x.M 0 1 I meas I new I U1*1^V,M ). Множество состояний значений обозначается как VQ,V,L S I VG Value . Правила редукции перечислены в Табл. 3, где использованы принятые ранее соглашения об обозначениях. Таблица 3. Правила редукции квантового лямбда исчисления [^(Az-M^l^ilQ.MM [Л] ^[QW] [Q, if 0 then M else W] —>1 [Q, TV] [Q, if 1 then M else TV] —>1 [Q, M] [<9, ^(Pji,- ■ • ,Pj„)l — 1 IQ', (Pii,-• • ,Pf„)] \Q,MN^ ^p [Q',MN'] [Q,M] ^p ^.Ml [Q.MV] — p[Q',MV] [a Qo) + /?|Qi),meos pt] —>|a|2 [|(?o),O] [Q,M1] ^p [g;^] [a|Qo} +^|Qi),meas pj] —^ [|Qi},l] [Q,(M1,M2)] -^р^^'.Мз)] [Q, new 0] —>1 [Q 0 |0),p„] -j^j-^pj^L- [Q, new 1]—>1 [Q®|l),pn] [Q,(Vi,M2)]^p[Q',(Vi,M^] __ [Q, if P then M else TV] —>p [Q', if P' then M else TV] _______[ОЖ^ИОЖ]_______ [Q,let (ti,T2) = TVf inTV] —^p [Q\let (xi,X2) = M' in TV] [QJet (тьх2) = (Vb V2) m TV] Ю№/хъУ2М Конечное отношение определяется как ∽ , которое моделирует преобразования в присутствии декогеренции или неточности физических операций. Тогда Q,M ∽ Q ,M определяет Q,M p Q,M даже когда p 0, плюс дополнительная операция, если Q и Q являются векторами одинаковой размерности: Q,M ∽ Q ,M . Пример 10: Эксперимент Белла. Два квантовых бита А и В образуют максимальное запутанное состояние AB1 = I0)®l1 1 0) . Эти кубиты V2 посылаются Алисе и Бобу, соответственно. Допустим, что Алиса и Боб могут независимо друг от друга выбрать один из трех базисов a,b,c для измерения своего кубита: 1 0a ■40),1 0b1■1 0)+ 3■11,1 0c1 10V 31, 1 0a -\0),1 0b1■1 0)+ 3■11, 1 0c 1 10)- 31, >11, I 1b 3■I0)- 1I1, I 1c 3■I0Л1I1) Требуется вычислить вероятность получения одинакового выходного результата в случае измерения А и В относительно каждого из девяти возможных выборов пары базисов. Можно интерпретировать данный эксперимент в контексте квантовых вычислений высокого уровня. Во-первых, приготовление состояния может рассматриваться как отображение EPR: • qbit ® qbit . Тогда Алиса и Боб принимают свой кубит, выбирают базис, и проводит измерение: осуществляется применением функции f : qbit ® trit bit , где элемент trit 0,1,2 является классическим триплетом. Тогда данную функцию можно представить в виде f : qbit trit bit . Эксперимент Белла можно рассматривать как композицию: EPR qbit ®qbit ff—> trit bit ® trit bit , которая воспроизводит терм типа trit bit 0 trit bit , т.е., пару ( f,g функций запутанных состояний. Данный тип результата является по своей физической природе чисто классическим; неравенство Белла доказывает, что не существует классической вероятностной пары функций, проявляющих подобное поведение, т.е. таких что f x g x с вероятностью 1 при xy, но с вероятностью ¼ при xy. Рассмотрим возможность применения квантовой логики для анализа квантовых программ. Квантовая логика для анализа квантовых программ. Формализм представления подпространств в терминах языка пропозиционального исчисления включает два элемента: язык (т.е., пропозициональные термы) L и функцию интерпретации , которая отображает каждый терм языка в замкнутое подпространство гильбертова H . В этом случае, каждый терм p е L ассоциируется с замкнутым подпространством H , обозначаемое как p . Язык L содержит две связки: отрицание —। и конъюнкцию л , а также множество констант Т . Таким образом, каждая константа p G^ является термом (т.е., p е L ) и задаются два терма p,q еL и оба p и pq являются также термами. Определение функции интерпретации основано на структуре термов и соответствии между отрицанием —। и ортодополнением ± с одной стороны, и между конъюнкцией и пересечением пс другой стороны. Тогда определение можно задать как: v pЕ L, p p , p,q L, pqpп q . (15) Определение (15) полно при интерпретации каждого атомарного высказывания. Рассмотрим частный случай, когда пространство Гильберта H имеет вид 0n C 2 и имеем атомарные высказывания z и x 1 in. На интуитивном уровне высказываниям можно сопоставить соответствующее направление i -го кубита. Если n 1 , то интерпретации можно определить с помощью выражения zC 1 xCI-) = C I 0) -|1 } , и для n 1 данное определение расширяется до применения тензорных произведений. Например, x = ®i1C2 C n1C2 . (16) Тогда к двум константам применимо обычные определения: истинность высказывания T проверяется непосредственно (их интерпретация T эквивалентна полному пространству Гильберта H ) и абсурдное высказывание ± , истинность которого невозможно проверить так, что ± = 0. Пример 11: Описание ЭПР пары. Данное логическое состояние содержит описание многих интересных состояний квантовой системы. Для иллюстрации данного свойства рассмотрим высказывание z z л x x , которое полностью описывает ЭПР пару: zz zzлzz z1 © z пz ©z CI 00)фC| 10)®C | 11} ®C| 00)®C| 01}фC | 11) =C| 00)+C | 11). x1x2CC|--) , | zz xx8=zzпxx C I 00)® C I 11) Г1 C1++)®C C00 CI11 Эквивалентным образом можно использовать выражение z ©z <^± л x© 2 x2 для описания ЭПР пары. В этом случае © интерпретируется как сложение по модулю 2, связка означает эквивалентность и ± есть 0. Аналогично можно показать, что выражение z©z 4^± Л z©z <^± л x© 2 x2 © x полностью описывает запутанное GHZ состояние. Пример 12: Порождение ЭПР пары. Традиционно Процесс генерации ЭПР пары стартует из состояния I 00 (которое описывается логическим соотношением zz или эквивалентным выражением zzо± ) применением оператора Адамара H и затем ® 1,2 к системе, представленной на схеме рис. 3. Рис. 3. Схема порождения ЭПР пары Логически квантовая схема выполняет следующую последовательность операций: Hzл—1z2 ”ђ H1 z H z ”ђ H1 z1 H1 z2 ”ђ x1z2 1,2 ] H1 z1 z2 ” ђ [ф1,2 ] -x1 z2 ”ђ - [©1,2 ] x1 Л^ [©1,2 ] z2 ”ђ x ®x л—1 zф 2z2 ” ђ x1x zz Как и ожидалось, конечное высказывание x x А z z полностью характеризует подпространство, натянутое ЭПР парами, что соответствует результатам предыдущего примера. Программное обеспечение эмулятора квантового алгоритма Рассмотрим кратко вопросы моделирования квантовых вычислений и квантовых алгоритмов на классических компьютерах с архитектурой фон Неймана. Структура системы моделирования квантового алгоритма На рис. 4 показана структура программного обеспечения системы моделирования квантового алгоритма (КА). Программное обеспечение (ПО) системы разделено на две части. Первая часть включает в себя общие функции. Во вторую часть входят специализированные алгоритмические функции, реализующие конкретные алгоритмы. Перечислим общие функции: Блок выбора суперпозиции; Операторы интерференции; Бра-Кэт функции; Операторы измерения; Операторы вычисления энтропии; Функции визуализации; Функции визуализации состояния; Оператор визуализации. Специализированные алгоритмические функции включают в себя: Декодирование запутанных состояний (квантовая корреляция); Проблемный преобразователь; Интерпретатор результатов; Сценарии выполнения алгоритмов; Сценарий выполнения алгоритма Дойча; Сценарий выполнения алгоритма Дойча-Джоза; Сценарий выполнения алгоритма Гровера; Сценарий выполнения алгоритма Шора; Сценарий квантового алгоритма управления алгоритмами. Функции визуализации – это функции, которые обеспечивают корректное отображение амплитуд вектора квантового состояния, а также визуализация структуры квантовых операторов. Специализированные алгоритмические функции обеспечивают набор сценариев для выполнения КА в общей части и инструментарий для моделирования КА, включая и КА управления алгоритмами. Функции второй части подготавливают операторы для каждого из указанных алгоритмов, используя операнды из первой общей части. Команды, используемые в КА. Пример выполнения алгоритма Гровера представлен на рис. 5-11. В частности, на рис. 5 показан алгоритм подготовки операторов суперпозиции, квантовой корреляции и интерференции для алгоритма Гровера с тремя кубитами (включая процедуру измерения кубита). Затем операторы собираются в квантовую ячейку. В приведенном примере на рис. 5 показан запуск сценария с начальным состоянием |in> = |001> и вычисление конечного состояния |out> = G|in>. В процессе выполнения данного сценария в программе Matlab осуществляется выделение памяти для оператора матриц и векторов состояния. Полученные квантовые операторы матриц представлен на рис. 7. Вектора начального и выходного состояний, а также квантовая ячейка показаны на рис. 8. Для демонстрации результатов, код функций визуализации представлен на рис. 6. На основе этих данных была построена 3D-визуализация оператора матриц (рис. 9). Здесь вертикальная ось показывает амплитуду соответствующих элементов матриц. Индексы элементов проставлены согласно нотации кэт. Визуализация квантовых состояний, начального и выходного, продемонстрирована на рис. 11. На рис. 11 вертикальная ось соответствует вероятности амплитуд компонент вектора состояния, а горизонтальная ось соответствует индексу компоненты вектора состояния, согласно нотации кэт. Другой подобный КА может быть сформулирован и выполнен с использованием аналогичных сценариев, и с помощью соответствующих уравнений, взятых из предыдущей части. Общие функции Блок выбора суперпозиции Алгоритмические функции Система моделирования квантовых алгоритмов Квантовая корреляция нифицированные операторы Операторы интерференции «Диффузия» -г Сценарии работы алгоритмов Интерпретатор результата Бра-Кэт функции Matlab демо Проблемный преобразователь Операторы измерения Deutsch’ KA Вычисление энтропии Консоль программ Matlab Функции визуализации Процесс проектирования КНВ и КА управления КА принятия решения Типовые функции ч Визуализация состояния Оператор визуализации Приложения Deutsch - Jozsa Поисковые КА Рис. 4. Структура программного обеспечения системы моделирования КА Рис. 5. Пример сценария моделирования алгоритма Гровера (код алгоритма) % Plot, results of calculations figure(1i subplot(221) plotoperators(SP); title('SP') Splot superposition operator subplot(222) plotoperators(ENT); title('ENT1) Splot entanglement operator subplot(223) plotoperators(INT); title('INT') Splot interference operator subplot(224) plotoperators(G); title(1G=INT*ENT*SP1)%plot operator figure(2) subplot(211) plotsuperposition(in); Splot input superposition title([1 IN,entropy_{SH}=1 num2str(entropySH(in)) , 1 entropy_{VN}=1 num2str(entropyVN(in*in1))]) subplot(212) plotsuperposition(out); %plot output superposition title([1 OUT, entropy_{SH} =1 num2str(entropySH(out)) , 1 entropy_{VN}=1 num2str(entropyVN(out*out1))]) Рис. 6. Пример сценария моделирования алгоритма Гровера (визуализация результата вычислений, выполнения команд) Рис. 7. Пример сценария моделирования алгоритма Гровера (операторы суперпозиции, квантовой корреляции и интерференции) Рис. 8. Пример сценария моделирования алгоритма Гровера (квантовый вентиль, входной вектор и результат выполнения квантового вентиля) Рис. 9. Пример сценария моделирования алгоритма Гровера (визуализация квантовых операторов) Рис. 10. Пример сценария моделирования алгоритма Гровера (визуализация квантовых состояний: входного и выходного) Г 1 V 0 ~ 0 ” о ” о * о ” о ~ о 1 1 1 1 1 1 4Ы№Н................. - 0 ' 6 О 11111111 Рис. 11. Диаграмма пакета Simulink моделирования произвольного КА Моделирование КА как динамической системы. Для того чтобы смоделировать поведение динамической системы, включающей в себя квантовые эффекты, нужно рассмотреть КА как динамическую систему в виде блок-схемы и затем имитировать его поведение во времени. На рис. 11 представлена диаграмма пакета Simulink программного продукта MatLab квантовой схемы расчетов верности квантового состояния и вычисления матрицы плотности |a> На рис. 11 показано, что входное значение разделяется на вычисление кэт-функции и бра-функции. Выходное значение кэт-функции является первым входным значением матрицы мультипликатора и вторым входным значением мультипликатора. Вычисленное выходное значение функции бра используется во втором входном значении матрицы мультипликатора, а также как первый вход в матрицу мультипликатора. Результатом работы мультипликатора является расчет матрицы плотности входного состояния, а также вероятность входного квантового состояния. Рис. 12. Диаграмма Simulink моделирования произвольного КА На рис. 12 показана Simulink-схема произвольного КА. Подобная схема может быть использована в моделировании ряда квантовых алгоритмов в среде Matlab/Simulink. Эмулятор квантового алгоритма Разработанное алгоритмическое представление КА может быть использовано для проектирования программного обеспечения (ПО) эмулятора КА. Ключевым моментом является уменьшение количества матричных операций вектора операций и последующая замена операций умножения. Это может привести к резкому увеличению производительности эмуляции, особенно в тех алгоритмах, которые не требуют комплексного числа операций, а также когда вектор квантового состояния имеет относительно простую структуру (например, такой как алгоритм поиска Гровера). Разработанное ПО было смоделировано для 4-х квантовых алгоритмов: Дойча-Джодза, Шора, Саймона и Гровера. Система использует единый интерфейс для всех алгоритмов, с вариантами 3D-визуализации динамики векторов квантового состояния и квантовых операторов. Стартовое окно приложения КА эмулятора представлено на рис. 13, в котором пользователь может выбрать создание новой модели КА или продолжить моделирование существующей. Рис. 13. Стартовое окно приложения КА эмулятора В случае создания новой модели КА следующим шагом будет выбор алгоритма (рис. 14). На данном этапе пользователь может выбрать не только алгоритм, но и задать нужную размерность. Система предусматривает работу с 50 и более кубитами, но из-за проблем визуализации рекомендуется ограничить число кубитов до 10-11. Рис. 14. Диалоговое окно режима создания модели КА приложения КА эмулятора После того, как были заданы начальные параметры в алгоритме, система отобразит первоначальный вектор состояния и выбранную структуру алгоритма в главном окне системы (рис. 15). Главное окно (рис. 15) содержит всю информацию о моделируемом квантовом алгоритме и реализует основные операции и осуществляет его анализ. В меню формы есть доступ к квантовым операторам (рис. 16), использовав их можно изменять входные функции (рис. 17). В системе предусмотрена возможность возврата: при нажатии на соответствующие стрелки можно сделать шаги вперед или назад по алгоритму; шаг, который применяется в настоящее время, будет выделен на схеме алгоритма. Меню эмулятора состоит из 4-х компонент: 1. Пункт File (Файл) обеспечивает основные операции, такие как загрузить/сохранить проект, создание новой модели. 2. Пункт Model (Модель) осуществляет доступ к изменению входных функций (рис. 17). 3. Пункт View (Вид) обеспечивает доступ к матричному оператору визуализаторов, включая операторы суперпозиции, квантовой корреляции и интерференции. Также есть возможность просмотра 3D-визуализации алгоритма динамики квантового состояния (рис. 18). 4. Пункт Help (Помощь) позволяет просмотреть документацию по приложению. Рис. 15. Главное окно приложения КА эмулятора (поисковый алгоритм Гровера, 3 кубита). Интерфейс с вкладками в нижней части окна позволяет просмотреть график энтропии Шеннона и 3D представление динамики вектора квантового состояния, а также в обычный, простой график квантового состояния. Размер вкладок может быть изменен путем перетаскивания разделителя между ними. Нажав на серединной точке делителя, можно скрыть интерфейс с вкладками. При нажатии на кнопку в средней части главного окна приложения можно увидеть заданный в настоящее время КА. Как уже было сказано выше, система позволяет осуществлять шаги вперед и назад. Если было сделано достаточное количество шагов алгоритма, нажмите на кнопку «!» для получения ответа о текущем векторе состояния (рис. 18). В зависимости от КА будет выдан соответствующий результат. Рис. 16, а. Поле представления оператора суперпозиции Квантовый оператор визуализации позволяет отображать структуру матриц используемых квантовых операторов в двумерном представлении (рис. 16а) и в 3D-представлении (рис. 16б). Если оператор состоит из тензорного произведения небольших операторов, то существует возможность просмотра подблоков тензорных произведений. 3D-визуализатор позволяет изменять параметры просмотра: увеличить или уменьшить изображение, а также вращать его. Рис. 16, б. 3В-представление оператора суперпозиции для поискового квантового алгоритма Гровера с 3 кубитами в приложении квантового эмулятора Рис. 16, в. 3 D-представление оператора квантовой корреляции для поискового квантового алгоритма Гровера с 3 кубитами в приложении квантового эмулятора Рис. 16,г. 3D-представление оператора интерференции для поискового квантового алгоритма Гровера с 3 кубитами в приложении квантового эмулятора Рис. 17. Редактор входных функций приложения КА-эмулятора (поисковый квантовый алгоритм Гровера с 3 кубитами) Редактор входных функций позволяет автоматизировать процесс кодирования оператора квантовой корреляции, как это было описано в предыдущих разделах. Для поискового квантового алгоритма Гровера можно закодировать функции, которые имеют более чем один положительный вывод. Рис. 18. 3D-график вектора состояния для поискового квантового алгоритма Гровера с 3 кубитами после выполнения 2-х итераций Рис. 19. Окно выдачи ответа в случае, когда алгоритм Гровера выполнил достаточное количество шагов Рис. 20. Динамика энтропии Шеннона после выполнения 31-го шага поискового квантового алгоритма Гровера Рисунки 21 и 22 показывают начальное (рис. 21) и конечное (рис. 22) квантовое состояние в случаях использования алгоритмов Дойча-Джодза, Саймона и Шора. Рис. 21. Начальное состояние КА-эмулятора при моделировании алгоритмов Дойча-Джодза (а), Саймона (b) и Шора (с) Рис. 22. Конечное состояние КА-эмулятора при моделировании алгоритмов Дойча-Джодза (а), Саймона (b) и Шора (c) Пример кодирования входных функции и соответствующее 3D-представление оператора запутанности для алгоритмов Дойча-Джодза, Саймона и Шора представлены на рис. 23. Рис. 23. Сбалансированный вход в КА Дойча-Джодза. Функция (а) и соответствующий оператор запутанности (b); вход в КА Саймона и Шора (с) и соответствующий оператор запутанности (d) Рисунок 24 демонстрирует динамику энтропии Шеннона в моделируемых квантовых алгоритмов после нескольких итераций алгоритма. Понятно, что ее минимум достигается в состояниях с минимальной неопределенностью, независимо от алгоритма имитации. Рис. 24. Динамика энтропии Шеннона: КА Дойча-Джодза (а), КА Саймона (b), КА Шора (c). Результаты моделирования представленных КА представлены на рисунке 5.41, после работы интерпретатора. Result Collected vectors: 0,1 Value of s: 2,4,6 Collected vectors: 0,4,1,2,3,5,6,7 Value of I: 1 Period: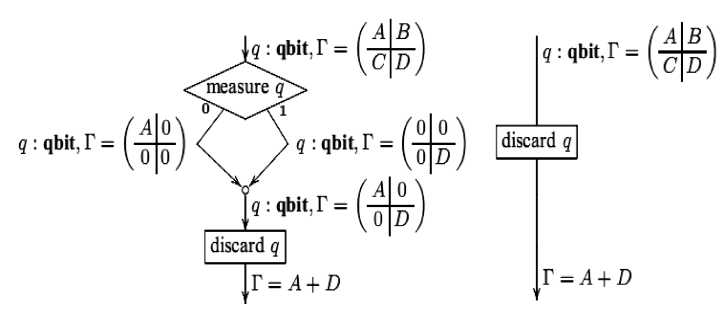
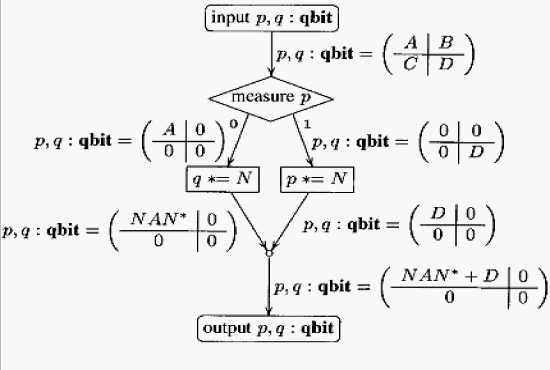
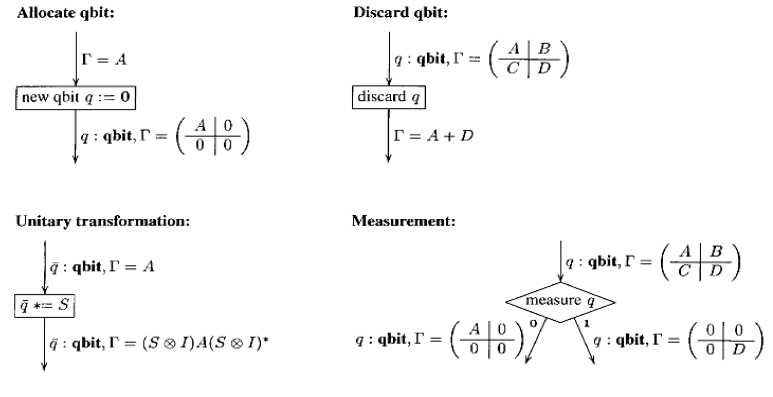
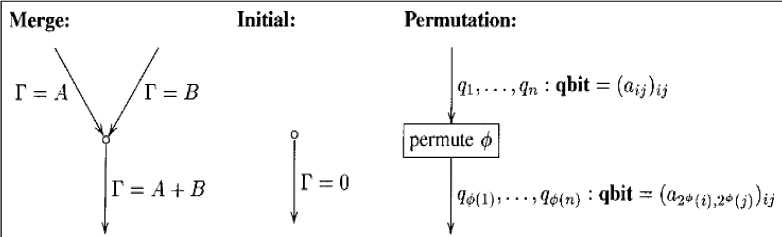
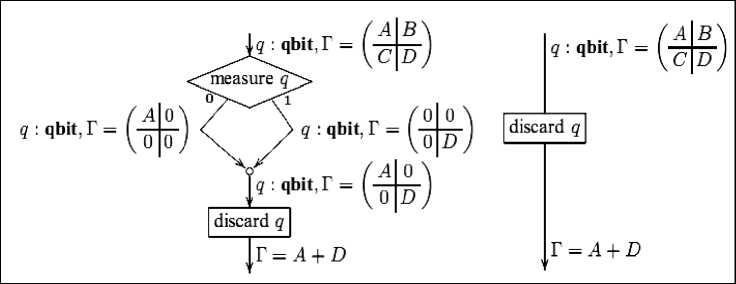
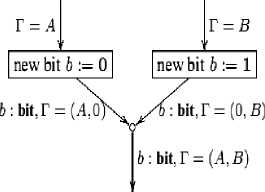
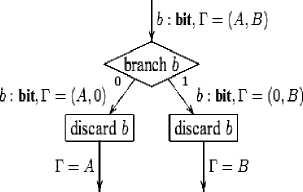
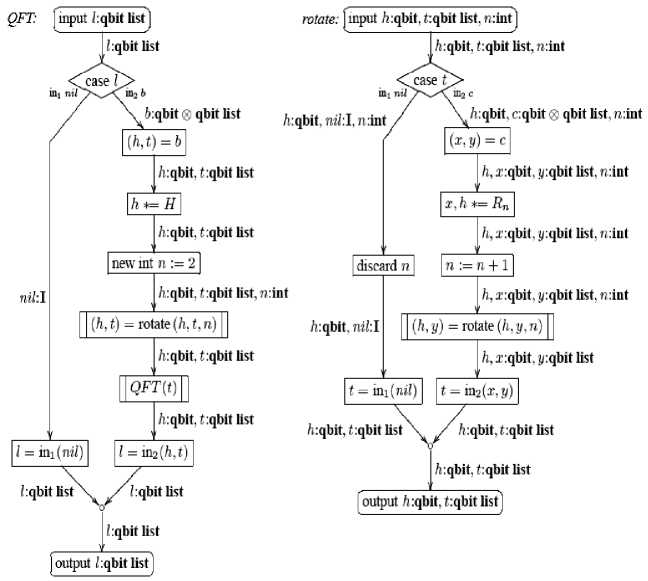
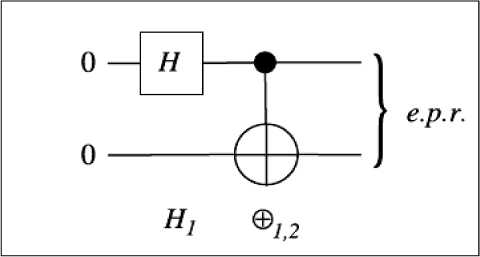


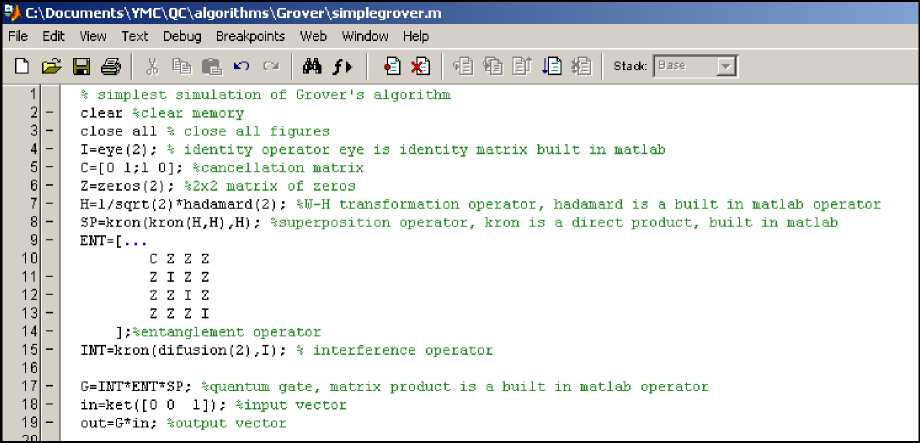
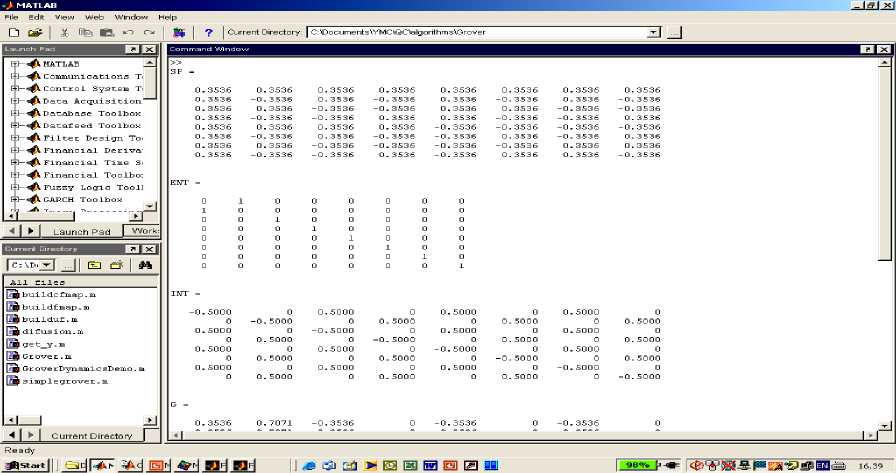
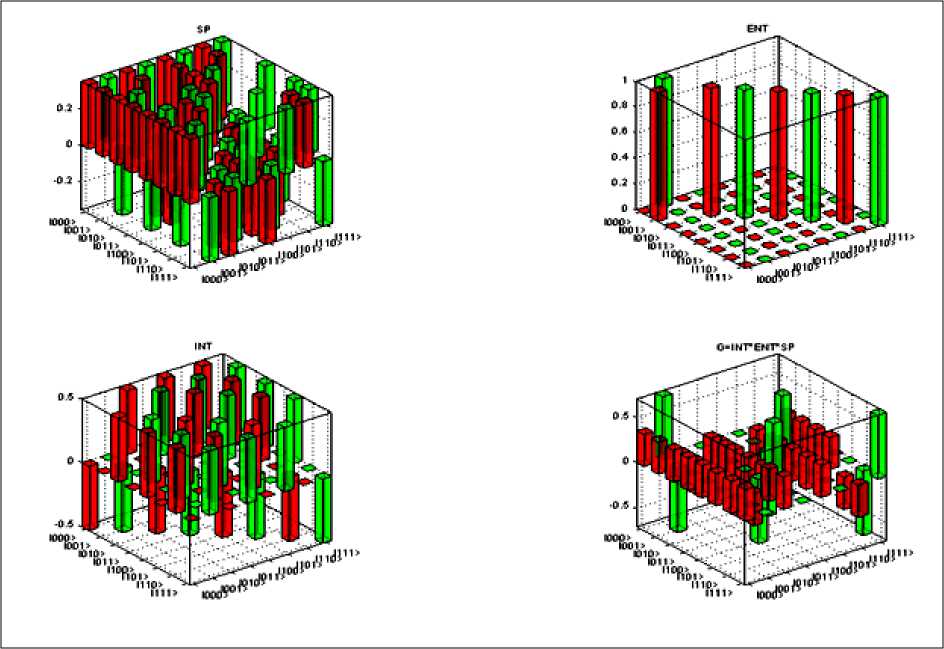
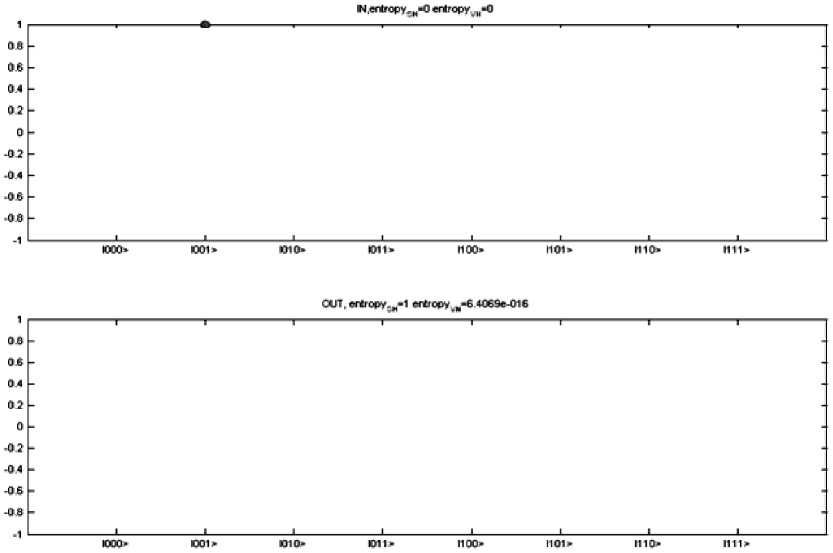
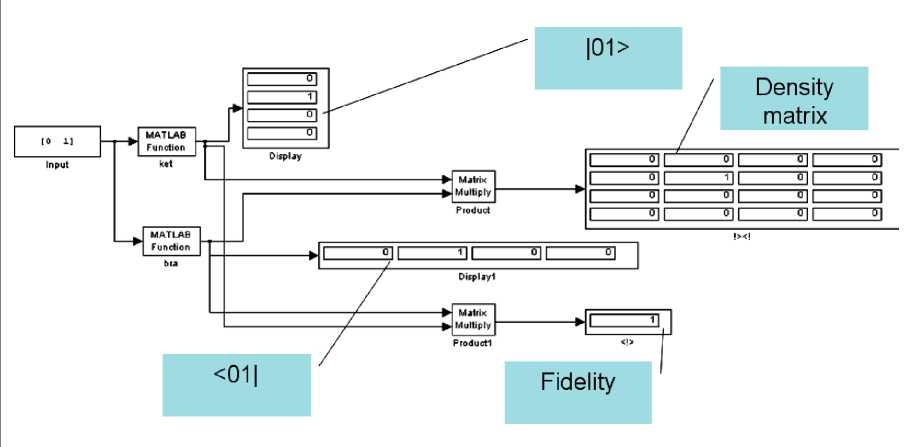
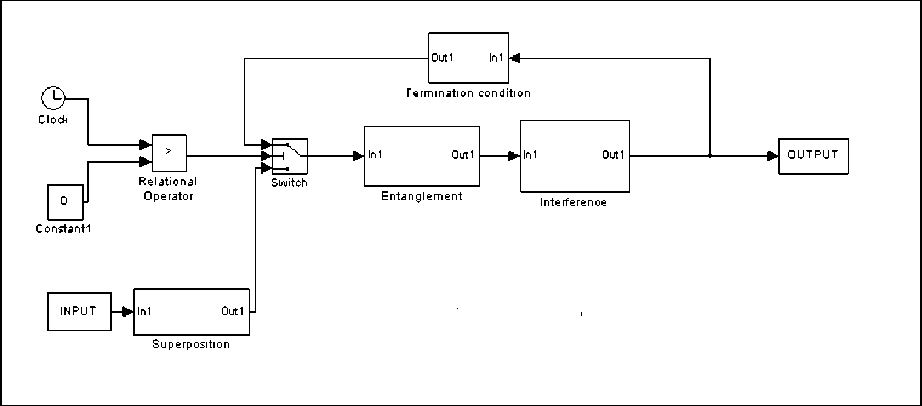
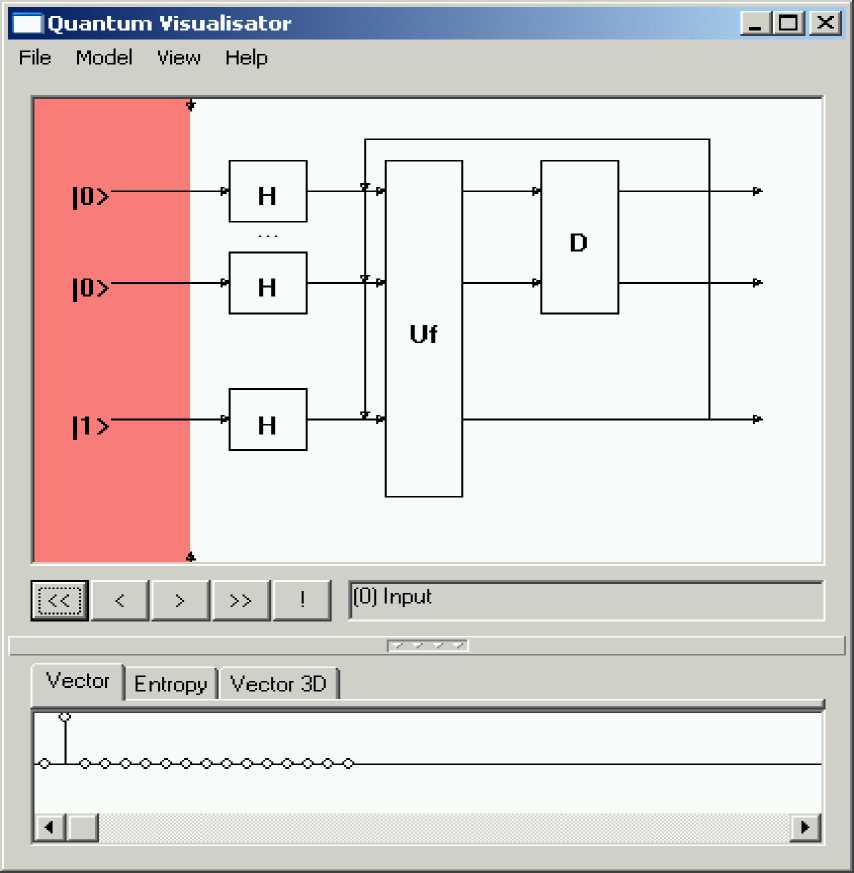
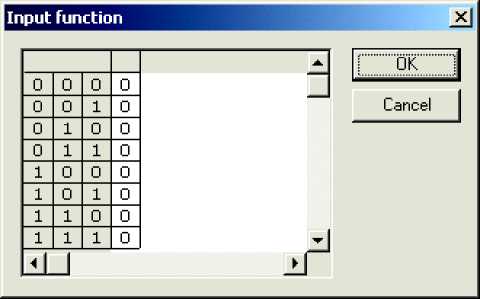
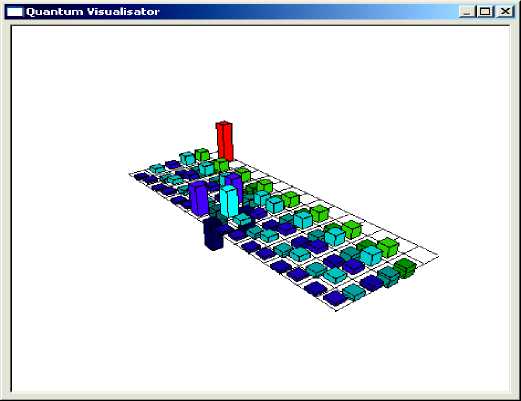

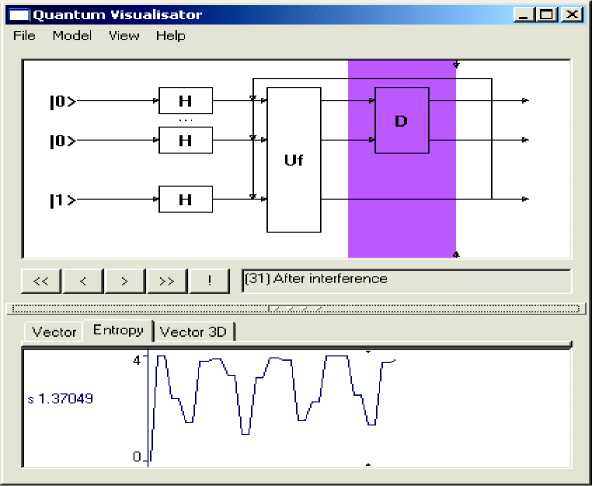
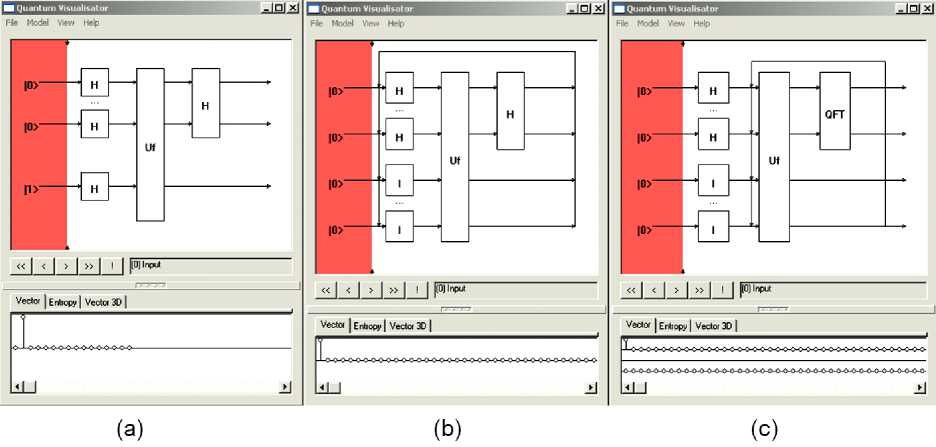
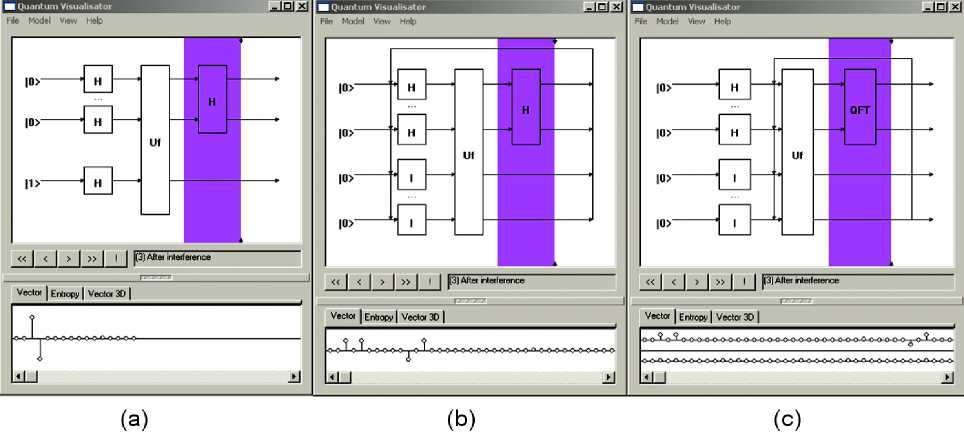
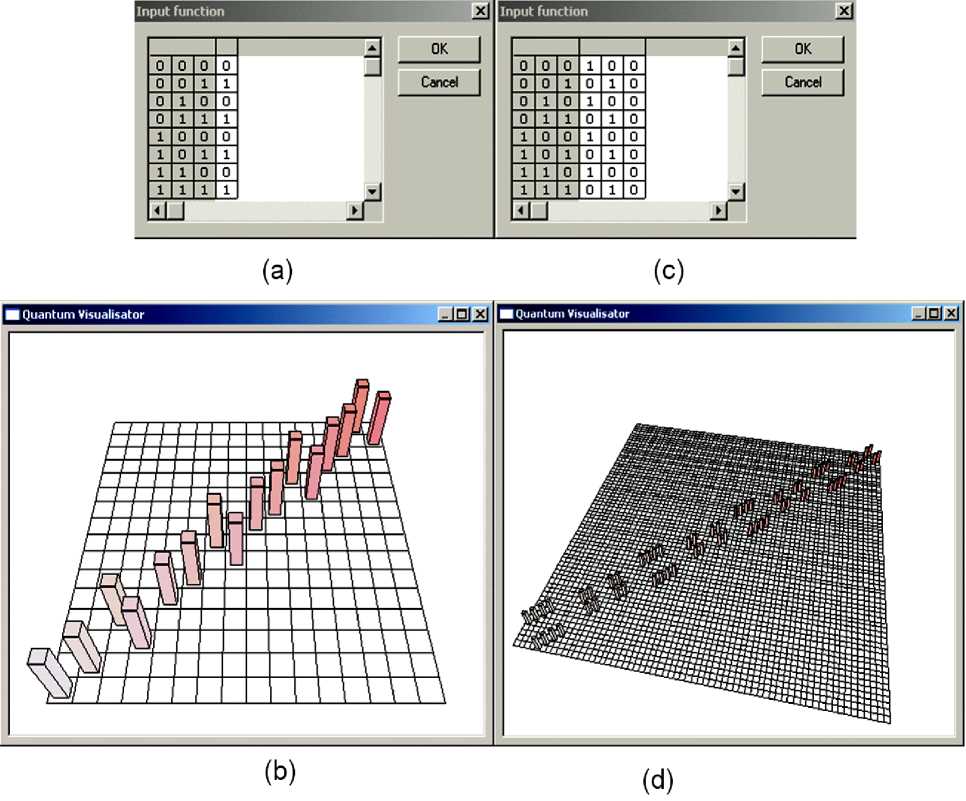
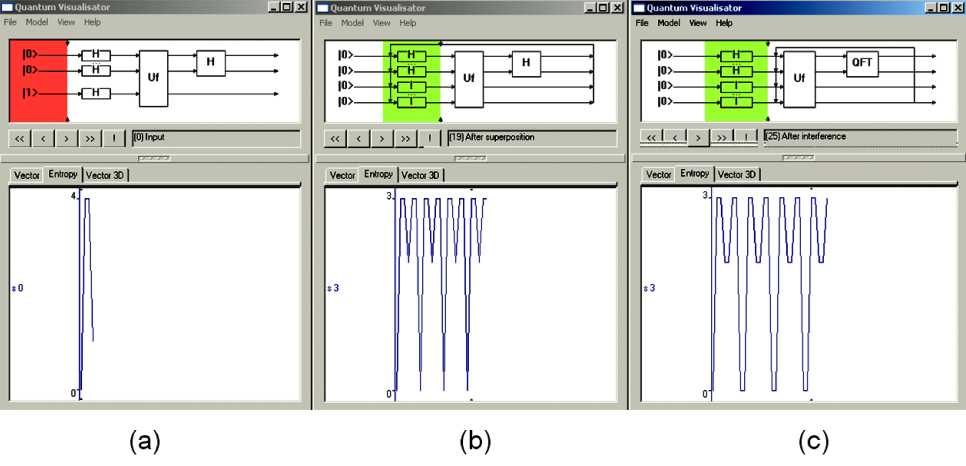


Список литературы Квантовая релятивистская информатика. Ч. 4: элементы квантовой релятивистской теории информации и квантового программирования
- Kitaev A.Yu., Shen A.H., Vyaly M.N. Classical and quantum computation. - N.Y.: AMS, 2002.
- Brylinski F.K. and Chen G. (Eds). Mathematics of quantum computation. - Computational Mathematics Series. - CRC Press Co, 2002.
- Ulyanov S.V., Litvintseva L.V., Ulyanov I.S. and Ulyanov S.S. Quantum information and quantum computational intelligence: Quantum decision making and search algorithms // Note del Polo Ricerca, Università degli Studi di Milano (Polo Didattico e di Ricerca di Crema). - Milan, 2005. - Vols. 84, 85.
- Stenholm S. and Suominen K.-A. Quantum approach to informatics. - Wiley- Interscience. J. Wiley&Sons, Inc, 2005.
- EDN: SSSFMN
- Marinescu D.C. and Marinescu G.M. Approaching quantum computing. - Pearson Prentice Hall, New Jersey, 2005.


