Квантово-химический расчет молекул некоторых соединений с малыми циклами методом AM1
Автор: Бабкин Владимир Александрович, Быкова Татьяна Сергеевна, Фомичев Валерий Тарасович, Наумова Галина Алексеевна, Заиков Геннадий Ефремович
Журнал: НБИ технологии @nbi-technologies
Рубрика: Технико-технологические инновации
Статья в выпуске: 1 (8), 2013 года.
Бесплатный доступ
Впервые выполнен квантово-химический расчет молекулы этилциклопропана, бицикло[6,-1,0]нонана,1-хлор-1-бром-2,2-диметилциклопропана методом AM1 с оптимизацией геометрии по всем параметрам стандартным градиентным методом. Получено оптимизированное геометрическое и электронное строение этих соединений. Теоретически оценена его кислотная сила (28 14).
Квантово-химический расчет, метод am1, этилциклопропан, бицикло[6, 0]нонан, 1-хлор-1-бром-2, 2-диметилциклопропан, кислотная сила
Короткий адрес: https://sciup.org/14968272
IDR: 14968272 | УДК: 547.854.83:544.183.25
Текст научной статьи Квантово-химический расчет молекул некоторых соединений с малыми циклами методом AM1
Целью настоящей работы является выполненный методом AM1 с оптимизацией геометрии по всем параметрам стандартным градиентным методом, встроенным в PC GAMESS [15], квантово-химический расчет молекул этилциклопропана, бицикло[6,1,0]нонана,1-хлор-1-бром-2,2-ди-метилциклопропана, в приближении изолированных молекул в газовой фазе, и теоретическая оценка его кислотной силы. Для визуального представления моделей молекул использовалась известная программа MacMolPlt [14].
Результаты расчетов
Оптимизированное геометрическое и электронное строение, общая энергия, электронная энергия молекул этилциклопропана, бицикло[6,1,0]нонана,1-хлор-1-бром-2,2-ди-метилциклопропана получены методом AM1 и показаны на рисунках 1–3 и в таблицах 1– 4. Используя известную формулу рКа=47.74 – 154.949 qmaxH+ [11; 13], с успехом используемую, например, в [1-10] (+0,12 < qmaxH+ < +0,13 - максимальный заряд на ато- ме водорода, рКа – универсальный показатель кислотности, см. табл. 1), находим значение кислотной силы.
Таким образом, нами впервые выполнен методом AM1 квантово-химический расчет молекул этилциклопропана, бицикло[6,1,0]но-нана,1-хлор-1-бром-2,2-диметилциклопропана. Получено оптимизированное геометрическое и электронное строение этих соединений. Теоретически оценена их кислотная сила, значение которой равно 28 < pKa < 29. Установлено, что молекулы этилциклопропана, бицикло[6,1,0]но-нана,1-хлор-1-бром-2,2-диметилциклопропана относятся к классу очень слабых Н-кислот: pKa >14 (см. табл. 4).
Н14
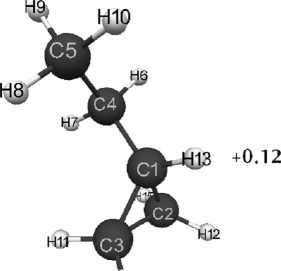
Рис. 1. Геометрическое и электронное строение молекулы этилциклопропана
(Е0= -75 002 кДж/моль, Еэл= -303 023 кДж/моль)
Таблица 1
валентные углы и заряды на атомах молекулы этилциклопропана
|
Длины связей |
R,A |
Валентные углы |
Град |
Атом |
Заряды на атомах молекулы |
|
C(2)-C(1) |
1.51 |
C(1)-C(2)-C(3) |
60 |
C(1) |
-0.16 |
|
C(3)-C(2) |
1.49 |
C(2)-C(3)-C(1) |
60 |
C(2) |
-0.21 |
|
C(1)-C(3) |
1.51 |
C(3)-C(1)-C(2) |
60 |
C(3) |
-0.21 |
|
C(1)-C(4) |
1.49 |
C(2)-C(1)-C(4) |
119 |
C(4) |
-0.13 |
|
C(4)-C(5) |
1.51 |
C(1)-C(4)-C(5) |
112 |
C(5) |
-0.21 |
|
H(6)-C(4) |
1.12 |
C(1)-C(4)-H(6) |
109 |
H(6) |
0.08 |
|
H(7)-C(4) |
1.12 |
C(1)-C(4)-H(7) |
110 |
H(7) |
0.08 |
|
H(8)-C(5) |
1.12 |
C(4)-C(5)-H(8) |
111 |
H(8) |
0.08 |
|
H(9)-C(5) |
1.12 |
C(4)-C(5)-H(9) |
110 |
H(9) |
0.07 |
|
H(10)-C(5) |
1.12 |
C(4)-C(5)-H(10) |
111 |
H(10) |
0.07 |
|
H(11)-C(3) |
1.1 |
C(1)-C(3)-H(11) |
119 |
H(11) |
0.11 |
|
H(12)-C(2) |
1.1 |
C(1)-C(2)-H(12) |
119 |
H(12) |
0.11 |
|
H(13)-C(1) |
1.11 |
C(2)-C(1)-H(13) |
118 |
H(13) |
0.12 |
|
H(14)-C(3) |
1.1 |
C(2)-C(3)-H(14) |
119 |
H(14) |
0.12 |
|
H(15) -C(2) |
1.1 |
C(3)-C(2)-H(15) |
119 |
H(15) |
0.12 |
Оптимизированные длины связей,
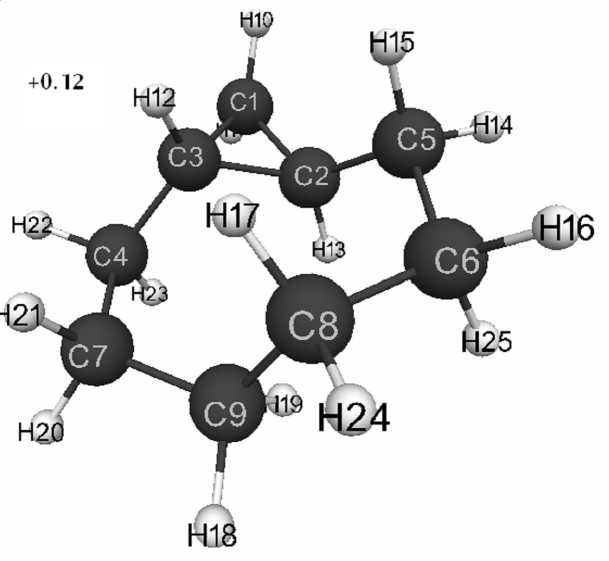
Рис. 2. Геометрическое и электронное строение молекулы бицикло[6,1,0]нонана (Е0= -132 441 кДж/моль, Еэл= -752 772 кДж/моль)
Таблица 2
Оптимизированные длины связей, валентные углы и заряды на атомах молекулы бицикло[6,1,0]нонана
|
Длины связей |
R,A |
Валентные углы |
Град |
Атом |
Заряды на атомах молекулы |
|
C(2)-C(1) |
1.51 |
C(1)-C(2)-C(3) |
60 |
C(1) |
-0.2 |
|
C(3)-C(2) |
1.51 |
C(2)-C(3)-C(1) |
60 |
C(2) |
-0.17 |
|
C(1)-C(3) |
1.51 |
C(3)-C(1)-C(2) |
61 |
C(3) |
-0.16 |
|
C(3)-C(4) |
1.49 |
C(1)-C(3)-C(4) |
126 |
C(4) |
-0.13 |
|
C(2)-C(5) |
1.49 |
C(1)-C(2)-C(5) |
126 |
C(5) |
-0.13 |
|
C(5)-C(6) |
1.52 |
C(2)-C(5)-C(6) |
110 |
C(6) |
-0.15 |
|
C(4)-C(7) |
1.52 |
C(3)-C(4)-C(7) |
110 |
C(7) |
-0.15 |
|
C(6)-C(8) |
1.52 |
C(5)-C(6)-C(8) |
114 |
C(8) |
-0.15 |
|
C(8)-C(9) |
1.52 |
C(4)-C(7)-C(9) |
114 |
C(9) |
-0.15 |
|
H(10)-C(1) |
1.11 |
C(3)-C(1)-H(10) |
118 |
H(10) |
0.11 |
|
H(11)-C(1) |
1.1 |
C(3)-C(1)-H(11) |
120 |
H(11) |
0.11 |
|
H(12)-C(3) |
1.11 |
C(1)-C(3)-H(12) |
116 |
H(12) |
0.12 |
|
H(13)-C(2) |
1.11 |
C(1)-C(2)-H(13) |
116 |
H(13) |
0.12 |
|
H(14)-C(5) |
1.12 |
C(2)-C(5)-H(14) |
110 |
H(14) |
0.08 |
|
H(15)-C(5) |
1.12 |
C(2)-C(5)-H(15) |
110 |
H(15) |
0.08 |
|
H(16)-C(6) |
1.12 |
C(5)-C(6)-H(16) |
108 |
H(16) |
0.07 |
|
H(17)-C(8) |
1.12 |
C(6)-C(8)-H(17) |
109 |
H(17) |
0.08 |
|
H(18)-C(9) |
1.12 |
C(8)-C(9)-H(18) |
108 |
H(18) |
0.07 |
|
H(19) -C(9) |
1.12 |
C(8)-C(9)-H(19) |
110 |
H(19) |
0.08 |
|
H(20)-C(7) |
1.12 |
C(9)-C(7)-H(20) |
109 |
H(20) |
0.07 |
|
H(21)-C(7) |
1.12 |
C(9)-C(7)-H(21) |
110 |
H(21) |
0.08 |
|
H(22)-C(4) |
1.12 |
C(3)-C(4)-H(22) |
110 |
H(22) |
0.08 |
|
H(23) -C(4) |
1.12 |
C(3)-C(4)-H(23) |
110 |
H(23) |
0.08 |
|
H(24)-C(8) |
1.12 |
C(6)-C(8)-H(24) |
108 |
H(24) |
0.07 |
|
H(25)-C(6) |
1.12 |
C(5)-C(6)-H(25) |
109 |
H(25) |
0.08 |
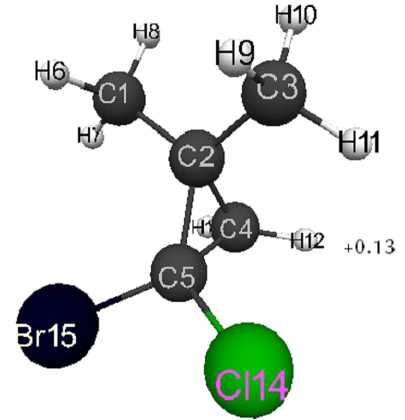
Рис. 3. Геометрическое и электронное строение молекулы 1-хлор-1-бром-2,2-диметилциклопропана (Е0= -142 472 кДж/моль, Еэл= -537 075 кДж/моль)
Таблица 3
Оптимизированные длины связей, валентные углы и заряды на атомах молекулы 1-хлор-1-бром-2,2-диметилциклопропана
|
Длины связей |
R,A |
Валентные углы |
Град |
Атом |
Заряды на атомах молекулы |
|
C(2)-C(1) |
1.5 |
C(5)-C(2)-C(1) |
119 |
C(1) |
-0.19 |
|
C(4)-C(2) |
1.51 |
C(5)-C(4)-C(2) |
61 |
C(2) |
-0.06 |
|
C(2)-C(3) |
1.5 |
C(1)-C(2)-C(3) |
113 |
C(3) |
-0.19 |
|
C(5)-C(4) |
1.51 |
C(1)-C(2)-C(4) |
119 |
C(4) |
-0.18 |
|
C(2)-C(5) |
1.53 |
C(2)-C(4)-C(5) |
61 |
C(5) |
-0.17 |
|
H(6)-C(1) |
1.12 |
C(2)-C(1)-H(6) |
110 |
H(6) |
0.09 |
|
H(7)-C(1) |
1.12 |
C(2)-C(1)-H(7) |
112 |
H(7) |
0.09 |
|
H(8)-C(1) |
1.12 |
C(2)-C(1)-H(8) |
110 |
H(8) |
0.09 |
|
H(9)-C(3) |
1.12 |
C(2)-C(3)-H(9) |
110 |
H(9) |
0.09 |
|
H(10)-C(3) |
1.12 |
C(2)-C(3)-H(10) |
110 |
H(10) |
0.09 |
|
H(11)-C(3) |
1.12 |
C(2)-C(3)-H(11) |
112 |
H(11) |
0.09 |
|
H(12)-C(4) |
1.11 |
C(2)-C(4)-H(12) |
119 |
H(12) |
0.13 |
|
H(13)-C(4) |
1.11 |
C(2)-C(4)-H(13) |
119 |
H(13) |
0.13 |
|
Cl(14)-C(5) |
1.73 |
C(4)-C(5)-Cl(14) |
118 |
Cl(14) |
-0.03 |
|
Br(15)-C(5) |
1.91 |
C(2)-C(5)-Br(15) |
121 |
Br(15) |
0.04 |
Таблица 4
Показатели молекул, полученные методом АМ1
Список литературы Квантово-химический расчет молекул некоторых соединений с малыми циклами методом AM1
- Бабкин, В. А. Квантово-химический расчет молекулы изобутилена методом MNDO/В. А. Бабкин, Д. С. Андреев//Квантово-химический расчет уникальных молекулярных систем: сб. науч. ст. -Волгоград: Изд-во ВолГУ 2010. -Т. 1. -С. 176-177.
- Бабкин, В. А. Квантово-химический расчет молекулы 2-метилбутена-1 методом MNDO/В. А. Бабкин, Д. С. Андреев//Квантово-химический расчет уникальных молекулярных систем: сб. науч. ст. -Волгоград: Изд-во ВолГУ, 2010. -Т. 1. -С. 177-179.
- Бабкин, В. А. Квантово-химический расчет молекулы 2-метилбутена-2 методом MNDO/В. А. Бабкин, Д. С. Андреев//Квантово-химический расчет уникальных молекулярных систем: сб. науч. ст. -Волгоград: Изд-во ВолГУ, 2010. -Т. 1. -С. 179-180.
- Бабкин, В. А. Квантово-химический расчет молекулы 2-метилпентена-1 методом MNDO/В. А. Бабкин, Д. С. Андреев//Квантово-химический расчет уникальных молекулярных систем: сб. науч. ст. -Волгоград: Изд-во ВолГУ, 2010. -Т. 1. -С. 181-182.
- Бабкин, В. А. Квантово-химический расчет молекулы 2-этилбутена-1 методом MNDO/В. А. Бабкин, Д. С. Андреев//Квантово-химический расчет уникальных молекулярных систем: сб. науч. ст. -Волгоград: Изд-во ВолГУ, 2010. -Т. 1. -С. 183-185.
- Бабкин, В. А. Квантово-химический расчет молекулы мономера катионной полимеризации гексен-1 методом MNDO/В. А. Бабкин, В. Ю. Дмитриев, Г. Е. Заиков//Квантово-химический расчет уникальных молекулярных систем: сб. науч. ст. -Волгоград: Изд-во ВолГУ, 2010. -Т. 1. -С. 93-95.
- Бабкин, В. А. Квантово-химический расчет молекулы мономера катионной полимеризации гептен-1 методом MNDO/В. А. Бабкин, В. Ю. Дмитриев, Г. Е. Заиков//Квантово-химический расчет уникальных молекулярных систем: сб. науч. ст. -Волгоград: Изд-во ВолГУ, 2010. -Т. 1. -С. 95-97.
- Бабкин, В. А. Квантово-химический расчет молекулы мономера катионной полимеризации декен-1 методом MNDO/В. А. Бабкин, В. Ю. Дмитриев, Г. Е. Заиков//Квантово-химический расчет уникальных молекулярных систем: сб. науч. ст. -Волгоград: Изд-во ВолГУ, 2010. -Т. 1. -С. 97-99.
- Бабкин, В. А. Квантово-химический расчет молекулы мономера катионной полимеризации нонен-1 методом MNDO/В. А. Бабкин, В. Ю. Дмитриев, Г. Е. Заиков//Квантово-химический расчет уникальных молекулярных систем: сб. науч. ст. -Волгоград: Изд-во ВолГУ, 2010. -Т. 1. -С. 99-102.
- Бабкин, В. А. Квантово-химический расчет молекулы мономера катионной полимеризации октен-1 методом MNDO/В. А. Бабкин, В. Ю. Дмитриев, Г. Е. Заиков//Квантово-химический расчет уникальных молекулярных систем: сб. науч. ст. -Волгоград: Изд-во ВолГУ, 2010. -Т. 1. -С. 103-104.
- Бабкин, В. А. О корреляционной зависимости универсального показателя кислотности с максимальным зарядом на атоме водорода Н-кислот. Метод АМ1/В. А. Бабкин и [др.]. -Вестник Казанского технологического университета. -2012. -№ 10. -С. 15-19.
- Кеннеди, Дж. Катионная полимеризация олефинов/Дж. Кеннеди. -М., 1978. -431 с.
- Babkin, V.A./V. A. Babkin [et al.]//Oxidation communication, 21. -1998. -№ 4. -P. 454-460.
- Bode, B. M. Mol. Graphics Mod., 16/B. M. Bode and M. S. Gordon J. -Amer. Chem. Soc., 1998. -P. 133-138.
- Shmidt, M. W. J. Comput/M. W. Shmidt [et al.]. -Chem. 14.-Chem. Rev. Lett., 1993. -P. 1347-1363.


