Квантовое программирование. Ч.1: анализ средств разработки

За последние годы интерес к квантовым вычислениям постоянно растёт. Появляется всё больше исследовательских групп, компании и правительство вкладывают большие средства в исследования в области квантовых вычислений. Возникает уверенность, что появление квантового компьютера – это дело времени. Но что тогда с ним делать? Прежде всего нужны доказанные алгоритмы, задачи, которые квантовый компьютер может решить, в отличие от классического. Таким образом возрос интерес к квантовым компьютерам после публикации работы Шора [1] и Гровера [2].

Для классического компьютера существует множество языков программирования, при помощи которых можно создать программу различной сложности. Очевидно, что для программирования на квантовом компьютере понадобятся новые, квантовые языки программирования. Однако отсутствие квантового компьютера – не проблема. Для проведения исследований разработаны симуляции квантовых явлений на классическом компьютере.

В начале XXI века были популярны идеи о создании отдельных языков для квантового программирования, затем начали разрабатывать библиотеки для классических языков программирования:  Golang, Python, C++ и квантовые языки программирования, которые выполняются из классической программы. Это может быть крайне полезно, т.к. в крупном классическом приложении можно сделать отдельный сервис, решение какой-то определённой задачи, который будет написан на классическом языке, но будет вызывать квантовую программу.

Главная особенность применения на классическом компьютере симуляции квантовых вычислений в том, что даже в таком виде алгоритмы могут дать преимущество, по сравнению с классическими подходами [3, 5].

Цель серии статьей – выбор подходящего средства разработки квантовых алгоритмов на классическом компьютере. В этой статье изучаются возможности Q# в том числе будут реализованы программы, демонстрирующие: суперпозицию, запутанность и квантовую телепортацию. В дальнейших статьях будет проводиться анализ и сравнение различных квантовых языков программирования и библиотек для классических языков программирования. Одно из главных требований - написанную на выбранном языке программирования программу должно быть возможно интегрировать в другие системы.

Квантовые языки программирования и их симуляция

Quantum Computation Language (QCL)

QCL - один из первых разработанных квантовых языков программирования, его синтаксис идентичен языку C . Язык предоставляет достаточно много возможностей по знакомству с квантовыми алгоритмами и их реализацией. Однако последняя версия языка выходила в 2014 году, подобное решение не подходит для поставленных задач.

Аналогичные проблемы, как с QCL, в языке Q от Kx Systems , который реализован как расширение языка C++ . В нём реализованы классы для основных квантовых операций. В языке не так много возможностей, он не обновлялся с 2018 года и тоже не подходит для поставленных задач. Более подробное сравнение этих языков можно изучить в статье [4].

Q#

Q# - предметно-ориентированный язык, разрабатываемый компанией Microsoft , как часть Quantum Development Kit , который включает в себя квантовый симулятор, способный выполнять код Q# . Основной особенностью Q# является возможность создавать и использовать кубиты для алгоритмов. Поэтому появляется способность запутывать и вводить суперпозицию в кубиты через Controlled NOT и Hadamard гейты, а также Toffoli, Pauli X, Y, Z гейты и многие другие. Квантовый симулятор способен обрабатывать 32 кубита на пользовательском компьютере и до 40 кубитов в облаке Azure.

Quantum Development Kit состоит из языка программирования Q# , API для языков Python и .NET. Благодаря этому можно создать основную программу на языке Python или C# , вызывающую операции Q#. Также имеется возможность использовать Jupyter Notebook для создания интерактивных учебников.

Знакомство с Q# можно начать с кубита [6]. Кубит находится в состоянии суперпозиции, а его измерение возвращает классическое двоичное значение |0) или |1), при измерении он также переходит из состояния суперпозиции в одно из классических состояний. Также несколько кубитов могут находиться в состоянии запутанности, в таком случае при измерении одного из запутанных кубитов можно получить сведения о состоянии другого.

Рассмотрим, как на языке Q# и Python можно реализовать программу, в которой необходимо для заданного количества симуляций и для заданного желаемого измеренного значения кубита подсчитать сколько раз и какое значение принимал кубит в ходе этих симуляций.

Т.к. при измерении кубита он может принять значение |0) или |1), то необходимо написать собственную квантовую операцию, которая будет проверять значение кубита и в случае несовпадения будет инвертировать его.

operation Set(desired : Result, q1 : Qubit) : Unit { if (desired != M(q1)) {

X(q1);

}

}

Так можно создать указанную операцию. В Q# операцией называется подпрограмма, которая содержит квантовые операции. В виде кортежа в круглых скобках задаются аргументы операции, возвращаемый тип задаётся после двоеточия. Если операция не должна ничего возвращать, то для неё указывается возвращаемый тип Unit. В данной операции 2 аргумента: desired с типом Result (измеренное значение кубита) и сам Qubit. Далее используется квантовая операция M, которая измеряет состояние кубита. Если измеренное состояние совпадает с желаемым, то ничего не делаем с кубитом, если же они не совпадают, то применяем квантовую операцию X, которая инвертирует состояние кубита. Квантовая операция также называется квантовым гейтом.

operation BellState(count : Int, desiredValue : Result) :  (Int, Int) { mutable numOnes = 0;

Set(desiredValue, qubit);

let res = M(qubit);

if (res == One) { set numOnes += 1;

}

}

Set(Zero, qubit);

} return (count-numOnes, numOnes);

}

Далее представлен код операции BellState , которая принимает 2 аргумента: количество раз, которое будет запускаться код и измеряться кубит, и желаемое значение кубита. Операция возвращает два значение Int : сколько раз кубит был равен |0〉 и |1〉. Чтобы в Q# создать изменяемую переменную, необходимо использовать mutable – в данной операции эта переменная будет использоваться для подсчёта количества полученных единиц. Все переменные по умолчанию неизменяемые, let означает объявление неизменяемое переменной. Чтобы изменить mutable переменную, необходимо использовать set. Тип переменной объявлять не требуется.

Using – особая операция в Q# , она выделяет кубиты для использования в блоке. Все кубиты выделяются и освобождаются динамически, а не фиксируются на протяжении работы всего алгоритма. В конце блока оператор освобождает кубиты.

В цикле происходит присваивание кубиту желаемого значения при помощи ранее написанной операции Set , затем происходит измерение значения полученного кубита. Если оно равно |1〉, то numOnes увеличивается на 1, а затем восстанавливается известное состояние кубита (|0〉).

Используем написанную операцию BellState для симуляции 1000 раз с желаемым значением кубита равным |0〉. BellState возвращает количество кубитов, которые приняли значение |0〉 и |1〉, а потом эти значения печатаются на экран. В ходе выполнения этой программы кубит 1000 раз будет равен |0〉, если желаемое значение кубита |0〉, аналогично будет для |1〉, если желаемое значение поменять на |1〉.

Пока поведение кода программы не отличается от классических вычислений. Применим гейт Адамара, чтобы он перевёл кубит в значение суперпозиции.

Set(desiredValue, qubit);

H(qubit);

let res = M(qubit);

При нескольких запусках программы получились следующие значения:

0s=503 1s=497

0s=485 1s=515

0s=513 1s=487

Благодаря состоянию суперпозиции статистически в половине случае значение кубита равно |0〉, в другой половине – |1〉 (например, для 1 млн. симуляций: 0s=500115 1s=499885).

Чтобы в Q# написать запутанность кубитов (уже необходимо несколько кубитов) необходимо присвоить кубиту начальное состояние, а затем переместить в состояние суперпозиции при помощи гейта Адамара. Прежде чем измерить первый кубит необходимо применить гейт CNOT. Благодаря этой операции второй кубит инвертируется, если первый кубит имеет значение |0〉. Эти два кубита будут запутанными. Распределение вероятности первого кубита осталась такой же (по 50%), но второй кубит теперь всегда будет в таком же состоянии, как и первый кубит. Благодаря CNOT появилась запутанность кубитов, любые изменения одного влияют на другой.

operation BellState(count : Int, desiredValue : Result) :  (Int, Int, Int) { mutable numOnes =0;

mutable match =0;

Set(desiredValue, qubit0);

Set(Zero, qubit1);

H(qubit);

CNOT(qubit0, qubit1);

let res = M(qubit0);

if (M(qubit1) == res) { set match +=1;

} if (res == One){ set numOnes +=1;

}

}

Set(Zero, qubit0);

Set(Zero, qubit1);

} return (count-numOnes, numOnes, match);

}

Для того, чтобы запрограммировать в Q# данное поведение необходимо использовать 2 кубита, добавить Set для инициализации и сброса кубита, а также добавить гейт CNOT . Также необходимо добавить 3-ий возвращающийся аргумент в операции BellState , добавить переменную match, в которой будем подсчитывать количество совпадений полученного значения обоих кубитов.

Также необходимо дополнить Python программу. Результат будет примерно следующий: 0s=511 1s=489 match=1000. Как видим, во всех 1000 симуляций значения обоих кубитов совпали.

Квантовая телепортация – перемещение квантового состояния из одного места в другое без необходимости перемещать физические частицы. Это возможно из-за ранее рассмотренной квантовой запутанности между отправляющим и получающим местоположениями по классическому каналу связи.

В примере будет рассмотрена телепортация классического сообщения ( true , false ). Для начала необходимо написать квантовую операцию телепортации, которая отправляет один кубит в целевой кубит при помощи телепортации. Важно отметить, что состояние кубита сообщения ( message) будет разрушено. Операция должна принимать 2 аргумента, кубита: message – кубит, чьё состояние будет отправлено, target – кубит, в первоначальном состоянии |0〉, куда будет отправлено состояние message . Операция ничего не будет возвращать.

operation Teleport (message : Qubit, target : Qubit) : Unit { using (register = Qubit()) {

// Создание квантовой запутанности

H(register);

CNOT(register, target);

// Кодирование сообщения в запутанную пару

CNOT(message, register);

H(message);

// Измерение кубитов для извлечения классических данных

// которые необходимы для правильного декодирования сообщения

// в целевой кубит let data1 = M(message);

let data2 = M(register);

// Декодирование сообщения, применяя коррекцию на

// целевой кубит.

// Для этого используется встроенный оператор MResetZ

// из пакета Microsoft.Quantum.Measurement

// для сброса кубитов по мере продвижения if (MResetZ(message) == One) { Z(target); }

// Также используется Q# функция IsResultOne для записи

// шагов коррекции. Функция полезная для создания условий

// с другими функциями и операциями.

if (IsResultOne(MResetZ(register))) { X(target); } }

}

Далее создаётся операция, которая позволяет использовать операция телепортации ( Teleport) для отправки ненаблюдаемого классического сообщения из исходного кубита в целевой кубит, посылая конкретную классическую информацию из одного кубита в другой (целевой) кубит. Операция будет использоваться в классического программе на языке Python , принимает один аргумент message типа bool и возвращает также значение типа bool . Если отправляемое сообщение true , то кубит в операции принимает состояние |1〉, иначе кубит принимает состояние |0〉. В операции используется 2 кубита, кубит msg кодируется и оба кубита передаются ранее написанной операции Teleport .

operation TeleportClassicalMessage (message : Bool) : Bool { using ((msg, target) = (Qubit(), Qubit())) { if (message) {

X(msg);

}

Teleport(msg, target);

return MResetZ(target) == One; }

}

Чтобы вызвать данную операцию в классической программе необходимо подключить библиотеку qsharp и ранее написанный namespace Teleportation. import qsharp from Teleportation import TeleportClassicalMessage r = TeleportClassicalMessage.simulate(message=True) print("Отправили True, Получили:", r)

r = TeleportClassicalMessage.simulate(message=False) print("Отправили False, Получили:", r)

Результат выполнения данной программы:

Отправили True, Получили: True

Отправили False, Получили: False

Q# на данном этапе разработки уже представляется мощным языком для квантового программирования. В нём представлены как классические типы данных, так и квантовые простейшие типы:

• -    Int;

• -    BigInt;

• -    Double;

• -    Bool;

• -    Qubit. Кубит можно только передать другой операции или проверить на идентичность. Сами действия над кубитами реализуются при помощи вызова операций на квантовом процессора или его симуляции ;

• -    Pauli. Используется для базовой операции вращения и для определения наблюдаемое измеряемой длины. Может принимать только четыре возможных значения : Paulil, PauliX, PauliY, PauliZ;

• -    Result. Представляет результат измерения кубита. Может принимать значения One и Zero;

• -    Range. Представляет последовательность целых чисел, обозначенную как start..step..stop. Т.е. в последовательность 1..3..10 входят числы 1, 4, 7, 10;

• -    String;

• -    Unit. Имеет только одно значение () и используется для в операциях для обозначения, что Q# функция ничего не возвращает.

Также в Q# могут использоваться различные массивы: Qubit[], Int[][], (Bool, Pauli)[][]. Элементы массива не могут быть изменены после создания массива. Для создания модифицированного массива могут использоваться операторы обновления и переопределения, и/или копирования и обновления. Ещё в Q# есть тип Tuple и пользовательские типы данных, которые можно объявить при помощи newtype.

В Q# есть квантовые подпрограммы, которые называются операции и классические подпрограммы - функции, которые могут содержать классический код, но без квантовых операций.

В стандартном пакете Q# реализованы следующие квантовые операции:

• -    Pauli (X, Y, Z);

• -    Hadamard (H);

• -    Phase gate S (п/4);

• -    Gate T (п/8);

• -   Gate R - применяет вращение вокруг заданной оси Паули ( или эквиваленты Rx, Ry, Rz);

• - RFrac - применяет вращение вокруг заданной оси Паули на угол, заданный в виде двоичной

дроби ;

• - CNOT;

• -    CCNOT (Toffoli);

• -    SWAP;

• -    Exp;

• -    Measure;

• -    M - сокращенная форма для Measure([PauliZ], [qubit]);

• -    MultiM;

Qiskit

Активно разрабатываемый IBM проект с открытым исходным кодом. Написан на Python и C++ для Python. Состоит из четырех частей:

• -   Terra - включает в себя набор инструментов для написания программ на уровне квантовых

цепей и импульсов, оптимизации для конкретного физического квантового процессора;

• -    Aer - включает в себя высокопроизводительную среду симулятора для программного стека Qiskit. Содержит симулятор для выполнения схем, скомпилированных в Terra, а также инструменты для реалистичного шумового моделирования ошибок, возникающих во время выполнения на реальных устройствах;

• -    Aqua - содержит библиотеку квантовых алгоритмов, на которых могут быть построены приложения для квантовых вычислений. Aqua разработан, чтобы быть расширяемым, поэтому в него легко можно добавлять квантовые алгоритмы. В настоящее время позволяет экспериментировать в области химии, искусственного интеллекта, оптимизации и финансовых приложениях;

• -    Ignis - основа для понимания и снижения шума в квантовых цепях и системах.

Для написания программы на Qiskit необходимо установить qiskit и подключить в программе: import numpy as np from qiskit import(

QuantumCircuit, execute,

Aer)

from qiskit.visualization import plot_histogram

Затем подключается необходимый симулятор из Aer. Всего есть 6 разных симуляторов:

• -    qasm_simulator

• -    qasm_simulator_py

• -    statevector_simulator

• -    statevector_simulator_py

• -    unitary_simulator

• -   clifford_simulator

  -

• simulator = Aer.get_backend('qasm_simulator')

Далее необходимо создать квантовую схему при помощи класса QuantumCircuit, который принимает 2 параметра - количество кубитов |0) и классических битов 0.

circuit = QuantumCircuit(2, 2)

Применение гейта Адамара на кубит с индексом 0 для суперпозиции:

circuit.h(0)

Результат выполнения: Количество 00 и 11: {'00': 503, '11': 497} и схема (см. рис 1)

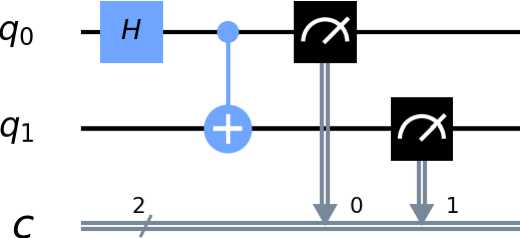
Рис. 1. Квантовая схема Qiskit

Для реализации на Qiskit квантовой телепортации введём секретное состояние, которое будет генерироваться применением серии унитарных гейтов на кубит в состоянии |0〉. Чтобы понять, что квантовая телепортация работает на выходе должно получиться тоже состояние, которое передано в начале. Qiskit позволяет не только выполнить симуляцию на компьютера пользователя, но и на квантовом компьютере IBM , в отличии от Q#, на котором пока можно пользоваться только симулятором. Но в этой работе Qiskit также рассматривается только в симуляции. Особенность запуска программы на квантовом компьютере заключается в том, что ошибки в гейтах приведут к тому, что небольшая доля результатов будет равна 1 (в случае, если мы всегда начинаем с |0〉 и должны получить 0). Подключение Qiskit: secret_unitary = 'hz'

import qiskit as qk from qiskit import ClassicalRegister, QuantumRegister, QuantumCircuit from qiskit import execute, Aer from qiskit import IBMQ

Для начала необходимо написать функцию, которая применяет ряд унитарных гейтов из заданной строки ( secret_unitary) : def apply_secret_unitary(secret_unitary, qubit, quantum_circuit, dagg er):

functionmap = {

'x':quantum_circuit.x,

'y':quantum_circuit.y,

'z':quantum_circuit.z,

[functionmap[unitary](qubit) for unitary in secret_unitary] else:

[func- tionmap[unitary](qubit) for unitary in secret_unitary[::-1]]

Далее необходимо создать квантовую схему с тремя кубитами и тремя битами. Первый кубит – который будет телепортироваться, про который объект, телепортирующий кубит, ничего не знает, второй кубит – находится у того же объекта, что и первый кубит, третий кубит – пункт назначения для телепортации. На первом шаге выполним ранее написанную функцию, создадим запутанность между вторым и третьим кубитом, сделаем телепортацию.

qc = QuantumCircuit(3, 3)

qc.barrier()

• #    Запутанность

qc.h(1)

qc.barrier()

• #    Телепортация

qc.h(0)

qc.measure(0, 0)

qc.measure(1, 1)

qc.barrier()

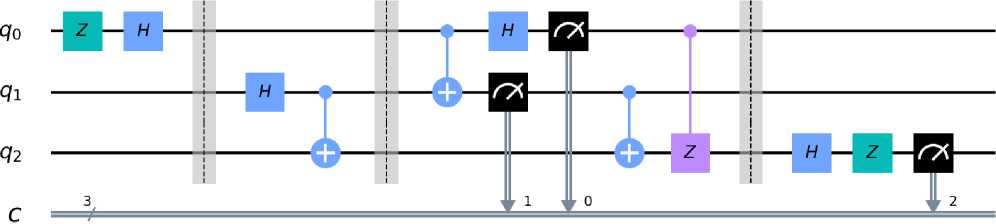
Рис. 2. Схема квантовой телепортации

Выполним симуляцию полученной схемы и выведем в консоль результат:

measurement_result = sim_result.get_counts(qc) print(measurement_result)

Результат выполнения: {'000': 236, '001': 266, '010': 261, '011': 261}.

Существуют и похожие на Qiskit проекты с открытым исходным кодом, использующие Python : Ocean от D-Wave, ProjectQ от Института теоретической физики в Швейцарской высшей технической школе Цюриха, Forest (pyQuil) от Rigetti Computing . Подробное сравнение Qiskit, Quantum Developer Kit, ProjectQ, pyQuil представлено в [7] .

Заключение

В данной вводной статье кратко рассмотрен один из первых квантовых языков программирования QCL. Большая часть статьи уделена современному квантовому языку программирования Q# и фреймворку Qiskit . В статье рассмотрено несколько не сложных с точки зрения реализации программ при помощи Q# и Qiskit : создание суперпозиции, квантовой запутанности, телепортация. Сам подход к написанию программы несколько схож: в Q# последовательно пишется операция, применение гейтов к кубитам, а затем запуск симуляции в классический программе на языке Python . В Qiskit создаётся квантовая схема, применяются различные гейты к кубитам схемы, а затем готовая схема запускается на симуляторе. По сравнению с Q# Qiskit более стабильный, в Qiskit больше сообщество, лучше документация и количество примеров, их качество. Наибольший вклад в открытый репозиторий Q# внесли 2 человека, а всего на данный момент в репозитории 34 участника. Однозначно, этим проектом занимается больше людей, данные только на основе информации из открытого репозитория [9]. В репозитории Qiskit-terra 18 участников можно назвать очень активными, а всего 136 участников [10] и это только число основного репозитория Qiskit . Также, на данном этапе только Qiskit предоставляет возможность выполнить симуляцию в облаке на квантовом оборудовании. Microsoft планирует запустить Azure Quantum , но в данный момент подобной возможности нет.

Поэтому на данный момент Qiskit наиболее подходящий и надёжный вариант для решения различных задач при помощи квантовых вычислений. Однако необходимо следить за развитием Q# , т.к. полноценное написание квантовых программ на классических языках программирования - это временный вариант, сам квантовый язык Q# гораздо перспективнее. Также в Quantum Developer Kit в ближайшем будущем может появиться больше возможностей, чем представляет Qiskit.