Квантовый генетический алгоритм: выбор типа и вида корреляции в квантовом нечетком выводе

В мире уже давно идут активные исследования в области квантовых вычислений. Появление реального квантового компьютера даст огромный скачок в различных областях, увеличит скорость работы множества алгоритмов. Однако, пока квантовый компьютер является больше гипотетическим устройством, и лишь некоторые явления квантовой физики удается по-настоящему использовать, исследователям остаётся применять квантовые явления на классическом компьютере.

Разработка квантовых алгоритмов – очень важная задача, т.к. чем больше появляется сфер применения квантовых компьютеров, тем больше финансов страны мира будут вкладывать в проведение исследований. В данной статье рассматривается применение квантовых поисковых алгоритмов в интеллектуальных системах управления (ИСУ), т.е. в системах, которые способны функционировать в непредвиденных ситуациях с гарантированным достижением цели управления (свойство робастности). При этом развиваются они уже не один десяток лет. Серьёзное развитие ИСУ за последние годы привело от зарождения самой идеи, до создания коллективов роботов, автомобилей с автопилотом и множества других систем, которые способны работать в нештатных и непредвиденных ситуациях [1]. В задачах управления поддержка свойства робастности функционирования сложного слабо структурированного объекта управления (ОУ) за счет применения ИСУ и технологий интеллектуальных вычислений необходима для достижения цели управления в условиях риска и непредвиденных (или нештатных) ситуаций управления. С алгоритмической точки зрения эффективное решение актуальной проблемы обеспечения устойчивого функционирования ОУ в условиях неопределенности и сохранения робастности ИСУ означает, что в используемом алгоритме достижения цели управления выполняются следующие необходимые и достаточные (в общем случае антагонистические) условия [1-3]: 1) минимум исходной информации о внешней среде (или возмущение, действующее на ОУ); 2) минимальный расход обобщенного полезного ресурса в ОУ и ИСУ.

Следовательно, разработка корректного алгоритма проектирования робастности ИСУ является одной из актуальных задач современной теории и систем управления; одновременно данная проблема относится к сложной и слабо исследованной области разработки ИСУ, способных эффективно и надежно функционировать в условиях риска и непредвиденных ситуаций управления [4-7].

В [1-3] разработана информационная технология (ИТ) проектирования робастных баз знаний (БЗ) на основе открытого в [8] синергетического эффекта их самоорганизации в непредвиденных ситуациях. Используемый в квантовом алгоритме принцип минимума информационной энтропии гарантирует необходимое условие самоорганизации – минимум требуемой исходной информации в сигналах обучения; термодинамический критерий минимума новой меры обобщенного производства энтропии обеспечивает достаточное условие самоорганизации – робастность процессов управления. В условиях риска и непредвиденных ситуациях оптимизация БЗ по информационнотермодинамическим критериям с помощью квантового алгоритма самоорганизации обеспечивает инвариантное достижение цели управления в реальном времени с требуемым уровнем робастности ИСУ. Примеры эффективного моделирования самоорганизации робастных БЗ в ИСУ динамически неустойчивым существенно нелинейным объектом в непредвиденных ситуациях показали эффективность разработанной ИТ.

Целью статьи является разработка ИТ проектирования робастных БЗ с применением квантовых эффектов самоорганизации [1, 8] в условиях непредвиденных ситуаций управления и риска. Результат разработки заключается в обеспечении гарантированного достижения цели управления в непредвиденных (нештатных) ситуациях управления в реальном времени, как следствие применения квантового генетического алгоритма (КГА) управления в структуре самоорганизующейся ИСУ.

В настоящей публикации (выступающей продолжением [1, 8]) описываются принципы построения, структура и практическое применение разработанной ИТ проектирования робастных БЗ в ИСУ, 2

эффективно и надежно функционирующих в условиях риска и непредвиденных ситуаций управления на основе модели самоорганизации БЗ, разработанной в [1, 2].

Основной задачей разработанного КГА является поиск оптимальных видов и типов корреляций между классическими состояниями коэффициентов усиления ПИД-регуляторов в соответствии с физической интерпретацией слабоструктурированной модели ОУ и извлечения скрытой в классических состояниях коэффициентов усиления квантовой информации, которая является дополнительным информационным ресурсом для формирования робастных БЗ с применением квантового нечеткого вывода. Приведен пример эффективного моделирования самоорганизации робастных БЗ в ИСУ динамически неустойчивым существенно-нелинейным ОУ.

Интеллектуальные системы управления

Развитие ИТ проектирования ИСУ основанное на применении мягких вычисления, обычно используют методологии нечеткой логики, эволюционных алгоритмов и нейронных сетей. Базисом развития систем управления послужили PID -регуляторы, которые зачастую, не справляются с задачей управления и плохо работают в непредвиденных ситуациях. Нечеткие регуляторы, позволяют частично расширить сферу применения ПИД регуляторов, за счет добавления правил функционирования и частично адаптировать систему. Использование генетических алгоритмов и нечёткой нейронной сети позволило полностью адаптировать систему, но для обучения такой системы требуются временные затраты, что в нештатных и непредвиденных ситуациях является критическим критерием. Моделирования оптимального сигнала позволяет создать частичную самоорганизацию в системе за счет обнаружения оптимальных траекторий коэффициентов усиления ПИД-регулятора. Применение квантовых вычислений и, как частного примера квантовым нечётким выводом, позволяет повысить робастность без затрат временного ресурса – в режиме реального времени. На рис. 1 показана интеллектуальная система управления с объединением нескольких нечётких регуляторов и КНВ, которая позволяет создать новое качество в управлении – самоорганизация в режиме online.

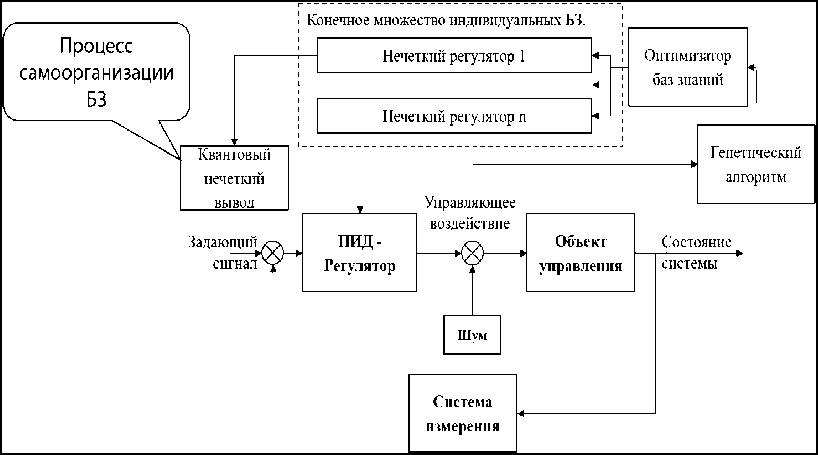
Рис. 1. Интеллектуальная система управления с квантовым нечетким выводом

Квантовый нечёткий вывод

Главная проблема интеллектуальных систем управления заключается в том, что очень трудно спроектировать глобально хорошую и робастную структуру управления на все возможные случаи. Особенно, когда система работает в слабо предсказуемых ситуациях. Одно из лучших решений – формирование конечного числа баз знаний нечеткого регулятора для множества фиксированных ситуаций управления. Цель квантового регулятора объединить базы знаний, полученные при помощи оптимизатора баз знаний в самоорганизующиеся квантовые нечеткие регуляторы. Квантовый нечет- кий вывод использует частные индивидуальные базы знаний нечеткого регулятора, каждая из которых получена с помощью инструментария оптимизатора баз знаний.

Процесс проектирования квантовой алгоритмической ячейки включает матричную форму трех квантовых операторов: суперпозиции, запутанности и интерференции, которые являются частью структуры квантовых поисковых алгоритмов. В общем виде структура квантовой алгоритмической ячейка (QAG) с применением квантового генетического алгоритма (QGA) описана в (1) в виде:

QAG = [ ( Int ® ⁿ I ) • U_F ] h ^{+ 1} • [ QGA ] [ ⁿ H ® ^m S ] , (1) где I - тождественный матричный оператор; символ ® обозначает тензорное произведение; S равен I или H в зависимости от описания проблемы. Первая часть в проектировании уравнения (1) – это выбор типа оператора запутанного состояния U , который физически описывает качественные свойства функции.

Основным блоком такой интеллектуальной системы управления, является квантовый генетический поисковый алгоритм (КГПА, QGSA – quantum genetic search algorithm ) (см. рис. 2).

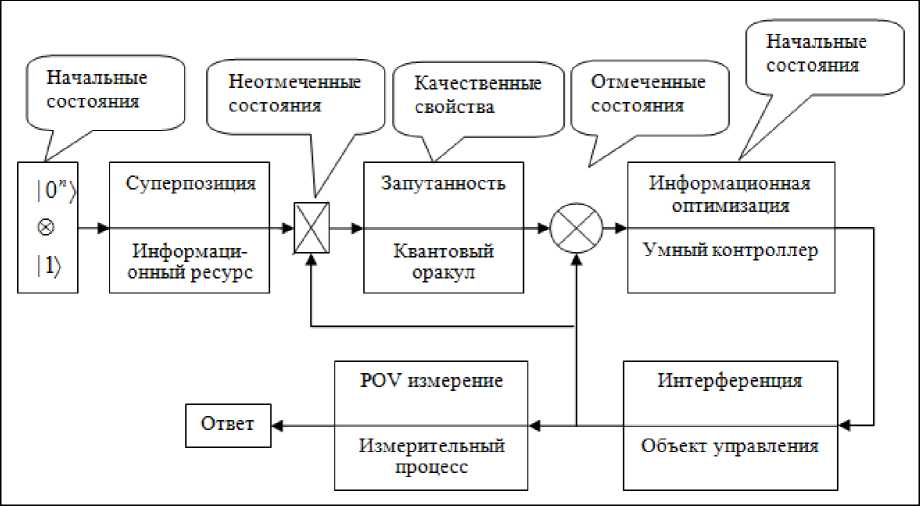
Рис. 2. Самоорганизующийся интеллектуальный квантовый поисковый алгоритм для интеллектуальной системы управления

Основные элементы структуры квантового поискового алгоритма (КПА, QSA – quantum search algorithm ), как главного блока глобальной оптимизации, основанной на квантовых мягких вычислениях, представлены на рис. 3.

Формально структуру КГПА описывается следующим множеством логических операторов:

QGSA = ( C,Ev,P0,L,[Q,х,mV ,[Sup,Ent,Inth ,M, GA - операторы QA - операторы где C – алфавит для генетического кодирования индивидуума для конкретной задачи; Ev – функция пригодности; P0 - начальная популяция; L - размер популяции; Q - оператор отбора (селекции); X - оператор скрещивания; ц - оператор мутации; Sup - квантовый оператор линейной суперпозиции; Ent – квантовый оператор запутывания (смешанное состояние); Inf – оператор вывода; Д - условие остановки, включающие такие критерии остановки, как оптимум заданной функции пригодности и минимум энтропии Шеннона/фон Неймана. Структура на рис. 2 – базовая модель интеллектуальной системы управления, описывает набор логических операторов КГПА. Комбинации логических операторов КГПА могут быть другими и отличатся от представленной формы, представляя различные варианты КПА.

На рис. 3 представлена квантовая алгоритмическая ячейка ( QAG ) квантового нечеткого вывода. Такая ячейка может быть реализована как на классическом, так и на квантовом процессоре, а также может быть интегрирована в различные системы управления и встроенные интеллектуальные контроллеры.

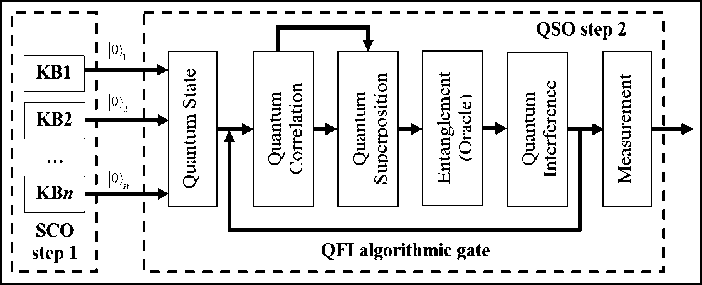
Рис. 3. Квантовая алгоритмическая ячейка (QAG) квантового нечеткого вывода

Алгоритм квантового нечеткого вывода для определения новых коэффициентов усиления ПИД-регулятора K (см. рис. 4), состоит из таких этапов, как нормализация, формирование квантового бита, после которого осуществляется подбор оптимальной структуры квантовой алгоритмической ячейки, выбирается состояние с максимальной амплитудой, осуществляется декодирование и на выходе получаем новый параметр k [7, 8].

На входе квантовый нечеткий вывод получает коэффициенты от сформированных заранее баз знаний нечеткого регулятора [7] на основе оптимизатора БЗ на мягких вычислениях.

Следующим шагов осуществляется нормализация полученных сигналов [0, 1] путем деления текущих значений сигналов управления на их максимальные значения ( max k ), которые заранее известны.

Формирование квантовых битов . Определяются функции плотности распределения вероятностей. Они интегрируются и из них получаются функции распределения вероятностей. Они позволяют определить виртуальные состояния сигналов управления для формирования суперпозиции с помощью преобразования Адамара из текущего состояния введённых сигналов управления. Используется закон вероятности: p (| 0 ) ) + (|1 ) ) = 1 , где p (| 0 ) ) - вероятность текущего реального состояния, а p (| 1 ) ) - вероятность текущего виртуального состояния. По текущему реальному состоянию из закона сохранения вероятностей определяется виртуальное состояние.

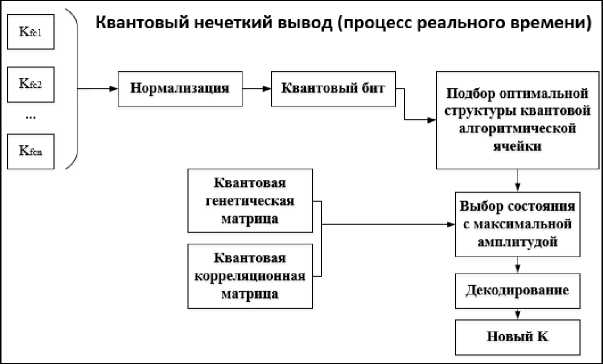
Рис. 4. Алгоритм квантового нечеткого вывода

Суперпозиция квантовой системы « реальное состояние – виртуальное состояние » имеет вид:

I V > = ^( V p (|0»*|0 >+V (1 - p (|0 > ) *|1 > ) .

На рис. 5 показан процесс формирования квантовых бит для текущего реального состояния нормированного сигнала управления, описывающего коэффициенты усиления нечеткого ПИД-регулятора.

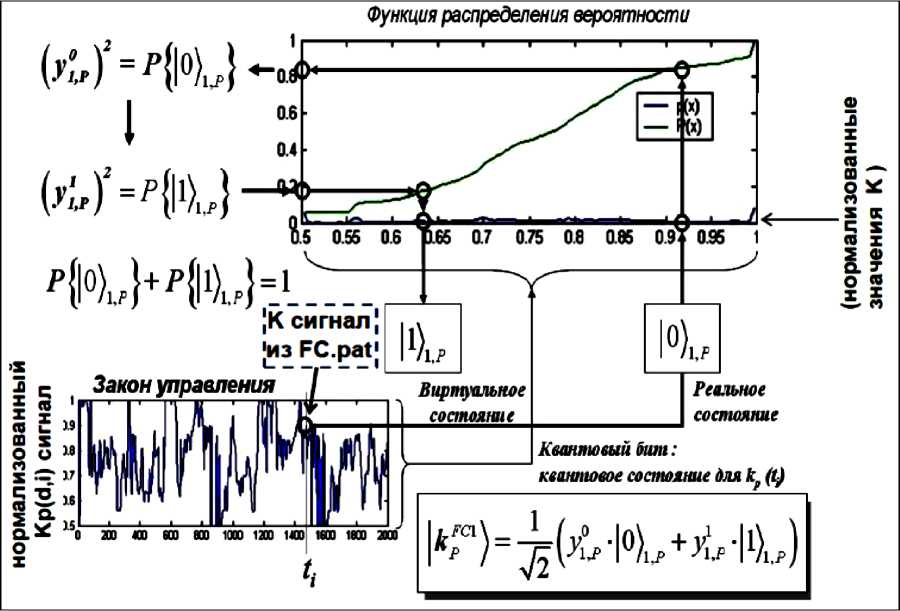
Рис. 5. Формирование суперпозиций состояний

На следующем этапе происходит выбор типа квантовой корреляции – операция построения запутанных состояний. Рассматривается 3 типа квантовой корреляции: пространственная, временная и пространственно-временная. Каждая из них содержит скрытую в спроектированных баз знаний ценную квантовую информацию [8].

Квантовая корреляция и роль скрытой в классических состояниях квантовой информации

Квантовая корреляция рассматривается как физический вычислительный ресурс, позволяющий увеличить успешный поиск решений алгоритмически неразрешимых проблем. В нашем случае решение задачи обеспечения глобальной робастности функционирования ОУ в условиях непредвиденных ситуаций управления за счет проектирования оптимальной структуры и законов изменения коэффициентов усиления ПИД-регулятора классическими методами управления является алгоритмически неразрешимой проблемой [1-9]. Решение данной проблемы возможно на основе технологий квантовых мягких вычислений [8, 13]. Выходные параметры ПИД-регуляторов рассматриваются как активные информационно взаимодействующие агенты, из которых формируется результирующая управляющая сила ОУ (см. ниже рис. 7 и 8). В многоагентной системе существует новый синергетический эффект, возникающий при обмене информацией и знаниями между активными агентами ( swarm synergetic information effect ) [7-9].

За счет синергетического эффекта создается дополнительный информационный ресурс и многоагентная система (с учетом множества баз знаний), способна решать сложные динамические задачи по выполнению совместной работы. Поставленная задача может не выполняться каждым элементом (агентом или базой знаний) системы в отдельности в разнообразных средах без внешнего управления, контроля или координации, но обмен знаниями и информацией позволяет совершать совместную полезную работу коэффициентам усиления ПИД-регуляторов для достижения поставленной цели управления в условиях неопределенности исходной информации и ограничений на расход полезного ресурса [10,11].

В частности, известно, что для систем управления с обратной связью, количество извлекаемой t полезной работы W удовлетворяет неравенству Waх (t) = kJ T^Icdt’ ^ kTIc, где к — постоянная Больцмана на, TVn (t) интерпретируется как наименьшая достижимая температура системой во времени t при управлении с обратной связью, предполагая T^п (0) = T, и Ic определяет количество информации Шеннона (перенос энтропии), извлекаемое системой из процесса измерения [10-12].

Физически синергетический эффект означает самоорганизацию знаний и создание дополнительного количества информации, которая позволяет совершить многоагентной системе полезную работу с минимумом потери полезного ресурса и при минимуме требуемой исходной информации, без разрушения нижнего исполнительного уровня системы управления [8, 13]. Совместно с информационно-термодинамическим законом интеллектуального управления (оптимальное распределение качеств управления «устойчивость – управляемость – робастность») проектируется ИСУ многоагентными системами, гарантирующая достижение цели управления в условиях неопределенности исходной информации и ограниченного полезного ресурса [8, 11, 12].

Разработанная модель самоорганизации и используемые результаты

В [1, 13] задача проектирования свойства робастности (как самостоятельного свойства самоорганизации) ИСУ подробно изучена на основе новых видов интеллектуальных вычислений, таких, как мягкие и квантовые вычисления. Предложена модель КА самоорганизации ИСУ, базирующаяся на принципах минимума информационной энтропии (в “интеллектуальном” состоянии сигналов управления) и обобщенной термодинамической мере производства энтропии (в системе “объект управления + регулятор”). Основным результатом применения процесса самоорганизации является приобретение необходимого уровня робастности и свойства гибкости (адаптивности) воспроизводимой структуры. Отмечено, что свойство робастности (по своей физической природе) выступает в качестве составной части самоорганизации, а требуемый уровень робастности ИСУ достигается за счет выполнения принципа минимума производства обобщенной энтропии.

Принцип минимума производства энтропии в ОУ и системе управления [1] является физическим принципом оптимального функционирования с минимальным расходом полезной работы и лежит в основе разработки робастной ИСУ. Данное утверждение базируется на том, что для общего случая управления динамическими объектами оптимальное решение конечной вариационной проблемы определения максимума полезной работы W эквивалентно, согласно [14], решению конечной вариационной проблемы нахождения минимума производства энтропии S .

Таким образом, исследование условия максимума функционала max(W ) (где q, u – обобщен-qi ,u ные координаты ОУ и сигнал управления соответственно) эквивалентно, согласно [12,14], исследованию ассоциированной проблемы минимума производства энтропии, т. е. min(S) . Следовательно, в qi ,u разработанной модели КА используемый принцип минимума информационной энтропии гарантирует необходимое условие самоорганизации – минимум требуемой исходной информации в сигналах обучения; термодинамический критерий минимума новой меры обобщенного производства энтропии обеспечивает достаточное условие самоорганизации – робастность процессов управления с минимальным расходом полезного ресурса.

Извлечение скрытой квантовой информации

Основная идея состоит в следующем: используя сигналы управления с первого и второго нечетких регуляторов, (см. рис. 1) строятся новые выходные значения коэффициентов усиления (вектора управления) в соответствии с выбранным типом корреляции.

Процесс оптимального извлечения ценной квантовой информации из классических состояний базируется на следующих четырёх фактах в квантовой теории информации:

• 1.    существует эффективный квантовый алгоритм сжатия данных;

• 2.    в квантовом состоянии присутствует «сцепленное» представление классической и квантовой информации;

• 3.    полная корреляция в квантовом состоянии представляет собой «смесь» классической и квантовой корреляций;

• 4.    присутствует скрытая (частично доступная извлечению) классическая корреляция в квантовом состоянии.

Каждая из корреляций характеризует связь между соответствующими сигналами управления обоих нечетких регуляторов или баз знаний.

Для подсчёта новых k_p , k_l , k_D пространственной корреляции применяются следующие формулы (1 и 2 индексы нечеткого регулятора):

{ k * ( t ) k p ( t ) k D ( t ) k D ( t )} - для k p ;

{ k ^ (t ) k^t ) k \ (t ) k /( t )} - для k , ;

{ k^x_t(t ) k ²( t ) k^x_p(t ) kp(t )} - для k_D .

Для подсчёта новых k_p , k_l , k_D временной корреляции применяются следующие формулы (1 и 2 индексы нечеткого регулятора):

{ k P ( t ) k P ( t -A t ) kp( t ) kp( t -A t )} - для k_p ;

{ k ^ ( t ) k ^ ( t -A t ) k D ( t ) k D ( t -A t )} - для k I ;

{ k p ( t ) k p ( t -A t ) k ²( t ) k /( t -A t )} - для k_D .

Для подсчёта новых k_p , k_l , k_D пространственно-временной корреляции применяются следующие формулы (1 и 2 индексы нечеткого регулятора):

{ k P ( t ) k 1 ( t -A t ) kp( t -A t ) kp( t )} - для k_F ;

{ kP ( t ) k 1 ( t - A t ) k2_D ( t - A t ) k ² ( t )} - для k ;

{ k p ( t ) k P ( t -A t ) k ²( t -A t ) k p{ t )} - для k_D .

Для вычисления k пространственной корреляции используется алгоритм формирования суперпозиции запутанных состояний (см. рис. 6 и рис. 7).

Рис. 6. Выбор приоритетного квантового состояния

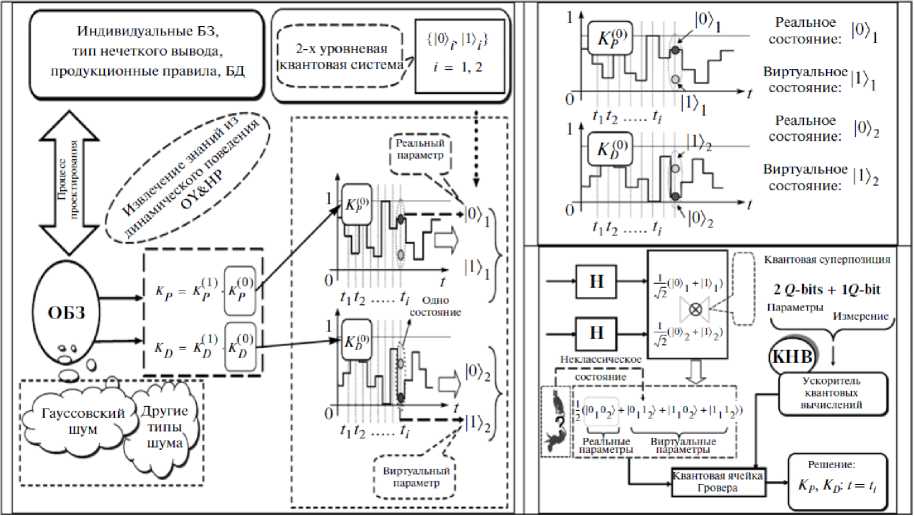
Рис. 7. Формирование и выбор компонент суперпозиции из различных сигналов управления и состояний (реальных и виртуальных)

Рассмотрим, например, согласно рис. 8, следующий тип квантовой корреляции: { k 1 (t ), k 1 (t ), k 2 ( t ), k 2 ( t )} ^ k"™(_t ) , где индексы 1 и 2 указывают принадлежность к соответствующим БЗ. Тогда квантовое состояние | a_xa₂a₃a₄ ) = | k 1 ( t ) k 1 ( t ) k2(t ) k 2 ( t ) ) рассматривается как коррелированное ( entangled ) состояние.

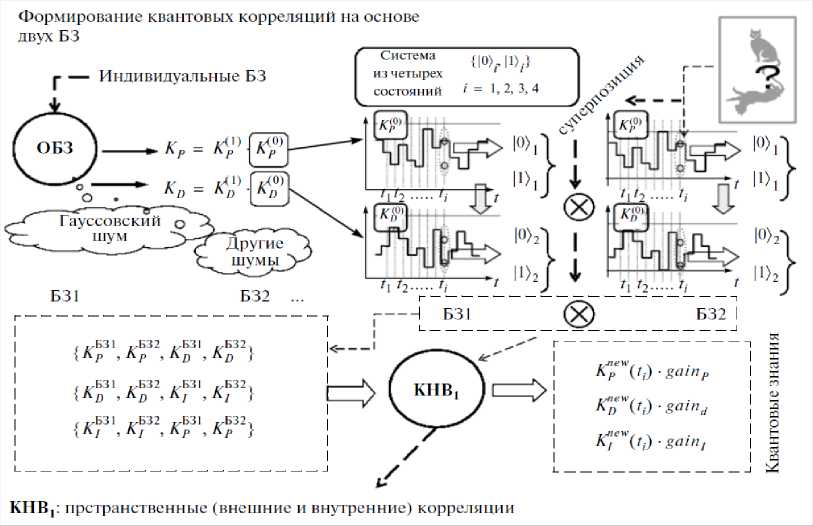
Рис. 8. Процесс формирования квантовой корреляции (пространственной, внешней и внутренней) между сигналами управления коэффициентами усиления Kp и Kd от двух БЗ

Графический интерфейс пользователя для формирования квантовых состояний в суперпозиции и их кодирование для выбранного типа квантовой корреляции показан на рис. 9.

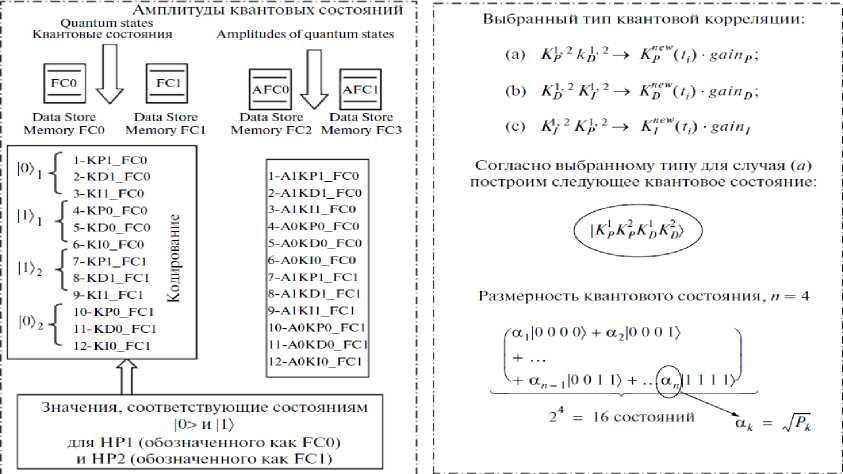
Рис. 9. Графический интерфейс пользователя формирования квантовых состояний в суперпозиции и их кодирование

Рисунок 10 содержит алгоритм вычисления пространственной корреляции (см. рис. 8) и процесс формирования «интеллектуального» состояния. На этом же рис. 10 показаны внутренняя и внешняя корреляции между сигналами управления коэффициентами усиления двух различных БЗ.

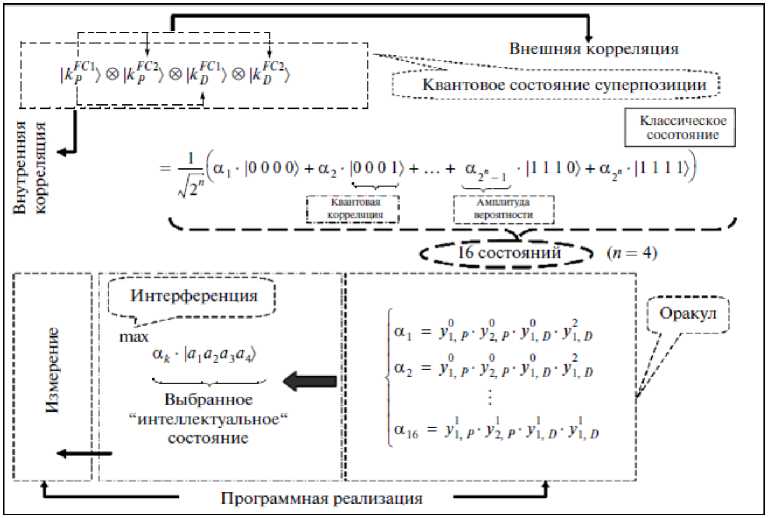
Рис. 10. Алгоритм вычисления пространственной корреляции и процесс формирования «интеллектуального» состояния

Графический интерфейс пользователя для формирования и вычисления «интеллектуального» квантового состояния по принципу максимума амплитуды вероятностей отражен на рис. 11.

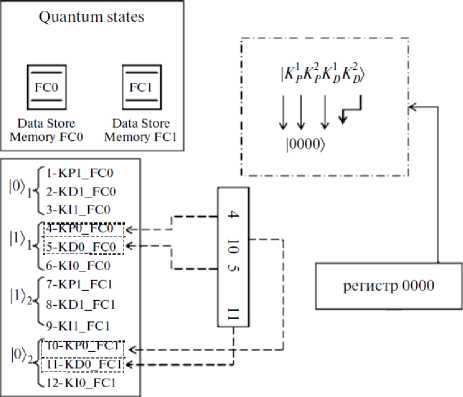
Выбрать состояние 0000 из данных

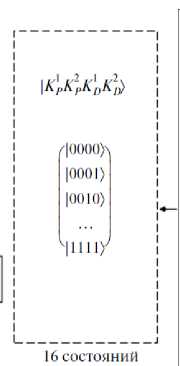
Результат: регистр |4 10 5 111 используется для выбора амплитуды состояния 0000 из данных

Рис. 11. Графический интерфейс пользователя для формирования и вычисления «интеллектуального» квантового состояния по принципу максимума амплитуды вероятностей

Алгоритм вычисления амплитуды вероятностей квантового состояния и его реализация в среде MatLab / Simulink представлены на рис. 12.

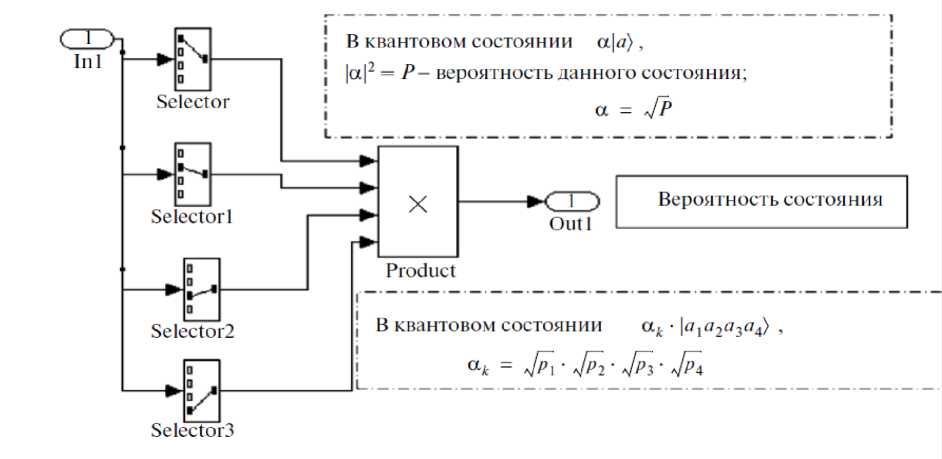
Рис. 12. Алгоритм вычисления амплитуды вероятностей квантового состояния и его реализация в среде MatLab/Simulink

Пример результатов работы блока измерений квантовых состояний с максимальной амплитудой вероятностей для трех коэффициентов усиления приведен на рис. 13.

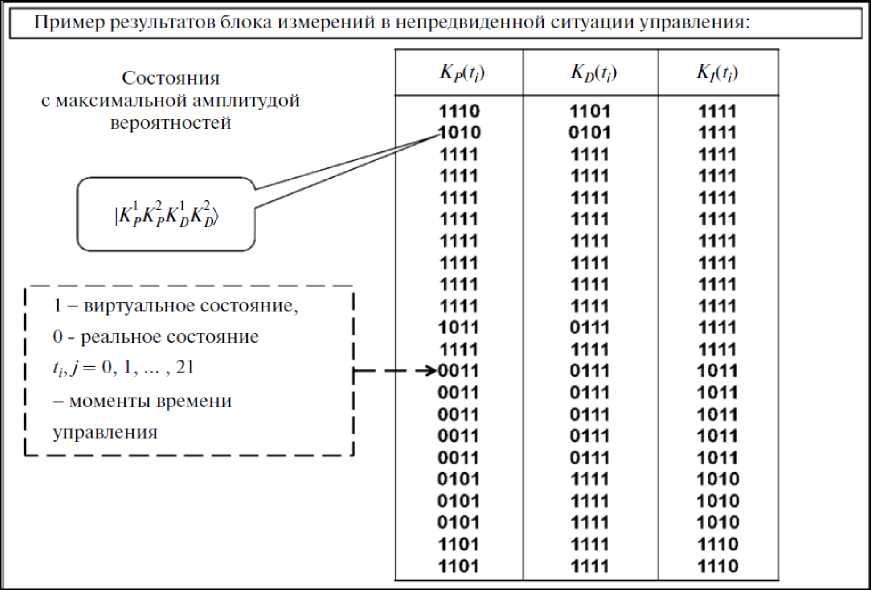
Рис. 13. Пример результатов блока измерений квантовых состояний с максимальной амплитудой вероятностей для трех коэффициентов усиления

В результате применения КНВ в структуре ИСУ осуществляется извлечение дополнительной (скрытой) квантовой информации, а ее использование дает возможность проектировать робастные сигналы управления в реальном времени из реакций НР на непредвиденные ситуации управления.

Отметим, что на рис. 10, показано, как новое состояние k строится из суперпозиции состояний:

|kPFC1〉⊗|kPFC2〉⊗|kDFC1〉⊗|kDFC2〉, которые присутствуют в выбранном запутанном состоянии. | kFc 1) и представляет из себя квантовое состояние из суперпозиции реального и виртуального состояний текущего kFC 1, и описывается сле дующим образом: | kFC 1) = —,= (уг0р | 0), уУхр |1), р) , применяя тензорное произведение между пре-V 2     ,         ,     ,        ■ образованиями Адамара, в результате получается суперпозиция выбранных состояний (комбинации коэффициентов усиления). В предыдущем примере имеется 16 состояний.

Автоматизация выбора типа квантовой корреляции проводится при помощи квантового генетического алгоритма, выбор которого будет произведён в следующем разделе.

Виды и операторы квантовых генетических алгоритмов

Существует несколько различных видов квантовых генетических алгоритмов. Все они построены на комбинации квантовых и классических вычислений. Квантовые вычисления включают в себя квантово-генетические операторы, выполняющие генетические операции на квантовых хромосомах. Эти операторы называют interference gates (интерференционные ворота).

Существует несколько операторов обновления, но наиболее востребованным является Q-gate интерференции (вращения) [19]. Оператор квантовой интерференции обозначается как gate U ( t ) :

' cos(30_j )   - sin( 50j )

^ sin( 50 _y)    cos(50j ) ,

Применяя этот оператор, эволюция популяции есть результат процесса унитарных преобразований. В особенности, вращения ( rotations ), приближающие состояние хромосом к состоянию оптимальной хромосомы в популяции.

В классическом ГА оператор выбора имитирует дарвиновский естественный отбор, улучшая популяции, продвигая особи с лучшей пригодностью и наказывая тех, кто имеет худшую производительность. В КГА выбор заменяется изменением всех особей на лучшую. Поэтому, когда популяция обновляется оператором вращения, популяция сходится, но обычно КГА попадает в локальные опти-мумы, которые подвергаются преждевременной конвергенции (сходимости). Чтобы избежать этого КГА часто включают в себя либо рулетку, либо элитный выбор. Например, КГА с шагом выбора используется в улучшенном алгоритме кластеризации К-средних. Существуют ещё более экстремальные подходы, например, когда КГА включает в себя выбор и алгоритм имитации отжига, исключающий преждевременную конвергенцию. В других случаях шаг выбора включается, не прибегая к операторам, обычно используемым в ГА. Такой случай полуклассического ГА, где оператор селекции (выбора) стремится к максимальной пригодности посредством квантового подхода, например, используя алгоритм Гровера [15].

Оператор квантовой мутации (инверсия). В имитации ГА существует также квантовая версия классического оператора мутации. Гейт выполняет межкубитную мутацию j-го кубита, заменяя амплитуды квантовый гейтом Паули.

Оператор квантовой мутации (ввод). Этот гейт напоминает биологический механизм введения хромосом. Вставка хромосомы означает, что сегмент хромосомы был вставлен в необычную позицию на той же или другой хромосоме. Квантовая версия этого генетического механизма включает перестановку или обмен между двумя случайно выбранными кубитами (левый, правый). Например, предположим, что, учитывая следующую хромосомы, выбирается случайным образом первый и третий кубиты.

Оператор квантового перехода (классический). Квантовый кроссовер моделируется похоже на классический алгоритм рекомбинации, используемый в ГА, но работает с амплитудами вероятности. И хотя квантовая версия мутации может быть реализована на квантовом компьютере, есть теоретиче- ские причины, препятствующие сделать кроссовер. Тем не менее, несмотря на теоретические ограничения, квантовая версия классического оператора кроссовера применяется во многих практических задачах оптимизации. В этих случаях поиск решения осуществляется с использованием квантового эволюционного «вдохновляющего» подхода. Вслед за этим оператор иллюстрируется для случая одноточечного кроссовера. В этом примере, если точка разреза произвольно выбирается, например, точка между первым и вторым положениями, тогда происходит обмен хромосомными сегментами.

Оператор квантового перехода (интерференция). Настоящий квантовый оператор выполняет кроссовер путем рекомбинации в соответствии с критерием, основанным на рисовании диагоналей. В результате все особи смешиваются друг с другом, приводя к потомству.

Классификация квантовых эволюционных алгоритмов

Выделены два основным класса квантовых эволюционных алгоритмов: квантовый генетический алгоритм (КГА) и гибридный генетические алгоритмы (ГГА).

Схема КГА включает в себя следующие шаги:

• 1.    Инициализация квантовой популяции Q (0)

• 2.    Создаём P (0) , показатель каждого отдельного Q (0) ^ P (0)

• 3.    Вычисляем P (0) - классическое вычисление

• 4.    While (не состояние окончания) do

• 5.    Begin

• 6.    t —— t + 1

• 7.   Q-gate вращения

• 8.   Q-gate мутации

• 9.    Делаем оценку Q (0) ^ P (0)

• 10.    Вычисляем P(t) – классическое вычисление

• 11.    Завершение.

Схема ГГА включает в себя следующие шаги:

• 1.    Инициализация квантовой популяции Q (0)

• 2.    Создаём P (0) , показатель каждого отдельного Q (0) ^ P (0)

• 3.    Вычисляем P (0) - классическое вычисление

• 4.    While (не состояние окончания) do

• 5.    Begin

• 6.    t —— t + 1

• 7.    Q-gate вращения

• 8.    Оператор кроссовер

• 9.    Q-gate мутации

• 10.    Делаем оценку Q (0) ^ P (0)

  
  
  
  

Вычисляем P ( t ) - классическое вычисление

Завершение.

Оба квантовых алгоритма были протестированы на примере применения их в задаче нахождения корней уравнения f (x) =| x — — + sin(x) |.

Результаты моделирования

КГА в результате выполнения поставленной задачи показывает следующее (см. рис. 14).

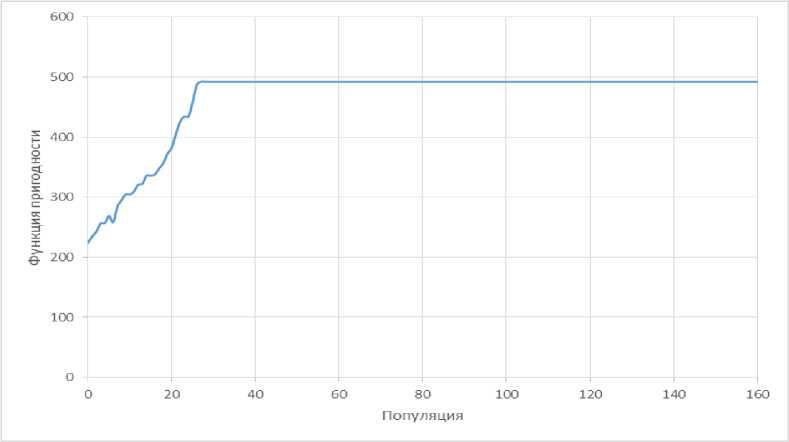
Рис. 14. Результат выполнения КГА

Видно, что после примерно 30 популяции значение функции пригодности перестаёт меняться. ГГА показывает следующие результаты (см. рис. 15).

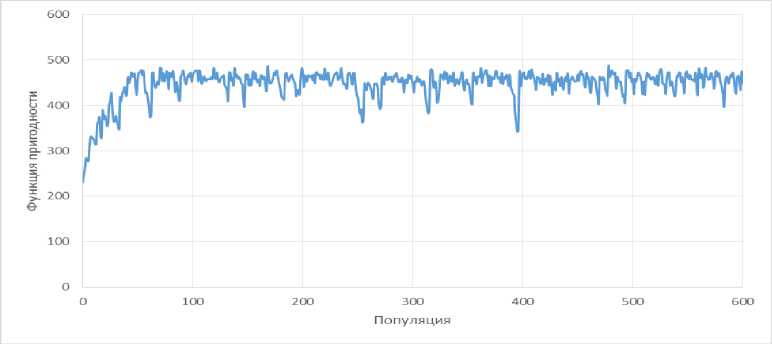
Рис. 15. Результат выполнения ГГА

КГА и ГГА алгоритмы можно рассматривать как классические методы оптимизации, основанные на принципах квантовых вычислений. Программы, реализующие такие методы, могут выполняться на цифровом компьютере, что подразумевает практические или теоретические трудности.

Примечание . В настоящее время одной из проблем в квантовом искусственном интеллекте является разработка истинных квантовых эволюционных алгоритмов и, следовательно, программ, которые в будущем могут работать на квантовом компьютере. Однако некоторые проблем возникают, когда происходит перевод классического ГА в квантовую версию. Это даже можно назвать парадоксом, т.к. ГА имеет сходство с квантовым алгоритмом Гровера: ГА – это параллельные методы поиска, хотя в обычных приложениях эта функция не реализована. Одной из основных проблем с алгоритмами КГА и ГГА является поиск метода для измерения популяции особей, но без разрушения состояния суперпозиции хромосом. Кроме того, что на сегодняшний день ключевой вопрос заключается в том, как реализовать в квантовом компьютере оператор кроссовера. В то время, как мутация может быть легко проведена в квантовом компьютере с использованием гейта Паули, не ясно как выполнять кроссовер, используя для этого квантовомеханические явления.

Одна из интересных идей была предложена в 2004 году [16], сделав первые шаги в реализации генетического алгоритма на квантовом компьютере [8]. Автором предложен настоящий квантовый эволюционный алгоритм, который можно назвать сокращенным квантовым генетическим алгоритмом (СКГА).

Алгоритм состоит из следующих этапов:

• 1.  Инициализация суперпозиции всех возможных хромосом;

• 2.  Оценка пригодности оператором F;

• 3.  Применить алгоритм Гровера;

• 4.  Квантовый оракул;

• 5.  Применение диффузионного оператора Гровера G;

• 6.  Сделать оценку.

Написав программу поиска решений уравнения для СКГА для той же задачи, что и КГА с ГГА результат выполнения стала матрица (см. рис. 16). Поиск решений выполняется за одну операцию. Результатом является матрица, где наибольшее значение имеет искомое решение (число 11).

[[0.078125] [0.078125] [0.078125] [0.078125] [0.078125] [0.078125] [0.078125] [0.078125] [0.078125] [0.078125] [0.078125] [0.953125] [0.078125] [0.078125] [0.078125] [0.078125]]

Рис. 16. Результат выполнения алгоритма СКГА

В КГА и ГГА эволюция является результатом унитарных преобразований, особенно вращений, приближающих состояние хромосом к состоянию оптимальной хромосомы с максимальной пригодностью. Поскольку эта процедура повторяется поколение за поколением, то результатом является быстрая сходимость к локальным оптимумам, имеющим место локальной ловушки.

Общая стратегия улучшения качества КГА заключается в использовании небольших усовершенствований алгоритма. Например, включая новые операторы, например, квантовое бедствие, возмущение или другие настроенные алгоритмы [17]. Но во многих случаях эти операторы полезны только в высокоспецифичных приложениях [18,19].

Можно сделать вывод, что эволюция (оптимизация) квантовых эволюционных алгоритмов является результатом вращения квантового гейта, который вводит явление интерференции. Таким образом, особи корректируются или модифицируются, чтобы быть более похожими на лучшую особь в популяции. Получается, что популяция подвергается более низкому дарвиновскому давлению отбора. Однако в ГА после оценки особей алгоритм, имитирующий выбор (например, оператор выбора родителей) заменит старую популяцию P ( t ) на новую популяцию P ( t +1) особей. Поскольку особи выбираются в соответствии с их значением пригодности, то популяция решений развивается через дарвиновскую эволюцию, но с большим давлением отбора, чем КГА и ГГА. Следовательно, ГА заменяет устаревшие стратегии инновационными стратегиями, представленными потомством. Аналогично, когда кроссовер включен как шаг в алгоритме ГГА его производительность обычно становится ближе к ГА.

Преимущество квантовых генетических алгоритмов в том, что они требуют меньше хромосом, чем ГА. В теории, в истинном квантовом генетическим алгоритм (СКГА) можно считать, что популяция составлена из одной хромосомы в состоянии суперпозиции [16]. Этот факт может быть странным, но не с точки зрения квантовой механики. Более того, алгоритм СКГА демонстрирует, что с использованием квантовых вычислений стратегия генетического поиска становится ненужной. Эволюция происходит в одном поколении.

Анализ и сравнение результатов моделирования системы «движущаяся каретка – перевернутый маятник»

Проведя исследования с различными типам корреляции было определено, что наилучший результат показывает пространственно-временная корреляция, обнаруженная ручным методом в [7, 8].

Запустив написанный квантовый генетический алгоритм на несколько тысяч поколений (см. рис. 17), можно увидеть, что около 70% на лучшие показатели у пространственно-временной корреляции. Q-S-T - пространственно-временная корреляция, Q-T - временная, Q-S - пространственная.

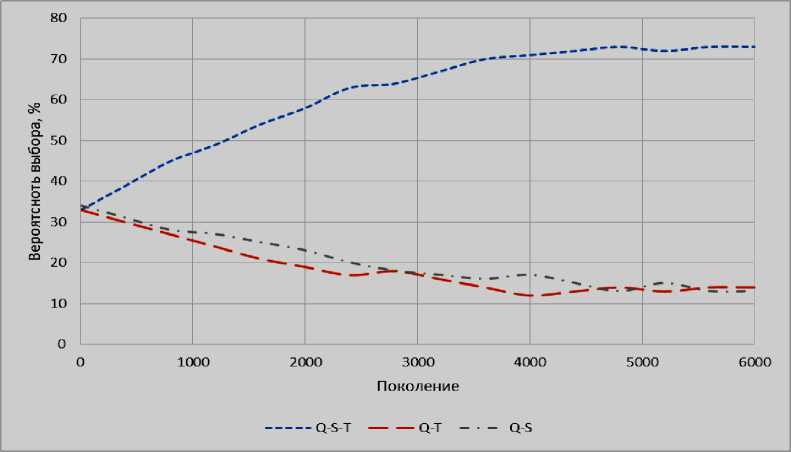
Рис. 17. Результат выполнения квантового генетического алгоритма

Временная и пространственная корреляции имеют примерно одинаковый процент. Стоит отметить, что после 5000 поколений в данном случае изменение вероятностей уже не происходит.

Запустив квантовый генетический алгоритм 200 раз можно заметить, что вероятность выбора пространственной-временной корреляции опустилась до 60% (см. рис. 18).

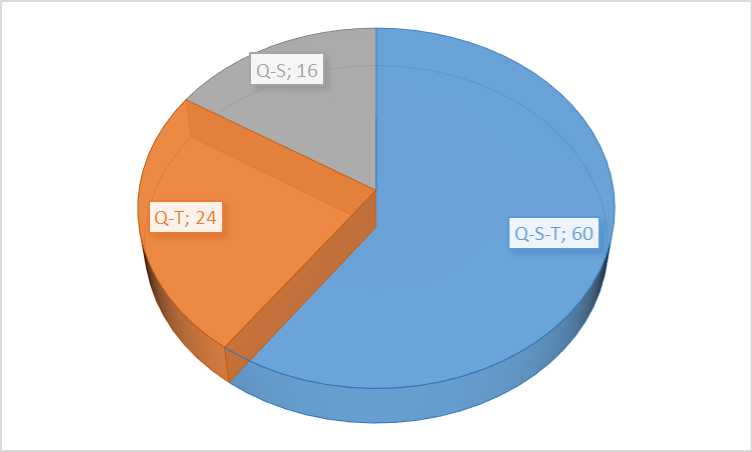
Рис. 18. Результат выполнения квантового генетического алгоритма 200 раз

После этого шага было смоделировано поведение различных алгоритмов на примере системы «движущаяся каретка-перевёрнутый маятник» (см. рис. 19).

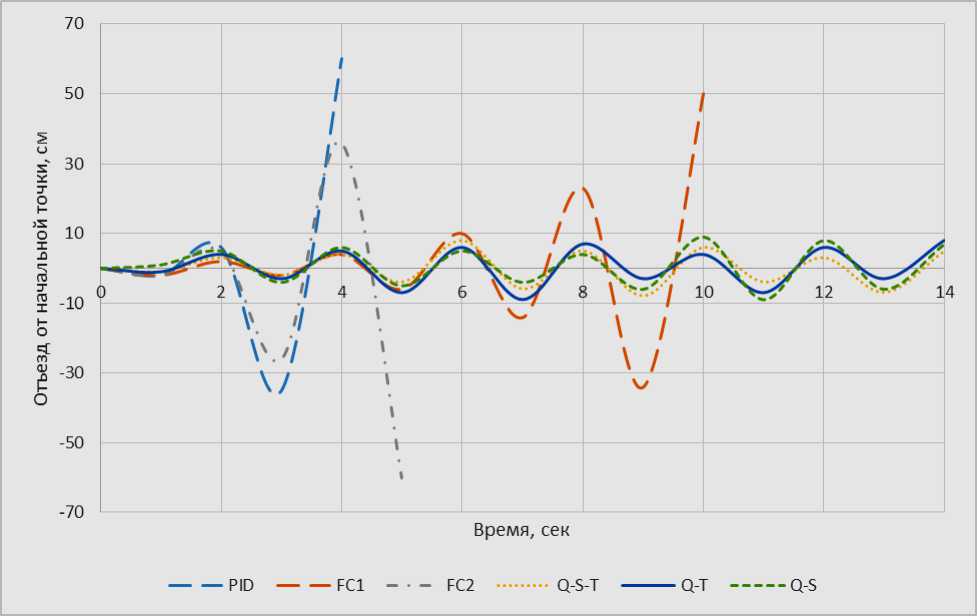
Рис. 19. Сравнение поведения различных алгоритмов

Как видно на графике, PID -регулятор и нечёткий регулятор не справляются с заданной задачей из-за появления непредвиденной ситуации. Все 3 квантовые алгоритмы справились с ситуацией, а пространственно-временная корреляция показала наилучшие результаты.

Заключение

В данной статье кратко описана история развития интеллектуальных систем управления. Основное внимание уделено использованию квантового нечёткого вывода и выбора типа корреляции. Автоматизация выбора оптимального типа квантовой корреляции влияет на улучшение робастности системы. Показан способ нахождения оптимального типа квантовой корреляции – при помощи квантового генетического алгоритма. Проведено сравнение 3-х квантовых генетических алгоритмов и особое внимание уделено сокращённому квантовому генетическому алгоритму с использованием алгоритма Гровера и квантового оракула. Подобный алгоритм позволяет проводить отбор в одном поколении. Однако применение его на классическом компьютере возможно только в простых задачах, а на большом количестве возможных решений алгоритм сейчас слабо эффективен. Выбранный квантовый генетический алгоритм был разработан для поиска оптимального типа квантовой корреляции и проведен анализ его работы на примере системы «каретка-перевёрнутый маятник», где тип корреляции, выбранный квантовым генетическим алгоритмом, совпал с типом корреляции, показывающий лучшие результаты при ручном выборе.