Кватаронный механизм формирования структурных единиц опало- подобных материалов

Сорок лет назад было сделано сенсационное открытие [1]. Оказалось, что благородный опал состоит из закономерно расположенных сферических частиц кремнезема, размеры которых в диаметре составляют 150 ÷ 450 нм (рис. 1). В последующем было установлено, что эти частицы, в свою очередь, сложены еще более мелкими, но также сферическими частицами [2]. Подобное глобулярное внутреннее строение часто обнаруживается для многих других природных аморфных веществ и коллоидных частиц. Однако механизм образо-вaния монодисперсных сферических частиц, слагающих опалоподобные материалы до сих пор остается неясным. В данной работе в рамках кватаронной концепции генезиса наночастиц предлагается общий принцип построения аморфных частиц типа опаловых структурных единиц.

Главная идея кватаронной концепции [3, 4] заключается в том, что в пересыщенных растворах образуются и могут существовать специфические нанокластеры — кватароны. Пересыщение раствора ln(c/c0) и радиус ква-таронов r связаны следующим выражением [3]:

Ш^ = ^ с0 RTr

V-XZeJ 16л²НТ88₀Г⁴

, (1)

где с и с₀ — реальная и равновесная концентрации раствора, V_m — мольный объем, γ ₀ — удельная поверхностная

Рис. 1. Монодисперсные сферические частицы кремнезема в искусственном опaле

энергия, R — универсальная газовая постоянная, T — температура, Ze — заряд, ε ₀ — электрическая постоянная, ε — относительная диэлектрическая проницаемость, параметр δ примерно равен диаметру кластерообразующих атомов или структурных единиц. Выражение (1) представляет собой модифицированный, с учетом заряда и зависимости поверхностной энергии от радиуса частицы, вариант известной формулы Гиббса—Томсона. Последняя получается из выражения (1) при (Ze) = 0 и r → 0.

Для электронейтральных частиц зависимость (1) графически представлена на рис. 2. Согласно выражению (1), даже в условиях нулевого пересыщения в растворе существуют частицы (кластеры) определенного разме-рa (r ≈ δ ). Такие кластеры невозможны в рамках классической теории зародышеобразования. Они были названы ква-таронами [3].

Фундаментальное значение для формиро-ʙaния аморфных коллоидных частиц имеет то обстоятельство, что потенциальными центрами кристаллизации являются только кватароны, рa-диус которых ≥ 4δ. Квата-роны меньших размеров представляют собой аморфные “квазижид-кие” или “квазитвердые” образования сферической формы. При достаточно большой концентрации кватароны могут агрегироваться. Eсли это происходит, то механизм образования аморфных коллоидных частиц может быть очень простым: в пересыщенном растворе образуются и существуют аморфные наноразмерные кластеры, которые при определенных условиях агрегируются и формируют аморфные же частицы более крупных размеров.

В принципе образование относительно крупных частиц ʜa основе ква-таронов может происходить в результате: 1) плотной их упаковки, 2) слияния, 3) фрактальной агрегации.

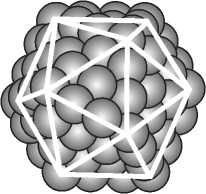
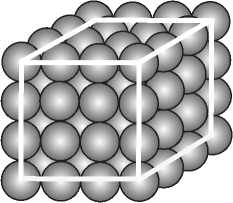
Плотная упаковка кватаронов ведет к формированию упорядоченных ГЦК- и ГПУ- структур (надмолекулярных кристаллов) (рис. 3, a) типа тех, что формируют фуллерены углерода в конденсированном состоянии (фуллери-тов), что, естественно, исключает образование аморфных сферических частиц. Возможна ситуация, когда квата-роны в результате плотной упаковки формируют близкие к сфере икосаэд-рические частицы (рис. 3, б). Такие частицы и дальше могут увеличивать-

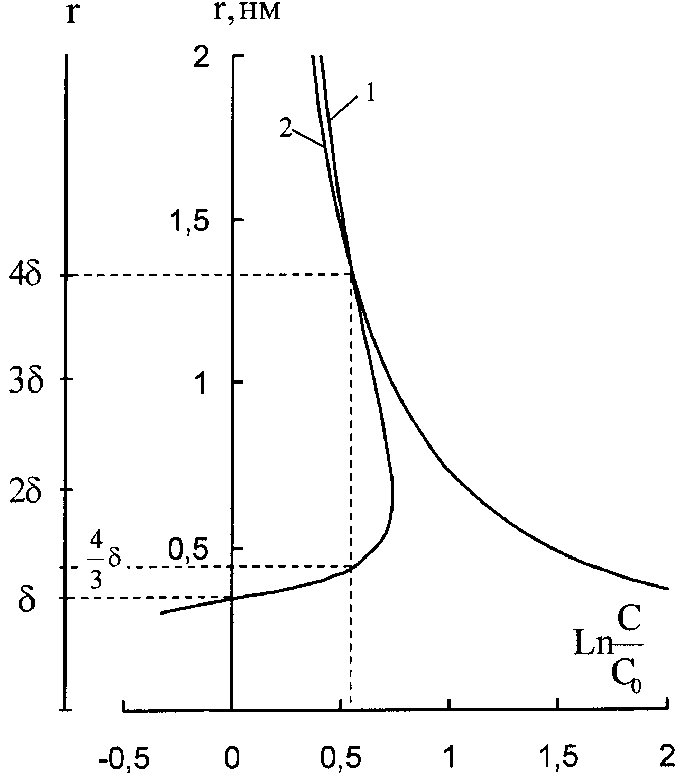
Рис. 2. Зависимость радиуса равновесных кватаронов SiO₂ от пересыщения раствора. Кривая 1 построена по урaвне-нию (1) при (Ze) = 0, V_m = 22.69 см³/ᴦ∙моль, γ ₀ = 66.7 эрг/см², δ = 0.33 ⋅ 10^‒7 см, Т = 350 °К. Кривая 2 построена по формуле Гиббса—Томсона при тех же параметрах, кроме γ = 3/4 γ ₀ = = 50 эрг/см²

няется, из соотношений (4) и (5) находим:

и

б

а

Рис. 3. Плотная упаковка “квазитвердых” кватаронов с в пределах от 2 δ до 4 δ _. Чем формированием кристаллических (а) и некристаллических меньше радиус кватаро_-^{(б) частиц}                    нов, тем их требуется

ся в своих размерах путем последовательного наращивания наружных оболочек. Однако подобные икосаэд-рические частицы среди структурных единиц опалоподобных материалов практически не встречаются. Хотя отдельные аморфные частицы таким способом и могут сформироваться. Пример подобных объектов описан в работе [5], где икосаэдрическая частица образована кластерами В12 в суб-оксиде бора.

Квазижидкий характер кватаронов делает в принципе возможным их слияние, с образованием однородного вторичного кластера более крупного размера. Слияние происходит, когда суммарная поверхностная энергия N объединяющихся кватаронов радиусом r больше или равна поверхностной энергии образующегося кластера радиусом R:

,      (2)

где γ(r0) и γ(R) — удельные поверхност- ные энергии первичных кватаронов и вторичного большого кластера.

Зависимость удельной поверхностной энергии от радиуса частицы имеет вид [6, 7]:

,            (3)

где γ ₀ — удельная поверхностная энергия для плоской границы раздела. Тогда из выражения (2) получим:

.

р u

крупной частицы

Предполагая, что плот- Рис. 4. Слияние “квазижидких” кватаронов с формированием более

Из условия сохранения массы в процессе слияния кватаронов следует, что:

где ρ0 и ρ — плотности квата-ронов и образующейся час тицы.

ность при слиянии не изме-

. (6)

Следовательно, размеры кватаронов, способных к слиянию, находятся больше для слияния. Так, при слиянии 8 кватаронов радиусом r0 = 3δ образуется новый кластер (частица) радиусом R = 6δ (рис. 4). Слияние же кватаронов радиусом r0 = 2.5δ становится возможным при N = 64. При этом образуется частица радиусом R = 10δ. Согласно формулам (6), в результате слияния кватаронов всегда об- разуются вторичные частицы, радиус которых r > 4δ. Судьба таких частиц, как указывалось выше, предопределена — они с высокой вероятностью будут кристаллизоваться. Следовательно, роль слияния кватаронов в формировании аморфных структурных единиц опалоподобных материалов незначительна.

При фрактальной агрегации сохраняется индивидуальность агрегирующихся кватаронов и вместо (5) выполняется условие

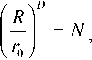
где N — число кватаронов в сфере радиусом R, полученном в результате агрегации кватаронов радиусом r0, D — фрактальная размерность.

Отличительной особенностью фрактальных агрегатов является непрерывное уменьшение плотности по мере увеличения их размеров. Действительно, из сравнения формул (5) и (7) следует, что

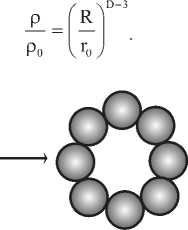
Поскольку D < 3, то с увеличением радиуса R плотность ρ уменьшается.

После логарифмирования выражения (8) легко получается формула, связывающая радиус фрактального кластера с радиусом агрегирующихся ква-таронов:

.         (9)

3-D

Из приведенных выше формул можно получить также и выражения для определения фрактальной размерности кластеров:

1п^

и                    . (10)

In— InN —In— Г                   Ро

Согласно этим формулам, D зависит от N и ρ/ρ₀ (рис. 5). Величина ρ/ρ₀ для кластера максимальна, когда вся его поверхность покрыта кватаронами, и минимальна, когда к кластеру прилипает лишь один кватарон. К примеру, при агрегации кватаронов радиусом r₀ = δ, в первом случае имеем ρ/ρ₀ = 0.89, а во втором — ρ/ρ₀ = 0.333. Соответственно число атомов N в сфере радиусом R = 3/2 δ в первом случае составит 24, а во втором — 9. Тогда фрактальные размерности, согласно формулам (10), равны 2.89 и 2.0. Среднее значение D составляет 2.445, что совпадает с характерным для DLA-модели формирования фрактального кластера значением, равным 2.46 ± 0.05 [8].

Далее, полагая что D ≈ 2.5 и ρ/ρ₀ = 0.37 (до этого значения в свободно-дисперсной системе сохраняется целостность агрегата [9]), из формулы (10) получим формулу для определения радиуса вторичных частиц:

lnR = lnr0 + 2.         (11)

Сформировавшиеся таким образом вторичные частицы могут по той же схеме построить агрегаты следующего иерархического уровня и т. д. Соответственно для радиуса частицы n-го уровня имеем:

lnRn = lnRn-1 + 2. (12)

Ниже (см. таблицу) приводятся результаты модельных расчетов значений радиусов фрактальных кластеров, полученных в предположении агрегации кватаро-нов различных размеров. В расчетах величина δ полагается равной 0.3 нм (диаметр

кватаронобразующих структурных единиц или молекул).

Согласно приведенным в таблице данным, характерные размеры структурных единиц опалоподобных материалов гарантированно достигаются на 3-м уровне фрактальной агрегации кватаронов даже при наименьших размерах первичных кватаронов (r = δ ). В некоторых случаях (при r₀ > 2 δ ) это происходит уже на 2-м уровне.

Как отмечалось выше, радиусы первичных частиц (ква-таронов), фрактальная агрегация которых возможна, находятся в интервале от δ до 2 δ или близки к 4 δ . Фрактальная

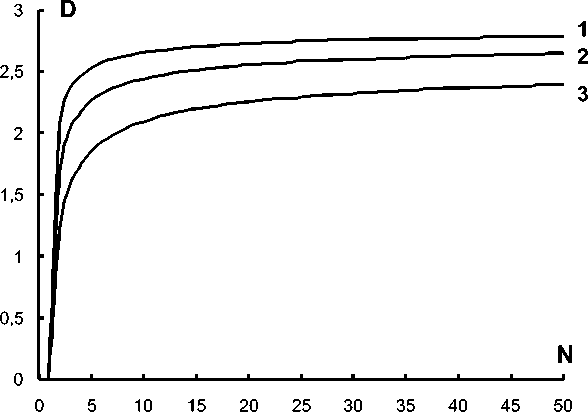
Рис. 5. Зависимость фрактальной размерности D от числа частиц N при ρ/ρ₀ = 0.74 (1), ρ/ρ₀ = 0.59 (2), ρ/ρ₀ = 0.37 (3)

на ситуация, когда свободное пространство между агрегирующимися кластерами данного иерархического уровня заполняется кластерами предыдущего уровня или первичными кватаронами. Тогда мы будем иметь дело с фрактальными агрегатами, находящимися внутри матрицы. Такой механизм образования аморфных частиц сферической формы не имеет внутренних размер

агрегация же кватаронов радиусом от 2 δ до 4 δ может происходить, если это квазитвердые объекты с заполненными внутренними оболочками, способные сохранять свою индивидуальность при агрегации. Частицы радиусом r > 4 δ формируют аморфные структуры при условии, если они по какой-либо причине не могут кристаллизоваться. К примеру, это имеет место, когда они представляют собой объекты некристаллографической симметрии (икосаэдрические кластеры).

Кватароны имеют радиус 2 δ при пересыщениях, близких к предельным (максимум на кривой 1 на рис. 2). Однако реально получить и поддерживать такие пересыщения из-за возможных эффектов гелеобразования чрезвычайно трудно. Выпадение кристаллической фазы из раствора начинается при меньших пересыщениях (пунктирная линия на рис. 2), когда радиус кватаронов достигает значений 4 δ . Поэтому наиболее вероятные размеры исходных кватаронов, формирующих фрактальные кластеры, по-види-мому, находятся вблизи 4/3 δ . Это со-

Радиусы фрактальных кластеров разного иерархического уровня

Радиусы г0 первичных частиц

5	2.2
4/35	3.0
25	4.4
35	6.7
45	8.9
65	13.3

гласуется также с тем, что соответствующий радиус частицы первого иерархического уровня агрегации (~ 3 нм) весьма близок к тому, что получается на основе различных оценок и экспериментальных наблюдений. В частности, примерно такого размера частицы предполагаются первичными при формировании коллоидных частиц кремнезема [10].

Предложенная модель образования аморфных наночастиц объясняет ряд труднообъяснимых фактов. Так, установленная в экспериментах по синтезу монодисперсных сферических частиц кремнезема дискретность в их размерах [11] связана как с разными иерархическими уровнями агрегации частиц кластеров, так и с различиями в размерах исходных кватаронов. Частое присутствие кристаллической фазы в опалоподобных материалах является следствием участия в формировании составляющих их структурных единиц кватаронов с близкими к 4 δ радиусами, которые кристаллизуются.

В заключение отметим, что в процессе фрактальной агрегации возмож-

Радиусы кластеров разного уровня, в нм

1-й уровень

2-й уровень	3-й уровень
16.3	120.4
21.8	161.4
32.8	242.1
49.1	363.1
65.5	434.1
98.3	726.2

ных ограничений. В результате могут формироваться достаточно крупные макроскопические частицы. Но эти частицы не имеют прямого отношения к генезису опалоподобных материалов, хотя и представляют очевидный минералогический интерес.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (проект № 02-05-64688) и Программы фундаментальных исследований Президиума Российской академии наук.