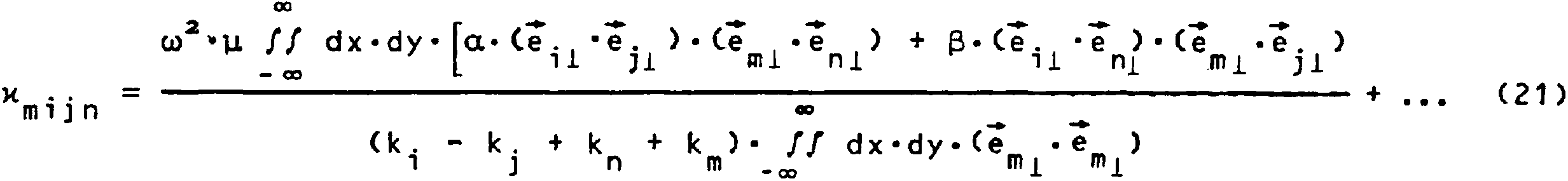Квазидинамическое моделирование нелинейной эволюции импульсов в нерегулярных многомодовых градиентных волноводах

При этом

* -      _ I 1 для к = к

П • е = 6     = (n m

(ба)

nm   т n  1л

0 для к F к

I            п т

Подставляя теперь (5) и (2) и опуская громоздкие выкладки, с учетом (6а)

имеем:

э2р

____m

9z2

ОО

Е к = 0

-к

— (kJ к !

(к)

3kF

9tk

Л                                          3A '

П •A + i-ECO -e' )•(П • —- mi        m Ml m 3

При этом, как нетрудно показать, в линейном регулярном случае (когда А = 0)

решение (?) сводится к эволюционным уравнениям для медленных амплитуд:

D f m m

О,

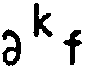
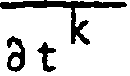
(8)

----21 + к . ----21 + ------21 . ------21--21 . -------- - . . .

dz m at 2 at2 6 at3

При A # О эволюционные уравнения содержат возмущающие факторы Rm:

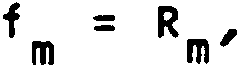
определение которых и составляет конечную цель данной работы.

Конкретизируя А, примем, что при соТ » 1 (Т - характерная длительность им пульса) влияние возмущающих факторов сказывается во втором порядке теории дис-

1Р(нел)|     1 2

персии, то есть IYI— ^------ ~ (—)• Тогда масштабы затухания и самовоздействия соизме- е I?! фТ                                                     _ римы с длиной дисперсионного расплывания импульса. При этом структура А± распадается в (3) на нерегулярную и нелинейную части вплоть до членов ~ (^) , что позволяет принять в (9) Rm = R^^ + КтНвЛ)’ кР°ме того, можно показать, что необходимая для вычисления Допредельная компонента поля Ez соответствует в первом приближении квазидинамической структуре (5):

Ez

Е (F е _ n nz п

i •

3F п 1 . т—- • е ) 3 t nz

Определяя в рамках изложенного влияние нерегулярности, будем учитывать взаимосвязь соседних мод, ограниченных разросом волновых чисел "к < к < 3-к m n m

Тогда во втором дисперсионном приближении

получим

где

_r(y) = m

-E

n

Г mn

п

1 (к -к )-z n m

е

mn

п m

;(v> n

/(к  + km^

n m

-(Y) n

= 0)2ЦЕ¥ *

е ni

1<еп ‘ W

Конкретизируем дели [1]:

влияние нелинейности в

рамках безынерционной кубической мо-

Р

• Е + 3-(Е-Е)-Е*

При

этом, подставляя, согласно (5), (10),

Е(0>

Е п

е е^, имеем п п

где

где

*(нел)

г^п =

D(нел) m

Н . .     = m 1 j п

Е F.F.F ijn 1 1 п

е*) • е^ J п

(3), (7) в

Е i «и

С1 jn

* 3-(е.•е )•е* .

1 n j том же приближении получим

п

i•(к .-к.+к

1 J

п

-к

m1-z

(17)

П -а(“ел>/(к.

m 1 j n i

J

к п

к m

*(нел) а . .

1 j п

_    . .       div с /1  + i(k.-k.+k)*cJ

²   -1jп . -           1               1 j n 2

= О) Ц ‘ С ,       + VI -----------------------------------------------------

(здесь так же, как и в (11), (12)

разброс волновых чисел соседних мод огра

ничен -к < к . - к. + к < 3 • к ) .

m 1 j n          m

Следует отметить, что найденные общие выражения (12) и

(18) для матриц

Г их.. резко упрощаются в "толстых" многомодовых волноводах, когда m n       m i j п оо2це • г2 » 1. При этом в (6) можно проигнорировать наличие продольных модовых компонент, а в (13) и (19) удалить члены ,W1 .

Тогда

00                   нер)              ——

// dx-dy• (u)2u*Ae 4     /1 + wuo) • (е *e )

ml nl

Г =--- +, . .

mn                     ”_

(k + k ) • ff dx-dy-(e -e ) n m _mi mi

Однако при исследовании "тонких" маломодовых волноводов (когда to2]ie • г2 ^ 1) и учете продольного поля отброшенные слагаемые могут конкурировать с основными и становиться определяющими.

Полученные соотношения (8), (9), (11), (17) позволяют описать эволюцию модовых амплитуд fm и определить, согласно (5), (10), поля Е^ и Ez, замыкая тем самым решение поставленной задачи.

Приложение

При исследовании эволюции коротких импульсов возникает, как известно, ряд особенностей (например, асимметрия фронтов) члены третьего приближения теории дисперсии ответственность за которые несут ~ (~Т)3 [2,8]. Построенная квазиди-

вид этих слагаемых, а именно: к

намическая теория позволяет определить явный Су )

выражению (11) следует добавить AR^ :

где

к

AR (у) m

Г i n

Г mn

df

at

n

i ( k -k ) • z n m

e

mn

(k + k ) n m

(rv^1)-;?'

M n

\Ck + k ) x n m

выражению

(17)- ДР<нел): m

ДЯ(нел) = E m i J n

i и . .

m 1 j n

df .

at

f: • f

J n

и1 . . -f .

m i j n i

f + n

+ и

n

m i j n

где

(к.+k ) -и ..    + П

I m m i j n m

m 1 j n

s^ijn’^ ‘ (=ijn

(к. - к . + к + к ) i j n m

Здесь при вычислении лишь коэффициенты (с*5а*зл)

а.. подразумевается, что 1 j п и (1/е), а при вычислении

в (19) a^l)

цируются к^ и е^ (последние, согласно (16), определяет с

задается индексом I: для I = i, I = п имеем (+); для L =

по ш дифференцируются поив (19> дифферен-jn). Знак перед a^V^ j имеем (-) .