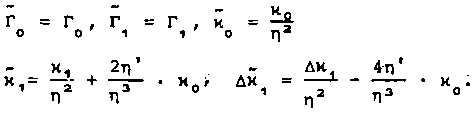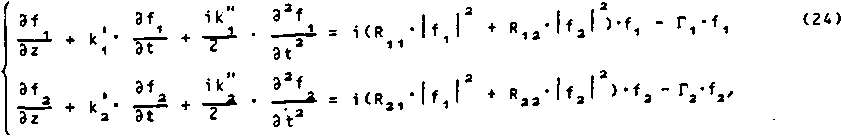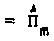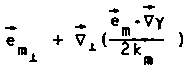Квазидинамическое моделирование нелинейной эволюции коротких импульсов

о°

Ниже используются нормированные ТЕ -моды, для которых on

ООу

/ 2nR • dR • е • е =6  , т.е. в (6) const = ---- . В частности, для угло- тф пф тп ,^—__ вых компонент ТЕ01 и ТЕ02 мод имеем e ■ --- exp(- —x—)z e = —— • C2 - v-R )-exp(- —y—) z(8)

причем в случае слабонаправляющего волновода ( △ « 1) можно положить:

п

«

CD VyT- Е

max

Для описания эволюции модовых амплитуд введем квазидинамическое разложение по модам поперечной составляющей электрического поля

ОО К

= Е 1т n К = 0 R1

d n -(K)         -

—5— • e_ = L(F -e л .            n ।              n n at a n

3Fn at

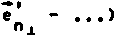
Здесь и далее Fn - fп (t,z)•exp(iknz), где - слабо зависящие от (t,z) комп-

-(К) _ Э е -I Эе лексные амплитуды, е = —, е ■    . Соотношение (9) является прямым елед-

Эш стеием аддитивного разложения Фурье-компонент поля по ортогональному набору поперечных модовых векторов Еп = ЕС _(z)‘e  (П,г.). При этом будем учитывать

U1       nW      П1 А

П             А лишь дискретный спектр к^, опуская вытекающие моды.

Следует отметить, что в отличие от случая стационарной монохроматической волны поперечная структура импульса каждой моды эволюционирует согласно (9) уже в первом приближении теории дисперсии. Данное обстоятельство игнорируется во многих работах (см. например, [б-9]). Между тем последовательное развитие пред- лагаемой теории указывает на то, что фиксация поперечного распределения модовых импульсов, т.е. использование вместо (9) разложения Т. = Е F (t,z) • е (г.), п п          п± приводит к физически необоснованным эффектам (например, ко взаимовлиянию импульсов различных мод в линейном регулярном волноводе). Учитывая важность данного утверждения, продемонстрируем его обоснованность на простейшем, легко проверяемом примере. Пусть ТЕ-моды планарного волновода (Е^ = Ez = О, Е^ = E(t,z,x)e ltot) распространяются в линейной, неоднородной, диспергирующей среде: ц = const, е = Ещ(х). Тогда волновое уравнение для медленной амплитуды примет вид

(~ + — > Е + w2We Е ♦ i (с^це) ' •                . З^Е + ... = о         (9.1)

3z2 Эх2                           co            2 9t =

Нулевое приближение (9.1) (—- + —- + 2ue)-E = 0 с учетом граничных усло-Зх

3z аий дает спектр волновых чисел km и

Е = е (со,х) • exp (i k z) , причем m m ' r m

З3е

----51 + (<о2ц-е (x) - к2)е = 0.

_9ха          со      mm

Если теперь ввести традиционное

модовых векторов ет(ы,х)

(9.2)

(но неверное !) разложение амплитуды Е(t,z,x)

по модам

Е = Е f (t,z)-e (о,х)•ехр(ik z),                                                  (9.3)

mm   m

m то в первом дисперсионном приближении из (9-1) имеем

(9.4)

модовых функций J dx •e_mⁱe_n = О При этом неоднородность е_щ(х)

при уг

Используя вытекающую из (9-2) ортогональность при m # п, домножим (9.4) на еп и проинтегрируем, по х не позволяет ортогонализировать коэффициенты

Э<п 9fm ^km-kn)z . ^^^1^^^ о.         (9.5)

2 к ■ _      + £ "к е                                              о п 3z т at                         /dx-e2

Таким образом, распространение мод в модели (9-1-9-3) не независимо даже в первом дисперсионном приближении, что не позволяет, например, ввести понятие групповой скорости отдельной моды. Скрытая причина подобного абсурда - некор- ректность традиционного разложения (9.3), т.е. недопустимость фиксации поперечного распределения моды в импульсе. Действительно, каждая гармоника импульса имеет свой профиль: ет зависит от w, причем, как показано ниже на конкретных примерах, эта зависимость отнюдь не мала.

Возвращаясь к общей теории, подставим (9) в (2). Тогда, ограничиваясь описанием вперед-бегущих волн (kffl > 0), можно получить эволюционные уравнения для медленных амплитуд fm(t,z) в виде

D m

= R m m

где левая часть определяется

D m

df ~ iK f = З-5 ~ 1 E FT m dz ^_^ KI

дифференциальным оператором dtK

dz m dt ♦ 2

а правая часть Rm связана с наличием возмущающих факторов, описанных согласно (3) вектором А.

Интересно отметить, что временную часть дифференциального оператора (11)

можно перевести в интегральную форму, полезную при анализе ряда задач

D-f(t,z) = т— 1- /dr • f(t*T)"S (т),                                    (11.1)

dz _ е                   со где ядро 5ш(т) суммирует информацию обо всех степенях дисперсионного разложения волнового вектора

V^t) = Н Л ^dD -е⁴⁰’⁰”^ . (k_n-k_M).                         (11.2)

Определяя структуру R^, учтем модовый характер возмущающих факторов. Это позволяет выделить в А медленные амплитуды, положив i q • z = Е А • е п .                                                                         (12)

п П1

В классе задач, требующих условия фазового синхронизма, можно принять qn = kn> В более общем случае qn определяется комбинациями волновых векторов. Используя (12), ограничимся первыми производными от медленных амплитуд А . Тогда при п 1 условии qn > - kn, опуская громоздкие преобразования, получим

• 1    (q -к )•z

Rm = Е Фшп " е ° m /                                                        (12.1)

где

Ф пп ~                 m "п

Дальнейшее развитие теории для конкретизации Rm (12) с помощью А (3) будем f 1 2              I "р м е л I 1

проводить, пренебрегая членами "О2, где О = max ^—у ) , 1т1г ---^™Lb и УАеР-

,                                                             е-|Е| )

живая члены - (—- )-О (что неявно предполагалось и при выводе (12). Здесь Т -СОТ Э Э 1 характерная длительность импульса: -^ • т^- ~ (^у) • а входящие в О факторы определяют соответствующие масштабы длин: дисперсионного расплывания, затухания и нелинейного самовоздействия.

При таком допущении: 1) вектор А в (3) распадается на нерегулярную и нелинейную части, позволяющие разделить и R = R^^ ♦ R^Hen^; mm   m _

• 2)    необходимое для определения А продольное поле E_z также удается представить в аддитивной квазидинамической форме

  
  
  

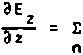
  со .К Э (к е

  У 1   . _____п_

  „ _п К!       -К

  К = О              Эсо

  
  

'экг            _ _

—jT - Е iF-(e -VY) LatK n n n

9Fn at

.. _нел di у Р

е

. .. ЭРнел ё^ div ~^Г

При этом

ления первое

игнорирование в А приближение Е^1* ,

членов "О2 позволяет использовать для его

в котором опущены члены "О. Тогда из (13)

вычис-можно

получить

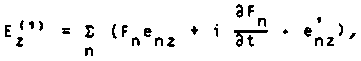
(13.1)

что соответствует квазидинамической структуре поперечного поля (9).

Используя (9) и (13.1)» нетрудно выделить в рамках (3) и (12) влияние нере гулярных (связанных с поглощением) факторов где

г(0) mn

(П - G ) т п

(к +к ) т п

Gn

ы2цеуеп

* V/e^Vy),

(14.1)

Г ’ mn

-

^НН т п

Влияние нелинейной поляризации произвольного вида в рамках (3) описывается (с отбрасыванием членов~0а) выражением:

Анел - п + , ^_ . £).(ша1ГрНел * V djv_P212 >,                       (15)

где по ш дифференцируются (со2ц) и (1/е). При этом, чтобы воспользоваться результатом формул (12), необходимо выделить в рнел медленные амплитуды, положив: —                     — i q z

Рнел = Е Р (t,z,r )ее П .                                                  (16)

П где индекс п соответствует комбинации мод.

•(e.*et)e • exp[(i(k. - k. + k )z]z т.е. q = k. - k. + k . Тогда из (12) и (15)»

1 j m 1       1 j m 1               n i ) m опуская громоздкие преобразования, получим mn где

. (О)  _       1

mn " (km+qn)

_ < 1) _ i mn (k_m+q_n)

П m

co2 -U P

3z

div P

+ Vi(----

e

♦ iq -P„, n nz

.6,.;a^

/3z — )

-n - э ; at :

Е К

пк

amnK

Р ♦ fb „"(div Pn, * ^n^z5 пх 1 I mnK

(17.2)

2       А -I      ° U I

•.„К • 'ir^-’■<“.••<> - 'VT-¹»'⁶».' т n                    т n

ЬщпК

^т'®? e(km*qn>

, 1/Е , k + q т п со

⁶Кт

(17.3)

Полученные общие выражения легко конкретизировать для ряда описываемых ниже

случаев .

Одночастотная ситуация с безынерционной кубической нелинейность». Тогда из [10]

Рнел = а-(Е-Е*)Е ♦ 0(Е-Е)-Е

Одномодовая ситуация

Е = и-е ♦ i|t •

Уравнение эволюции

е*♦ ...) -exp(ikz) .

медленной амплитуды f в рамках указанных допущений примет

вид

|± + k'.                 _ ^ . 3^ = R (у) , „нел                        (20)

dz     die dr о

R^(Y> = ~ Г_о-( * i Г, • |y ,                                                   (20.1)

РНвЛ - ix0 lf|a-f ♦ х^ ~(|f|a«f) + Ax^f- ^- |f|a,                 (20.2)

где

(21 .)

П-U,,

) ,

(21.1)

(при этом a, 3 в дифференцировании no co не участвуют).

Следует отметить, что выражения для U и V в (21) и (21.1) содержат слагав

мые, пропорциональные Vx . Эти слагаемые, как и члены -div^ в операторе попереч* ного усреднения (5) • порядка (|<. г ) от основных. Традиционное пренебрежение ими оправдано лишь в "толстых11 волноводах, либо для простейших ТЕ•поля ризаций.

Влияние дисперсии нелинейности, связанное с коэффициентами х, и Дх, в (20.2) рассматривалось в ряде работ [11*14]. Эти слагаемые становятся существенными для сверхкоротких импульсов (в оптических волноводах * десятки, сотни фемтосе* кунд [ll])- При этом традиционный интерес проявляется, как правило, к симметрич*

ному члену (~х1), а наличие слагаемого ~Дх1 игнорируется [12], что связано с пренебрежением дисперсией модовых векторов е^С^)- Однако даже для простейшей

ЭIn е - , , со _ 3 In к_

ТЕ моды согласно (о) —г---—   —т--- , что обязывает включать в рассмотрение о 1                                    dcodco члены -е* . Тем не менее, как показано ниже, "обнуление" Дх, может быть достиг со нуто для особой нормировки мод, которую каждый раз следует оговаривать. Таким образом, при вычислении х1 и Дх1 возникает необходимость корректного рассмотрения вопроса о нормировке модовых векторов е, например, выбор const в (6). Действительно, нормировочный множитель (обозначим его ц ) является функцией частоты со, т.е. участвует в дифференцировании Зе/Эсо. Детальный анализ показывает: при замене еш(г±) на е = — инвариантность формы (9) для поля Е требует введе-- со          । 3f n" 3af ния вместо f функции f = n^-f * in ' gT--2 ‘ TF= " -'- При этом УРавнение эволюции (20) D-f = R переходит в D-f = R = rj-R ♦ in'" ^ , что Фактически сводится к замене коэффициентов в (20.1 и 20.2):

В частности, как отмечалось выше, надлежащим

(20.2) устраняется слагаемое Дх

т . к .

выбором нормировки моды пш из согласно (20) имеем Дх = 0

при

• •     И    Дх.

п   = т ' —1•

'со      4х

(21 и 21.1) для случая нор

В данной работе конкретизируются коэффициенты мированной ТЕ01 моды осесимметричного волновода (8). Тогда с учетом (?) получим .

= (а+Р) -coV у =     + — • х , Дх = — • х .(23)

ко        8nk '        ко 4V ко'        у ко-

1/4

При этом равенство Аи1 = 0 достигается, если и = V • т.е.

~ у 3/4 ехр(-у Ra/2).

В случае слабонаправляющего волновода, полагая для простоты у_щ = ц_щ = Д_у = Эу =         , имеем:

ГО = 2“ ^^тах' Г1 = -(5 + 2Г1 ‘ ГО'

Х_ф , (а+р)а)Уа/^ , ^ _{= с}^_ _ _L)._Ko, _Дк, = (1 ♦ ^)х_о.

Двухмодовая одночастотная ситуация с безанерционной кубической нелинейностью. 8 этом случае члены, характеризующие дисперсию нерегулярности и нелинейности рассматривать не будем. Тогда при вычислении р^нел (18) можно положить ? = f_i-е,•exp(ik₁-z) * f_а■е₂•exp(iк₃z) . Ограничиваясь требованием фазового синхронизма, из (10), (14), (17) можно получить эволюционную систему:

где

Г m

• 2

СО ЦСУ

amn = а-(е -е*)е  * 0(? -е )е* + m n n         m n п

♦ (1 - 6  )• а-(е -?*)е  * 0-(? -е )?*] .

mn [ n n m          m n nJ

(24.1 )

(24.2)

(24.3)

Структура системы (24) обобщает целый класс задач нелинейной оптики (в част ности, процессы нестационарного ВКР) , описывая ряд практически важных эффектов [15,16]. В простейшем случае осесимметричных TEqi , ТЕ мод, подставляя (8) с учетом (?), получим о = r = М) *<£1£2 R = -L . R , R = I . R .(25)

Rn R1 а 8цк1 z ai k3 n' 338 ai

Для слабонаправляющего волновода при Зу/Эф = 0 имеем                  (25.1)

Г = со Уц- Е.

m2 max

Двухчастотная ситуация с безынерционной кубической нелинейностью. Пусть

-ico -t _                   —ICO t

Е '= Е (t,r)-e m , Рнел = Рнел • е m , (т = 1,2). штт

Тогда с учетом самовоздействия из [10] имеем

Рнел - а •(Е -Е*)Е   + 0 •(Е -Е )-Е* +

1       \ \ 1 1

+ £,.(£,•£*)•£, ♦ n^d.-E*)^ X, (Е,-Е_а)-Е*

и симметричное по индексам 1 и 2 выражение для "РаеЛ. Опуская дисперсию нелиней ности, для медленных амплитуд f (Е = f -е (г, ,со )-exp(ik -z)) с учетом фазовой mm m m х mm синхронизации получим снова систему (24). При этом коэффициенты Г и R опре-m mn деляются выражениями (24.1) и (24.2) с заменой со на со , а для "а теперь имеем mmn а11 = а • (е -е*)е   ♦ р (е -е )e*z а22 = а • (-е -е*)е  + Р (е -е )e*z

1   111 М1 1  1  1'          2   2  2  2    2  2  22'

' а 2 = Еп-(еа-е*)е1 ♦ y^-e^eg ♦ Х^ • (е 1 • е,) е*, а21 = У d/e*)^ + na‘(e*.ea)el ♦ Хд • (е , • еа) е* .

В частности, если обе моды "ет(гл, сот) соответствуют осесимметричной ТЕ01, то из (8) с учетом (?) получим

(а +0 )-to2«и • v

R = ---1---1 —!---1---1 R

11            8п к             * а

_R = (Егпг^-^-и^-у:

12        п-к1•(V1+va)3

(а +0 )'ш²"и • у а а а :

8н к2

п«ка-(v^Vg)3

При этом с заменой со на <от выполняется (25.1).

В заключение авторы выражают признательность И.Н. Сисакяну и А.Ю. Шерману за полезные обсуждения.