Квазидинамическое моделирование старения емкости Li-ion накопителей

На протяжении последних десятилетий наблюдается все возрастающий интерес к экологическим проблемам, в связи с чем вопросы производства так называемой «зеленой» энергии выходят на лидирующие позиции в обсуждениях энергетики будущего. Активная интеграция солнечной, ветровой и других типов возобновляемой генерации везде, где это возможно и экономически целесообразно, приводит к внедрению и развитию технологий промышленного накопления электроэнергии, которые на сегодняшний день представлены не только привычными гидроаккумулирующими станциями (ГАЭС), но также полноценными линейками средств, аккумулирующих электрическую энергию, основываясь на различных физических принципах [1]. К таким технологиям сегодня относятся маховики, накопители энергии на основе сверхпроводимости, Li-Ion накопители электроэнергии, суперконденсаторы, Redox-накопители и другие [2, 3].

Особое внимание при этом следует уделить именно Li-Ion накопителям, которые обладают по сравнению с другими конкурирующими технологиями рядом преимуществ [4], а именно: высоким КПД, оптимальным временем разряда (от минут до нескольких часов) и быстрым временем заряда, сравнительно малыми габаритами, большим количеством циклов разряда до списания, мобильностью и простотой эксплуатации. Кроме того, в ряду развивающихся технологий накопления электроэнергии именно указанный подход на сегодняшний день более прочих приблизился к полноценному промышленному внедрению. Обозначенные особенности очерчивают область применения

Li-Ion накопителей, и эта область оказывается достаточно обширной, включая в себя применение в электротранспорте [1, 5], обеспечение бесперебойного электроснабжения [6], снижение потерь мощности в сетях [7] и выравнивание графиков нагрузки, что может осуществляться как с целью снижения финансовых затрат на покупку электроэнергии, так и для поддержания параметров электрического режима удаленных и изолированных сетей в области допустимых значений [3, 8, 9].

Внедрение систем накопления электроэнергии (СНЭЭ) в целом и Li-Ion накопителей в частности ставит новые задачи перед инженерами энергосистем, одной из наиболее комплексных среди которых оказывается выбор оптимальной емкости и мощности СНЭЭ [10]. Решение данной задачи, а также задачи моделирования работы накопителя на длительных интервалах времени с помощью квазидинамического моделирования широко применяется при оценке экономической и технической целесообразности внедрения СНЭЭ. В такой постановке задачи, как будет более подробно показано ниже, особенности работы накопителя учитываются в виде ограничений, описывающих те или иные характерные особенности: скорость заряда, скорость разряда, КПД, саморазряд и другие.

Тем не менее Li-Ion накопители обладают таким недостатком, как деградация емкости, которая для данных установок может достигать 20 % за 5 лет хранения и использования [1, 3] и в значительной степени зависит от глубины разряда (DoD) и уровня заряда (SoC) аккумуляторной системы при их эксплуатации, что представляет собой дополнительную трудность при моделировании. Так, существующие подходы к учету старения накопителей в процессе эксплуатации при квази-динамическом моделировании работы систем на продолжительных интервалах времени (месяцы – годы) обладают рядом недостатков:

• 1)    метод основывается на физическом, химическом и техническом состоянии системы в каждый из моментов времени, что крайне затруднительно реализовать и моделировать на этапе предварительной оценки эффективности и экономичности предлагаемого решения [11–13];

• 2)    метод рассматривает усредненные глубину разряда и уровень заряда для СНЭЭ на протяжении всего жизненного цикла и не позволяет оценить реальный уровень старения систем в динамике, работа которых по своей сути неравномерна и непостоянна [14–16].

Здесь же следует отметить, что, к сожалению, зачастую деградация емкости СНЭЭ не учитывается в расчетах и анализе, это приводит к чрезмерно оптимистичным оценкам проектов по внедрению Li-Ion накопителей для решения экономических и сетевых задач в энергосистемах: деградация накопителя на 20 % за 5 лет с последующим повышением темпов старения может оказаться серьезным препятствием окупаемости проектов и привести к невыполнению технических требований к вводимым системам.

В данной статье излагается методика учета старения СНЭЭ, которая позволяет на основании паспортных параметров Li-Ion накопителя смоделировать с помощью эмпирической модели его старение при неравномерном графике циклов заряда-разряда без использования сложного математического аппарата. Представленный подход к моделированию процесса старения накопителей разработан на основе эмпирической модели, описанной в статье [14].

Далее в разделах последовательно рассматриваются следующие вопросы: метод, лежащий в основе предлагаемой методики, развитие методики оценки уровня старения Li-Ion накопителей, пример применения методики, выводы.

Методика моделирования старения СНЭЭ

Как отмечалось выше, базой для построения новой модели расчета уровня старения Li-Ion накопителя служит эмпирическая модель, предложенная авторами в статье [14] для моделирования LiFePO4/C СНЭЭ, что хотелось бы подчеркнуть особо. В этой работе авторы предлагают моделировать деградацию двух ключевых параметров СНЭЭ, ограничивающих по мере эксплуатации эффективность данной системы, а именно – емкости и мощности. При этом среди всех влияющих на скорость старения факторов, которые будут перечислены ниже при математической постановке задачи, авторы не рассматривали изменение температуры, т. е. приняли ее постоянной, что допустимо в случае установки систем накопления внутри помещений. В данном исследовании также не рассматривается снижение максимальной мощ- ности накопителя со временем, поскольку, согласно результатам экспериментов [14], за 20 лет моделируемой работы СНЭЭ ее мощность снизилась только на 5 % от номинального уровня, что представляется несущественным на стадии предварительной оценки окупаемости и эффективности внедрения объекта.

В базисном исследовании результирующая деградация Li-Ion накопителя является суперпозицией двух факторов – естественного старения и наработанного износа.

Уровень естественного старения Cсa^ не зависит от числа циклов работы накопителя и посте- пенно возрастает во времени по мере эксплуатации СНЭЭ в зависимости от среднего уровня заряда накопителя SOCa. Данная величина определяет- ся по следующему выражению

/ t X 0,8

CCa, = 0,1723 • е0,74^0С= • (^) ,          (1)

где SOC_a - средний уровень заряда СНЭЭ на цикле, определяемый по выражению

SOCa

^н+^к

2' ^ном

где И⁷ - энергия накопителя в конце цикла, кВт^ч; W_н - энергия накопителя в начале цикла, кВт^ч; К н _ом - номинальная емкость накопителя, кВт^ч.

Наработанный износ C_сус определяется числом циклов п_сус и глубиной разряда на цикле DoD. Данная величина определяется по следующему выражению

Cсус = 0,021 • е"1,95^0^ х х (100 • DoD)0,717 • псус05, (3) где DoD - глубина разряда на цикле разряда, о.е.; определяемая на основании выражения

DoD = 1 - SOCa; (4)

п_сус - число циклов от начала эксплуатации с заданными параметрами заряда (SOC_a,DoD).

Таким образом, уровень деградации для момента t можно определить, суммируя величины, вычисленные по выражениям (1) и (3), по формуле

^Degt = ^Cсус _t ^{+ C}сalt .                      ⁽⁵⁾

При этом рабочую емкость СНЭЭ можно рассчитать для момента t следующим образом:

C t = C н _OM - Deg t .                          (6)

Описанная методика, предложенная в [14], обладает уже указанным ранее недостатком – позволяет производить расчет уровня деградации только для усредненных значений уровня заряда и глубины разряда для всего периода работы. В тех же случаях, когда график зарядов и разрядов накопителей оказывается непостоянным, например, при решении задачи ограничения перетоков мощности по питающим ЛЭП, такой подход может оказаться неприемлемым – необходимо учитывать инерционность процессов деградации во времени.

Электроэнергетика

В данном исследовании представлено развитие описанной выше методологии, которое позволяет перейти в рамках той же эмпирической модели от усредненного прогноза на некоторый период к оценкам уровня старения для каждого интересующего момента времени.

Развитие методики оценки уровня старения СНЭЭ

Задача . Требуется для некоторого момента времени t , оценить деградацию емкости Li-Ion накопителя с учетом неравномерности предшествующего графика циклов заряда-разряда.

Математический метод. В данной работе предлагается использовать метод квазидинамического моделирования, который заключается в последовательном расчете уровня деградации параметров СНЭЭ для каждого момента времени t , на интервале T .

Рекуррентные выражения . Для перехода к квазидинамической модели процесса, предлагается вычислять уровень деградации емкости накопителя от каждой из составляющих для момента времени t , после k пройденных циклов в соответствии с выражением

Ct. = Сном - Deg4k = Сном - (Destl_1.fc_1 + АСса11. + АСсус к),                                      (7)

где C_t . - фактическая величина емкости в момент времени t , после к -1 прошедших циклов, % от С_ном; АС_са11 . - снижение емкости накопителя за At = t , — t , _-1 часов, % от С_ном; АС_{сус к} - снижение емкости накопителя за цикл к , % от С_ном.

Основываясь на формуле (1), можно получить рекуррентное выражение для приращения деградации от естественного старения АС_са11 . для интервала At , :

(          ____________________________ \ 0,8

т^730 •   ^^ •■'    -.М|  —

— 0,1723 • e0,74^0C“i • f— °,8/7ЗО • у 730 \

^De S tj-i,_k-i

0,1723,e °^,74,S0Cai

Л 0,8

)

,

где С0С_а , - средний уровень заряда СНЭЭ на интервале At , , о.е., определяемый по выражению

С0Са.

^_^л

2" ^ном

At = 1 - шаг моделирования, ч.

Аналогичным образом, на базе формулы (3) выводится рекуррентное выражение для приращения деградации от наработанного износа АС_{сус к} для цикла работы к :

АСсус к = 0,021 • e-1,95"50C“k • (100 • DoD^0,717 •

^De S tj-i,_k-i

. 0,021"6 ^1,95,SOCak ,(100,DoD _k ) °,⁷¹⁷

") + А^сус

—

— 0,021 • e ^-1 , ⁹⁵ " ^50C “k • (100 • DoD_k) ⁰ , ⁷¹⁷ •

___________ ^De s ti-i,k-i ___________ 0,021"e ^-1,95,5OCnk "(100"DoD _k ) °,⁷¹⁷ ,

где 50Сак - средний уровень заряда СНЭЭ на цикле к в интервале от t,-1 до t,, о.е., определяемый по вы- ражению

50Са. = nk

^i-A.

² " ^ном

DoD_k - глубина разряда СНЭЭ на цикле к в интервале от t , _-1 до t , , о.е., определяемая по выражению

DoD k = 1—С0С к . (12) Ап_сус = 1 - шаг учета циклов.

Таким образом, используя выражения (7), (8) и (10), можно смоделировать процесс работы СНЭЭ при алгоритме управления системой любой сложности и оценить конечную величину деградации емкости системы.

Алгоритм . На рис. 1 приводится блок-схема моделирования процесса старения Li-Ion накопителя.

В первоначальный момент времени, согласно представленному алгоритму, задаются начальные значения времени t , номера цикла к и уровня деградации Deg_{0 0}. В общем случае в соответствии со схемой эти величины первоначально равны нулю, что соответствует началу работы нового накопителя электроэнергии.

Расчет производится для всех моментов t , в заданном интервале T и прекращается, когда этот интервал исчерпан, что отражается первым условием на диаграмме. Энергия накопителя в начале и в конце интервала определяется в соответствии с электрической моделью накопителя и режимом его работы, в зависимости от мощности заряда/разряда системы на некотором интервале.

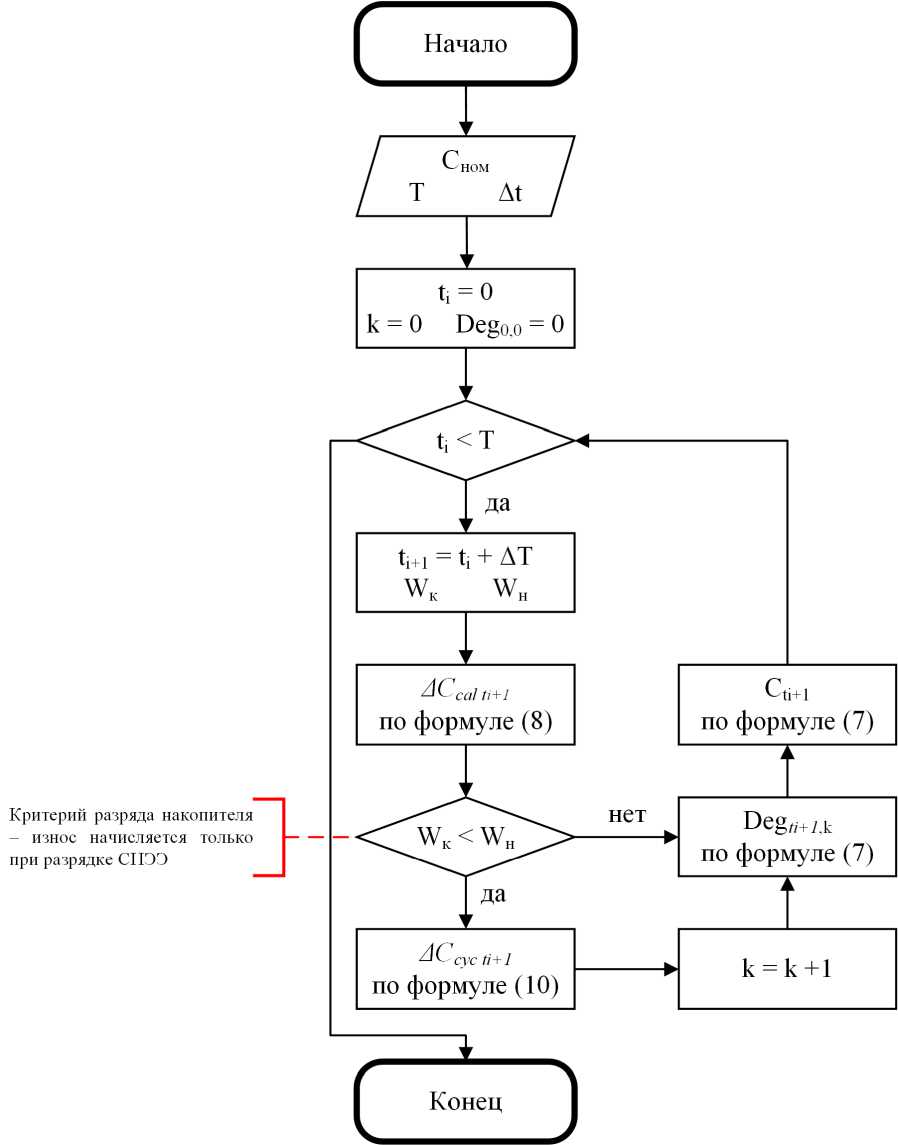
Рис. 1. Блок-схема алгоритма моделирования старения Li-Ion накопителя

Также в данной методике принято, что накопленный износ системы прирастает только в интервалы времени, когда происходит разряд накопителя, что и считается циклом. Данная особенность учитывается вторым условием в блок-схеме, где происходит сравнение энергии в начале и конце интервала. Важно заметить, что условие может быть изменено в зависимости от модели накопителя, поскольку в ряде случаев оно может оказаться некорректным. Например, при простое системы накопления, если учитывается саморазряд системы, происходит постепенная потеря энергии с течением времени, но разрядом СНЭЭ с точки зрения моделирования старения это считать никак нельзя. В таком случае критерий должен быть доработан либо заменен.

Результат моделирования. Результат расчета представлен рядом значений уровня снижения емкости накопителя относительно номинальной величины для всех t , интервала T .

Применение методики моделирования старения СНЭЭ

В качестве примера применения предлагаемой методики рассмотрим результаты моделирования работы СНЭЭ для T = 5 лет, параметры которой приводятся в табл. 1, для двух сценариев.

Электроэнергетика

• 1.    Сценарий A . В те че ние 5 л е т на коп ител ь р а з ряж а е тс я ка ждый день в пе риод с 12: 00 до 13:00 до 20 % св ое й ном и на л ь н ой ем кос т и, пос л е ч е го з а ряж а е тс я в пе риод с 13: 00 до 15: 0 0 на в е л ичину 40 % за час;

• 2.    Сценарий B . В тече ни е 5 ле т н ако п и тел ь:

• а)    в з и мн и й п ери од (с окт яб ря по м а рт) разряжается к а ж д ый д е н ь в п ери о д с 9 :0 0 д о 1 0 :0 0 д о 20 % сво ей н о мин а льн о й ем к о сти , п о с ле ч ег о заряжается в пер и од с 1 0 :0 0 д о 1 2 :0 0 н а ве л и чи ну 4 0 % за час, и в период с 1 4 :0 0 д о 1 5 : 0 0 д о 2 0 % своей н о мин а льн о й емк о с ти , п о сл е ч ег о зар яжае т с я в п ер и о д с 1 5 :0 0 д о 1 7 :0 0 н а ве л ич ину 4 0 % за час;

• б)    в л ет ни й п е р и од (с ап реля п о се нт яб рь ) ра зр я ж ае тс я каж ды й день в пе р иод с 12: 00 д о 1 3:00 до 20 % с в ое й ном и на л ь ной ем кос ти, посл е чего зар я ж ае тс я в пе риод с 13: 00 до 15: 00 на в ел ич ин у 40 % за час.

Ре з у л ьта ты м одел иров ани я пре дс тав л ены графиче с ки на рис . 2, где пока з а ны тра е к тории изменения емкости накопи т ел я в ра с с м а трив а е м ый

период, и в табл. 2, которая предоставляет численные данные о состоянии системы в конце периода для двух сценариев работы.

Расчетные данные демонстрируют, что разработанная методика позволяет учесть неравномерный режим работы накопителей. В частности, для сценария В конечный износ оказывается большим, что продемонстрировано численно и графически.

Необходимо обратить внимание на то, что в неизменном виде предлагаемый алгоритм подходит не всем Li-Ion накопителям, поскольку он не учитывает индивидуальные особенности старения тех или иных видов накопителя, которые, как правило, производитель задает в виде гарантийного числа циклов работы при заданных средних уровнях заряда и разряда. Предложенная модель может быть адаптирована пользователем путем изменения первых множителей уравнений (8) и (10), таким образом, чтобы при регулярном разряде за заданное число циклов накопитель достигал нормированного уровня износа.

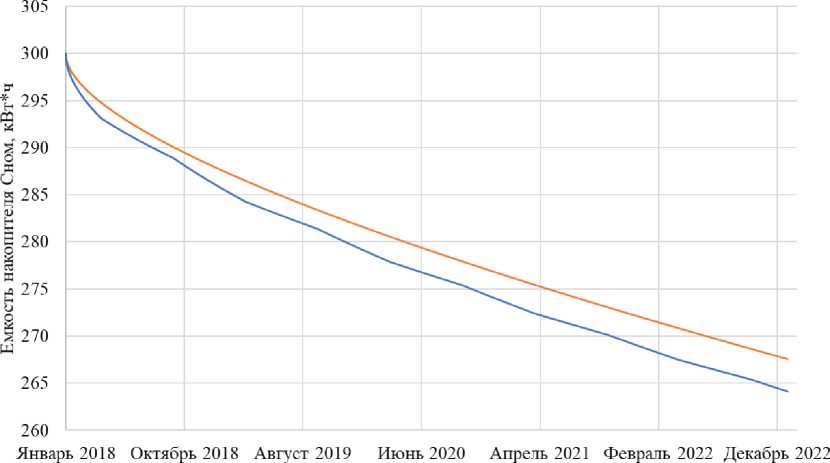
Сценарий А --Сценарий В

Паспортные параметры тестовой СНЭЭ

Таблица 1

Номинальная емкость С ном , кВтч	Г лу б и на раз ряд а D oD , %	КПД, %	Скорость заряда	Скорость разряда
300	20	98	1С	0,5С

Рис. 2. Траектории деградации емкости СНЭЭ в рассматриваемый период для двух сценариев работы

Численные данные о состоянии СНЭЭ в конце периода для двух сценариев работы через 5 лет работы

Таблица 2

Сценарий	Е с те с тв енное с та ре н ие , %	Наработанный износ, %	Уровень деградации емкости, %
А	6,075	4,737	10,812
В	5,754	6,206	11,960

Заключение

Предлагаемая методика, как показал тестовый расчет, может оказаться полезной при моделировании СНЭЭ в оценочных расчетах эффективности проектов по внедрению Li-Ion накопителей, режим работы которых сложно охарактеризовать некоторыми постоянными характеристиками.

В дальнейшем представляется интересным ввести полную модель накопителя с учетом всех существующих технических особенностей и ограничений для корректного моделирования работы таких систем в задаче расчета режимов и квазиди-намическом моделировании энергосистем.