Квазиклеточные сети как обучаемые структуры

В многочисленных работах [1,2,3,4,5 и др.] рассматривается свойство обучаемости дискретных структур. Фактически, обучаемость предполагает некоторую настройку параметров дискретной структуры, влияющую на её функционирование[2,4]. При организации обучения предполагается наличие некоторого набора входных параметров:

X вх =( X 1, X 2,...) ,(1)

в ответ на которые дискретная структура выдаёт на выходе вектор вида:

Yвых =(Y1,Y2,...).(2)

Предполагается подача на вход обучающего множества векторов:

E ={ X вх1 .Xвх2 ,...} ,(3)

при которых формируется строго определённое множество выходных векторов:

O = {Yвых1,Yвых2, ...} .(4)

Предполагается, что производится настройка параметров дискретной структуры,      позволяющая      по      заданному      входному вектору Xвхi∈ E однозначно получить выходной вектор Yвхi∈O . Целью обучения является возможность подачи на вход настроенной дискретной структуры и обработки в ней вектора X ' вх6E [4].

Особое внимание в вопросах обучаемости дискретных структур следует уделить квазиклеточным сетям, дискретным структурам, не имеющим сигнатуры (рис. 1) [6,7]. Основным предназначением указанных дискретных структур является реализация проектирования и моделирования систем, сводящихся к рассмотрению потоков при различных предметных интерпретациях[6,7]. Базовое представление о квазиклеточной сети было дано на основе некоторых преобразований графа, являющегося двусортным множеством[6], т. е. обладающий носителем и сигнатурой. В отличие ряда дискретных структур, в т.ч. нейронных сетей, квазиклеточные сети не обладают сигнатурой, однако предусмотрены методы их синтеза на основе графов [8]. Однако квазиклеточные сети синтезируются и другими методами, основанными на манипуляциях над клеточным автоматом, а также моделированием поведения микрообъекта[8], синтезирующего клетки.

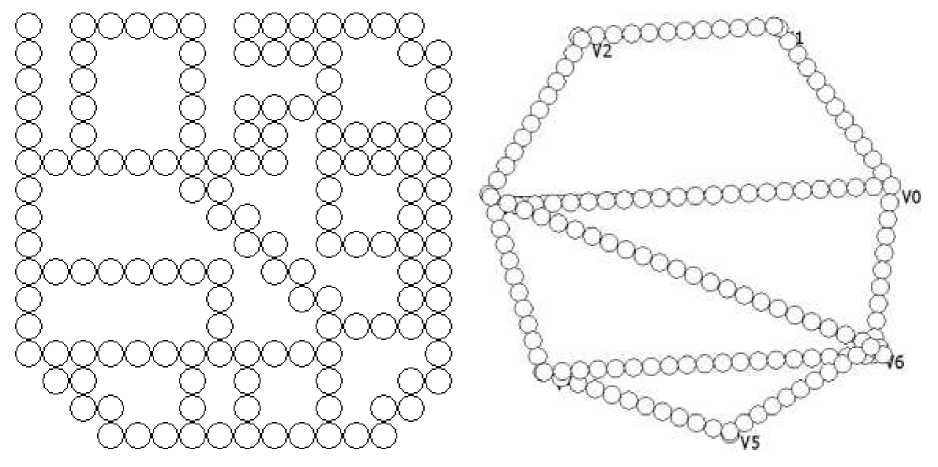
Рис. 1. Квазиклеточные сети.

В условиях квазиклеточных сетей рассмотренные выше аспекты обучения также являются актуальными, что показывает обучаемость квазиклеточных сетей как дискретных структур. Учитывая, что каждая клетка задаётся в виде[7,8]:

Q i =( B_t, C i , S i ) (5)

где ^B i – неизменные (базовые) параметры клетки (от англ. Basic), ^C i – параметры клетки, изменяющиеся при прохождении фишек через клетку (от англ. Changeable), ^S i – параметры фишки как объекта, находящегося в клетке, т. е. переменные состояния (фазовые переменные) клетки (от англ. State); становится очевидно, что в качестве параметров, настраиваемых в процессе обучения, выступают величины из группы ^C i . В процессе циркуляции по определению указанные величины изменяются.

В качестве входных векторов при обучении квазиклеточной сети следует рассматривать состояния генератора ^S g ⁽ t' ) , в каждый момент времени (динамической характеристики квазиклеточной сети), т. е.:

X вх = ( S g ( t' 0 ) , S g ( t' o + 0 ) , S g ( t' o + 2 0 ) , S g ( t' o + 3 0 ) , ... ) . (6)

Соответственно в качестве выходного вектора следует рассматривать состояние стока S o ⁽ t' ) [7]:

Y вх = ( S o ( t' 0 ) , S o ( t' o + 0 ) ,S_o ( t' o + 2 0 ) ,S_o ( t' o + 3 0 ) , ... ) . (7)

Следует отметить, что (6) и (7) представляют собой наборы входных и выходных данных, распределённые во времени (или в зависимости от динамической характеристики квазиклеточной сети). В такой ситуации за некоторое время моделирования обрабатывается только один набор данных. Ещё один способ представления входных и выходных векторов предполагает, что каждый генератор и сток позволяют каждый момент времени получить соответственно одну компоненту входного или выходного вектора:

X вх ( t' )=( S gi ( t' ) ,S g2 ( t ') ,S g3 ( t' 0 ) , ... ) ,                            (8)

Yвы,(t')=(So,(t'),So2(t'),So3(f0),...) .                          (9)

Таким образом, в каждый момент модельного времени (каждый такт изменения динамической характеристики квазиклеточной сети) ^{t '} квазиклеточная сеть формирует пару векторов ⁽ X в, ⁽ t' ) , Y вых ⁽ t' )) .

Таким образом, оценена обучаемость квазиклеточной сети, сравнимая с обучением ещё ряда дискретных структур. В данном случае обучение базируется на обработке векторов входных и выходных данных и настройку изменяемых параметров элементов квазиклеточной сети.

Следует также отметить, что учитывая возможности измерений параметров квазиклеточных сетей, в качестве генератора и стока могут быть рассмотрены практически любые клетки сети, в которых фиксируются состояния.

Рассмотренное выше свойство обучаемости квазиклеточных сетей обладает аналогией с обучением других дискретных структур. Учитывая, что целью любого варианта обучения фактически является получение дискретных структур, функционирование которых отвечает определённым требованиям. Следует отметить, что достижение определённой функциональности в квазиклеточной сети сводится не только к настройке её параметров, но и формированию её структуры. Исходя из этого, особое внимание следует уделить вопросам обучения квазиклеточной сети уже на этапе синтеза её структуры. Фактически, синтез структуры предполагает настройку базовых параметров B i квазиклеточной сети, в отличие от обучения, основанного на изменении ^C i . Для интуитивно понятного представления задачи обучения квазиклеточной сети на этапе синтеза, представим ситуацию, при которой необходимо моделировать поток частиц (объектов), движение которого осуществляется в соответствии с некоторой моделью поведения по определённому множеству траекторий[8].

Фактически клетка в квазиклеточной сети является и единицей потока и единицей пространства. Тогда, согласно методу генерирующей фишки, фактически синтезируется структура сети, а дальнейшее моделирование множества объектов сводится уже к циркуляции в квазиклеточной сети по синтезированным траекториям.

Таким образом, синтез квазиклеточной сети на основе поведения микрообъекта фактически является одним из направлений обучения квазиклеточных сетей, при котором обучение сводится к формированию структуры квазиклеточной сети и переходу от объектно-ориентированного микромоделирования к квазиклеточному моделированию[2,8].

Ещё один аспект, тесно связанный с обучением квазиклеточной сети, связан со снижением вычислительных затрат на её реализацию её функционирования. Фактически, моделирование функционирования квазиклеточной сети предполагает, что каждый такт времени (динамической характеристики) θ рассматривается изменение состояния на всём множестве:

Г Q = { Q 1, Q 2, ... } { 0 , = ( В„С i- S i ) ’

в котором проверяются возможности осуществления переходов ^Qi ^{→ Q}j , образующих циркуляцию. В случае, когда в процессе циркуляции рассмотрение каждой клетки нецелесообразно, фрагмент квазиклеточной сети следует рассматривать в виде чёрного ящика[]. На таком участке предполагается        наличие        клеток         ^Qвx ⁼⁽ B ex -C вх ,S вх ) и

Qвых ( B вых , Cвых, S вых) . Указанное справедливо для участка квазиклеточной сети:

* = { Q' i, Q* 2, ... } Q' ⊂ Q Q вх ∈ Q' ^Qвых ^{∈ Q'}

,

при этом не существует последовательности переходов состояния, при которой осуществляется переход из ⁰ вых в ^Q вx , т. е. ^Qвых - Q . , Q . - Q . + 1 , ^Qi + 1 ^Qi + 2 , . . , ^Qi + n ^{> 0}вх для которых

V i : Q,^Q* . (12)

В такой ситуации участок квазиклеточной сети соответствует определению чёрного ящика, для которого определены клетки, являющиеся входами и выходами, соответственно ^Q вх и ^Q вых . Очевидно, что входы и выходы чёрного ящика наиболее интуитивно понятно представлены в квазиклеточных сетях с направленной циркуляцией и микроциркуляцией. Именно для таких классов квазиклеточных сетей характерно строгое ограничение циркуляции, позволяющее строго отличать входные клетки от выходных и организовывать циркуляцию от входа к выходу.

При наличии динамической характеристики t* = 0, ^ - ² B , ³ ^ ,^... на входах и выходах чёрного ящика снимаются величины S вх ⁽ t' ) и S вых ⁽ t* ) . Таким образом, работа рассматриваемого участка квазиклеточной сети ^Q' эквивалентна работе указанного чёрного ящика.

Таким образом, рассмотрены возможности использования квазиклеточных сетей, как обучаемых дискретных структур. Следует отметить, что в данной работе основное внимание уделяется вопросам синтеза и моделирования квазиклеточными сетями. При этом приведены только оценки возможности обучения квазиклеточных сетей и их сходства с другими типами обучаемых дискретных структур. Более детальные особенности обучения зависят от конкретных алгоритмов и предметных задач, реализуемых на квазиклеточных сетях.

Таким образом, рассмотрены особенности, доказывающие обучаемость квазиклеточных сетей по трём аспектам – настройке параметров клеток в зависимости от циркуляции, обучения на этапе синтеза и замены участка квазиклеточной сети на заранее обученный «чёрный ящик».