Квазиодномерный расчет температурного поля твердотельных катодов плазмотронов

В работе рассмотрена обобщенная задача теплофизического состояния составных катодных узлов сильноточных плазменных систем [1]. Она основана на решении нелинейного уравнения нестационарной теплопроводности:

с р ^d^ = div(Xgrad T ) + q_v д t                         "

с учетом основных видов теплообмена электродного узла с внешней средой, где T – температура, c – удельная теплоемкость, р - плотность материала, X - коэффициент теплопроводности, q _V - объемная плотность внутренних источников и стоков, обусловленных различного рода физико-химическими процессами выделения и поглощения энергии.

На рис. 1 показана модель типичного катодного узла плазменных устройств. Для плазмотронов наиболее работоспособными являются конструкции, состоящие из центрального стержневого электрода – вставки I из тугоплавкого металла (например, чистый или активированный вольфрам), запрессованного в медный цилиндрический корпус катодного узла – обойму II.

Длина вылета катода варьируется от L c = 0 (заделка заподлицо) до L c / d 1 >> 1 (длинный катод).

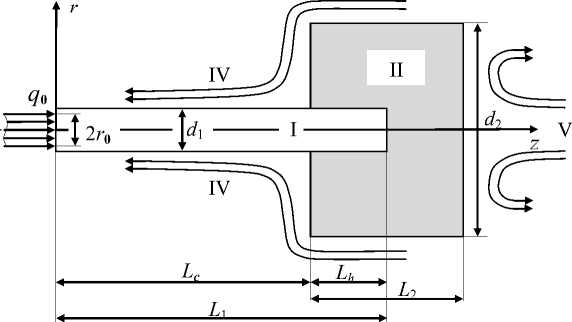
Рис. 1. Схема составного катодного узла плазменных устройств.

I – катод (вставка), II – корпус узла (обойма), III – плазма разряда, IV – плазмообразующий газ, V – теплоотвод (жидкость)

В квазиодномерном методе влияние массивной охлаждаемой обоймы на температурное поле вставки в постановке задачи заменяется граничным условием I рода, а сложный теплообмен через боковые поверхности электрода учитывается введением в одномерное уравнение теплопроводности так называемых эффективных объемных источников и стоков энергии. Это приближение подходит для расчета температуры длинных катодов с диффузной привязкой разрядов при достаточно большой токовой нагрузке, когда площадь контакта разряда близка к поперечному сечению электрода ( r 0 ® R 1 ) и изменением температуры по радиусу можно пренебречь.

В данном случае уравнение теплопроводности (1) записывается только для вставки I (рис. 1) в виде:

c i p m д Т = ^гГм т ) d T 1- 2^{а т )}( т - T g ) - ^{2s( Tю}B (т ⁴ - T m ⁴) + j^ ^( t )   ⁽²⁾

8 t   8z L      8z J    r                r где a(T) - коэффициент конвективной теплоотдачи, e(T) - интегральная излучательная способность, оB - постоянная Стефана-Больцмана Tg и Tm - температуры плазмообразующего газа и окружающей среды.

Для установившихся тепловых режимов численно решается стационарное уравнение теплопроводности стандартным итерационным методом Рунге-Кутта с учетом известного из эксперимента удельного теплового потока из плазмы q 0 :

q о = -Х ( T) 8 T(0)/ 8 z

Второе граничное условие задается на холодном торце катода:

T ( L 1 ) = 300 K

Квазиодномерный метод позволяет оптимизировать температурный режим и выявить вклад каждого из составляющих уравнения (2) в энергобаланс катода.

Рассмотрим термоэмиссионные катоды плазмотронов с обжатой дугой, широко используемых для сварки и резки не только тонких (0,15 – 0,5 мм), но и толстых листов металлов [2]. Они особенно эффективны в автоматизированных процессах, где их ресурс непрерывной работы становится наиболее важным элементом технического цикла. На рис. 2а показаны полученные в расчетах осевые распределения температур в цилиндрическом W – катоде фиксированной длины L_c = 20 мм с диаметром 5 мм при различных значениях тока дуги. Экспериментальное оптимальное распределение температуры соответствует току 350 А (пунктир), что подтверждается графиками 4 и 5.

а)

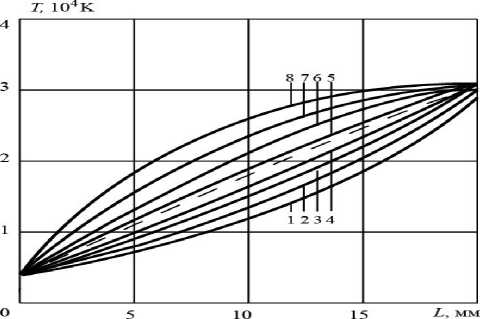
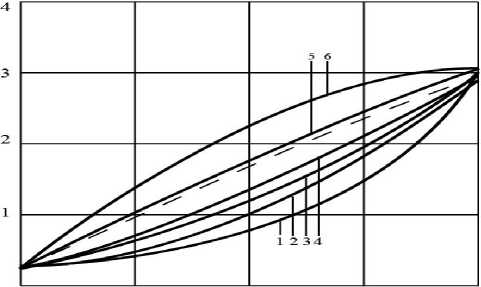
Рис. 2. Осевые распределения температур катода. а) d ₁ = 5 мм, 1 – 8 ток соответственно 50, 100, 200, 300, 400, 500, 600, 700 А. б) d ₁ = 3.5 мм, 1 – 6 ток соответственно 50, 75, 100, 125, 150, 200 А

б)

Т, 1О4К

°          5          Ю         15     L, мм

На рис. 2б представлено распределение температуры для электрода с диаметром 3,5 мм. Видно, что к экспериментально найденному распределению (пунктир) наиболее близка расчетная кривая, соответствующая току 150 А. При реализации данного токового режима ( I = 125–150 А) электрод функционирует с наибольшим ресурсом [2]. Таким образом, графики показывают, что квазиодномер-ный метод расчета применим для оптимизации температурного режима стержневого тугоплавкого катода, так как дает результаты, практически совпадающие с данными эксперимента и обобщенной задачи [1].

Б.Д. Цыдыпов. Нестационарная физико-математическая модель процессов в сильноточных плазменных системах

Из расчетов следует, что наиболее сильное влияние на термический режим катодов оказывает их диаметр d 1 .