Квазиоптимальный алгоритм фильтрации цифровых полутоновых изображений марковского типа

Проблема восстановления цифровых полутоновых изображений (ЦПИ), искаженных шумами, несмотря на огромное число работ, посвященных ей, остается не менее актуальной. Наибольший интерес для практики представляет фильтрация динамических ЦПИ (видеопоследовательностей).

Для фильтрации видеопоследовательностей ЦПИ в реальном масштабе времени необходимы «быстрые» алгоритмы фильтрации. Среди известных алгоритмов обработки ЦПИ наиболее быстрыми и эффективными являются нелинейные алгоритмы.

Предложенный в [1-2]метод нелинейной фильтрации ЦПИ марковского типа с дискретными аргументами отличается от других известных методов фильтрации тем,что ЦПИ,представленные g-разрядными двоичными числами,разделены на g разрядных двоичных изображений (РДИ), которые являются двумерными цепями Маркова с двумя равновероятными значениями.Такой подход к решению задачи фильтрации ЦПИ существенно упрощает реализацию алгоритма нелинейной фильтрации ЦПИ.

Основныевычислительныезатратыприреали-зации алгоритмов нелинейной фильтрации ЦПИ, синтезированных в [1-2], связаны с необходимостью вычисления нелинейных функций. Аппроксимация нелинейных функций, предложенная в [2], существенно уменьшает объем вычислений, но справедлива только при отношении сигнал-шум на входе приемного устройства больше 0 дБ. В данной работе предлагается аппроксимация нелинейных функций с менее жесткими, чем в [2], условиями применения, которая позволяет значительно сократить количество вычислительных операций и расширить диапазон допустимых отношений сигнал-шум на входе приемного устройства в сторону малых значений.

Уравнения нелинейной фильтрации элементов ЦПИ

Будем считать, что осуществляется классическая построчная развертка ЦПИ. Разработка и исследование алгоритмов обработки ЦПИ базируется на математических моделях (ММ), адекватных реальным изображениям. Возьмем в качестве ММ одностороннее марковское случайное поле (ОМСП) на несимметричной полуплоскости (НСПП) (двумерную дискретнозначную цепь Маркова ^{2 g} дискретными значениями). Представим ЦПИ набором из g РДИ, что позволяет свести построение ММ ЦПИ к построению ММ РДИ [3].

Зададим в l-м РДИ (рис. 1) для элемента p ( lj окрестность Л ⁽ 4j. в виде [4]:

л5 = {Н?j-1, ^-v, ^-’и-1},1 = 1 g, i = 2, m, j = 2, n, и будем считать, что РДИ представляет собой стационарное поле марковского типа с автокорреляционной функцией вида [4]:

_r(l )                ( l ) ..( l )                    ( l ) ²                    ( l )               ( l )

rq,s =ELHi, j 'Ц +q, j+s J = °H eXp{—ai |q| -a2 |s|} , где E [•] - имеет смысл математического ожи-(l )2

дания; σ _μ – дисперсия сигнала изображения;

( l )       ( l )

α ₁ , α ₂ – множители, зависящие от ширины спектральной плотности мощности случайных процессов по горизонтали и вертикали.

На рис. 1 представлена ММ двумерного l -го РДИ (а), с окрестностью Л^ j. элемента v ⁽ ₄ l ) (б), где приняты обозначения:

v ( l >  = p i | ^v? ^ ;v 3l >  = Д_/Ч^ ) = , ( | ) .

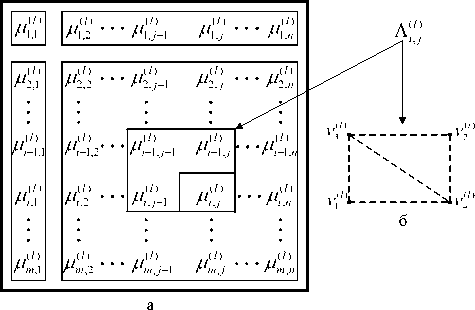
Риc. 1. ММ l-го разряда ЦПИ. а – ОМСП на

НСПП; б - окрестность Л ^{( 1} j элемента v 4l )

Пунктирные линии на рис. 1(б) указывают на наличие статистических связей между элементами окрестности Л(1) = {v(l) V2) v3l)} и элементом V(l)                      j v 4 .

В качестве ММ марковского РДИ примем двумерную цепь Маркова на НСПП с двумя равновероятными состояниями M 1 , M 2 ( Р 1 ( vrl ) ) = Р 2 ( у Г ¹ ) ) , l = 1, g , r = 1,4 ) и матрицами вероятностей перехода (МВП) и з с остояния M _α в соседнее состояние M в ( а,в = 1,2 ) по горизонтали и вертикали изображения, соответственно:

n( l ) =	Г i Ji) ⎡π 11	1 Ji)! π 12 ⎤	, 2 n( l ) = ⎥	‘2 n ( 1	2 Jl)! π 12 ⎤ ⎥
	1 Ji) ⎣π 21	1 Ji ) π 22 ⎦		.2 nf*	2 K(l * π 22 ⎦

На основе такой ММ в работе [1] был синтезирован алгоритм нелинейной фильтрации ЦПИ. Уравнение нелинейной цифровой фильтрации l -го РДИ, являющегося составной частью ЦПИ, имеет вид [1]:

u (^)) = f (Mi (v4)))—f (M2 (v4)))

+u ( v ^{( l} ) ) + z ^ u ( v ( l ) ) , ¹ П ^{( 1} ) ^j + +u ( v2 ) ) + z [ u ( v2 ) ) , ² n ^{( l} ) ]-

+

¹ )                          ( l ) ³ ( l ) ""I

• U V3  — zu V3 , П , где

u

(vrl))=ln (Pi (vrl) у P2 (v(rl)))

-

логарифм

отношения апостериорных вероятностей дис- кретного параметра двоичных импульсных сигналов, однозначно связанного со значением элемента vrl), l = 1,g - номер РДИ, r = 1,4;

f (Ml (v4l))) - f (M2 (v4l)))

– разность логариф-

мов функций правдоподобия дискретного пара- метра двоичных сигналов, которыми передаются элементы l-го РДИ.

Вся априорная информация о статистической зависимости элементов l -го РДИ сосредоточена в слагаемых вида:

dzu            dzu k „ = lim —= -1, k+„ = lim —=

-∞                        +∞ u→-∞ du              u→+∞ du

^b -∞

= lim ( z ( u ) - k_ _m u ) = In —— , u→-∞

π _αα

-1,

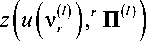
(l)             (l)(

л:/ + п2/ exp {- u ( v r ) )}

11      21             r r (l) , r (l)

П 22 ) + n ( 2 exp { u ( v r ) )}

^b +∞

= lim ( z ( u ) - k _+m u ) = 1п^{П аа} . u→+∞ π αβ

При больших значениях

r = 1,3 , l = i,g , r n O l e — элементы соответствующих М ВП от значения M _α к значению M_β ( а,в = 1,2 ) : по горизонтали 1 ^п () , вертикали ² П ^{( 1} ) и диагонали ³ П ^{( 1} ) = ¹ П ^{( 1} ) • ² П ^{( 1} ) .

для z ( u ( v rl ) ) , ^r n^{( l} ) )

|u ( v⁽‘ ) )| выражение

упростится и примет вид:

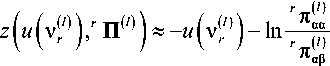
u ( v ⁽ rl ) ) <<  0 ;

В качестве критерия различения значений элементов l -го РДИ используется критерий идеального наблюдателя [5], в соответствии с которым решение о значении параметра в принятой реали-

зации сигнала производится на основе сравнения логарифма отношенияапостериорных вероятностей фильтруемого элемента u ( v ⁽ ₄ l ) ) с некоторым порогом Н, выбранным таким образом, чтобы минимизировалась средняя вероятность ошибки.

В симметричной системе порог H = 0 .

r „r(l)

z ( u ( v rl ) ) , r n ( l ) ) ~-u ( v ⁽ _rl ) ) + in— aa , r ⁿ ae

u ( v ^l ) ) >>  0 •

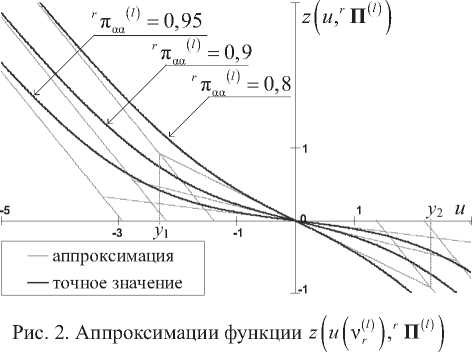
На рис. 2 представлены фрагмент графика функции z ( u ( v rl ) ) , ^r n^{( l} ) ) и касательные линии, которыми эта функция аппроксимируется.

Аппроксимации нелинейной функции

При реализации уравнения (1) большая часть вычислительных ресурсов расходуется на вычисления имеющихся в алгоритме нелинейных функций (2). Упростим вычисление нелинейных функций (2) в уравнении (1). Для удобства вычислений будем считать, что r п ⁽ 1 ) = r п 22 = r п аа , r n ^{( l} ₂ ) = r п 27 = r п ⁽ _ар ( ^а,в = 1,2 , а ^ в ). Тогда функция (3) запишется в виде:

r (l) r (l)                     (l )\j z (u (vrl)) , n(l))

^п аа +       exp , u ( ^v r ) )}

. (3)

r (l ) I r (l ) C / ( l ) \) ^п аа + <■ exp ( u ( ^v r ) )}

Разложивэкспоненциальныефункцииилогарифм в степенной ряд Тейлора вблизи точки u (vrl)) = 0,

Г ( l )      1

при п аа ^ 1 , и ограничившись первыми членами разложений, (3) можно упростить:

z (u (vrl)); n(l)) «-2 (r n2J • u (vr))).

Анализ графиков, представленных на рис. 2, позволяет заметить, что принятые аппроксимации достаточно близки к точному значению исходного выражения (3).

Координаты точек пересечения касательных r ( l )          r ( l )

y 1 и y2 (рис. 2) выражаются из равенства аппроксимаций функции:

Проведем z ( u ( v rl ) ) , r n^{( l} ) )

касательные к функции в точках u = ±w (рис. 2):

z (u) ~ k u + b , z . (u) ~ k^ u + b , u →-∞ -∞ -∞ u→+∞ +∞ +∞ где k - угловые коэффициенты, b - свободные члены уравнений касательных, соответственно равные:

r тт(‘ )

- r y (l₂ ¹ m in— ^{aa y} 1,2           r ⁽l)

π αβ

^r ji l '=

- In

r „r(l) παα r JZ) παβ

r

= -2f^r Л⁽¹ )

( ^П «в

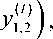
r л⁽¹ ) π αα

^1П r „V ) ' (l) ^П ав y 2 =.

При r п ав = 0,5 координаты r У\ ) = r У 2 ) = 0 ■

С учетом приведенных аппроксимаций уравнение (1) упростится следующим образом:

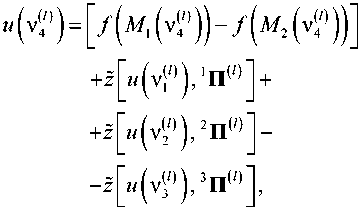
где

Z ( u ( v . ¹ ) ) , ^r П ^{( 1 )} ) =

C.1) • sign(u (V/))); |u (v*.1) )| > ry2),(5)

B.) • u (v(1)); |u (v.1) )| < ry2), r J')

C ^{( 1})=1_n—aa_ ^(l)=1- 2-(^rH^(l )    ^rv⁽¹ ) = ^r

Cr     ln r „(1) ’ Br     1 2 ( Пав ) ’  y2     R)l)

παβ                               Br r = 1,3 , l = l,g ■

Таким образом, нелинейные функции (3) мо- гут быть замещены постоянной добавкой при больших значениях |u (v(rl) )|

, или линейным вы-

ражением при малых значениях

| u ( v rl ) ) ,

что

многократно сократит вычислительные затраты.

Уравнения нелинейной фильтрации элементов последовательности ЦПИ

Будем считать, что последовательность РДИ представляет собой трехмерный дискретнозначный марковский процесс с двумя пространственными координатами i , j и третьей k – временной [3].

Зададим в l -м РДИ (см. рис. 3) для элемента ^ ( l \k окрестность Л\_к в виде [3]:

Л(l) = Ul).v(l).v(lL^lL^lL^l) V(l)i l = yy i, j,k     {V1 ; v 2  ; v3  ; V1   ; v 2   ; v3   , v4   } , 1      ,g ,

¹ П ^{( 1} ) =

Г i Ji)

⎡π

i Ji) ^π 21

i Ji)! π12⎤ i Ji) π22 ⎥⎦

⁴ П ^{( 1} ) =

, ² n ^{( l} ) =

Г 4 Ji) ⎡π ₁₁

4 Ji)

⎢⎣ ^π 21

Г 2 Ji )

⎡π

2 тт(1 ) ^π 21

4 Ji ) "

^π 12 ^⎤

4 Ji) ^π 22 ⎥⎦

■

2 Ji JI π 12 ^⎤

2 Ji) ^π 22 ⎥⎦

,

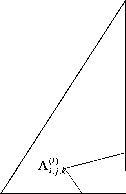
На основе такой ММ в [2] был синтезирован алгоритм нелинейной фильтрации последовательности ЦПИ. Применив аппроксимации (5) к уравнению нелинейной фильтрации последовательности ЦПИ [2], получим уравнение квазиоптимальной фильтрации последовательности ЦПИ, которое для l -го РДИ запишется в виде:

• ( l )          ( l )                    ( l )          ( l )                    ( l )           ( l )

где    v() -u'J-^, v2) = ^J,J,k, v) = ^4,-^, v (l) = J1)         v(l) = J1)             v(l) = J1)

• ^v 4 H, j , k ,          ^V 1 H, j - 1,k - 1 ,          ^v 2 H / - 1, j , k - 1 ,

,( l) _ ( l )                 J ) _ ( l )

• ^v 3 = ^ i - 1, j - i, k - i , ^v 4 = ^ i , j,k - i , и будем считать, что последовательность РДИ представляет собой стационарное поле марковского типа с автокорреляционной функцией вида [3]:

⁽ l )           ⁽ l ) 2                    ⁽ l )               ⁽ l )              ⁽ l )

r q,s,t = ^СТц exp{-^a i |^q| ”^a2 |^s| ”^a 3 |t|} ■

u ( V4l) ) = f ( Ml ( V(4 ) )) - f ( M2 ( V4l)))

+

+ z %	⎡ u	l IV1 )	, 1 n ( l ) J	+ z % ⎡	u (	l v 2 ) ,	2 n ( l ' J-
- z %	⎡ u	%(l )1 V 3 )	, 3 n ( l ) J	- z % ⎡	u (	' v»')	, 5 n ( l ' J-    (6)
- z %	⎡ u	( v 2 ( l 1 )	1,6 n ( l )	⎤⎦+ z %	⎡ u	( vy	) , 7 n ( l ' J +
+ z %	⎡ u	( v 4(" )	1, 4 n ( l )	1,

ДЙ,.- , A^- .

^A l,l,k - I

^ 2,1, k -1

A j

^v) ^ 1,1, k

(l) A 2,l,k		( l ) A 2,2,k  \	/ l 1 1 1 ^2,, j - l,k	A 2j	(1) L   A 2, n , k
( l 1 A i - I,l,k		u(l) A i - I,2,k l	УУ. ! - 1.к	УУ, , , к	(1) • • A i — l,n,k
(l) H l A. k		' l ) P i ,2, k    • L	yy—l. k	I A j.	• У‘\
'°, “ m ,1, k		' l ) H m ,2, k	A (1 ) A m , j — l ,k	M ^jk	L “ m , n , k

а где

z ( u ( v q ⁽ l ) ) , r n ⁽ l ) ) =

C rl ) ■ sign ( u ( ^vq⁽l ) )) ; |u ( ^v q ⁽ l ) )| >  r y 2 l ) ,

=* в Г¹ > . u ( v q ^{( l} > ) ;| u ( v q ^{( l} >  )| <  ^r y2 ) , r = 4,7, v q ^{( l} ) ( l = 1, g; q = 1,4) - элемент предыдущего кадра последовательности l -го РДИ. МВП, отображающие статистические связи окрестностей двух соседних кадров последовательности l -го РДИ с фильтруемым элементом v ^ l ¹ (рис. 3), могут быть получены перемножением МВП по горизонтали ¹ П ^{( 1} ) , вертикали ² п ^{( 1 )} и по времени (между кадрами) ⁴ П ^{( 1} ) как:

5 n^{( l} ) = ¹ n^{( l} ) • ⁴ n^{( l} ) ⁶ n^{( l} ) = ² n^{( l} ) • ⁴ n^{( l} ) ⁷ n ^{( l} ) = ¹ n ^{( l} ) • ² n ^{( l} ) • ⁴ n ^{( l} )

Результаты исследования

На основе оптимальных уравнений, полученных в [1-2], и квазиоптимальных уравнений (4; 6) были синтезированы и исследованы на ЭВМ устройства фильтрации статических и динамических 8-разрядных ЦПИ.

а

б

в

г

д

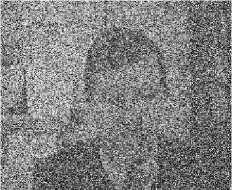
Рис. 4. Оптимальная (д, е) и квазиоптимальная (в, г) фильтрация реальных ЦПИ

е

На рис. 4 приведено исходное ЦПИ (а), зашумленное (б) при отношении сигнал-шум по мощности p 2 =-10 дБ, обработанное оптимальными (д, е) и квазиоптимальными (в, г) устройствами фильтрации.

На рис. 5 представлены графики выигрышей фильтрации по мощности сигнала η в зависимости от отношения сигнал/шум по мощности p 2 на входе фильтра при использовании оптимальных [1-2] и квазиоптимальных (4)-(6) алгоритмов. Обработке подвергались искусственные 8-разрядные полутоновые изображения размером 512×512, сформированные на основе ММ ЦПИ [3]. Выигрыш вычислялся суммированием выигрышей, полученных для каждого РДИ:

n = ^^>^ i0lg (рВЫх /р2) дБ, где Р(вЫх — отношение сигнал/шум в l-ом РДИ на выходе нелинейного фильтра.

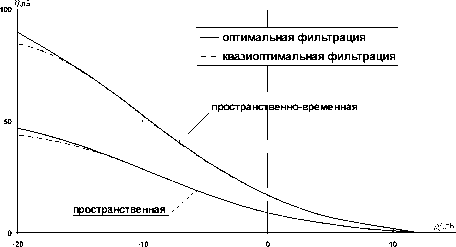
Рис. 5. Зависимость выигрыша фильтрации от отношения сигнал-шум по мощности на входе фильтра.

В таблицах выполнено сравнение вычислительной сложности оптимальных и квазиопти-мальных алгоритмов, рассмотренных в данной работе. В таблице 1 представлено количество операций вычисления, требуемое для обработки одного кадра g-разрядной последовательности ЦПИ размером m х n каждым из методов. Сложность вычисления экспоненциальной функции приравнивалась к четырем операциям умножения.

В таблице 2 приведены ресурсы памяти, необходимые для обработки одного кадра g –разрядной последовательности ЦПИ размером m х n каждым из методов. Для расчетов принимается, что для хранения любой переменной требуется 2 байта (Б) памяти.

Память, необходимая для оперативного хранения значений апостериорных вероятностей (всех элементов предыдущей строки, предыдущего элемента текущей строки, фильтруемого элемен- та, при межкадровой фильтрации еще и всех элементов предыдущего кадра), обозначена Sопер и для внутрикадровой и межкадровой фильтрации соответственно равна:

5_onep=2j» g + g + l)E – для пространственной (внутрикадровой) фильтрации,

^onep = ² (™ ¹¹ S + П g + g+l)B – для пространственно-временной (межкадровой) фильтрации.

Таблица 1. Вычислительная сложность

алгоритм фильтрации	количество математических операций
	сложение	умножение
оптимальный межкадровый	42 m n g	8 4 m n g
оптимальный внутрикадровый	1 8 in n g	3 6 m n g
квазиоптимальный межкадровый	7 m n g	< 7 m n g
квазиоптимальный внутрикадровый	3 m n g	< 3 in n g

Таблица 2. Объем используемой памяти

алгоритм фильтрации	требуемые ресурсы памяти
оптимальный межкадровый	(28g)E + Sonep
оптимальный внутрикадровый	(12g)B + Sonep
квазиоптимальный межкадровый	(42g)E + S„„cp
квазиоптимальный внутрикадровый	(18g)B + Soncp

Использование предложенных аппроксимаций нелинейной функции позволяет существенно снизить вычислительную сложность алгоритмов обработки изображений [1-2] без заметных потерь в качестве фильтрации в широком диапазоне допустимых отношений сигнал-шум на входе приемного устройства. Структура уравнений квазиоптимальной фильтрации (4)-(6) обладает высокой однородностью, что позволяет получить достаточно простые в реализации устройства фильтрации ЦПИ.