Квазипериодические оптические элементы

В настоящей работе рассматриваются фазовые оптические элементы с периодической или близкой к ней структурой. Периодичность структуры дифракционной решетки обусловливает целый ряд ее специфичных свойств. В работе []] были рассмотрены возможности манипулирования свойствами фазовой дифракционной решетки путем воздействия на структуру ее периода (фазовой функции). Здесь мы рассмотрим некоторые дополнительные возможности управления свойствами дифракционной решетки за счет согласования фазовых функций последовательных периодов решетки, то есть создания квазипериодических структур.

Закон, по которому согласовывают фазовые функции периодов решетки, обычно задается с помощью другой фазовой функции с большей областью определения. Таким образом, имеет место модификация быстропериодической фазовой функции с помощью медленно меняющейся апериодической или длиннопериодической фазовой функции. По-видимому, первым историческим примером такого рода действий с дифракционной решеткой были предложенные еще Роулендом изогнутые дифракционные решетки. Можно найти некоторые аналоги и среди сверхрешеток.

Падающее на элемент световое поле - монохроматический когерентный пучок лазерного излучения в виде плоской или сходящейся сферической волны, Период решетки предполагается достаточно большим, так что поляризация не учитывается. Под спектром решетки мы понимаем распределение энергии дифрагированного поля по плоским волнам для случая падения на решетку плоской волны, а также распределение энергии в фокальной плоскости для случая радения на решетку сходящейся сферической волны.

1. Решетки с "непрерывным" спектром

Фокальная картина (распределение интенсивности в спектре) практически не зависит от распределения интенсивности падающего на элемент излучения, если пучок падает на достаточно большое число периодов (то есть период много меньше размера падающего пучка) .

Данное свойство дифракционной решетки - устойчивость фокальной картины к изменениям распределения интенсивности в падающем пучке - обусловлено многократным повторением со сдвигом фазовой функции одного периода решетки, но в то же время это повторение приводит к тому, что фокальная картина, создаваемая одним периодом при наличии многих периодов, распадается на ряд пятен, отношение размера которых к расстоянию между ними равно числу периодов.

Это значит, что получить непрерывную фокальную картину, например, в виде линии или заданного распределения интенсивности в некоторой плоской области, путем простого повторения со сдвигом фазовой функции фокусирующего элемента невозможно.

Для решения поставленной задачи предлагается повторять со сдвигом фазовую функцию фокусирующего элемента необходимое число раз, но при этом дополнительно вводить при каждом повторении постоянные фазовые сдвиги таким образом, чтобы фокальная картина оставалась непрерывной (такой же, как и без повторения) и распределение интенсивности в ней не изменялось.

Распад фокальной картины на пятна при наличии многих периодов (повторяющихся участков) физически обусловлен когерентной интерференцией световых полей, дифрагированных различными периодами. Этот распад математически описывается умножением комплексной амплитуды с(и), описывающей фокальную картину на модулирующую функцию, имеющую переменную амплитуду. Если создать между периодами дополнительные фазовые сдвиги, то эту модулирующую функцию можно сделать постоянной по модулю. Тогда модулируется только фаза величины с(и), а интенсивность фокальной картины I(u) = |c(u)|2 остается такой же, как при наличии только одного периода. Когерентная интерференция пучков света от различных периодов не исчезает, но в фокальной плоскости влияет только на фазу, но не на интенсивность.

Покажем, как находить нужные величины фазовых сдвигов. Рассмотрим одиночный Фокусирующий элемент с фазовой функцией f(х), где 0 < х £ d. Для сходящегося пучка лазерного излучения с равномерным распределением интенсивности в пучке фокальная картина распределения интенсивности описывается коэффициентами Фурье, соответствующим главным направлениям дифракции:

- -2mnx/d 1f(х > с = / е             е

(1.1)

п о

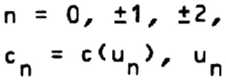
nXf d

где

• X - длина волны света;

• f - фокальное расстояние;

• и - пространственная координата в фокальной плоскости.

Распределение амплитуды с(и) полностью определяется величинами с^, то есть своими значениями в точках и , а между ними оно интерполируется siпс-функцией. п

Если повторить функцию f(x) (с фазовым сдвигом р^ при k-ом повторении) N раз, то период станет в N раз больше и каждый интервал (un, un+i^ разделится на N подинтервалов; при этом интерполирующая функция на точках, разделяющих эти интервалы, описывается дискретным преобразованием Фурье вида:

а = 1 "l' e-2nikm/N e'pk m = 0 1 2,...,N-1.                           (1.2)

• ^{m N} к = 0

Если все р^ = 0, то это даст ат = 0 при т#0 - распад фокальной картины на отдельные пятна, тем меньшего размера, чем больше N. Но можно найти такие р^, что |ат1 = 1 при т = 0,1,2,...,N-1, то есть фокальная картина останется непрерывной, с прежним распределением интенсивности (вместо амплитудной модуляции в фокальной картине будет лишь фазовая).

Покажем, что для четных N есть решение, описываемое простой формулой:

Pk = nk3/N, N = 2L,                                                             (1.3)

тогда имеем

N-1

Е к = 0

-2ni(km-к3/2)/ N е

1 N"1   - j^t-Ck-m)2 *ш2]

= - Е е

N к = 0

,  _ .

1      2n-1 2m —yr---

1 -nm /N „

— e      Ее

Числа k-m пробегают величины -m,...,(N-1)-m . Их можно рассматривать как остатки (вычеты) по модулю N, к некоторым из которых добавлено -N. Но

(k-N)2 = к2 + № - 2Nk = к2 - 2Nk + 2NL = к2 ♦ 2N(L-k) = к2 mod(2N).

Это значит, что числа в фигурных скобках под знаком суммы лишь переставляются, а сама сумма не меняется при разных т. Для нечетного N можно найти величины р^ численным расчетом.

Все сказанное для повторения вдоль оси координат х независимо справедливо и для повторения вдоль оси координат у. При этом мы получаем квазипериодический фазовый фокусирующий элемент,устойчивый к сдвигам по обеим осям координат и нестабильности падающего пучка с формулой для фазовых сдвигов

(N)

(М) .

р mzn

Pm * Р т

п

где М, N - четный, имеющий "непрерывный" спектр.

• 2, Произведения бинарных решеток

Бинарные дифракционные решетки отличаются тем, что их фазовая функция принимает только два значения. Благодаря этому они наиболее технологичны, то есть просты в массовом производстве, основой которого является литография. В данном разделе мы рассмотрим те методы модификации фазовой функции таких решеток, при которой решетка остается бинарной.

Одним из таких методов является сложение двух бинарных фазовых функций. Если каждая из них принимает значения только 0 и п, то их сумма может принимать значения 0, п, 2п; но 2тс для фазовых функций тождественно 0. Сложению фазовых функций пропускания (функций, на которые умножается падающее когерентное поле, записанное в комплексной форме, при прохождении решетки). Поэтому решетку, полученную таким образом из двух фазовых функций, естественно называть их произведением.

Рассмотрим один период фазовой дифракционной решетки с фазовой функцией <р(х), О 2 х 2 d. Спектр решетки определяется амплитудами, соответствующими главным направлениям дифракции, - амплитудами дифракционных порядков:

а = d’1 / e"2ninx/d е'^’^ dx, n = 0, 11, 12,...                      (2.1)

П          о

Для второй решетки с фазовой функцией фСх), 0 < х < Q соответствующие амплитуды обозначим b . п

Предположим сначала, что d = D. С помощью (2.1) можно записать ряды Фурье для функции пропускания решетки:

• f, = е^1*’ =  " a e2ninx/d, 1, = е1ф<Х> =  = ь e2n1nx/d

П=-оо П                                    П = -«> е                                                              ,    , , (фСх) тфСх)

Если рассмотреть решетку с функцией пропускания т = т1тз = ее

"произведение" решеток, то для нее коэффициенты ряда Фурье можно получить по формуле:

с = d-* / eiQ

= d4 / (Е a e^n^mx^d)(E b, e2nikx/d) e-2ninx/d

(2.3)

- г г              (m+k-n)x/d

= d J E a„bLedx = o । m к m,k=-”

= d-^ E a b. m+k=h m k в согласии с известной теоремой о свертке.

Формулу (2.3) трудно использовать непосредственно для построения решетки с какой-либо конкретной формой спектра. Единственным исключением, пожалуй, являет- ся построение решетки с большим количеством подряд идущих порядков одинаковой энергии и с близкой к нулю энергией во всех остальных порядках,

Как известно, для решения этой задачи нужно решать систему нелинейных алгебраических уравнений, размерность которых определяется числом порядков с равной энергией. При большой размерности решение найти сложно или вообще не удается (см. [2]) .

В этом случае можно воспользоваться следующим методом. Предположим, что период первой решетки d целое число раз N укладывается в периоде второй решетки D, то есть D = Nd. Если рассматривать D как период (не минимальный) и для первой решетки, то ее спектр будет отличаться тем, что а_п = 0 при n * mN, то есть ненулевую энергию будет иметь только каждый N-й порядок дифракции, включая нулевой. Тогда, выбрав в качестве второй решетки такую, что ее спектр имеет ровно N подряд идущих порядков одинаковой энергии, а остальные близки по энергии к нулю, мы можем получить (при условии, что первая решетка того же типа имеет М равных по энергии порядков) решетку, которая имеет NM близких по энергии порядков. Можно даже взять в качестве второй решетки ту же самую, но сжать ее период в N раз, тогда мы получим решетку с № порядками равной энергии.

Если точность выравнивания энергии в дифракционных порядках для получения таким методом бинарных решеток нужно улучшить, то полученные фазовые функции можно использовать как разумное начальное приближение для расчета по методу [2].

Таким образом, представляется полезным рассматривать модификацию быстропериодической фазовой функции тоже с помощью периодической, но со значительно большим периодом. В частном случае, когда на оптическом элементе помещается всего один период долгопериодической (модулирующей) фазовой функции, мы приходим к ситуации, аналогичной описанной в разд. 1 данной статьи.

Заключение

Описанные в данной статье приемы призваны служить в первую очередь для вычисления фазовых функций синтезируемых оптических элементов и позволяют в ряде случаев либо найти решение, которое трудно найти другими методами, либо придать решению (оптическому элементу) новые свойства. Это достигается за счет некоторой рациональной декомпозиции фазовой функции элемента: выделения периодической, особенно быстропериодической части. Последняя может описываться сравнительно небольшим числом параметров, но иметь высокие пространственные частоты, что затрудняет прямое решение задачи, приводя к искусственному сильному завышению размерности решаемых систем уравнений. В то же время указанная декомпозиция может помочь определить или осознать качественную роль наличия в структуре оптического элемента периодической или почти периодической структуры, иногда скрытой (неявной) , но сильно влияющей на его характеристики и особенности применения.