Квазипериодические режимы динамики в модели миграционно связанных сообществ "хищник-жертва"
Автор: Курилова Е.В., Кулаков М.П.
Журнал: Региональные проблемы @regionalnye-problemy
Рубрика: Математическое моделирование. Биология
Статья в выпуске: 2 т.23, 2020 года.
Бесплатный доступ
Изучается модель динамики неидентичных миграционно связанных сообществ «хищник - жертва» с лимитированием роста жертв и насыщением хищников. Исследуются механизмы формирования сложных пространственно-временных динамических структур, объединяющих в себе как быстрые и медленные изменения численностей, так и различные соотношения синхронной и несинхронной динамики в определенные периоды времени. Описаны сценарии перехода между разными типами пачечной динамики с периодическим изменением численности при вариации различий рассматриваемых сообществ, приводящие в итоге к квазипериодической динамике связанных сообществ.
Хищник - жертва, миграция, синхронизация, бифуркация, тонические и пачечные колебания
Короткий адрес: https://sciup.org/143173188
IDR: 143173188 | УДК: 574.34:517.925.4 | DOI: 10.31433/2618-9593-2020-23-2-3-11
Текст научной статьи Квазипериодические режимы динамики в модели миграционно связанных сообществ "хищник-жертва"
Модели, описывающие динамику биологических систем по типу «хищник – жертва», «паразит – хозяин», «ресурс – потребитель» и т. п., продолжают активно изучаться, несмотря на огромную их историю, проработанность соответствующего математического аппарата и разнообразные результаты [3]. Постоянно расширяется предметная область моделей подобного типа. Например, нависшие над человечеством пандемии мотивируют математических биологов разрабатывать и исследовать эколого-эпидемиологические модели. В этих исследованиях описывается распространение инфекции в популяциях, в которых здоровые и зараженные особи взаимодействуют по принципу «хищник – жертва» или «паразит – хозяин» [10, 12]. Независимо от предметной области, математические модели таких биологических систем построены, как правило, с использованием аппарата обыкновенных дифференциальных уравнений. Интерес вызывают сложные нелинейные явления, связанные, например, с синхронизацией динамики на разных территориях [8], механизма- ми формирования сложных пространственно-временных структур [6, 9], сложным динамическим поведением [4] и т.п.
В настоящей работе продолжено исследование модели динамики численности двух неидентичных миграционно связанных сообществ, функционирующих по принципу «хищник – жертва» с функциональным откликом Холлинга II типа [1, 2]. Каждое из сообществ представляет собой автоколебательную подсистему и описывается при помощи уравнений Базыкина [5]. В зарубежной литературе подобного рода уравнения именуются моделью Розенцвейг-Макартура [11]. Ранее были исследованы некоторые механизмы формирования сложных пространственно-временных режимов при изменении различий между рассматриваемыми сообществами [1, 2]. Эти режимы интересны тем, что сочетают в себе как периодические колебания с быстрыми всплесками численностей, так и участки медленной тонической динамики. Сложные режимы в этой модели возникают в результате частичной синхронизации рассматриваемых сообществ и отличаются раз- личным соотношением синхронной и несинхронной динамики в разные промежутки времени. В результате фазовая траектория хоть и остается периодической или квазипериодической, но оказывается устроенной довольно сложно [1].
Модель динамики двух связанных неидентичных сообществ
Данное исследование направлено на изучение двух соседних неидентичных взаимосвязанных сообществ «хищник – жертва», обитающих в схожих условиях и не имеющих существенных различий внутривидовой и межвидовой конкуренции между сообществами. Обозначим через X 1, Y 1 и X 2, Y 2 соответственно общую численность популяции жертвы и хищника в первом и втором сообществах в момент времени t . Неидентичность сообществ выражается в существенной разности максимальных скоростей воспроизводства популяции жертвы, обозначенных a 1 и a 2 соответственно. Это отражает ситуацию, когда на сопредельных территориях обитают два принципиально разных вида жертв, но имеющих одинаковую пищевую ценность для хищника. Сопредельные территории предполагают наличие миграции хищников между сообществами (далее именуемыми «подсистемами»), причем количество мигрантов с территории пропорционально численности хищников данного сообщества. Коэффициенты пропорциональности (коэффициенты миграций) одинаковы для обеих подсистем, что создает симметричную связь между сообществами. Гибель особей в процессе миграции неявно включается в общую смертность.
В результате уравнения динамики численности двух связанных сообществ «хищник – жертва» в случае лимитирования роста жертв и насыщения числа поглощенных хищниками жертв, описываемые функцией Холлинга II типа, имеют вид [1, 2]:
пуляции жертв в каждом местообитании в отсутствии хищника, B – удельная скорость потребления популяцией хищника популяции жертвы при единичной плотности обеих популяций, C – естественная смертность хищника, S/B – коэффициент переработки потребленной хищником биомассы жертвы в собственную биомассу, H – коэффициент насыщения хищника, M – коэффициент миграции хищника.
Для уменьшения числа независимых параметров будем использовать следующую замену переменных: Xi ( t )= Cxi ( τ ) /s , Yi ( t ) =Aiyi ( τ ) /b , а также характерного времени: ti=τ/Ai ( i =1, 2). В результате система уравнений (1) преобразуется к следующей системе:
x-^ = = X ] (1 - a X ])
dt 1 1
dy 1 =
dt
d x 2
dt
d y 2
dt
x 1 y 1
1 + hx 1
- c 1 y 1 +
c 1 x 1 y 1
1 + hx 1
a x 2
- c 2 y 2 +
/
c
+ c 1 m — y 2
к c 2
) _ x 2 y 2
1 + hx 2
c 2 x 2 y 2
1 + hx 2
\
y 1
(2),
c, + c 2 m — У 1 _ y 2
I c1
\
dX i = AX K - X i _ BXY
dt 11 K 1 + HX1
dYL = _ cy + SXY + m ( у _ у )
dt 1 1 + AX1
d X, , v K - X, B XY
---2- = AX-----2
dt K 1 + HX 2
dY = _су + SX2Y2 + m(у -у dt 2 1 + HX 2
где K – устойчивая равновесная численность по-
где h=HC/S – новый коэффициент насыщения хищника, a=C /( KS ) – коэффициент самолимити-рования жертвы, ci=C/Ai – относительная скорость снижения (убыли) численности хищников (смертности) и mci=M/Ai – коэффициент миграции хищников ( i =1, 2).
После предложенной замены два рассматриваемых сообщества, отличающиеся скоростями роста численности жертв, становятся подобны сообществам с разной смертностью хищников. При этом численности особей, покинувших одну территорию (эмигрантов) и прибывших на другую (иммигрантов), не совпадают, т.е. связь в системе (2) несимметрична, что указывает на смертность хищников в ходе миграции. При этом в процессе увеличения различий в смертности хищников растет диспропорция ( γ 1 /γ 2) (отлична от единицы) между числом эмигрантов и иммигрантов.
В случае отсутствия связи между рассматриваемыми сообществами ( m =0) система (2) состоит из двух независимых автоколебательных подсистем. Из области существования предельного цикла выберем следующие значения параметров: a =0.1, h =0.5. В этом случае в каждой из подсистем реализуется предельный цикл с перио-
дом, зависящим от значений параметров сi ( i =1,2). В полной системе он реализуется вокруг точек B 1 или B 2 в зависимости от начальных численностей. Кроме двух этих циклов в системе возможна пара устойчивого и неустойчивого циклов вокруг точек E 0 и E 1. Значение скорости снижения численности хищников второго сообщества примем равным с 2=0.5, подразумевая, что эта территория с низкой скоростью роста численности жертв. Учитывая переход от системы (1) к (2), можно утверждать, что это эквивалентно высокой смертности хищников. При выбранном значении параметра с 2 динамика второго сообщества имеет небольшой период колебаний по сравнению с первым, что способствует формированию короткопериодичного цикла. Низкая же скорость снижения численности хищников первого сообщества с 1=0.002 соответствует территории с высокой скоростью роста численности жертв, что эквивалентно низкой смертности хищников. При этом динамика первого сообщества приводит к образованию длиннопериодичного цикла. Для проведения численных экспериментов будем варьировать значения параметров a и c 1 в окрестности значений a =0.1, h =0.5, с 1=0.002, с 2=0.5, m =0.005, наблюдая при этом за устойчивостью всех особых точек и типом динамического поведения.
Результаты бифуркационного анализа
Система (2) имеет несколько биологически значимых особых точек: тривиальная А 0(0;0;0;0) с нулевымичисленностямивсехпопуляций,полутри-виальные А 1(1/ а ;0;0;0), А 2(0;0;1/ а ;0), А 3(1/ а ;0;1/ а ;0), B l ( ( 1 + 2 m )/ 1 , , ( 1 + m )p 2/^2 ,0, c 2 m P. /( c 1 Д 2 )) и B 2 ( 0, c m P./{c .Pi], ( 1 + 2 m )/ Д, ( 1 + m )pJp^
(P , = 1 - h + m - 2 hm , p = = Px- a - 2 am ) с нулевыми численностями одной или нескольких популяций на разных территориях, а также три нетривиальные с полностью ненулевыми численностями E i ( xc (0\ J ,0) , x 2 0) , y 20) ) ( i = 0,1,2 ). Были вычислены координаты всех точек, исследованы условиях их существования и описаны простейшие их бифуркации [1]. В частности, показано, что пара точек Е 1 и Е 2 рождается в результате седло-узловой бифуркации ( SN ) при c 1=0 (рис. 1 а ).
Характер других бифуркаций показан на рис. 1 а - б , где соответствующими линиями отмечены основные локальные бифуркации. Линия TC – это транскритическая бифуркация, в результате которой две точки Е 1 и В 1 при изменении параметров сближаются и обмениваются устойчивостью. Причем таким образом, что слева от нее устойчива точка B 1, а справа E 1. Линии H+ и H – от-
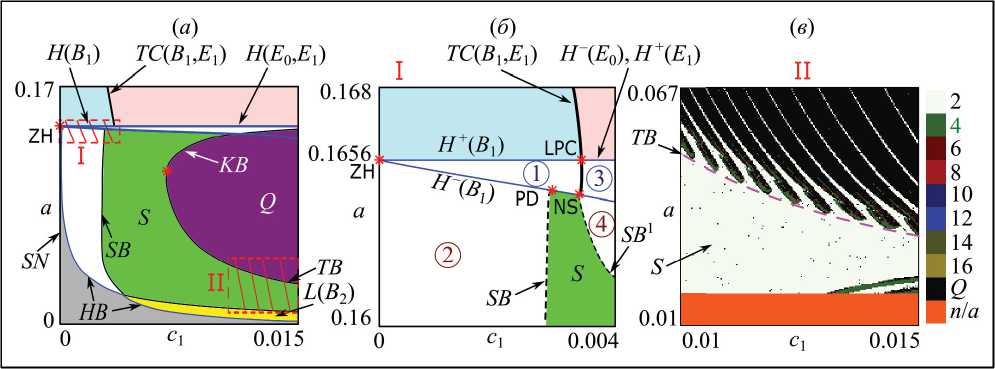
Рис. 1. (а) Бифуркационная диаграмма системы (2) и (б) ее увеличенный фрагмент в области параметров I. (в) Карта динамических режимов в области II, охватывающая область строго периодической пачечной динамики S и квазипериодической динамики Q
Fig. 1. (a) Bifurcation diagram of system (2) and (б) its enlarged fragment in the parameter area I. (в) Chart of dynamic regimes in domain II covering the domain of strictly periodic burst S and quasi-periodic dynamics Q мечают супер- и субкритическую бифуркации Ан-дронова-Хопфа, в результате которых рождаются соответственно устойчивый или неустойчивый предельные циклы вокруг отмеченных в скобках особых точек. В данном случае происходит следующая цепочка переходов между разными периодическими решениями системы (2). На линии H+(B1) и H+(E1) из точек B1 и E1 рождаются «простые» устойчивые предельные циклы в области 1 и 3 на рис. 1б. Первое периодическое решение реализуется при нулевой численности жертв на второй территории, при втором жертвы присутствуют на обеих территориях (рис. 2а). На линии TC, которая тянется из области устойчивости и пересекает линию H, эти циклы сближаются и обмениваются устойчивостью, т.е. в области 1 цикл вокруг точки B1 устойчив, вокруг E1 неустойчив, а в области 3 все наоборот. При переходе линии H–(B1) и H–(E1) эти циклы теряют устойчивость и в области 2 и 4 формируется релаксационный (быстро-медленный) предельный цикл или канард [7]. Оба этих цикла отличаются не только соотношением численностей жертв, но и, что более важно, степенью синхронизации. Примеры таких циклов показаны на рис. 2б. Несложно заметить, что в области 2 динамика хищников на обеих территориях синфазная, в то время как в области 4 динамика хищников и жертв – противофазная. Наконец при приближении к линии HB периодические решения увеличивают свой размах, период колебаний неограниченно возрастает, а сам цикл разрушает- ся вследствие гомоклинической бифуркации.
Остальные линии на рис. 1 а - б отмечают последующие бифуркации периодических режимов. На линии SB в динамике численностей хищника и жертвы появляются участки с быстрыми всплесками (пачечная динамика), чередующиеся с участками медленной (тонической) динамики, как часть релаксационного предельного цикла (рис. 3). В области S на рис. 1 а - б периоды следования быстрой и медленной динамики строго периодические, в то время как в Q периодичность нарушается и динамика оказывается квазиперио-дической.
На основе численных экспериментов можно утверждать, что области S и Q неоднородны. В первой области происходит чередование режимов, которые отличаются порядком следования быстрой пачечной части цикла относительно медленной. Например, в простейшем случае пачечная активность возможна только после стремительного роста числа жертв на первой территории. Участок с быстрой динамикой или пачка при этом имеет треугольную форму, состоящую из затухающих колебаний (рис. 3 а ). Быстрые, в этот раз, расходящиеся колебания могут возникнуть в двух случаях: при низкой численности жертв и намного раньше стремительного их роста на первой территории (рис. 3 б ) или после полного восстановления жертв первого сообщества (рис. 3 в ). Форма пачки в этом случае – усеченный ромб или ромб, которые показаны на рис. 3 б и 3 в соответственно.
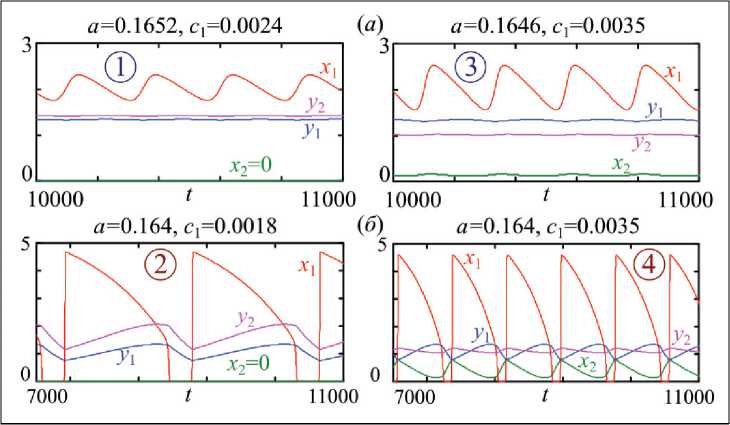
Рис. 2. Примеры динамики в системе (2) из областей 1-4 на рис. 1б: (а) предельный и (б) быстро-медленный цикл (канард)
Fig. 2. Examples of dynamics in system (2) from domains 1–4 in Fig. 1б: (а) limit cycle and fast- slow cycle (canard)
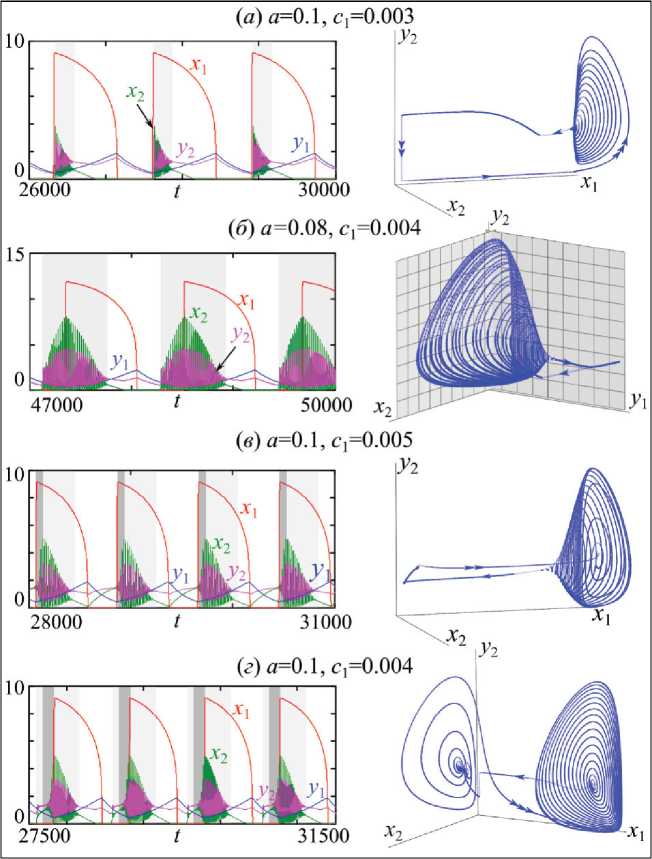
Рис. 3. Примеры пачечной динамики в системе (2) из области S, которые отличаются формой пачек и видом аттракторов
Fig. 3. Examples of burst dynamics in a system (2) from domain S which differ in the shape of spike clusters and the type of attractors
Динамика в обоих случаях сочетает в себе расходящиеся и затухающие колебания численностей.
Более подробное исследование разных типов динамики в системе (2), а также описание разных видов пачек и механизмов их возникновения было приведено в [1]. Помимо описанных выше режимов в области S возможны более экзотические формы пачек, состоящие из последовательности затухающих, расходящихся и вновь затухающих быстрых колебаний численностей. Пример такой динамики показан на рис. 3г. В этом случае затухающие колебания небольшой амплитуды возникают после скачка численности жертв второго сообщества при минимальных значениях пер- вого (равных 10–6–10–9). Эти колебания сменяются раскачивающимися, что приводит к более активному перемещению хищников с соседней территории. Необходимо отметить, что данный период времени (возникновение и переход от одного вида колебаний к другому) характеризуется превышением числа хищников над численностью жертв второго сообщества. Одновременно с достижением раскачивающихся колебаний максимальной амплитуды в пачке происходит взрывной всплеск численностей жертв на первой территории. Раскачивающие колебания вновь сменяются затухающими, а число жертв падает вследствие более интенсивного их поедания. Изменения численно- сти хищников в первом сообществе синхронны колебаниям числа жертв на данной территории. Популяция жертв второго сообщества при этом восстанавливается раньше, чем на первой территории, что приводит к более раннему выходу на пачечный режим и увеличению размера пачки, т.е. растет число витков вокруг нетривиальной точки. Таким образом, хищники второго сообщества в период малого числа жертв остаются на своей территории, а их численность восполняется за счет миграции с сопредельной территории ввиду отсутствия там жертв. Численность хищников первого сообщества не изменяется, они находятся на своей территории до почти полного уничтожения жертв, после чего перемещаются на соседнюю территорию и участвуют в поедании жертвы уже второго сообщества до момента взрывного увеличения численности жертв на своей территории.
Описанные циклы из области S , помимо описанных выше динамических особенностей, отличаются количеством витков на быстром пачечном многообразии – их число растет по мере приближения к области квазипериодической динамики Q . Рассмотрим область квазипериодиче-ской динамики Q , в которой режимы с бесконечно большим периодом чередуются с резонансными циклами с конечным периодом в соответствии со сценарием Неймарка-Сакера или буфуркацией разрушения тора (рис. 1 в ).
Исследование квазипериодической динамики Чтобы более детально изучить неоднородность области Q, построим сечение Пуанкаре к траектории системы (2). В качестве секущей выберем плоскость, проходящую через полутриви-альную точку B 1 и параллельную координатным осям. В этом случае уравнение такой плоскости имеет вид:
L 1 + 2 m 1
я = i( x i ,У 1, x 2, y 2) e R x i = x B =■:—;-------—r-
[ 1 1 - h + m - 2 h m
Несложно заметить, что вид этой секущей плоскости не зависит от варьируемых параметров a и c1, и поэтому ее положение фиксированное (в данном случае xB=2.02). Но более важно, что она расположена строго между двумя ветвями быстрого пачечного многообразия таким образом, что модельная траектория пересекает плоскость π только лишь в медленной тонической части цикла. В результате для режимов из области S траектория, очевидно, пересечет плоскость π лишь в двух точках независимо от количества полных оборотов цикла, т.е. потребуется один виток, чтобы периодическая траектория вернулась в ту же самую точку на плоскости π. В это же время в области ква-зипериодической динамики траектория пересечет плоскость π в значительно большем числе точек (при t ^ да, как правило, в бесконечно большом). Подсчитав количество этих точек, т.е. решений системы (2), для которых |x1 - xB| <£ (е - малое положительное число), можно построить карту динамических режимов (рис. 1в). В результате на карте, изображенной на рис. 1в, цветом закодировано количество витков, необходимых для того, чтобы траектория вернулась в ту же точку фазового пространства, или, другими словами, это число равно периоду соответствующего отображения Пуанкаре (отображение последования). На этой карте хорошо видно, что область Q неоднородна. В ней чередуются области квазипериодической динамики (отмеченные черным цветом) и тонкие языки синхронизации – строго периодическая динамика (отмеченные цветом). Ведущими циклами отображения Пуанкаре являются колебания с периодом 4 и 6. Это означает, что для параметров, взятых на языке синхронизации, траектория часто содержит два или три витка. Для квазипериодиче-ской динамики траектория никогда не проходит дважды через одну и ту же точку, что на секущей плоскости отображается в виде множества точек на двумерной плоскости (рис. 4).
На рис. 4 показаны примеры аттракторов, формируемых в отображении последования на плоскости ( x 2, y 2), а также в полной системе (2). В первых двух примерах модельные параметры выбраны из области Q ближе к линии KB , в последующих примерах ближе к линии TB на рис. 1 а . Слева на рис. 4 а показаны две замкнутые инвариантные кривые, которые при небольшой вариации параметров разрушаются вблизи резонансного цикла. В результате формируется двухкомпонентный аттрактор, изображенный справа на рис. 4 а . Он состоит из 20 участков (полос). В данных двух примерах траектория системы (2) целиком лежит на бутылке Клейна ( KB ) – неориентируемой (односторонней) поверхности. Как известно, в трехмерном евклидовом пространстве эта поверхность имеет отверстие, соответствующее самопересечению на одной из стенок (внутреннее горлышко), где происходит переход с внешней части бутылки на внутреннюю (внешнее горлышко). В четырехмерном фазовом пространстве системы (2) такого отверстия нет, однако поверхность по-прежнему неориентируемая. В результате переход с внешней
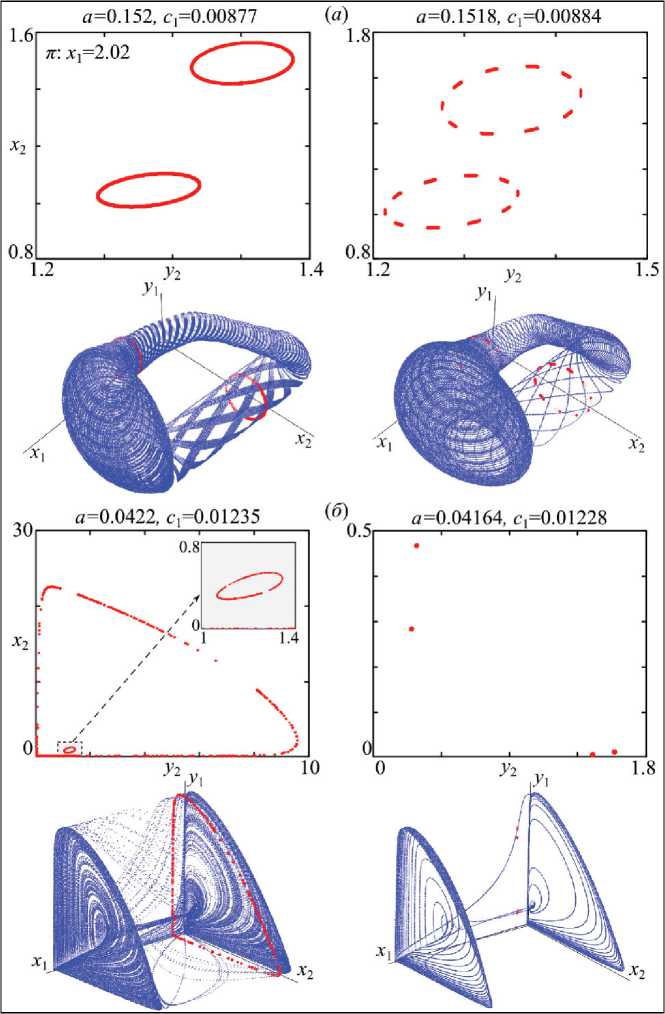
Рис. 4. Сечения Пуанкаре (верхний ряд) и аттрактор системы (2) в случае, когда траектория покрывает (а) бутылку Клейна и (б) тор
Fig. 4. Poincaré sections (upper row) and attractor of system (2) in the cases when the trajectory lies on (а) the Klein bottle and (б) the torus части бутылки на внутреннюю в модели (2) соответствует скачку численности жертв на первой территории и резко возросшей амплитуде колебаний численности жертв на второй территории. Во втором случае траектория лежит на торе (TB) – ориентируемой (двухсторонней) поверхности, формируемой за счет периодических колебаний обоих сообществ с частотами, отношение кото- рых равно иррациональному числу. В этом случае колебания численностей на обеих территориях более независимы (несинхронные). Кроме того, на тип динамики в системе (2) указывает вид инвариантных кривых в отображении Пуанкаре. В случае бутылки Клейна эти кривые расположены достаточно далеко друг от друга, как на рис. 4а. Для тора инвариантные кривые вложены друг в друга, как на рис. 4б слева (вторая инвариантная кривая небольшая и прижата к оси абсцисс). Справа этот цикл проходит через сильный резонанс (отношение частот – рациональное число 1/2) и в сечении оказывается лишь 4 точки.
Заключение
В ходе проведенного исследования системы двух неидентичных взаимосвязанных сообществ «хищник – жертва» обнаружено, что небольшие значения коэффициентов миграции m и самоли-митирования жертвы a способствуют возникновению квазипериодических режимов динамики, соответствующих потере синхронизации динамики сообществ. Этому предшествует формирование быстро-медленного цикла при низких значениях убыли хищников первого сообщества. По мере роста смертности хищника формируется пачечная динамика, которая содержит участки с медленной и быстрой динамикой. Динамика в этом случае строго периодическая и, как правило, противофазная на разных территориях. Обнаружено несколько вариантов следования быстрых и медленных колебаний, которые отличаются формой участка с быстрой пачечной динамикой (треугольная, ромбовидная и усеченная ромбовидная пачка) и соотношениями численности хищников и жертв на сопредельных территориях. Описан новый вид пачек более сложной формы, содержащих в себе последовательное чередование затухающих, расходящихся и вновь затухающих быстрых колебаний численностей.
Установлено, что модельная траектория исследуемой модели покрывает такие топологические структуры, как бутылка Клейна и тор. Показано, что для периодической динамики траектория движется по ним единственно возможным образом независимо от формы пачек, т.е. возвращается за один полный оборот в исходную точку на данных множествах. Найден диапазон параметров, в котором траектория плотно обвивает эти структуры, а динамика оказывается квазипериодической и несинхронной на разных территориях. В результате анализа этой динамики было обнаружено множество языков синхронизации. Показано, что в соответствующем отображении Пуанкаре ведущими являются 4- и 6-циклы. Это означает, что на языках траектория делает 2 или 3 полных витка на отмеченных топологических структурах.
Работа выполнена в рамках государственного задания Института комплексного анализа региональных проблем ДВО РАН и частичной финансовой поддержке РФФИ (проект № 18-51-45004 ИНД_а).
Список литературы Квазипериодические режимы динамики в модели миграционно связанных сообществ "хищник-жертва"
- Кулаков М.П., Курилова Е.В., Фрисман Е.Я. Синхронизация, тоническая и пачечная динамика в модели двух сообществ "хищник-жертва", связанных миграциями хищника. // Математическая биология и биоинформатика. 2019. Т. 14, № 2. С. 588-611 DOI: 10.17537/2019.14.588
- Курилова Е.В., Кулаков М.П., Фрисман Е.Я. Последствия синхронизации колебаний численностей в двух взаимодействующих сообществах типа "хищник - жертва" при насыщении хищника и лимитировании численности жертвы // Информатика и системы управления. 2015. Т. 45, № 3. С. 24-34
- Фрисман Е.Я., Кулаков М.П., Ревуцкая О.Л., Жданова О.Л., Неверова Г.П. Основные направления и обзор современного состояния исследований динамики структурированных и взаимодействующих популяций. // Компьютерные исследования и моделирование. 2019. Т. 11, № 1. С. 119-151 DOI: 10.20537/2076-7633-2019-11-1-119-151
- Bakhanova Y.V., Kazakov A.O., Korotkov A.G., Levanova T.A., Osipov G.V. Spiral attractors as the root of a new type of "bursting activity" in the Rosenzweig-MacArthur model. // Eur. Phys. J. Special. 2018. Vol. 227. P. 959-970 DOI: 10.1140/epjst/e2018-800025-6
- Bazykin A.D. Nonlinear Dynamics of Interacting Populations / Ed. by Alexander I. Khibnik and Bernd Krauskopf. - World Scientific Publishing Co. Pte. Ltd. 1998. 216 p. DOI 10.1142/2284
- Comins H.N., Hassell M.P., May R.M. The spatial dynamics of host-parasitoid systems. 10.2307/5627 // J. Animal Ecology. 1992. Vol. 61. P. 735-748
- DOI: 10.2307/5627//J.AnimalEcology.1992.Vol.61.P.735-748
- Ersöz E.K., Desroches M., Mirasso C.R., Rodrigues S. Anticipation via canards in excitable systems. // Chaos. 2019. Vol. 013111, N. 29
- DOI: 10.1063/1.5050018
- Goldwyn E.E., Hastings A. When can dispersal synchronize populations? // Theoretical Population Biology. 2008. Vol. 73, No. 3. P. 395-402
- DOI: 10.1016/j.tpb.2007.11.012
- Huang T., Zhang H. Bifurcation, chaos and pattern formation in a space-and time-discrete predator-prey system. // Chaos, Solitons & Fractals. 2016. Vol. 91. P. 92-107.
- DOI: 10.1016/j.chaos.2016.05.009
- Mukhopadhyay B., Bhattacharyya R. Role of predator switching in an eco-epidemiological model with disease in the prey. // Ecological Modelling. 2009. Vol. 220, No. 7. P. 931-939
- DOI: 10.1016/j.ecolmodel.2009.01.016
- Rinaldi S., Muratori S. Slow-fast limit cycles in predator-prey models. // Ecological Modelling. 1992. Vol. 61. P. 287-308
- DOI: 10.1016/0304-3800(92)90023-8
- Saifuddin Md., Biswas S., Samanta S., Sarkar S., Chattopadhyay J. Complex dynamics of an eco-epidemiological model with different competition coefficients and weak Allee in the predator. // Chaos, Solitons & Fractals. 2016. Vol. 91. P. 270-285
- DOI: 10.1016/j.chaos.2016.06.009


