Квазипластичное удаление поверхностного слоя твердых хрупких материалов с получением нанометрового рельефа поверхности

Среди полезных ископаемых в последнее время все большее применение в различных отраслях промышленности находят минералы. Кроме традиционных сфер применения в строительстве и ювелирной промышленности, минералы, особенно в форме кристаллических образований (кристаллов), находят широкое применение при производстве высокотехнологичных изделий в области нанотехнологий. Расширение области применения минералов (в том числе кристаллов) ставит задачу их поверхностной обработки с получением заданных выходных параметров для различных сфер применения. Технологический процесс формообразования поверхности при обработке минералов можно рассматривать как процесс удаления поверхностного слоя материала с формированием поверхности заданной шероховатости и неплоскостности. Особое значение приобретает качество обработки поверхности с минимизацией отходов сырья для применения кристаллической формы минералов, в том числе алмаза и лейкосапфира, в микроэлектронике при    изготовлении подложек интегральных микросхем (ИМС). В настоящее время полупроводниковые схемы на лейкосапфировых подложках изготавливаются с применением эпитаксии. Эпитаксия — это метод послойного выращивания одного кристаллического твердого тела на поверхности другого (называемого подложкой),    при    котором    растущий    кристалл    наследует кристаллографическую структуру подложки. Подложка, изготовленная из кристаллов (кремния, лейкосапфира, алмаза и других твердых материалов), выполняет роль механического носителя и отводит тепло от микросхемы в процессе её работы. Поэтому для изготовления подложек применяются кристаллические материалы, обладающие большой твердостью и высокой теплопроводностью (лейкосапфир, алмаз). В настоящее время формирование поверхности нанометрового рельефа для последующего этапа эпитаксии таких материалов является большой проблемой. Качество поверхностного слоя подложек существенно влияет на структурное совершенство эпитаксиального слоя. Дислокации и дефекты поверхностного слоя формируются и зависят от подложки и наследуют её отрицательные свойства, ухудшая эксплуатационные свойства микросхем. В этих условиях при поверхностной обработке материалов на первый план выходит вопрос недопустимости возникновения сколов, трещин, микродефектов и дислокаций в основной массе материала. Требуется получение нанометрового рельефа поверхности с минимальным количеством дефектов, привнесенных процессом обработки. Для выполнения требований необходимо прецизионное удаление поверхностного слоя материала. Это особенно актуально для получения поверхности нанометрового рельефа, шероховатость которого соизмерима с параметрами кристаллической решетки обрабатываемого материала.

Традиционным способом обработки твердых хрупких материалов и кристаллов является механическое шлифование свободным и связанным абразивом. После такой обработки получается поверхность с шероховатостью около 200 нм и нарушенным подповерхностным слоем. Для достижения необходимой шероховатости (например, для лейкосапфира 0,2 нм) при изготовлении подложек заготовка полируется в агрессивных средах.

Перспективным способом получения высококачественной поверхности твердых хрупких кристаллических материалов нанометрового рельефа является удаление поверхностного слоя в режиме квазипастичности [1]. Квазипластичность – проявление пластичных свойств поверхностным слоем твердых хрупких материалов при обработке. Технология квазипластичной обработки твердых материалов основана на обеспечении механического воздействия на обрабатываемую поверхность (ОП) материала при подаче шлифовального круга (ШК), составляющей доли мкм/ход. При этом поверхностный слой хрупких твердых материалов проявляет пластичные свойства и преобладающим механизмом становится не хрупкое разрушение, а квазипластичное удаление поверхностного слоя материала. При данных подачах контактное взаимодействие зерен шлифовального круга с обрабатываемой поверхностью создает периодическое переменное механическое поле, под воздействием которого происходит направленное квазипластичное удаление поверхностного слоя с формированием поверхности нанометровой шероховатости и с минимальными дефектами (не более 50 нм), внесенных процессом обработки.

При квазипластичной обработке можно проводить постоянный контроль процесса обработки, на основе которого автоматизировать процесс поверхностной обработки. В результате появляется возможность получения большого количества изделий из твердых хрупких материалов (в том числе кристаллов) со стабильным качеством поверхностного слоя нанометровой шероховатости.

Впервые процесс обработки в режиме квазипластичности был исследован Т.Г. Бифано и Т.А. Доу в восьмидесятых годах двадцатого века на установке «PEGASUS» [2]. В результате проведенных экспериментов на большом количестве аморфных стекол, монокристаллов и керамических материалов авторами были установлены условия хрупко-пластичного перехода, при котором все материалы, независимо от их твердости и хрупкости, в процессе механической поверхностной обработки претерпевают переход от хрупкого режима разрушения к квазипластическому. В продолжении этих работ на основе работ академика Панина В.И. д.т.н. Сильченко О.Б. и к.т.н. Коньшиным А.С. созданы теория и методы размернорегулируемой и бездефектной обработки твердоструктурных минералов [3]. Под руководством к.т.н. Коньшина А.С. на основе фундаментальных работ д.т.н., проф. Кудинова В.А., д.т.н., проф. Ратмирова В,А., д.т.н., проф. Левина А.И., к.т.н. Бобрина В.И. в ЭНИМСе был создан станочный модуль АН15ф4 с числовым программным управлением (ЧПУ). Основные параметры станочного модуля приведены в таблице 1.

Таблица 1.

Параметры станочного модуля АН15ф4

Параметр	Величина
Число управляемых осей	6
Число позиций для установки режущего инструмента и контрольно-измерительных средств (револьверная головка)	3
Число шпинделей	3
Дискретность задания и отработки перемещений - оси X, Y , мкм -  - ось Z, мкм – -    оси А, В, град.	0,05 0,05-0,03 0.0001
Максимальная величина перемещений -    линейная ось X, мм -    линейная ось Y, мм -    линейная ось Z, мм -    круговая ось А, град. -    круговая ось В, град.	1000 300 10 90 неогранич.
Диапазон рабочих подач, мм/мин	0,06…4500
Диапазон частоты вращения шпинделей, об/мин	3000-6000
Количество мест в сменной кассете, шт.	15
Число одновременно обрабатываемых изделий, шт.	5
Шероховатость обработанной поверхности Rz, мкм	0.032...0.05
Диаметр алмазного инструмента, мм	250
Суммарная подводимая мощность, кВт	7

Основные направления движения частей упругой обрабатывающей системы (УОС) станочного модуля приведены на рис. 1

Рис 1. Основные направления движения частей УОС станочного модуля АН15ф4

При испытании макетного образца станочного модуля с ЧПУ получены положительные результаты при обработке керамических видеоголовок, изделий из сапфира, фианита, поликристаллических и натуральных алмазов, ориентированных в твердом направлении.

Удаление поверхностного слоя материала в режиме квазипластичности достигается при обеспечении жесткости конструкции упругой обрабатывающей системы и относительной изоляции от внешних возмущений. В результате заготовки из хрупких материалов можно механически обрабатывать в регулируемом режиме с получением обработанной поверхности нанометрового рельефа.

Теоретические исследования и анализ экспериментальных исследований квазипластичного удаления поверхностного слоя при обработке различных твердых хрупких материалов позволили составить классификацию состояния поверхностного слоя материала при его механической обработке по величине удельной энергии воздействия и физико - математическую модель квазипластичного удаления поверхностного слоя при прецизионной обработке твердых хрупких кристаллических минералов.

Научно-методические подходы формирования физико-математической модели основывались на корректности оценки предельных параметров напряженно-деформируемого состояния, используемых для решения задач хрупкого разрушения, включая использование критериев прочности и пластичности анизотропных твердых тел, элементов теории дислокации, основных положений термодинамики и физической мезомеханики. Физическая мезомеханика исследует вопросы, находящиеся на стыке физики твердого тела и механики деформируемого твердого тела. Применяющийся в физической мезомеханике термин “масштабные уровни деформации” предполагает четкую классификацию размеров в иерархии масштабов: микро, мезо и макро. Термин “мезоскопический” в физической мезомеханике отражает смысл “промежуточный” между твердым телом как сплошной средой и его конкретной кристаллической решеткой. При рассмотрении объекта исследования малой величины (примерно 0,5 -0,05 нм) допускается применение как элементов классических уравнений напряженно -деформируемых состояний механики сплошной среды, так и элементов теории дислокаций. Физическая мезомеханика рассматривает поверхностного слоя в нагруженных материалах как самостоятельный мезоскопический структурный уровень деформации, который имеет более высокую концентрацию дефектов и пониженный предел сдвиговой устойчивости, по сравнению с основным объемом материала.

Рассмотрим суть механизма взаимодействия алмазных зерен шлифовального круга с обрабатываемой поверхностью твердого хрупкого минерала, обладающего микронеровностиями, при поверхностной обработке минерала. Во время упругого взаимодействия выступов, согласно релаксационной модели мезомеханики, любая точка в деформируемом твердом теле испытывает сдвиг. В точке соприкосновения выступов шлифовального круга и обрабатываемой поверхности кристаллического минерала происходит локальная потеря сдвиговой устойчивости кристаллической решетки. Происходит движение дефектов в кристалле, в результате которого первоначальный концентратор напряжений релаксирует, и распределение напряжений в кристалле становится более однородным. Исходный высокопрочный кристалл в ходе квазипластической деформации наполняется дефектами структуры. Кристалл снижает свою прочность, но сохраняет сплошность. Сдвиг на микроуровне сопровождается поворотными деформациями на мезоскопическом масштабном уровне. На мезоуровне носителями квазипластического течения являются структурные элементы – мезообъемы. Формирование движущихся в релаксационном режиме мезообъемов происходит в основном в поверхностном слое обрабатываемого минерала, имеющем большую дефектность, в направлении максимальных касательных напряжений. Релаксация одних напряжений в процессе возвратно-поворотных колебаний сопровождается генерацией других внутренних напряжений. Режим квазипластичного удаления поверхностного слоя хрупких минералов можно обеспечить при специальном подборе таких параметров, как усилие прижима и скорости движения инструмента параллельно поверхности кристалла, подвергаемой механическому воздействию.

При снижении контактных напряжений величина энергии воздействия может быть недостаточна для проявления пластичных свойств хрупких кристаллов, обусловленных движением дислокаций, если напряжения меньше предела Пайерлса (тп ), соответствующего началу движения дислокаций. Режим квазипластичного удаления поверхностного слоя должен лежать в диапазоне энергий, превышающих энергию воздействия, соответствующую пределу Пайерлса, и быть меньше величины энергии, соответствующей хрупкому разрушению (определяемой, например, Ржевским В. В., Новиком Г.Я.). С учетом вышеизложенного сформирована классификация энергетического воздействия, позволяющая распределять эффекты, возникающие в поверхностном слое твердого минерала при механическом воздействии (табл. 2).

Таблица 2.

Классификация энергетических уровней состояния поверхностного слоя минералов при механическом воздействии

Состояние поверхностного слоя твердого минерала при механическом воздействии	Диапазон удельной величины энергии воздействия, W, Дж^м -3
При механической  обработке хрупкое разрушение	2 W >  σ p 2 ⋅ E
Режим «квазипластичности»	22 τ n  <  W <  p 2 ⋅ E       2 ⋅ E
Упругое       деформирование материала	2 т W < τn 2 ⋅ E

Здесь: E – модуль упругости, Па; τ – предел Пайерлса, Па; σ – предел прочности на растяжение, Па.

Сравнение величины минимальной и максимальной допустимых энергий воздействия показывает, что величина энергии воздействия, соответствующая началу пластических деформаций в твердых минералах, более чем на 5 порядков меньше, чем энергия воздействие хрупкого разрушения. Широкий интервал энергетического диапазона квазипластичного разрушения поверхностного слоя твердых минералов затрудняет задачу выбора оптимального режима механического воздействия.

Для моделирования поверхности нанометрового микрорельефа рассмотрено послойное квазипластическое удаление поверхностного слоя под действием усталостных напряжений возвратно-поворотных мод деформации. Задача решается в плоском приближении.

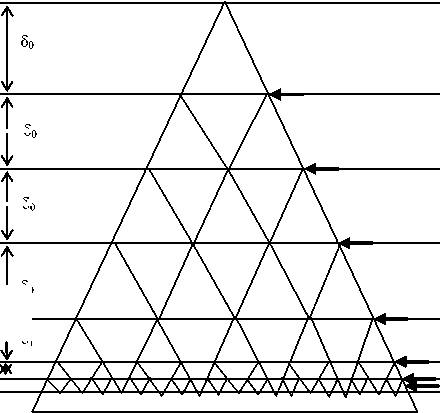
Пусть δ - подача шлифовального круга по вертикали, м. Если δ < h , где h –высота выступа образца (шероховатость R ), м, то столкновения выступов ОП образца с зернами шлифовального круга будут происходить в слое толщиной δ (рис 2).

На начальном этапе размер алмазных зерен шлифовального круга соизмерим с размером микронеровностей обрабатываемого материала (20 мкм). На заключительных этапах шлифования размер зерен ШК значительно превышает оставшиеся микронеровности, составляющие 2-10 нм. Примем средний диаметр части выступов механизма взаимодействия алмазных зерен шлифовального круга с обрабатываемой поверхностью и части зерен шлифовального круга, попавших в этот слой, d ∼ δ/2. Согласно предложенной модели при выбранном шаге подачи 5, м, за цикл снимается слой 50, но нижняя часть (впадины) шероховатости перемещаются на 2 50, до тех пор, пока подача не станет порядка высоты выступов (шероховатости R ).

8 з

8 о

8 о

Рис. 2 Схема удаления ПС образца при квазипластичной обработке

б о

На это необходимо k

циклов,

^к1 =

h ₀

- ¹,

где

h ₀

целая часть

выражения. С этого момента усилие прижима инструмента (вертикальная врезная подача инструмента) должно уменьшаться. При уменьшении подачи по закону 5 =

₂ k 2

уменьшение усилия прижима будет продолжаться до тех

пор, пока подача инструмента не сравняется с технически достижимой подачей шлифовального круга по вертикали 5 ^_п. Общее число шагов, исчерпывающих технические возможности шлифовального станка, равно:

5/ h0

ln 0

к =

5 min

.

ln2

Исходя из заданной шероховатости и минимально возможной врезной подачи станка можно вычислить число снимаемых слоев, время, необходимое на доведения заготовки до заданной шероховатости, и выбрать рациональный режим обработки.

Оценка минимального размера шероховатости, возможного получить на используемом оборудовании, исходит из технически достижимой подачи ШК по вертикали 8min. Высота получаемого выступа шероховатости hB - 5 min /2 +5тепл/2. Дальнейшего снижения шероховатости при квазипластичном удалении ПС можно добиться при нулевой подаче инструмента, создавая усилия прижима за счет теплового расширения образца. Оценочное значение минимальной шероховатости Rz: hmin - 3,^ /2,; ЗтепЛ = в • H • АТ;^, где β – средний коэффициент линейного расширения материала образца, К-1; H - толщина образца, м; ∆T –разница между интегральной средней температурой обрабатываемой поверхности , К, и температурой окружающей среды, К.

Влияние теплового фактора является наиболее существенным при удалении поверхностного слоя минерала в режиме квазипластичности. Его рост при жестком закреплении образца будет приводить к необходимости снижения начального усилия прижима, что обусловлено тепловым расширением образца и увеличением подвижности дефектов в энергетической области квазипластичности [4].

–

Схематично система «инструмент представлена на рис. 3.

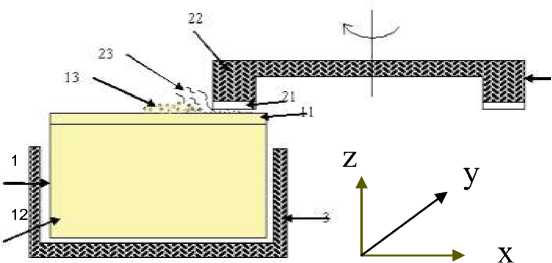
обрабатываемый материал»

1-образец; 11-поверхностный слой образца; 12-внутренний объём образца; 13-пыль от обработки образца; 2-шлифовальный круг; 21-поверхностный слой шлифовального круга; 22-внутренний объём шлифовального круга; 23-пыль от шлифовального круга; 3-державка

Рис.3. Система «инструмент-обрабатываемый

Введенная энергия в системе «инструмент- обрабатываемый материал» расходуется на работу силы трения. В процессе обработки образца происходит периодический нагрев в зоне обработки и пассивное воздушное охлаждение образца при выходе из зоны обработки. При увеличении поступления теплового потока в результате работы силы трения A происходит нагрев образца и распространение теплового потока вдоль оси Z образца. Под действием теплового потока q с той же периодичностью вследствие теплового расширения возрастает усилие прижима кристалла к ШК. Чтобы не допустить скола минерала, необходимо рассчитать предельно допустимое усилие прижима и установить зависимость его изменения в процессе обработки от величины поступающего теплового потока. Для расчетов необходимо знать зависимость коэффициента теплового линейного расширения от температуры и для каждого обрабатываемого минерала определять критическую температуру, при которой тепловой поток в образце достигнет критического значения.

Точный аналитический расчет распределения температуры в образце, необходимый для расчета масштабов его теплового расширения, затруднен, вследствие неточности в определении тепловых параметров на границах образца в процессе обработки. Технически проще измерять температуры «горячей» и «холодной» поверхностей, а не тепловые потоки. В качестве первого приближения распределение температуры можно определить, решая известное дифференциальное уравнение теплопроводности для неограниченной пластины с периодическими граничными условиями первого рода. Сделав замену переменных и рассматривая изменения температуры поверхности в безразмерных координатах (рис.4), получим уравнение и граничные условия в безразмерном виде:

дО д 2О дFo

При £ = 0 О = 1 при 0 <   Fo < Fo 1 ; О = 0 при Fo 1 <   Fo < Fo₀ .

При £ = 1 0 = 0 Fo = aT, Fo0 = at^, Fo, = at^, Fo. = a(t0 - t1}, 9 = TT

2 ’     0       2 ’     1      2 ’     2           2             TT где Fo -текущее значение критерия Фурье; а - температуропроводность; т -текущее время; h -толщина образца; t1- длительность периода нагрева; t0 -длительность периода охлаждения; (t0 - t1) - время от начала одного цикла нагрева до начала другого периода нагрева; Fо1, Fо0 - соответствующие значения критерия Фурье; ^-безразмерная координата; 0-безразмерная температура; х -текущая координата; Т0 - начальная температура среды; Т1 -температура поверхности нагрева при x=h.

Период обработки

Период охлаждения

Рис.4. Схема изменения безразмерной температуры поверхности образца при обработке материала

Применяя описанное Карслоу Г., Егер Д. квазистационарное асимптотическое решение данного уравнения при n ^ ^ , получим :

В период обработки ( 01)

В период охлаждения ( t_x <  т <  t ₀), т * = т - t_x , 0 <  т *< t₀ - t_x .

Исходные данные: - для лейкосапфира:

α =8^.10^-7 м²/с, h = 0,02 м, τ = 0,5 с, t =5 c, F =10², F =10^-3,      F =0,9

1                    000                            0

. ₁₀-2_;

• - для алмаза : α =4,85^.10^-4 м²/с, h = 0,002 м, τ =0,5 с, t =5c, F =550,

1                    0                02

F 0 =60, F 0 =600 .

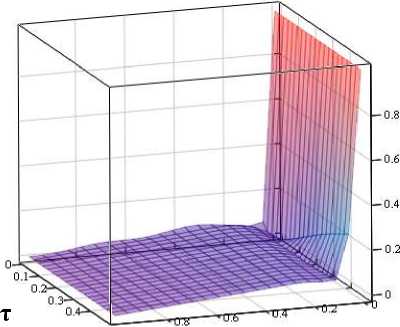
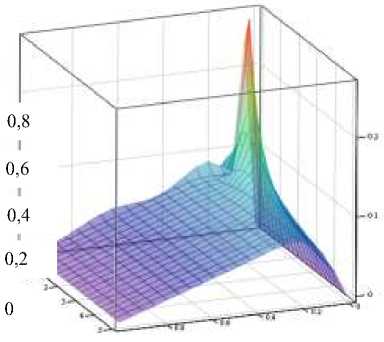
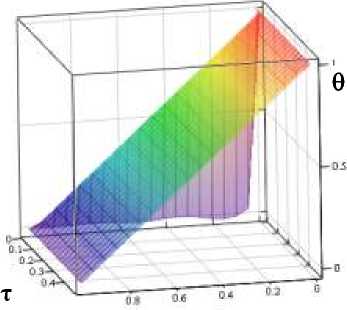
Графическое изображение температурных процессов при квазипластичном удалении поверхностного слоя минералов приведено на рис. 5, 6.

ξ

θ

ξ

В период обработки лейкосапфира

ξ

В период обработки алмаза

В период охлаждения лейкосапфира

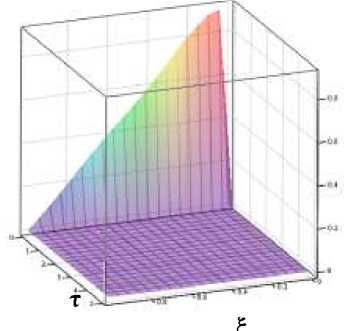
θ

В период охлаждения алмаза

Рис.5. Зависимость безразмерных температуры и координаты образца от времени

θ

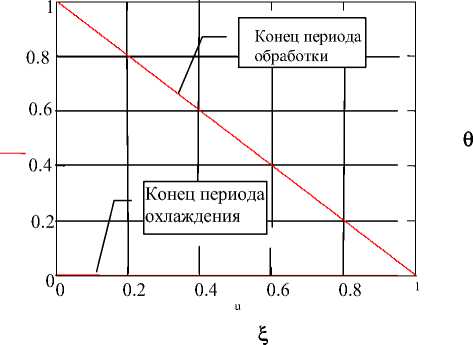
Рис. 6.Зависимость безразмерной температуры образца от координаты.

Средняя безразмерная температура в конце периода нагрева алмаза 0,5

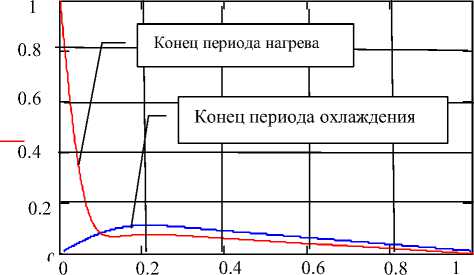
ξ

Средняя безразмерная температура в конце периода охлаждения алмаза 0,0

Средняя безразмерная температура в конце периода обработки лейкосапфира 0,077

Средняя безразмерная температура в конце периода охлаждения лейкосапфира 0,042

При рассмотрении тепловых процессов, сопровождающих обработку в режиме квазипластичности, разработаны критериальные зависимости, определяющие условия, при которых процесс обработки не будет переходить из области квазипластичности в область хрупкого разрушения.

Критерий хрупкого термического разрушения характеризует устойчивость минерала к хрупкому термическому разрушению.

Возникающие в процессе обработки минерала термические напряжения σТ под действием нормальной составляющей силы прижима, определяемой врезной подачей, не должны превосходить предел прочности минерала сжатие. При разработке критерия хрупкого термического разрушения была взята за основу формула, описанная Гончаровым С.А. Дополнительно учитывлась зависимость коэффициента теплового расширения материала от температуры, получаем:

П т

E * в о

-------7 ----------Г *

² " ( 1 ^{- ц}

A T +

к *А T²

< ^П сж , сж

где в - коэффициент линейного теплового расширения материала образца, К^-1; ц - коэффициент Пуассона, E - модуль Юнга, Па, A T = T - T_o , T

• - температура образца, К, Т_о - температура среды, К, в — коэффициент линейного теплового расширения при 20˚С.

В первом приближении в = в ( 1 + k A T ) .

Критерий хрупкого термического разрушения монокристаллов для процесса поверхностной обработке в режиме квазипластичности:

к =    E * во хттр   2 .(1 - ц)* Псж

* A T + к *АА

< 1 .

Для поликристаллов термическое разрушение происходит прежде всего за счет разницы между коэффициентами теплового расширения соседних микрокристаллов Р 1 и p₂.

Критерий хрупкого термического разрушения поликристаллов для процесса поверхностной обработке в режиме квазипластичности:

k xтрм

E • E 2 ■ ( P 2 - P i ) A T +

в 2 ■ k 2 - Py k 1 ,_ДГ2 2

( E + E 2 Ут д.

< 1,

где E и E , k и k – модули Юнга и коэффициенты температурной зависимости коэффициента линейного теплового расширения соседних микрокристаллов.

Следующим критерием, характеризующим тепловое воздействие на обрабатываемый минерал при поверхностной обработке в режиме квазипластичности, является критерий сохранения формы k (рис. 7) .

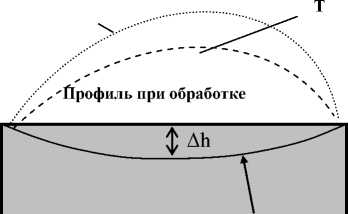
Профиль при остывании

Рис. 7. Форма обрабатываемого минерала при обработке

В процессе обработки распределение тепла по обрабатываемому минералу происходит неравномерно. Благодаря внешнему охлаждению при обработке основному нагреву подвергается центральная часть поверхностного слоя, непосредственно находящаяся в зоне обработки. Усилие прижима F и величина съема будут максимальными в центре образца. Толщина центральной части образца при охлаждении до исходной температуры уменьшается на величину A h , м: A h = A T ■ P ■ h , A h <  5, где 5 -величина подачи инструмента, м; h - начальная толщина образца, м; A T_cp -разница между средней интегральной температурой образца в процессе обработки и температурой окружающей среды, К.

Основное условие получения обрабатываемой поверхностьи заданной неплоскостности имет вид:

,     A Тср • P • hо k =-----------® 1.

ф       5

При соответственном подборе режимов обработки, руководствуясь приведенными выше критериями хрупкого термического разрушения, можно обрабатывать минерал так, чтобы устранить негативное влияние теплового расширения минерала при поверхностной обработке.

Режим квазипластичной поверхностной обработки     хрупких материалов можно обеспечить при специальном подборе таких параметров, как усилие прижима и скорости движения инструмента параллельно поверхности кристалла, подвергаемой механическому воздействию. Поскольку в обрабатываемом материале возникают термоупругие напряжения, которые способствуют распространению дефектов, и возможному разрушению материала, необходимо на начальном этапе обработки задать режимы, при которых не произойдет разрушения образца. Эмпирический поиск рациональных режимов, как правило, сопровождается большими затратами времени и опытных образцов дорогостоящих материалов. Зная распределения температуры образца при обработке и зависимость теплового расширения материала обрабатываемого образца от температуры можно определить интегральное тепловое расширение образца, сопоставить его с деформацией упругой обрабатывающей системы и регулировать усилие прижима таким образом, чтобы предотвратить скол образца. При рассмотрении критерия хрупкого термического разрушения для выбора рациональных режимов квазипластичной обработки можно выделить ряд факторов, присущих обрабатываемому минералу, имеющих табличное значение, которые могут определяться до процесса обработки.

При обозначении из формулы (1)

условие получения бездефектной обработке можно представить в виде:

АΔТ +ВΔТ = σ_{процесса} ≤ τ_с д   , где

E • во _      E • во • к

2(1 - д)" A;  4(1 - д)" B поверхности при квазипластичной

τ сд – предел прочности на сдвиг, Па

Критерий хрупкого термического разрушения для монокристаллов:

А •A T + B •A T² _<

^Т сд

Для разных материалов составлен классификатор температурных областей применения режимов обработки, при которых не будет происходить разрушение материалов. В табл. 3 приведены значения постоянных факторов для лейкосапфира, алмаза и кварца. Подобным образом рассчитаны значения коэффициентов для других материалов.

Таблица 3.

Материал	А, К-1	В, К-2
Лейкосапфир	2124,77·103	1062,385·k·103
|| c-оси
± с-оси	1470,345·103	735,1724·k·103
Алмаз	3683,532·106	1841,766·k·106
Кварц	822,7714·103	411,3857·k·103

Аналогичные преобразования делаются для критерия термического хрупкого разрушения поликристаллических минералов (2):

E 1 ⋅ E 2 ⋅ ( β 2 - β 1 ) ⋅∆ T E 1 ⋅ E 2 ⋅ ( β 2 ⋅ k 2 - β 1 ⋅ k 1 ) ⋅∆ T ² = A ; = B .

E + E E + E

Из приведенных выражений можно определить допустимые области изменения температуры при обработке в режиме квазипластичности для различных минералов.

Объективность научно обоснованных рекомендаций, разработанных в данной главе, подтверждена результатами опытно-промышленной апробации. Аналитические исследования образцов до и после экспериментов проводились на оптическом интерферометре белого света Zygo (New Vew 5000) в ЦЕНИ ИОФ им. A.M. Прохорова РАН, разрешение в плоскости объекта 0,45 мкм по оси Y - 1 A. Наилучшие результаты шероховатости 2,5 нм на участке поверхности поликристаллического алмаза и 1,95 нм на участке поверхности лейкосапфира получены в процессе обработки шлифовальными кругами с разной крупностью зерна на финишной обработке при определенных режимах процесса квазипластичной обработки.

Процесс квазипластичной обработки носит автоколебательный характер и прослеживается из анализа осциллограмм.

Акустический сигнал, генерируемый в процессе квазипластичной обработки поверхности минералов, может использоваться не только для контроля качества обрабатываемой поверхности, но и для управления процессом обработки. Методом осциллографического контроля можно воспользоваться для автоматизации поверхностной обработки твердых хрупких материалов с получением нанометрового рельефа поверхности со стабильно воспроизводимыми результатами [6].

При квазипластичной обработке формирование нанометрового рельефа поверхности возможно при различной крупности зерна шлифовального круга, так как доля хрупкого разрушения при правильно подобранных режимах обработки минимальна.

Фотографии обработанных поверхностей алмаза и лейкосапфира приведены на рис.10 .

Способ обработки твердых минералов в режиме квазипластичности является перспективным для автоматизации процесса обработки, поскольку имеет возможности осуществления технологической диагностики различными аппаратными средствами, дополнительного контроля качества обрабатываемых изделий и групповой обработки изделий из твердых минералов.

а

б

д

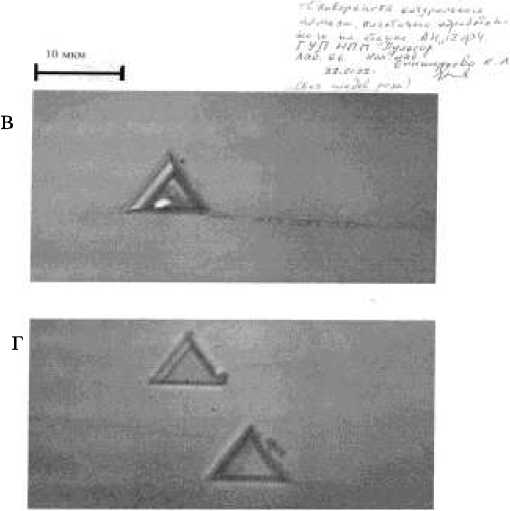
Рис. 10. Обработанные поверхности алмаза и лейкосапфира. а – натуральный алмаз (обработанная и необработанная поверхности); б – монокристалл лейкосапфира (диаметр 31 мм);

в, г – натуральный алмаз (показаны прошлифованные включения алмаза в алмазе в «твердом» направлении);

д – отшлифованная подложка ИМС из лейкосапфира.

Выводы

Квазипластичное удаление поверхностного слоя твердых хрупких материалов актуальна для получения поверхностей материалов электронной техники с нанометровым рельефом поверхности без дефектов, привнесенных процессом обработки. При автоматизации процесса обработки возможно серийное производство изделий для микроэлектроники со стабильно повторяющимися      выходными      параметрами.      Применение осциллографического контроля в процессе обработки позволяет увеличить выход годной продукции и выявлять дефектные изделия на этапе шлифования. Получение нанометровой шероховатости поверхности (210 нм) на этапе алмазного шлифования позволяет сократить время полирования, а иногда позволяет отказаться от этапа полирования.

Solid brittle materials and minerals (such as diamond, leikosapphire) are adapted in microelectronics for preparing the base layers. Quasi-plastic grinding makes it possible to simulate the surface of high quality with the roughness of 1-10[nm] without the polishing. The acoustic fluctuations, generated by billet in the working process, can be used for the control of working process, and also can be used for control of quality of the finished surface of the materials.