Лавинное умножение и излучательная рекомбинация носителей тока в кремниевых солнечных элементах

Солнечные элементы широко используются в качестве источников энергии, в том числе на энергетических платформах космических аппаратов. В обратно смещенных p–n-переходах, расположенных у поверхности полупроводника (как, например, в светодиодах и солнечных элементах), в предпробойных электрических полях наблюдаются светящиеся точки и пятна, названные в [1] микроплазмами. Микроплазменный пробой, происходящий в обратно смещенных p–n-переходах, сильно локализован, не превышает 1 мкм в диаметре и сопровождается свечением невысокой интенсивности [2]. Интенсивность этого свечения и количество микро- p–n-переход.

плазм возрастают при увеличении прикладываемого к p–n- переходу напряжения.

Локализация микроплазм может быть вызвана резким возрастанием электрического поля в области свечения и увеличением коэффициентов лавинного умножения. Вероятнее всего это происходит в местах, где имеются неоднородности p–n-перехода. Такие неоднородности могут быть связаны с микродефектами, флуктуациями фронта легирования, дислокациями и др. В этих локальных областях может происходить уплотнение электрического поля E > Eп, где Eп – пороговое поле для лавинного умножения носителей тока. Предполагается, что свечение микроплазм является результатом рекомбинации «горячих» электронов и дырок, ускоренных в таких сильных полях (E > Eп) до ударно-ионизационных энергий.

Оценка качества полупроводниковых пластин и солнечных элементов, основанная на применении микроплазм, представляет большой интерес для обнаружения микродефектов, тип которых можно определить, используя электронно-микроскопические методы.

Экспериментальная часть. Объектом исследований являлись солнечные элементы, изготовленные на основе монокристаллического кремния, в которых p- слой был изготовлен путем легирования бора с концентрацией до 10 ¹⁶ атомов/см³, а n- слой – диффузионным способом с применением легирующей примеси атомов фосфора с концентрацией до 10²¹ атомов/см³. Расположение p–n -перехода на глубине 0,4 мкм от лицевой поверхности солнечных элементов позволяло наблюдать в оптическом микроскопе микроплазменное свечение, возникающее в обратно смещенном p–n -переходе. Электронно-микроскопические исследования дефектов в области p–n- пере-ходов солнечных элементов осуществлялись с помощью просвечивающего электронного микроскопа JEM-2100.

Причины возникновения микроплазм. Причиной возникновения микроплазм могут служить неоднородности p–n-переходов, связанные со структурными дефектами в этой области полупроводника, например с дислокациями. Во-первых, в районе дислокации имеются области сжатия и растяжения кристаллической решетки. В области сжатия (растяжения) вблизи дислокаций ширина запрещенной зоны может уменьшиться на 0,2…0,4 эВ. Так как пороговая энергия ионизации принимается пропорциональной ширине запрещенной зоны, то ее уменьшение вблизи дислокаций должно привести к увеличению коэффициентов ионизации носителей и, следовательно, к микроплазменному пробою. Во-вторых, дислокации в кристаллах являются центрами осаждения примесей, которые могут формировать примесные атмосферы вокруг дислокаций или в результате распада пересыщенного твердого раствора – выделения второй фазы. Наличие примесных атмосфер легирующих примесей должно приводить к локальному изменению области про- странственного заряда и к увеличению напряженности поля в местах пересечения p–n-перехода дислокацией. Выделения второй фазы могут являться одной из главных причин, способствующих понижению напряжения пробоя p–n-перехода. В-третьих, вдоль дислокаций могут быть повышены коэффициенты диффузии примесей, что также может привести к резкому понижению напряжения пробоя.

Типичные фотоснимки микроплазм на поверхности солнечных элементов при возрастающих обратных напряжениях представлены ниже (рис. 1).

Существует большое количество фактов, подтверждающих, что включения второй фазы являются одной из основных причин ухудшения обратных характеристик полупроводниковых p–n- переходов [3]. Выделения второй фазы встречаются практически во всех полупроводниковых материалах. Форма включений может быть самой разнообразной: сферической, цилиндрической, дискообразной или иглообразной [3]. Локальному понижению напряжения пробоя также может способствовать искривление фронта диффузии, например при диффузии легирующей примеси вдоль скопления дислокаций.

Типичными дефектами в кремнии являются краевые и винтовые дислокации, которые могут быть декорированы примесными преципитатами, образовавшимися в результате диффузии примесей из объема полупроводника на дислокации с последующим распадом пересыщенного твердого раствора [3] (рис. 2).

Ниже будет приведено описание генерационно-рекомбинационных процессов с оценкой кинетических параметров и условий излучательной рекомбинации носителей тока в микроплазмах.

О разогреве носителей тока в сильном электрическом поле. Микроплазмы возникают при увеличении обратного напряжения, приложенного к p–n- переходу, когда напряженность электрического поля в области пространственного заряда достигает значений, при которых наблюдается ударная ионизация. В общем случае в ударной ионизации могут принимать участие носители, как инжектированные в область пространственного заряда, так и генерированные в этой области.

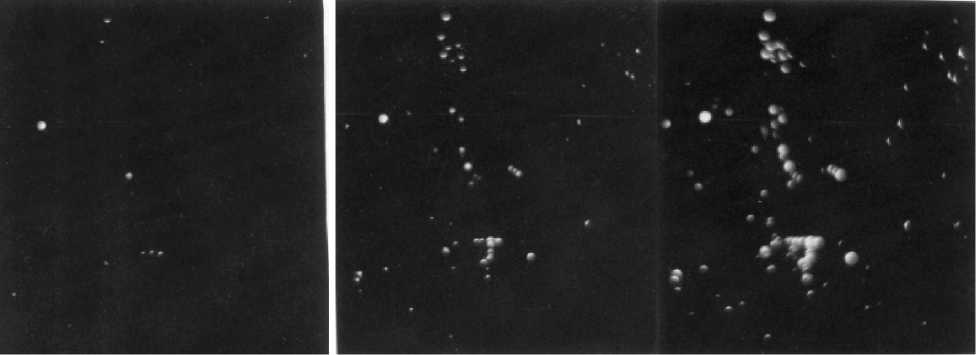
а

б

в

Рис. 1. Увеличение интенсивности и числа микроплазм в кремниевом солнечном элементе при повышении напряжения: а – 7 В; б – 8 В; в – 10 В

Под разогревом принято понимать увеличение средней кинетической энергии броуновского движения частиц (электронов или дырок) в электрическом поле сверх их среднерешеточной тепловой энергии. Запишем уравнение разогрева в обычной форме:

dp.              z dS = qE - S (e, E), dx

где q и e - заряд и энергия частицы; Е - напряженность электрического поля; S ( e , E ) - уменьшение потери энергии, испытываемое частицей на единице пути по направлению ее дрейфа.

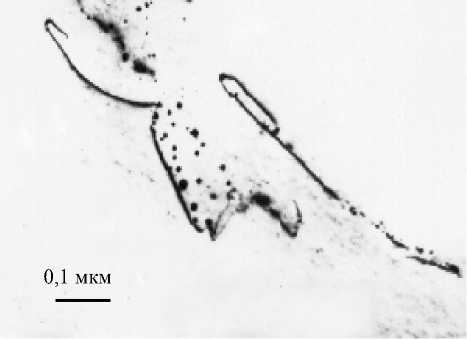
Рис. 2. Электронно-микроскопическое изображение примесных выделений на дислокациях в кремнии в области p–n- перехода

Проведем окончательные расчеты зависимости S ( e , E) от энергии частицы ( e ) при ее торможении в столкновениях с акустическими колебаниями решетки. Для этого воспользуемся приведенными в [4] выражениями, согласно которым S ( e , E ) можно приве сти к виду

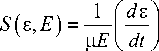
где

de_ 2 qUe(М/2 <1 - 2kT) dt А,      Ц0 v kT J I e J,

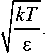
Здесь µ0 – подвижность частиц при температуре решетки Т, Ue – скорость акустических волн в кристалле; k – постоянная Больцмана. При этом уравнение (1) перепишется в виде d e г — _ qE dx

1 - 2 1 ^U e | I ^e | | 1 - ^{2 kT} | (ц E J V kT J ( e ^J

В протяженном однородном электрическом поле электроны ускоряются до предельной энергии, определяемой

d s из условия — _ dt

Из равенства нулю квадратной скобки уравнения (5) находим eнас _ kT(1 + VTTO2),               (6)

где

1 OoE a _ —;= ——. 2 Ue (7) В безразмерных переменных e          s      1 У _ —, y _ -нас-, — = kT нн  kT  A qE V1 + a2 kT a2 (8) интегрирование уравнения (1) при начальных условиях x = 0, y = 1 может быть представлено в виде

I X |

У = 1 + (Ут -1) th Ы.(9)

VA|

В сильных полях (a >>1) из (6) и (8) имеем eHac _ kTa,(10)

kT kT ц

A _ a _      0;=.(11)

qE    qU_e 2

В предпробойных электрических полях часть электронов может достигать энергии e >  e . , достаточной для ударной ионизации. Полагая, что е _нас = e i , из (9), (10) и (11) найдем выражение для напряженности поля E_i – стартового для лавинного умножения носителей тока:

s х.

E _-^ cth - i -, ‘ q A    A

где x_i – протяженность участка сильного поля ( E >  E_i ).

Полагая для кремния e i = 3,6 эВ, U e = 5^10 5 см/с, ц₀= 10³ см/(В•с), из формул (10).. .(12) получим A = 3• 10^-5см, E_i = 1,4 ∙10⁵ В/см.

Подобные расчеты были проведены и для случая, когда хаотизация и торможение движения носителей тока осуществлялись оптическими и пьезоэлектрическими фононами. В приближении e >>  kT D , где T D - температура Дебая, для рассеяния на оптическом деформационном потенциале получены следующие выражения для A , e и E i :

I - ^- 1

e_e н _ac | 1 - e ^Al ,                     (13)

S hoc _ qE A , A_ bqE ,              (14)

где b _ 2 kT D

। nph ² | 2 m ² DN„ I

.

Полагая для оценок D ® 8^10 8 эВ/см, N ® 0,1, p = 2,3 г/см 3 , найдем E i = 10⁵ В/см, A = 3,6^10^-5см.

В пределах допусков при выборе параметров, входящих в формулы (10)…(12) и (13), можно считать, что в кремнии роль акустических и оптических фононов в про- цессах торможения и хаотизации горячих носителей тока примерно одинакова. Полученные значения A, Ei и-i со- поставлены с соответствующими значениями, характе- ризующими лавинное умножение в p–n-переходах.

Обоснование эстафетной модели лавинного умножения в p–n-переходах. Для оценок напряженности электрического поля Е и его протяженности l в обратно сме- щенном резком p–n-переходе воспользуемся следующими приближенными формулами [5]:

1 2 ee ₀ V qN

E_ml _ 2 V ,

где V – приложенное напряжение; N – эффективная концентрация основных легирующих примесей (акцепторов и доноров); ee ₀ - диэлектрическая проницаемость полупроводника; E_m – напряженность поля в середине p – n -перехода.

В этом приближении протяженности x_i участка сильного поля ( E_i <  E <  E_m ) может быть определена из уравнения

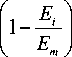
в котором E_i зависит от x_i по формуле (12).

Для типичного p-n-перехода, у которого N ® 1017 см-3, первые признаки лавинного умножения проявляются при обратных напряжений V ® 10 В. При этом с помощью выражений (15) и (16) находим l® 4^ 10-5 см, Em ® 3^105 В/см и xi = 3∙10–5 см.

Учет неоднородного распределения примесей в p – n -переходах не существенно уточняет эти оценки. По порядку величины х. и X , определяемые выражением (14), одинаковы, что противоречит классической модели лавинного умножения [1], которая справедлива при х . >> X (условие непрерывности ионизации). Это означает, что на самом деле лавинное умножение на однопролетных участках сильного поля ( х . ® X ) осуществляется по эстафетной модели [6]: электроны в конце участка (0 <  x <  x_i ) генерируют дырки, которые, ускоряясь в обратном направлении, в начале этого участка генерируют электроны, и количество таких циклов взаимной генерации носителей тока может быть достаточно большим:

V = vd- » 10¹² c ^{- 1}, x_i

где v_d – предельная (~ 10⁷ см/с) скорость зарядов в сильном поле.

Формально этот процесс описывается уравнениями [6]:

К = jn 0 + Y pjp, jp = jp0 + Y nj,                  (18)

где j n ₀ и j p ₀ – стартовые; j_n и j_p – полные потоки электронов и дырок в p - n -переходе; у _n и у p - коэффициенты ударной ионизации частиц после их ускорения на лавинном участке.

Таким образом, анализ интенсивности и количества микроплазм, возникающих на лицевой поверхности солнечных элементов при увеличении приложенного к p–n -переходу обратного напряжения, может являться экспресс-методом обнаружения микродефектов и оценки качества солнечных батарей.