Лазерные пучки Айнса–Гаусса как суперпозиция пучков Эрмита–Гаусса или Лагерра–Гаусса

Для управления светом деталями микромашин и создания множественных оптических ловушек для микрочастиц удобно использовать лазерные модовые пучки, которые сохраняют свою структуру, в том числе в фокусе сферической линзы, и симметрию которых можно менять, изменяя некоторый параметр и переходя от декартовой симметрии через эллиптическую к круговой симметрии. В качестве таких лазерных пучков можно использовать модовые пучки Айнса–Гаусса (АГ), которые при изменении параметра эллиптичности преобразуются либо в пучки Эрмита–Гаусса (ЭГ), либо в пучки Лагерра–Гаусса (ЛГ).

Решение уравнения Уиттекера в виде функций АГ было впервые получено Арскоттом в [1, 2]. В книге Миллера [3] это решение в разделяющихся переменных получено в эллиптических координатах. В оптике пучки АГ были рассмотрены в [4]. В [5] приведены простейшие пучки АГ, когда зависимость от параметра эллиптичности отсутствует. В [6] рассмотрены элегантные пучки АГ. После этих работ пучки АГ нашли широкое применение в оптике, наряду с другими известными модовыми пучками (ЛГ и ЭГ). Так, в [7] пучки АГ были созданы с помощью цифровой голограммы. В [8] были сформированы векторные (классически перепутанные) пучки АГ, а именно, формировалась суперпозиция, в которой четный пучок АГ имел правую круговую поляризацию, а нечетный пучок АГ имел левую круговую поляризацию. Пучки АГ с квантовой перепутанностью были сформированы в [9]. Также нелинейное преобразование пучков АГ с помощью спонтанной параметрической конверсии рассматривалось в [10, 11]. В [12] также были параметрически сформированы пучки АГ, но без конверсии. В [13] элегантные пучки АГ рассмотрены в параболической среде. Распространение пучков АГ в одноосных кристаллах исследовалось в [14]. Пучки АГ используются для передачи информации под водой [15]. Распространение пучков АГ в турбулентной атмосфере рассматривалось в [16].

Из приведенного обзора работ по пучкам АГ видно, что они интенсивно исследуются в оптике, но аналитическое представление этих пучков через моды ЛГ и ЭГ с явной зависимостью от параметра эллиптичности в рассмотренных работах отсутствует. Чтобы преодолеть этот недостаток, в данной работе приведены аналитические формулы разложения четных и нечетных мод АГ с индексом p =3, 4, 5, 6 по модам ЛГ и ЭГ. Явная зависимость коэффициентов разло- жения от параметра эллиптичности ε позволяет управлять формой распределения интенсивности пучков АГ, непрерывно изменяя этот параметр. Заметим, что в данной работе впервые в оптике параметр эллиптичности ε рассматривается не только положительным, но и отрицательным. Показано, как изменяется пучок АГ при изменении знака этого параметра. Представление каждой моды АГ в виде двух разложений (по базису мод ЛГ и по базису мод ЭГ) позволяет сделать очевидным вывод, что при стремлении параметра эллиптичности ε к нулю любая мода АГ сводится к некоторой моде ЛГ (точнее, её вещественной или мнимой части), а при стремлении параметра ε к бесконечности мода АГ совпадает с некоторой модой ЭГ.

1.    Решение параксиального уравнения в эллиптических координатах

Параксиальное уравнение Гельмгольца имеет вид [3]:

I '.■'.■ 2 ik —I E ( r , z ) = 0,                        (1)

где     (x, y, z)     – декартовы координаты, r = (x, y) = (r cos ф, r sin ф) - двумерный вектор, координата z направлена вдоль оптической оси, k – волновое число света, E (r, z) – комплексная амплитуда монохроматического светового поля. Перейдем к безразмерным единицам: x:=x /w0, y:=y /wо, z := 2z/(kw2), где w0 – радиус перетяжки Гауссова пучка. Тогда уравнение (1) в безразмерных переменных примет вид:

I ' 4 i —I E ( r , z ) = 0.                        (2)

Простейшее его решение, обладающее конечной энергией, – это стандартный Гауссов пучок:

поперечного распределения интенсивности таких полей с точностью до масштаба совпадает с интенсивностью поля на начальной плоскости z =0:

H n , m ( r , z ) =

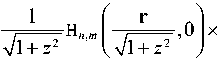
I izr2, x exp--1 (n + m + 1)arctg z ,

11 + z2)

L n , ± m ( r , z ) =

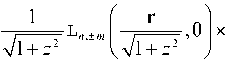
I izr2

x exp-- 1 (2 n + m + 1)arctg z .

1 I 1 + z2     'J

Поэтому достаточно исследовать оба семейства при z =0, опуская последний аргумент для краткости: H n , m ( r , 0) = H n , m ( r ) И C n , ± m ( r , 0) = C n , ± m ( r ) -

Введём также нормированные версии каждого семейства решений:

HG n , m ( r ) =

LG n , ± m ( r ) =

Ц. I^ nm (ri = ^

^C ± ^r, |C,₄ .(rm =©E m II C n ,± m (r)||  ¹¹ -^UM2   2 ^m n !

Если при решении уравнения (2) устроить разделение переменных в эллиптических координатах ( ^ , n ) [3], то получится семейство пучков АГ, которые также являются структурно устойчивыми:

p /2

I ( r , z ) = G ( r , z )I-^- I P©Q ( n ).             (7)

1 1 + iz )

Здесь

—. x    = ch С cos n ,   —, y    = sh С sin n ,     (8)

a V1 + z ²                ay 1 + z ²

и параметр a пока произволен. Подставляя выражение (7) в уравнение (2), получим уравнения на функции P (© и Q ( n ):

Известно, что разделение переменных при решении уравнения (2) в декартовых и полярных координатах позволяет получить два семейства решений – соответственно пучки ЭГ и ЛГ [17]:

^ - 2a2sh2^ - (X - 2pa2ch2C) IP© = 0, de2            oc)

,                         \(9)

d2                  дI

--+ 2 a ² sin2n-- + ( X - 2 p a ² cos2 n ) | Q ( n ) = 0.

5n2          ©

Hn, m (r, z) = G (r, z) x n+m        ,        __ ,         ,        __

1 - iz 1 ² H I x IW I у

1 + iz ) n I 1+^ J m I 1

m

. .             ( 1 - iz i nn ⁺ 2 . I 2 r ² 1

L n , ± m ( r , z ) = G ( r , z ) -—-      L m  ----- r m e ± ^{im ф} ,

11 + iz J 11 + z2 J где n, m =0, 1, 2....

Оба семейства являются примерами структурно устойчивых световых полей, т.е. при любом z форма

Оба уравнения (9) сводятся к уравнению Айнса, канонический вид которого следующий [1 –3]:

52              d

—- + esin21 — + (X-p£cos21) |N(t) = 0,(10)

312           31)

где p - целое неотрицательное число, £ - положительный параметр и X = X (p, £) - некоторая константа. Для уравнения (9) это константа, которая возникает при разделении переменных С и n в уравнении (2). Для уравнения (10) это вещественное число, смысл которого состоит в том, чтобы обеспечить существование решения N (t) в виде тригонометрического многочлена p-й степени (его называют многочленом Айнса). При наложении такого ограничения на вид решения оказывается, что X должно быть корнем некоторого многочлена (р + 1)-й степени с коэффициентами, зависящими от £ (корнем характеристического уравнения). Всего, таким образом, появляется (р +1) корней: X0, Xi,..., Xр, причём все они вещественны. Более того, если эти корни расположить по возрастанию при £ = 0, то с ростом £ они не перепутываются - порядок по возрастанию остаётся неизменным (при всех положительных £ характеристическое уравнение не имеет кратных корней). Тем самым, выбрав корень Xq (р, £) и построив тригонометрический многочлен Айнса N(t)= Np,q (t, £), решение (7) можно записать через решения уравнения (10) в виде:

I p,q ( r , z ) = G ( r , z )

л p ^/2 I 1 — iz I 1 1 + iz J

N p , q ( i ^ , £ ) N p,q ( П , £ ),(11)

где £ = 2 a ². Можно показать, что характеристическое уравнение факторизуется и распадается на два уравнения. Если p чётно, то имеется p /2 нечётных многочленов Айнса (они записываются через синусы кратных углов, и их обычно нумеруют индексом q = 2,4,..., p ) и p /2 + 1 чётных многочленов Айнса (они записываются через косинусы кратных углов, и их нумерация q = 0, 2, 4,..., p ). Если p нечётно, то имеется поровну (p + 1)/2 чётных и нечётных многочленов Айнса (здесь нумерация q = 1, 3,..., p ). Поэтому чётные и нечётные моды АГ (11) обычно записывают в следующем виде:

^{p /2}

IG p , q ( r , z ) = G ( r , z ) I        I c p ^q\i ^ , £ ) C pq ) ( n , £ ),

V 1 + iz j pi-iAp/2 , ,

IG p , q ( r , z ) = G ( r , z ) I        I S pq ) ( i ^ , £ ) S pq ) ( n , £ ),

V 1 + iz J

где C pq ) ( t , £ ) и S p^q ) ( t , £ ) - чётные и нечётные многочлены Айнса, соответственно, индексы p и q - неотрицательные целые числа, причём q <  p .

К сожалению, традиция записывать чётные и нечётные моды АГ по-разному и рассматривать по отдельности приводит к неоправданным усложнениям в обозначениях: индекс q выбирается той же чётности, что и p , т.е. q = { p , p -2, p -4,...}. Если p нечётно, то этот перечень останавливается, дойдя до q = 1, а если p чётно, то дойдя до q = 0 для IG e -мод и до q = 2 для IG o -мод. Это разделение, по-видимому, связано с исходной записью многочленов Айнса N ( t ) через sin kt или cos kt . Если вместо синусов и косинусов использовать e^ikt и не делать разделение мод АГ на чётные и нечётные, то при каждом фиксированном p индекс q пробегал бы значения от 0 до p , соответствующие числа X q ( p , £ ) выстраивались по возрастанию, а моды

АГ допускали бы единообразное рассмотрение, подобное модам Эрмита - Гаусса, где, несмотря на наличие чётности-нечётности многочленов Эрмита, никто не расщепляет семейство мод ЭГ на соответствующие подсемейства. Тем не менее пока мы будем придерживаться устоявшихся обозначений.

Так как моды АГ структурно устойчивы, то в дальнейшем мы будем записывать их при z = 0, опуская аргумент z для краткости, но указывая явно зависимость от параметра £ : IG pp° ) ( r , z ) ^ IG pp° ) ( r ) ^ IG pq ) ( r , £ ). Такой вариант записи удобен при рассмотрении предельных случаев £ = 0 и £ = да, когда моды АГ сводятся к модам ЛГ и ЭГ соответственно. Кроме того, подобно формулам (6) мы будем использовать моды АГ при наличии и отсутствии нормировки:

I⁽ e ■ o ⁾ir £i

^IG- ⁾⁽ r , ^{£ )} = . r ), ⁽¹³⁾

предпочитая в тяжёлых случаях использовать вариант записи без нормировки, I peqo ) ( r , £ ), поскольку для мод АГ он, как правило, существенно проще нормированного.

2.    Разложение мод АГ по модам ЭГ и ЛГ при малых значениях p

Самый простой случай - это p = 0. Тогда q = 0 и чётная мода АГ - это стандартный Гауссов пучок:

IG 0,0 ( r , £ ) = HG 0,0 ( r ) = LG 0,0 ( r ).                 (14)

Следующие три моды также не зависят от параметра £ и были приведены в [4, 5]:

IG e ,1 ( r , £ ) = HG 1,0 ( r ) = V2Re LG 0,1 ( r ),

IG 0 ,1 ( r , £ ) = HG 0,1 ( r ) = V2 Im LG 0,1 ( r ),           (15)

IG 0 ,₂ ( r , £ ) = HG 1,1 ( r ) = T2Im LG 0,₂ ( r ).

• 2.1.    Случаи, когда характеристический многочлен – многочлен второй степени

Далее мы без вывода приведём явные аналитические выражения (табл. 1) тех мод АГ, когда характеристический многочлен оказывается многочленом второй степени и соответствующие корни X _q ( p , £ ) можно выразить в квадратных радикалах.

Следует отметить, что параметр £ (параметр эллиптичности), если отбросить первоначальное определение £ = 2 а ², вполне можно рассматривать как отрицательное число (это отмечал ещё Эдвард Айнс [18]). Поэтому мы добавим к предельным случаям мод АГ при £ = 0 и £ = да ещё и случай £ = - да.

Здесь коэффициенты a , b , c , d являются положительными, монотонно возрастающими функциями от £ :

a = £ + 4 £ ² + 1, b = £ - 1 + 4 ( £ — 1) 2 + 3, c = £ + 1 + 7 ( £ + 1)² + 3, d = ( £ + л/£~+ 9 )/з.

Табл. 1. Нормированные пучки АГ через суперпозиции двух пучков ЭГ или двух пучков ЛГ и их предельные случаи

	е^ - ^	е = 0	е^ +го
e ,        HG 2,0 ( r ) + a - HG 0,2 ( r ) _( a - 1)Re LG 0 ! 2 ( r ) + ( a /+ 1) LG^^ IG 2,0 ( r , е )                  /------ - i— I------- ,                   V1 + a 2                      V2-V1 + a 2	– HG 2,0 ( r )	LG 1,0 ( r )	– HG 0,2 ( r )
e Z ,     a - HG 20 ( r ) — HG 02 ( r ) ( a + l)T2Re LG 02 ( r ) — ( a — l) LG 1 0 ( r ) IG 2,2 ( r , е ) = +            1 =                      /------ ■                    v1 + a 2                           2 2 - V1 + a 2	– HG 0,2 ( r )	2Re LG 0,2( r )	+ HG 2,0 ( r )
_ e, ,     Л - HG 3,0 ( r ) + b - HG 1,2 ( r ) 73 ( b — 1)Re L^r ) + ( b + 3)Re LGu ( r ) IG 3,1 ( r ,е)             /о V3 + b 2                         V2 - V3 + b 2	– HG 3,0 ( r )	2Re LG 1,1( r )	– HG 1,2 ( r )
e        b - HG^r ) — V3 - HGu ( r ) ( b + 3)Re LG 03 ( r ) — V3( b — 1)Re LGu ( r ) IG3,3 ( r, е ) +               1 ------7                                    I- 1 ------7 V3 + b 2                            22 - V3 + b 2	– HG 1,2 ( r )	2Re LG 0,3( r )	+ HG 3,0 ( r )
_o, ч        - HG 2,1 ( r ) + c - HG p/ r ) ( c — 3)Im LG 03 ( r ) + V3( c + 1)Im LG 1,1 ( r ) IG 3,1 ( r , е )                    /                                               l~ 1 I V3 + c 2                           V2 - \3 + c 2	– HG 2,1 ( r )	2Im LG 1,1( r )	– HG 0,3 ( r )
o 7 4     c - HG 21 ( r ) — 73 - HG 03 ( r ) V3( c + 1)Im LG 03 ( r ) — ( c — 3)Im LG 11 ( r ) IG 3,3 ( r , е ) = +              /------.             =                     г~ I -----7 V 3 + c                          V2 - v 3 + c	– HG 0,3 ( r )	2Im LG 0,3( r )	+ HG 2,1 ( r )
_o ( ,    HG 3,1 ( r ) + d - HGu ( r ) ( d — 1)Im L^/r ) + ( d + 1)Im LG 1,2 ( r ) IG 4,2 ( r , е ) A 1 + d 2                        V1 + d 2	– HG 3,1 ( r )	2Im LG 1,2( r )	– HG 1,3 ( r )
o          d - HG 31 ( r ) — HG 13 ( r ) ( d + 1)Im LG 04 ( r ) + ( d — 1)Im LG 12 ( r ) IG4,4(r,е) = +           1 -----7         =                    /-----7 V1 + d 2                        V1 + d 2	– HG 1,3 ( r )	2Im LG 0,4( r )	+ HG 3,1 ( r )

Следует отметить сходство тех мод АГ, у которых одинаковы индексы p и флаги чётности-нечётности ( e , o ). Например, чтобы из моды IG 4,₂ ( r , е ) получить моду IG 4,₄ ( r , е ), достаточно поменять местами коэффициенты в суперпозиции и сменить знак у одного из них. Оказывается, аналогичное свойство справедливо и в более общем случае. А именно, если при фиксированных p и ( e , o ) известен весь набор мод АГ, за исключением какой-то одной, то эту последнюю моду можно получить, манипулируя коэффициентами разложения мод из набора. Когда характеристический многочлен является квадратичным, то мод всего две и «манипуляция» – это просто перестановка коэффициентов со сменой знака. Для более сложных случаев и манипуляции сложнее. Однако они несравнимо проще, нежели получение зависимости коэффициентов суперпозиции от параметра эллиптичности.

• 2.2.    Случаи, когда характеристический многочлен – многочлен третьей степени

Для мод IG 4,2 m ( r , е ), где m = 0,1,2, получается характеристическое уравнение

X 4 ( Х , е ) = X ³ - 20 X ² + 16(4 — e²)X + 192 е ² = 0,    (17)

корни которого X m ( е ) находятся с помощью формулы Кардано. В порядке возрастания:

где c4 = 3 413 + 3е2 cos ф, s4 = 3713 + 3е2 sinф, x 1 f 35 — 18е2 7 ф = — arccos--— .

3         7 (13 + 3 е ²)³² J

Для случая p =4 чётные моды АГ (без нормировки) имеют вид:

1 42m ( r , е ) = 32 { 2Re^ ( r ) — A Re 4,2 ( r ) +

⁺ A 4,0 ^{( r )} } = ⁽ A ⁺ A 1 ⁺ 1) ^ 4,0 ^{( r ) + (2} A ^{— 6) x    (19)}

^x ^ 2,2 ^{( r ) + (} A ^— A 1 ⁺ 1)%м( ^{г )}

где m = 0,1,2 и

.               (X m — 4)( X m — 16) ,

A = A )⁽ m , ^{е )} =----------- 1,

4 е ²

A = 4( m , е ) = ( X m — 16)/ е .

Мы не стали приводить нормированный вариант, чтобы избежать записи громоздких дробей, и приведём нормированные моды АГ только в предельных случаях (табл. 2).

^X 0 = "3-- ² c 4 ,

X e =-- + С 4 — S 4 73,

X 2 =-- + c 4 + s 4 73,

Табл. 2. Нормированные моды Айнса–Гаусса в предельных случаях при p = 4

	е^ - го	е = 0	Е^ + ГО
IG 4,0 ( r , е )	+ HG 4,0 ( r )	LG 2,0 ( r )	+ HG 0,4 ( r )
IG 4,2 ( r , е )	+ HG 2,2 ( r )	2Re LG 1,2 ( r )	– HG 2,2 ( r )
IG 4,4 ( r , е )	+ HG 0,4 ( r )	2Re LG 0,4( r )	+ HG 4,0 ( r )

Для компьютерного вычисления мод АГ, когда параметр эллиптичности не слишком мал и не слишком велик, следует использовать формулу Кардано и разложения (19), добавляя нормировочный множитель по необходимости. Если же параметр эллиптичности близок к предельным значениям, то выгоднее использовать асимптотические выражения характеристических корней. Например, при m = 2 и s^ 0 получаем

A =-114s2 + O(s4), A = 3s + O(s3), поэтому

I e4 ( r , s ) = 64 Re < 0,4 ( r ) - 32 s Re ^( г ) + O ( s ²).

Кроме того, можно показать, что между модами АГ, которые построены для параметров ε и –ε, существует простая взаимосвязь:

IG p ,2 m ( X , У , —s ) = ( — 1) m IG ep,2m ( У , X , s ),

IG p ,2 m ( x , y , -s ) = ( - 1) ^{m + 1} IG p ,2 m ( y , x , s ),            (20)

IG op ,2 m + 1 ( X , У , -s ) = ( - 1) ^m IG p ,2 m + 1 ( У , X , s ).

Здесь первые две формулы записаны для случая чётного p , а последняя – для нечётного p . Это ещё раз показывает, что случай отрицательных ε при исследовании мод АГ так же важен, как и случай положительных.

Основой для доказательства соотношений (20) является следующее свойство характеристических многочленов:

x Pe > o ) ( X , s ) = x Pe > o ) ( X , -s ), если p чётно, X op ( X , s ) = x p ( X , -s ), если p нечётно.

Рассмотрим случай p =5. Для чётных мод АГ получается характеристическое уравнение

X 5 ( X , s ) = X ³ - (35 + 3 s ) X ² + (259 + 102 s - 13 s ²) X - (22)

• - 225 - 675 s + 205 s ² + 15 s ³ = 0.

Опять применяем тот вариант формулы Кардано, когда кубическое уравнение имеет три вещественных корня, и записываем эти корни по возрастанию:

Для случая p =5 чётные моды АГ (без нормировки) имеют вид:

Is,2m + 1 ( г , s ) = 64/2 { 2Re 4,5 ( г ) - A Re 4з( г ) +

+ a Re 4,1 ( г ) } = ( A o + A 1 + WW +          (24)

+2(A0 - A -5)^3,2(г) +(A -3A1 + 5)^.,4(Г), где m = 0,1,2 и

. _ (X m - 9)( X m - 25) - 5

A 0            2 s ²          2,

A = X m - 25

s

Нормированные моды АГ в предельных случаях принимают вид, приведённый в табл. 3.

Табл. 3. Нормированные моды Айнса–Гаусса в предельных случаях при p = 5

	s ^ - ®	s = 0	E^ + W
IG 0 д( г , s )	+ HG 5,0 ( r )	2Re LG 2,1( r )	+ HG 1,4 ( r )
IG 5з ( г , s )	+ HG 3,2 ( r )	2Re LG 1,3( r )	– HG 3,2 ( r )
IG 5, ( г , s )	+ HG 1,4 ( r )	2Re LG 0,5( r )	+ HG 5,0 ( r )

Из (21) следуют соотношения между корнями характеристических многочленов: X m ( s ) = X m ( -s ). Поэтому в силу (20) нечётные моды АГ получаются из чётных перестановкой индексов мод ЭГ, заменой ε на –ε и добавочным множителем (–1) ^m :

Ч2 m+1(г, s) = 64^2 x x {2Im £0,5 (г) - B1 Im <1,3 (г) + B0 Im <2,1 (г)} = (25) = (B0 + 3 B1 + 5Ж1(г) +

+2(B0 + B1 - 5)%,3 (г) + (B0 - B1 +1)%,5 (г), где m = 0,1,2 и

( X m - 9)( X m - 25) 5

Ba = ,

⁰            2 s ²            2,

B = X m - 25

где

X 0

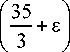
2 c 5 ,

X e

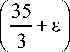
+ C 5

X 2

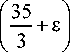
+ C 5 +

- s 5 V³,

s ₅ 3,

c ₅ = 3^28 - 6 s + 3 s ² cos ф ,

s ₅ = 3^28 - 6 s + 3 s ² sin ф ,

ф

= — arccos

80 + 9 s- 18 s ² 7 (28 - 6 s + 3 s ²) 3 ² J .

Остался ещё один случай, когда характеристическое уравнение является кубическим, – это случай p =6 для нечётных мод АГ:

x o ( X , s ) = X ³ - 56 X ² + 16(49 - s ² ) X - 384(6 - s ²) = 0. (26)

Тогда

X 0

X e

x 2

= 3"^{- 2 c} 6 ,

= 56 + c 6 - 3s St

= 56 + c 6 + 3sSt

где

c6 — -3 449 + 3s2 cos ф, s6 — 3^49 + 3s2 sinф, x 1 f 143 - 18s2

ф — — arccos--

3        ^ (49 + 3 s ²)³²

.

Соответственно, нечётные моды АГ (без норми-

ровки) примут вид:

^ 6,2 m + 2 ( r , s ) — 128 { 4Im Wr ) -

• - 2 B 2 Im £ 1,4 ( r ) + 2 B i Im £ 2,2 ( r ) } —

— 2( B 1 + 2 B 2 + 3) ^ ₅,₁ ( r ) +

+ 4( B 1 - 5)^ ,3 ( r ) + 2( B 1 - 2 B 2 + 3)% ,₅ ( r ),

где m = 0,1,2 и

B i =

( x m - 16)( x m - 36)

2 s ²

o     d _ x m - 36

• 3,    B 2 —--------

• s
2.3. Случай чётных мод АГ при p = 6

Рассмотрим случай p =6 для чётных мод АГ. Характеристический многочлен имеет четвёртую степень:

x 6 ( X , s ) — x ⁴ - 56 X 3 + 8(98 - 5 s ²) X ²

-

- 96(24 - 17 s ²) X - 144 s ²(96 -s ²) = 0.

Его корни X m ( s ) находятся с помощью формулы Феррари. Мы воспользуемся вариантом этой формулы, приведённым в [19]. Пусть

4        „    ~   ~ h — 3(49 + 5s2) + С6 + S6V3 -

вспомогательная величина, где

С 6 — 3^889 + 178 s ² + 13 s ⁴ cos ф ,

S6 — 3V889 + 178s2 + 13s4 sinф, x 1 f 24013 - 603 3s2 + 1317s4 + 3 5s6 ф — -arccos--------

3         ^        (889 + 178 s ² + 13 s ⁴)³/²

Тогда четыре корня уравнения (29) в порядке возрастания выражаются через h следующим образом:

Тогда моды АГ (без нормировки) выражаются через моды ЛГ и ЭГ следующим образом:

Ilim ( r , s ) — 128 { 4Re 4,6 ( r ) - 2 A 2 Re 4,4 ( r ) +

+ 2 A 1 Re £ 2,2 ( r ) - 3 44,o ( r ) } — ( A + A 1 + A 2 + 1) * x^ ,o ( r ) + (3 A o + A 1 - 5 A 2 - 15M 2 ( r ) +          (31)

+ (3 A o - A 1 - 5 A 2 + 15) ^ 2,4 ( r ) +

+(Ao - A1 + A2 - 1)^o,6(r), где m = 0,1,2,3 и

( X m - 4)(x m - 16)(x m - 36) - 4(x m - 24) 12 s ³                   3 s

( x m - 16)( x m - 36) - 3     A 2 _— x m - 36

Нормированные моды АГ в предельных случаях принимают вид, указанный в табл. 4.

Табл. 4. Нормированные моды Айнса–Гаусса в предельных случаях при p = 6

	s^ - и	s = o	E^ + и
IG 6,o ( r , s )	– HG 6,0 ( r )	LG 3,0 ( r )	– HG 0,6 ( r )
IG 6,2 ( r , s )	– HG 4,2 ( r )	2Re LG 2,2( r )	+ HG 2,4 ( r )
IG 6,4 ( r , s )	– HG 2,4 ( r )	2Re LG 1,4 ( r )	– HG 4,2 ( r )
IG 6,6 ( r , s )	– HG 0,6 ( r )	2Re LG 0,6 ( r )	+ HG 6,0 ( r )

2.4. Численные методы и моды АГ

Известно, что у всех характеристических многочленов x P³ , o ) ( X , s ), независимо от величины p и флага чётности ( e , o ), коэффициент при любом слагаемом вида X^vs^M является целым числом. Поэтому асимптотические разложения корней X m , ^o ) ( s ) по степеням £ (и при s^ o , и при е^± и ) будут иметь в качестве коэффициентов разложения рациональные числа (см. формулы, приведённые ранее, как примеры таких разложений). Как следствие, если записать асимптотические разложения мод АГ по модам ЛГ и ЭГ, то коэффициенты таких разложений представимы в виде рядов по степеням £ (если s^ o , то по степеням £, £² и т.д.; если s^± и , то по обратным степеням), и коэффициенты в этих рядах также рациональны.

Рассмотрим пример. Возьмём моду IG _{3 4}( r , s ) и запишем её в виде:

X 0 — 14 - hh - 4(49 + 5 s ²) - h - ^{64(9 2 s} 2 ) , h

X ^f — 14 - hh + /4(49 + 5 ё ^ ) - h — 64(9 - 2 ^s 2 ⁾, ^h ₂ (30)

X 2 — 14 + hh -. 4(49 + 5 s ²) - h + ⁶⁴⁽⁹ 2^s") , h

X 3 — 14 + hh + (4(49 + 5s² ) - h + 64(9 -l^s^⁾ . h

IG f ,1 ( r , s ) —

— 1 . (Ao + 1M,o(r) + (Ao - 3Ж,2(г)(32)

2V2n     7(Ao +1)23 + (Ao - 3)2.

Здесь

2^ —| ^,2 ( r )|| — 4|£ 1,1 ( r )|| и

X o - 9   - 4 + s- 2^4 - 2 s+ s ²

Ao —-----—------------------- ss

.

Ограничиваясь в коэффициентах разложений при £^ 0 и s^± да только членами до £ 3 и в^{- 4} соответственно, получим следующие асимптотики.

Если s ^ 0 , то

IG 3 ,i ( r , s ) =

242 П

^^^^^^.

1 s 7 s ² 11 s ³ +---1---1--

2 16 256 2048

^(r) + (33)

( 1 3 s 9 s ² 15 s ³ +

^ 2 16 256 2048

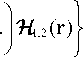
В частности, поскольку

- 2 { ^ 3,o ( r ) + Ч2 ( r ) } = 4^2 Re 4,1 ( r ),

то как предельный случай получаем равенство, которое уже хорошо известно: IG 3 ,1 ( r ,0) = 22 Re LG 1,1 ( r ).

Если s ^ ± да , то

Рис. 1. Распределения интенсивности мод IG31(r, s) (первый ряд сверху), IG3,3(r, s) (второй ряд), IG34(r, s) (третийряд), IG3,3(r,s) (четвертыйряд) при некоторых значениях параметра ε (ε = –20 – столбец 1, ε = –3 – столбец 2, ε = –1 – столбец 3,ε = 0 – столбец 4, ε = 1 – столбец 5, ε = 3 – столбец 6, ε = 20 – столбец 7); длина волны λ = 532 нм, радиус перетяжки Гауссова пучка w0 = 1 мм. Масштабная метка обозначает 1 мм

^{IG 1 lt r} ’ ^{s )} = Ж*

К 1 1 , 1 , 19 , ^

x11+%!(r) + к 2s 2s2 16s3 16s4 J 3,0

Г 3     3     45               1

+ - 1 +    +    + -⁴ 5- + % ₂(r) .

^      8 s ² 4 s ³ 128 s ⁴      J ² J

Здесь в предельном случае получается мода ЭГ: ^IG 3’1 ^{( r} , “ ) = ^{- H}G 1’2 ^{( r )} .

3.    Моделирование

В этом параграфе приводятся распределения интенсивности пучков АГ разного порядка и для разных значений параметра ε, рассчитанные путём решения характеристического уравнения и разложения по модам ЛГ. При расчете были использованы выражения (19), (24), (25), (28) и (31), а также табл. 1.

• 3.1.    Расчёт пучков Айнса–Гаусса при p = 3

• 3.2.    Расчёт пучков АГ при p = 4

На рис. 1 показаны распределения интенсивности пучков АГ при p =3 и разных значений параметра ε.

Рис. 1 подтверждает, что при малых значениях параметра £ ( s® 0) мода IG 1 ,3 сводится к Re LG ₀,₃ , амплитуда которой пропорциональна cos 3φ, то есть интенсивность содержит шесть лепестков, лежащих на одном светлом кольце. Также рис. 1 подтверждает, что интенсивность нечётной моды IG 3 ^o ,3 также содержит шесть лепестков, но повёрнутых на угол π/6.

Также рис. 1 подтверждает, что картина интенсивности у чётного пучка IG ^e 3,1 при малом параметре ε имеет два лепестка и кольцо, разорванное на две дуги, вытянутые вдоль вертикальной оси. Соответственно у нечётного пучка IG 3 ^o ,1 интенсивность при малом параметре ( s® 0) также имеет два лепестка, разрывающие два светлых кольца, но вытянутые вдоль горизонтальной оси.

При больших значениях параметра в ( s >> 1) моды АГ определяются модами ЭГ и имеют декартову симметрию. Видно, что при s >> 1 чётная мода IG 3,1 совпадает по интенсивности с модой ЭГ HG 1,2 и имеет 6 локальных максимумов, а мода IG ^e 3,3 совпадает с модой ЭГ HG 3,0 и имеет 4 лепестка, лежащих на горизонтальной оси. У нечётных мод при s >> 1, наоборот, мода IG 3 ^o ,1 имеет 4 лепестка, лежащих на вертикальной оси, а мода IG 3 ^o ,3 имеет 6 лепестков, разделённых двумя вертикальными и одной горизонтальной нулевой линиями.

На рис. 2 показаны распределения интенсивности пучков АГ при p = 4 и разных значений параметра ε.

Из рис. 2 видно, что, действительно, при малом значении ε моды АГ совпадают с соответствующими модами ЛГ: у пучка IG ^e 4,0 интенсивность имеет центральное световое пятно и окружающие его два световых кольца, у пучка IG ^e 4,2 интенсивность имеет по четыре лепестка, лежащих на двух кольцах. У пучка IG ^e 4,4 интенсивность имеет 8 лепестков, лежащих на кольце, а у пучка IG ^o 4,2 интенсивность имеет 8 лепестков, лежащих по четыре на двух кольцах. У пучка IG 4 ^o ,4 интенсивность имеет 8 лепестков, лежащих на одном кольце.

Также рис. 2 подтверждает, что при больших положительных значениях параметра ε пучки АГ совпадают с пучками ЭГ. Поэтому картины интенсивности пучков АГ при s >> 1 совпадают с соответствующими пучками ЭГ. У пучка IG ^e 4,0 интенсивность имеет 5 лепестков, лежащих на вертикальной оси и разделённых четырьмя горизонтальными линиями нулей интенсивности; у пучка IG ^e 4,2 интенсивность содержит 9 лепестков, разделённых 2 горизонтальными и 2 вертикальными линиями нулевой интенсивности; у пучка IG ^e 4,4 интенсивность имеет

5 лепестков, лежащих на горизонтальной оси и разделённых четырьмя вертикальными линиями нулей интенсивности; у пучка IG4o,2 интенсивность имеет 8 лепестков, разделенных одной вертикальной и 3 горизонтальными линиями нулей интенсивности, и у пучка IG4o,4 интенсивность такая же, как у пучка

(первый ряд), IG e 4,2 ( r , ε ) (второй ряд), IG e 4,4 ( r , ε ) (третий ряд), IG 4 o ,2 ( r , ε ) (четвёртый ряд), IG o 4,4 ( r , ε ) (пятый ряд) при следующих параметрах: длина волны λ = 532 нм, радиус перетяжки Гауссова пучка w 0 = 1 мм, при некоторых значениях параметра ε (ε = –20 – столбец 1, ε = –3 – столбец 2, ε = –1 – столбец 3, ε = 0 – столбец 4, ε = 1 – столбец 5, ε = 3 – столбец 6, ε = 20 – столбец 7).

Масштабная метка обозначает 1 мм

• 3.3.    Расчёт пучков АГ при p = 5

• 3.4.    Расчёт пучков АГ при p = 6

На рис. 3 показаны распределения интенсивности пучков АГ при p =5 и разных значений параметра ε.

Из рис. 3 видно, что так же, как и при меньших значениях p , при малом значении параметра ε моды АГ совпадают с вещественными и мнимыми частями мод ЛГ, а при большом по модулю значении параметра ε моды АГ сводятся к одной из мод ЭГ.

На рис. 4 показаны распределения интенсивности пучков АГ при p =6 и разных значений параметра ε.

Рис. 4 подтверждает, что при малых значениях параметра эллиптичности ε интенсивность моды IG ^e 6,0 имеет центральное пятно и три светлых кольца, интенсивность моды IG ^e 6,2 имеет по 4 лепестка на трёх светлых кольцах, интенсивность моды IG ^e 6,4 имеет по 8 лепестков на двух светлых кольцах, а интенсивность моды IG ^e 6,6 имеет 12 лепестков на одном светлом кольце. Картина интенсивности моды IG 6 ^o ,2 совпадает с интенсивностью моды IG ^e 6,2 , повернутой на π/4, картина интенсивности моды IG 6 ^o ,4 совпадает с интенсивностью моды IG ^e 6,4 , повернутой на π /8, и картина интенсивности моды IG 6 ^o ,6 совпадает с интенсивностью моды IG ^e 6,6 , повернутой на π /12.

Рис. 3. Распределения интенсивности мод IG e 5,1 ( r , ε ) , IG ^e 5,3 ( r , ε ) , IG 5 ^e ,5 ( r , ε ) (ряды 1 – 3), IG 5 ^o ,1 ( r , ε ) , IG 5 ^o ,3 ( r , ε ) , IG 5 o ,5 ( r , ε ) (ряды 4 – 6) при следующих параметрах: длина волны λ = 532 нм, радиус перетяжки Гауссова пучка w 0 = 1 мм, при некоторых значениях параметра ε (ε = –20 – столбец 1, ε = –3 – столбец 2, ε = –1 – столбец 3, ε = 0 – столбец 4, ε = 1 – столбец 5, ε = 3 – столбец 6, ε = 20 – столбец 7). Масштабная метка обозначает 1 мм

Рис. 4. Распределения интенсивности мод IG e 6,0 ( r , ε ) , IG ^e 6,2 ( r , ε ) , IG ^e 6,4 ( r , ε ) , IG ^e 6,6 ( r , ε ) (ряды 1 – 4), IG 6 ^o ,2 ( r , ε ) ,

IG 6 o ,4 ( r , ε ) , IG 6 o ,6 ( r , ε ) (ряды 5 – 7) при следующих параметрах: длина волны λ = 532 нм, радиус перетяжки

Гауссова пучка w 0 = 1 мм, при некоторых значениях параметра ε (ε = –20 – столбец 1, ε = –3 – столбец 2, ε = –1 – столбец 3, ε = 0 – столбец 4, ε = 1 – столбец 5, ε = 3 – столбец 6, ε = 20 – столбец 7). Масштабная метка обозначает 1 мм

Рис. 4 также подтверждает, что при больших положительных значениях ε моды АГ совпадают с соответствующими модами ЭГ. Поэтому интенсивность моды IGe6,0 имеет 6 горизонтальных линий нулевой интенсивности, мода IGe6,2 имеет 2 вертикальные и 4 горизонтальные линии нулевой интенсивности, мода IG e6,4 , наоборот, имеет 4 вертикальные и 2 горизонтальные линии нулевой интенсивности. Интенсивность моды IG e6,6 такая же, как у моды IG e6,0 , но повернутая на π/2. Интенсивность моды IG6o,2 имеет одну вертикальную и 5 горизонтальных линий нулевой интенсивности, интенсивность моды IG6o,4 имеет 3 горизонтальных и 3 вертикальных нулевых линии, и, наконец, интенсивность моды IG6o,6 совпадает с интенсивностью моды IG6o,2 , но повёрнута на π /2.

Заключение

В этой работе получены аналитические выражения для 24 мод АГ с индексами p =3, 4, 5, 6 через 2, 3 или 4 моды ЛГ (точнее, через их вещественные или мнимые части) и ЭГ (см. выражения (19), (24), (25), (28), (31) и табл. 1). Коэффициенты разложения мод АГ по модам ЛГ и ЭГ выражены через параметр эллиптичности ε. Из полученных выражений сразу следуют выражения для мод АГ при значениях параметра ε, равных нулю или плюс (минус) бесконечности. Явная зависимость мод АГ от параметра эллиптичности позволяет управлять их интенсивностью, меняя этот параметр. Получены свойства симметрии для четных и нечетных мод АГ, в том числе показано, как связаны эти моды между собой при смене знака у параметра эллиптичности. Полученные представления мод АГ через моды ЭГ и ЛГ не только удобны с теоретической точки зрения, так как помогают без моделирования видеть свойства этих пучков, но и с практической точки зрения, позволяя довольно легко программировать амплитуды мод АГ для моделирования или для их формирования с помощью пространственного модулятора света.

Работа выполнена при поддержке Российского научного фонда (грант № 22-12-00137) в частях теории и моделирования и по государственному заданию НИЦ «Курчатовский институт» в частях «Введение» и «Заключение».