В оптике известны лазерные пучки, которые описываются скалярными комплексными амплитудами, являющимися точными решениями непараксиального уравнения Гельмгольца. Это хорошо известные плоские и сферические волны [1], а также полученные недавно моды Бесселя [2], пучки Матье [3] и параболические лазерные пучки [4]. В работе авторов [5] были рассмотрены непараксиальные гипергеометрические (нГГ) лазерные пучки. Они тоже являются решением уравнения Гельмгольца и получены на основе вычисления интеграла для углового спектра плоских волн только для чётных номеров топологического заряда спиральной фазы пучка. Эти нГГ-пучки описываются комплексной амплитудой в виде произведения двух функций Куммера 1 F 1 ( a , b , x ) [6] с разными аргументами x . Они представляют собой суперпозицию двух одинаковых световых волн, распространяющихся в положительном и отрицательном направлениях оптической оси z . В [5] также с помощью асимптотического разложения одной из функций Куммера получены приближённые выражения для комплексной амплитуды, описывающей прямую и обратные световые волны (гипергеометрические лазерные пучки).

В данной работе мы обобщили результаты работы [5] и получили точное решение уравнения Гельмгольца для любого целого номера топологического заряда, описывающее непараксиальный лазерный пучок, комплексная амплитуда которого представляет собой произведение функции Куммера 1 F 1 ( a , b , x 1 ) и второго решения уравнения Куммера U ( a , b , x ₂). Так как при определённых параметрах функция U ( a , b , x ₂) пропорциональна функции Хан-келя, а функция Куммера – функции Бесселя, то такие пучки названы непараксиальными пучками Ханкеля-Бесселя. Заметим, что полученного решения нет в справочниках специальных функций [6,7] и в известной работе Миллера [8].

Пучки Ханкеля-Бесселя (n =0) порождаются источником в начальной плоскости с бесконечной плотностью энергии. При распространении вдоль положительной оси z эти пучки расходятся пропорционально z . При ненулевом топологическом заряде n порождающий источник не излучает вдоль оптической оси.

1. Решение уравнения Гельмгольца в параболических координатах

Рассмотрим уравнение Гельмгольца в цилиндрических координатах ( r , φ, z ):

( д2 1 д X д2 д2 k2)

(дr2 + r дr + r2 дф2 +дz2 + J Х х E (r, ф, z ) = 0, где k – волновое число.

Будем искать решение E ( r , φ, z ) в следующем виде:

E (r, ф, z) = E (r, z) rp exp (inф + ikz).(2)

Тогда для E ( r , z ) получим уравнение:

д ² E д ² E ( 2 p + 1 ) д E

—2- + —2- +1I— +

д r    дz   ^ r ) д r

+ 2 ik — + ( ^P ”_г n | E = 0.

д z ( r )

При p = ± n последнее слагаемое в (3) пропадает. Перейдём к параболическим координатам:

x = z + V r2 + z2, y = z - V r2 + z2.

В параболических координатах (4) уравнение (3) примет вид (при p = + n ):

д ² E x д x²

д ² E y ^^{+ д} У

+ (n +1 + ikxA ^- - (n +1 + iky) — = 0.

(           )дx (           )дy

Уравнение (5) решается в разделяющихся переменных. Подставив в (5) E ( x , y )= X ( x ) Y ( y ), получим:

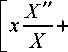
^{( n + 1 +} ikx ) — =

Y" , J 1 yy ⁺( ^{n + 1 +} iky ) Y

= C ,

где C – постоянная, не зависящая от x и y . Тогда вместо уравнения (5) будем иметь два уравнения:

x —;—+ (n +1 + ikx)--CX — 0,

< dx2 v 1 dx d2Y (   1 i idY ™ л y—7- + (n +1 + iky)--CY — 0.

d y ^{2 v 7}d y

Обозначив £ = - ikx , n = - iky и C =- ikD , оба уравнения (7) преобразуются в уравнения Куммера:

Оно описывает стоячую волну, образованную в результате интерференции двух одинаковых волн, распространяющихся в положительном и отрицательном направлениях оптической оси z .

Это следует из того, что для больших расстояний z ≫ r , используя приближённые выражения для функции Бесселя от малых и от больших значений аргумента, выражение (12) приближённо равно следующему:

E ( r , ф , z ) — E ₀ Г ^ 1 + 2 exp ( in ф ) х

n(13)

• 2 । 2 kr ² । ²      Г,n

• x. -----1------I cos kz,

V п kz ^ z J     (     44

' ^ d'/+(n+1 -^ f- DX—0, i n^ + ( n +1 -n)^-DY — 0, dn           dn

решением которых будут являться функции Куммера 1 F 1 ( a , b , z ) [6]:

откуда видно, что амплитуда пропорциональна косинусу от расстояния.

Разделим световое поле (10) на прямые и обратные волны. Для этого воспользуемся связью функции Куммера M ( a , b , x ) = ₁ F ₁( a , b , x ) со вторым решением уравнения Куммера [6]:

X (5) — 1F1 (D, n +1, 5), Y (n)— 1F (D, n +1, n).

U (a, b, z) — —П—x sin п b

x

M ( a , b , z )        1 - _bM ( 1 + a - b ,2 - b , z )

Г ( 1 + a - b ) Г ( b ) ~ z     Г ( a ) Г ( 2 - b )

Тогда

X ( x ) — 1 F 1 ( D , n + 1, - ikx ) ,

Y (y)— 1 F( D, n + 1, - iky), а решение исходного уравнения Гельмгольца (1) теперь можно записать в следующем виде:

Функция (14) определена также и при целых значениях параметра b [6].

Обратив (14), получим выражение для ₁ F ₁( a , b , x ) через U ( a , b , x ):

• 1    F 1 ( a , b , z ) — AU ( a , b , z ) + BU ( b - a , b , - z ) ,    (15)

где

E ( r , ф , z ) — E ₀ ( kr ) n exp ( in ф + ikz ) x X 1 F 1 ( D , n + 1, x ₊ ) 1 F 1 ( D , n + 1, x _ ) ,

где x ±

- ik ( z ± 4r ² + z ² ) , E ₀ - постоянная, характе-

ризующая мощность пучка.

Это решение без вывода приведено в [8]. В частном случае при D =( n + 1)/2, используя выражения для функций Бесселя через функции Куммера [6]:

Г( b)

A — / ⁽ ) a D , Г ( b - a )

Г ( b),

B = r^ ^'eD,

D —        sin п b sin п(b - a) + (-1)b sin пa

.

.F I v + — ,2 v + 1,2 iz

¹¹ ( 2

/ X - v

I z I ^{— r}( 1 + ^v ) exp ( ⁱz ) 1 2 J Jv ( z ) ,

Используя (15), (16) и пренебрегая постоянными множителями, получим решение уравнения Гельмгольца (10) в следующем виде:

E (r, ф, z) —

— E ₀ ( kr ) n exp ( 1п ф )

из (10) можно получить

exp ( ikz ) Г ( n + 1 - D )

E ( r , ф , z ) — E ₀ Г ² 1 1 + n I ( 4 i ) n exp ( in ф ) x

^x Jn ^k ( z ⁺ V r 2 ⁺ z 2

2 L ²

) J. k ( -■ - r^ ) J 2 ^{L 2}                      .

UJ (D, n + 1, x+) 1 F( D, n + 1, x_) + n+1 exp (- ikz)

+ ( - 1 ) -- r^x

V 7 Г D

Решение (10) не описывает лазерное излучение, распространяющееся в определённом направлении.

x U ( n + 1 — D , n + 1, — x ₊ ) 1 F ( n + 1— D , n + 1, — x _ ) J .

Обозначив D = ( n + p +1)/2 и умножив обе части на Г ( D ) Г ( n + 1 - D ), получим:

E ( r , ф , z ) = i ² n ^{+ 1} E ₀ ( kr ) n exp ( in ф ) х

г f ^{n + e + 1} )    I  Vrf ^{n + e + 1}

- i ГI--- 2 I exp ( ikz ) U I---2—

, n ⁺ 1, x + I 1 F i

fn + в + 1

I 2

, n + 1, x — I +

fn -P + 1)   ₍ f n -P + 1

+ ¹ ГI 2 I exp ( - ikz ) U I 2

, n + 1, - x ₊ I ₁ F ₁

n -P+ 1    ,

2 , n ⁺ 1, ^- x

Данное выражение представляет собой сумму прямого и обратного гипергеометрических пучков, на что указывают показатели экспонент exp( ±kz ) в (18). Далее будем рассматривать прямые пучки, распространяющиеся от плоскости z = 0 в полупространство z >0. Выражение для прямого пучка имеет следующий вид:

страняется вдоль положительного направления оси z , следует из асимптотики функции Ханкеля 1-го рода при больших z ( kz » 1) [6, выражение 9.2.3]:

H z )

z

-

п v п

2 4

n „fn + в + 1 ^

^E + ( r , ф , z ) = (^{- 1} ) ^ГI —2— I ^х

х E ₀ ( kr ) n exp ( in ф + ikz ) х

В выражении (23), в отличие от (13), зависимость от расстояния включает в себя экспоненту вместо косинуса.

При n = 0 на оптической оси ( r = 0) интенсивность равна

f n + в + 1 x U   —

I 2

, n + 1, x ₊

FfИ +Р+1

¹¹ 1 2

, n + 1, x

I ( r = 0, ф , z ) =

i 5 E 0 H 01 ⁾( kz )

При n ^ 0 комплексная амплитуда такого поля на оптической оси ( r = 0) равна нулю, в то время как при n = 0 амплитуда отлична от нуля:

= 54- E 0 ² [ J 0 ² (fe) + Y   kz ) ] ,

En = 0 ( r = 0, ф , z ) = Г f в^ ) E 0 U f ^в 2 ' ,1, - 2 ikz ) .   (20)

В частности, при в = 0 выражение для прямого пучка (19) примет вид:

E ₊ ( r , ф , z ) = i^{3n + 1 П} Г ( n + 1 ) E ₀ exp ( in ф ) х

х H

( 1 ) ГI ₍ z + 7

n

r ² + z ²

) Jn

J 2 -

j ( 477?

-

z ) .

В начальной плоскости ( z = 0) аргументы и функции Ханкеля, и функции Бесселя равны kr /2. Функция Ханкеля расходится при стремлении аргумента к нулю. Используя приближённые выражения для функций Ханкеля и Бесселя при малых значениях аргумента [6, выражения 9.1.7, 9.1.9], можно показать, что при n ^ 0 и r = z = 0 амплитуда поля имеет конечное значение:

. ( - i ) n

E ₊ ( r = 0, ф , z = 0 ) =-----Г ( n + 1 ) E ₀ exp ( in ф ) .    (22)

n

Из (21) видно, что комплексная амплитуда непараксиального ГГ-пучка при в =0 пропорциональна произведению функций Ханкеля и Бесселя целых и полуцелых порядков. Поэтому световые пучки (18) и (21), чтобы их отличать от световых пучков, полученных в [5], будем называть пучками Ханкеля-Бесселя (ХБ). Из (21) видно, что ХБ-пучок не является модой свободного пространства, так как аргументы функций Ханкеля и Бесселя имеют разную зависимость от переменных r и z , и поэтому значения этих функций остаются постоянными при разных r при одинаковом z . То, что пучок (21) распро-

а максимум интенсивности достигается в точке z , удовлетворяющей уравнению

J ₀ ( kz ) J 1 ( kz ) + Y ₀ ( kz ) 3 1 ( kz ) = 0.                (25)

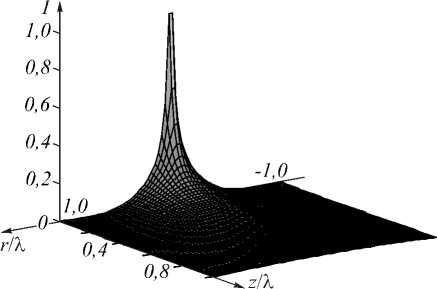
Моделирование показало, что функция f ( t ) = J ₀( t ) J 1 ( t ) + У ₀( t ) Y 1 ( t ) никогда не достигает нуля при t > 0, поэтому фокусировки такого пучка не происходит, происходит только спад интенсивности вдоль оптической оси вследствие расхождения пучка. Более того, в точке z = 0 функция (24) обращается в бесконечность, и в этом смысле поле (21) порождается точечным источником с бесконечной плотностью энергии, расположенным в начале координат. На рис. 1 показаны квадрат модуля функции (21) при z > 0: в плоскости Orz (рис. 1 а ), а также зависимости вдоль продольной оси z (рис. 1 б) и вдоль поперечной оси r (рис. 1 в ). Из (21) видно, что ХБ-пучки имеют бесконечную энергию.

Из рис. 1 в видно, что, несмотря на бесконечное значение в точке r = z = 0, функция (21) имеет строгий ноль. Из формулы (21) следует значение нуля r о = 0,76 % . Это позволяет говорить, что поле (21) порождается источником с бесконечной плотностью энергии и радиусом 0,76 % ( n = 0).

Рассмотрим другой частный случай, когда в = 1. Тогда выражение для прямого пучка примет вид:

^E + ( ^r , ф , ^z ) = (^- i ) n

^Г( n )

nE ₀ k ^{1 -} n

exp ( in ф ) r х

х

^Jn - 1

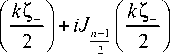
iH ( 1 ¹)!

n - 1

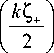
+ Я ( 1 )

^{+ 11} n + 1

где Z ± = ( z 2 + r 2 ) ¹/² ± z . Из (23) видно, что пучок (26) также распространяется вдоль положительного направления оси z .

E ₊ ⁽ г , ^ф , z ) = E о exp⁽ in ^{ф )} H ™⁽ kz ) J /2

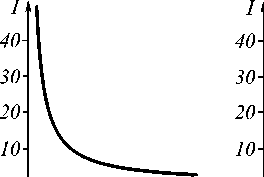
б)                                  в)

Рис. 1. Квадрат модуля функции (21) в плоскости Orz при n = 0, E0 = 100 (а), зависимость интенсивности от продольной координаты при r = 0 (б) и от радиальной координаты при z = 0 (в)

ления из начала координат в эту точку (рис. 2). На рис. 2 а показан квадрат модуля функции (21) (при n = 1, E 0 =100) в области размером 2 1x1 (белый цвет – ноль, чёрный цвет – максимум). На рис. 2 б-г показаны радиальные сечения интенсивности в плоскостях z = 0,1 1 , z = 0,01 1 , z = 0,001 1 .

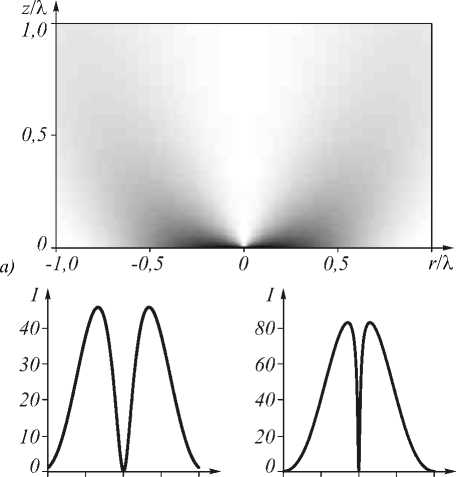
б)                                  в)

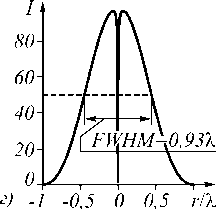
Рис. 2. Интенсивность в плоскости Orz при n = 1, E₀ = 100 (- Л < x < Л , 0 < z < Л , белый цвет - ноль, чёрный цвет -максимум) (а); радиальные сечения квадрата модуля функции (21) в разных плоскостях z = 0,1 Л (б), z = 0,01 Л (в), z = 0,001 Л (г)

• 3.    Частные случаи пучков Ханкеля-Бесселя

  г =

  
  
  
  
  
  

  где γ – постоянная, не зависящая от z . Функция Хан-келя, входящая в (21), расходится при стремлении аргумента к нулю, но такое возможно при одновременно малых значениях r и z . В этом случае аргумент функции Бесселя в (21) также стремится к нулю. Используя приближённые выражения для функций Ханкеля и Бесселя при малых значениях аргумента, можно показать, что

  
  

  При нечётных значениях n функции Бесселя по-луцелого порядка становятся элементарными. Рассмотрим частный случай при n = 1. В этом случае:

  
  

  2 i

  EK = 1 ( ^г , Ф , ^z ) = -j-E 0 exp ( i ф ) kr

  
  

  ^x sin 2 (v ^{г 2} + z ² — z

  
  

  x

  
  

  ) exp ik ( z + ^) .

  
  
  
  

  E + ( ^г , ф , ^z ) =

  
  

  ( - i ) ^K

  n

  
  

  Г ( n + 1 ) exp ( in ф ) tan ^K

  
  
  
  
  

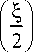
  Несмотря на то, что r находится в знаменателе (30), при r =0 на оптической оси будет нулевая амплитуда. Это можно показать, считая r ≪ z :

  lim En = 1 ( ^г , Ф , z ) =

  г ^ 0

  
  

  где tan £ = г / z . Т.е. амплитуда поля в некоторой точке, близкой к началу координат, зависит от направ-

  
  

  - 2 i

  = —j— E ₀ exp ( i ф + ikz ) lim

  
  

  1 sin

  r

  
  

  ) k!² )

  I 4 z J

  
  

  = 0.

  
  
  
  

Поле (30) формируется при следующем распределении амплитуды в начальной плоскости (в перетяжке):

En = 1 ( r , Ф , z = ⁰ ) =

- 2 i       (kr )     (ikr . )                  ⁽³²⁾

=--- E_n sin exp + i ф .

kr V 2 ) V 2      )

Диаметр перетяжки этого пучка FWHM =0,93 % (рис. 2 г ).

Амплитуда вблизи центра начальной плоскости равна E_n = 1 ( r = 0, ф , z = 0 ) = - iE ₀ exp ( i ф ) , а в самой центральной точке не определена из-за винтовой фазовой особенности, зато интенсивность при r = z =0 отлична от нуля I = | E_{n =1}( r = 0, ф , z = 0)| ² = | E ₀| ² .

При больших расстояниях z ≫ r (30) примет вид:

En=1 ( r, ф, z » r ) =

- 2 i       ( kr ² )

=--- E _o sin       exp ( i ф+ ikz ) .

kr ⁰ I 4 z )

• 4.    Результаты моделирования

На рис. 3 показаны результаты моделирования поля (30) для длины волны % = 633 нм: интенсивность и фаза в поперечной плоскости z = 2 % .

На рис. 4 показаны радиальные сечения интенсивности в плоскостях z = 2 % , z = 4 % и z = 6 % .

-4-

б)

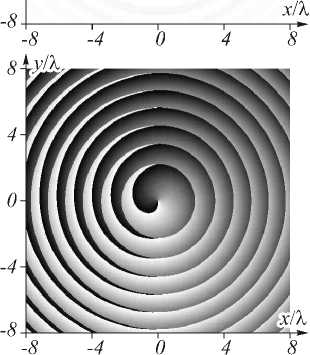
Рис. 3. Результаты моделирования пучка (30) для длины волны X = 633 нм: интенсивность (а) и фаза (б) в поперечной плоскости z = 2 X

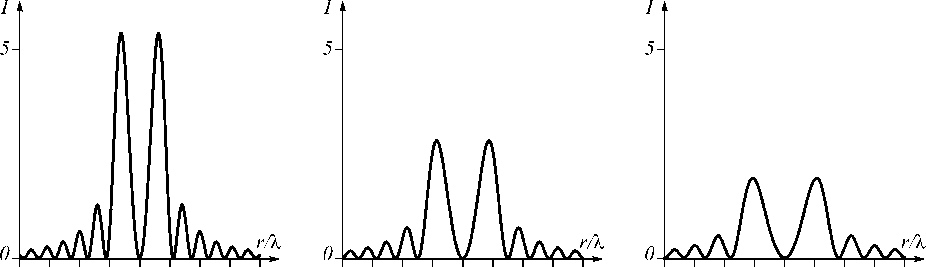
Рис. 4. Сечения интенсивности в плоскостях z = 2 X z = 4 X z = 6 X полученные по формуле (21) при n = 1, E₀ = 100

Для сравнения было проведено моделирование конечно-разностным FDTD-методом (рис. 5). При моделировании использовались следующие параметры: размер расчётной области: [-8%,8%] х [-8%,8%] х [0,8%]. Шаг дискретизации по всем координатам - %/16. Время моделирования – 20 периодов. Шаг дискретизации по времени - %/32. На рис. 5а показана усреднённая по времени интенсивность в плоскости z = 2%, а на рис. 5б, в - её радиальные сечения. Видно, что в центре интенсивность не спадает до нуля, что можно объяснить наличием продольной составляющей Ez (так как n = 1). Также видно, что интенсивности, показанные на рис. 4а и 5в, сходны по своей структуре, в то время как интенсивность на рис. 5б отличается и не спадает до нуля между светлыми кольцами. Это объясняется продольной со- ставляющей и линейной поляризацией, учитываемой при моделировании FDTD-методом и не учитываемой в скалярной теории.

• 5.    Фокусировка пучков Ханкеля-Бесселя

Сделаем в (21) замену переменной z ^ f - z (f - фокусное расстояние):

E+(r, ф,z ) =

= i^{3n + 1}2 Г ( n + 1 ) E ₀ exp ( in ф ) х

хHn1’ kff-z + Vr2 +(z-f) 2 L 2 V

х

- k 2 /      2\² r 1

n I Vr+( z - f ) - f + z) .2 L 2 V                     A

а)

б)

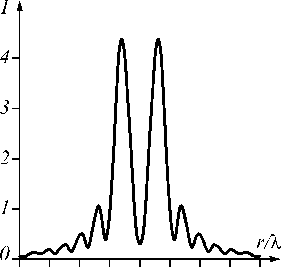
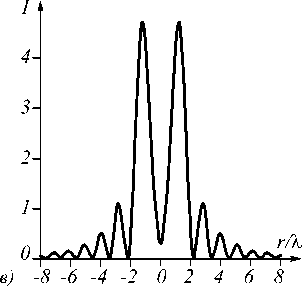
Рис. 5. Результаты моделирования распространения пучка Ханкеля-Бесселя с n = 1 конечно-разностным FDTD-методом (ТЕ-поляризация, Ex * 0): усреднённая по времени интенсивность в плоскости z = 2 1 (а), её горизонтальное (б) и вертикальное (в) сечения

При n = 0:

i пЕ0

^Еп = 0 ( r , Ф , z ) = 2" ^X

дит. Это можно объяснить тем, что при z >  f для точек вблизи оси, т.е. r <<  z – f , можно записать:

k

X H 01 -

8-

X

X J0

k (                       J

2(Vr +(z-f)-f+zJ

При z >  f и r =0 аргумент функции Ханкеля обращается в нуль и интенсивность становится бесконечной. В начальной плоскости z =0 такое поле имеет вид:

En=0 (r, Ф, z = 0) = ^ X

XH01) [ k (f +      2)

а)

z/X

з/Х

6-

4-

2-

-4

8 x/X

8~

При его задании в программе FullWAVE получается распространение поля, модуль амплитуды E x которого показан на рис. 6 а . На рис. 6 б показана усредненная по времени интенсивность в плоскости Oxz . При моделировании использовалась длина волны 1 =633 нм, фокусное расстояние f =4 % =2,53 мкм. Размер расчётной области: [-8 1 ,8 1 ] X [-8 1 ,8 1 ] X [0,8 1 ]. Шаг дискретизации по всем координатам 1 /16. Время моделирования 20 периодов (т.е. 20 1 / е , где е -скорость света в вакууме). Шаг дискретизации по времени 1 /32.

На рис. 6 видно, что происходит фокусировка в пятно. Это пятно имеет форму эллипса с минимальным диаметром по полуспаду интенсивности примерно 0,65 1 .

Кроме фокусного пятна, формируется светлое кольцо (боковой лепесток) с максимальной интенсивностью, составляющей 2,5% от максимальной интенсивности в фокусном пятне, что намного меньше, чем, например, в моде Бесселя нулевого порядка, для которой интенсивность первого кольца составляет 16% от интенсивности в центре дифракционной картины.

Фокусировки в продольную осевую линию r =0 ( z >  f ), как это может показаться из (35), не происхо-

6-

4-

2-

0^J---г б)

-4

8 х/Х

Рис. 6. Моделирование FDTD-методом фокусировки пучка Ханкеля-Бесселя (n = 0, f = 4 1 ): модуль амплитуды E x в момент времени t = 20 1 /е (а) и интенсивность I = |E_x|² + |E_y|² + |E_z|² (б) в плоскости Oxz

^Еп = 0 ( ^r<< ^{z - f} , Ф , ^z ) = i n E 0 H 0 ¹ ’

r ^{2 +}( z ^- f ) ^{2 -} f ⁺ z

—E ₀ In

kr ²

4 (z - f)

kr ²

4 (z - f)

~

X

' r2 +(z - f )2 - f + z| .

При r =0 логарифм принимает бесконечные значения для любых z , но при любых других r , близких к нулю, логарифм убывает с ростом z . Поэтому при моделировании получилось, что после фокусной точки z = f интенсивность убывает вдоль оптической оси.

Аналогично было промоделировано распространение поля с вихрем n =3. Модуль амплитуды E x в плоскости Oxz показан на рис. 7. Параметры моделирования те же. Здесь также не происходит продольного смещения фокуса, и самое узкое место пучка расположено в плоскости z = f . Интенсивность в поперечной плоскости и её сечения показаны на рис. 8.

Из рис. 2 может показаться, что можно добиться сколь угодно узкого провала интенсивности в центре дифракционной картины. Однако в этом случае потребовалось бы использование начального поля (36) бесконечной ширины.

На практике это невозможно, и поэтому FDTD-методом была получена картина, показанная на рис. 8.

• 7                    И

• Толщина кольца по полуспаду интенсивности примерно равна длине волны.

z/X h

• -8      -4      0      4      8 x/X

Рис. 7. Моделирование FDTD-методом фокусировки пучка Ханкеля-Бесселя (n = 3, f = 4 λ ): модуль амплитуды E_x в момент времени t = 20 λ /c

а)-8-4   0   4    8

Рис. 8. Распределение интенсивности в плоскости z = f: двумерная картина (а) и её вертикальное (б) и горизонтальное (в) сечения

Заключение

В данной работе было получено точное решение скалярного уравнения Гельмгольца, описывающее световой пучок, распространяющийся в положительном направлении вдоль оптической оси. Комплексная амплитуда такого пучка пропорциональна произведению двух линейно независимых решений уравнения Куммера. Получены выражения для частного случая таких пучков – пучков Ханкеля-Бесселя. Исследована фокусировка пучков Ханкеля-Бесселя.

Работа выполнена при поддержке ФЦП «Научные и научно-педагогические кадры инновационной России» (госконтракт № 14.740.11.0016), грантов Президента РФ поддержки ведущих научных школ (НШ-7414.2010.9) и молодого кандидата наук (МК-64571.2010.2).