Лазерные пучки Эйри с гиперболической траекторией в ближней зоне

1. Пучки Эйри с параболической траекторией

В 1974 году Kalnins и Miller [1] нашли решение параксиального уравнения распространения в виде функций Эйри. В 1979 году Berry и Balazs [2] рассмотрели неуширяющиеся волновые пакеты в квантовой механике. В 1994 году Besieris и др. [3] нашли решение 2D параксиального уравнения

(     ^ ²       ^1

U ( s , ^ ) — Ai I s —4 + ia ^ IX

(is^ ia2^ i ^3 a ^2     )Xexp — + — ---— + as ,

I 2     2 12 2 I

d U d ² U d ² U _n

2 i --+ —. I— = o 0

'-   d sx   d s2

который в начальной плоскости при ξ =0 даёт функцию Эйри с экспоненциальной аподизацией

U ( s , ^ — 0 ) — Ai ( s ) exp ( as ) , a >  0,            (7)

в виде

(     £2 I (

^U ( ^Sx , S y , ^ ) = Ai I s ^- —I ^A 1 I S y

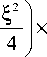
( S^ iSy ^ X exp —— + ——

I 2      2

-

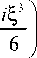
где a – постоянная. В [4] также показано, что сформировать 1D пучок ПЭ с конечной энергией можно при освещении гауссовым пучком фазовой маски с кубической зависимостью от поперечной координаты и выполнением преобразования Фурье с помощью сферической линзы. Это следует из того, что Фурье-образ начального поля (7) имеет вид:

где Ai( x ) – функция Эйри, равная при вещественных положительных значениях аргумента

2 it 2 a

F ( t ) — exp ( - at ) exp I — - ia t + — I .

Ai ( x ) = п 1 ( x] 3 ) 12 K ₁₃ ( 2 x 3²/ 3 ) = = V x [ I - 13 ( 2 x ³²/3 ) - 1 13 ( 2 x 3 ²/3 ) ] /3,

I 1/3 ( x ) и K 1/3 ( x ) – модифицированные функции Бесселя первого и второго родов, s x = x / x 0 , s y = y / x 0 , ξ = z /( kx 0² ) – безразмерные поперечные и продольная декартовы координаты, k = 2п/ % - волновое число , x 0 – произвольный поперечный размер. Пучки Эйри (ПЭ) в [1 –3] имеют бесконечную энергию, так как функция Эйри медленно убывает при x → ∞:

Ai ( - x ) = п ¹² x A⁴ sin [ ( 2/3 ) x ^3/2 + (л/ 4 ) ] . (4)

В 2007 году Siviloglou и Christodoulides [4] рассмотрели ПЭ в оптике с конечной энергией. Они показали, что решение уравнения (1) в 1D варианте

Главной особенностью ПЭ является изогнутость траектории главного максимума (основного лепестка). Он распространяется по параболической траектории. Поэтому ПЭ называются ускоряющимися или баллистическими (так как свободно падающее тело двигается по параболе с ускорением g ). Однако в [5] показано, что для ПЭ с конечной энергией (6), (7) «центр тяжести пучка» не смещается при распространении и ускоряющий эффект проявляется только при малых значениях параметра a << 1. В [6] экспериментально, с помощью жидкокристаллического модулятора света, была получена параболическая траектория распространения 1D ПЭ, которая хорошо описывалась формулой ( a = 0,1):

_ dU d 2U__ 2 i--1--— — 0

d^ ds2

I    ^z I x  ( 4nx032 J ,

имеет вид

где ( x, z ) – поперечная и продольная декартовы координаты. В [7] получено обобщение ПЭ – пучки

Эйри–Гаусса (ЭГ) и рассчитано их преобразование в оптической ABCD-системе. Если ПЭ с бесконечной энергией в начальной плоскости в [1, 2] имеют вид E ₀( x , z =0) = Ai( x ), а пучки с конечной энергией из [4] имеют в начальной плоскости вид (7): E 0 ( x , z =0) = Ai( x ) exp ( ax ), то ЭГ-пучки из [7] в начальной плоскости имеют следующий вид:

где σ – радиус гауссова пучка. В [12] Bandres рассмотрел ещё один тип ПЭ – ускоряющиеся пучки. Он нашёл решение уравнения

d д ² д ²

' эТд7 ■. I E ⁽ u , ^v , ^{а= 0}

E2 (x, z = 0) = Ai I x^" IX

X exp

( a + ib ) x - x - + ikx— , w 2   2 R

в виде

E5 (u, v, £) = Ai (u + to2 ) XXexp Гi^(u - %-^2) + i^3/31exp(itov),

где δ , β , a, b, w, R – параметры. В [8] показано, что добавка к ПЭ [1] линейного наклона позволяет управлять параметрами параболической траектории. Получено выражение для преобразования Френеля от ПЭ в начальной плоскости вида

E 3 ( 5 , z = 0 ) = Ai ( 5 ) exp ( as + i v s ) , s = x/x ₀, (11)

где λ , ω – константы. Хотя этот пучок двумерный, но по одной координате его траектория параболическая, как у 1D ПЭ. В [13] численно показано в непараксиальном случае, что 2D поле с кубической фазой, ограниченной круглой диафрагмой с радиусом R

E_x ( x , y , z = 0 ) = circl

( I 2 , 2" У ^{x +} y

V

R

J

X

и показано, что траектория такого пучка, в отличие от (9), имеет вид

X exp Г i p ( x ³ + y ³ )

vz

x =--+ kx0

z ²

4 k ² x ₀³ .

В [9] численно рассчитаны вектор Пойнтинга и орбитальный угловой момент для ПЭ. В [10] Ban-dres рассмотрел ускоряющиеся параболические пучки. В начальной плоскости их комплексная ампли-

туда имеет вид:

E4 (u,v,z = 0) = 0n (n)0n (iS)X

X exp [ iw ( n ² -^ ² ) /2 + i ^ 3/3 ^ , где ξ и η – параболические координаты:

u -%- w ² = ( n ² -^ ² ) /2,

_ v = n^,

а функции θ _n ( x ) удовлетворяют уравнению ангармонического осциллятора:

также имеет параболическую траекторию до и после Фурье-плоскости. В [14] с помощью трёхволнового смешения в нелинейном фотонном кристалле и с помощью управления температурой получили два режима (генерацию второй гармоники и генерацию разностной частоты), в которых начальный кубический волновой фронт генерировал ПЭ с параболами, направленными в разные стороны. Аналогично [13], в [15] численно исследуются 1D ПЭ, ограниченные по поперечной координате, и линейная комбинация ПЭ, которая при распространении формирует две параболы, направленные в разные стороны, аналогично [14]. В [16] исследуется влияние взаимного смещения центра гауссова пучка и центра кубической фазовой маски на формирование модернизированных ПЭ в Фурье-плоскости. Получено явное выражение для Фурье-преобразования от начальной функции

[- 2 ^^T + y J 0 n (n) = E0 n (П).            (15)

E ₆ ( t ) = exp ^|- a ( t ^- t 0 ) 2 1^X

X exp ^ i

Для функции θ n ( x ) не известно аналитического решения в виде специальных функций, известна только асимптотика:

⁰ n ( i s ) = sin ( v2 ^7 ^{6 +п} 6 )Д , ^^ .       ⁽¹⁶⁾

В [11] экспериментально с помощью 35 фс импульса на средней длине волны % = 0,8 мкм с энергией 10 мДж в воздухе из-за многофотонной ионизации получен искривлённый плазменный канал радиусом около о =132 мкм и длиной 69 см, который хорошо описывается формулой:

x = 0,037 %у-, о ³

⁽ t ^- t 1 ) 3

-

2( a .a a (t-t1)--у i

Показано, что выбором постоянных t 0 и t 1 можно управлять видом параболической траектории ПЭ. В [17] изучается другой тип ограниченных с одной стороны по поперечной координате 1D ПЭ с конечной энергией. В начальной плоскости эти ПЭ имеют следующую комплексную амплитуду:

E 7 ( s , ^ = 0 ) = Ai 0 ( s ) ± i Bi 1 ( s ) ,

где Ai( x ) и Bi( x ) – два линейно независимых решения уравнения Эйри

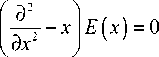
но ограниченных с одной стороны специальным образом:

. _ | Ai( 5 )exp( asA , s <  s,, =- 2,3381,

Ai ( s ) = J ⁽ ) ^P( ) ,       ⁰       ,       ,      (24)

[ 0, s >  s 0 ,

, _   |Bi( s )exp( as ), s < s, =- 1,1737,

Bi 1 ( s ) = J ⁽ ) ^P( ) ,        ¹       ,       ,       (25)

[ 0, s >  s 1 .

Распространение таких модернизированных ПЭ исследуется в [17] численно. В [18] предложен радиально-симметричный ПЭ c конечной энергией, который «самофокусируется» на определённом расстоянии:

E 8 ( r ) = ^Ai ( r ^- r 0 ) exp [ a ( r ^{- r} 0 ) ] ,                ⁽²⁶⁾

где r и r ₀ – переменная и постоянная поперечные радиальные координаты. Фокусное расстояние зависит от величины r 0 . Распространение пучка моделируется численно. В [19] теоретически показано, что с помощью тонкого клинообразного кристалла, толщина которого меняется по поперечной координате линейно, и при накачке гауссовым пучком вблизи выходной поверхности кристалла возникает обрезанный ПЭ с ускорением (с параболической траекторией движения). B [20] численно и экспериментально рассматривается ПЭ, названный «световой пулей». В начальной плоскости в любой момент времени его комплексная амплитуда имеет вид:

E9 (x, y, z, t ) = f       в Z 2

= Ai ( ^xl^x 0 ) Ai ( y/ y 0 ) Ai l V^T 0 ^-

I        ^{4 t} 0

где τ = t – z/c , x 0 ; y 0 , τ 0 и β – постоянные.

2. Пучки, ускоряющиеся по непараболической траектории

В [21] методом стационарной фазы из интеграла Френеля получено выражение для комплексной амплитуды поля, которое фокусируется на кривой x = f ( z ):

показателя преломления и удовлетворяющее параксиальному уравнению в безразмерных единицах (подобному уравнению (1)):

f i + 1

^ d z 2 d x²

a ( z ) x )          _n

------ E ( x , z ) = 0

2 J

где α( z ) – функция от продольной переменной z . Получено решение уравнения (29) в виде интегралов для любой α( z ) и при начальном поле вида E ₀( x , z = 0) = Ai(Y 1^/3 x ), где Y — масштабирующий множитель. В [23] получено уравнение для фазы φ( x ) светового поля, которое направляет лучи на 1D каустическую кривую c ( z ):

d ^ ( x )       k [ c ( z ) - x ]

d x     V[ c ( z ) - x ]² + z ² ,

где k – волновое число света. Из этого уравнения следует, что при c ( z ) = az ² фаза получается в степени 3/2, а сама амплитуда ПЭ в начальной плоскости имеет вид:

E 11 ( x , z = 0) = exp ( - i 4 4akx ^3/2/3 ) ,             (31)

где a – постоянная. Если уравнение каустики имеет вид c ( z ) = az ⁴ , то начальное поле будет иметь следующий вид:

E ₁₂( x , z = 0) = exp ( - i 16(3 a )^1/3 kx ^7/4 / 21 ) .        (32)

Аналогично в [23] найдена явная фаза для каустики c ( z ) = az ^т , где m – целое число.

В [24] теоретически и экспериментально изучалось ускорение ПЭ с помощью градиентной оптики. Для параксиального уравнения со слабым линейным показателем преломления:

. d

* d z

1 d ²

2 k d x ²

-

k ⁵ x К

—— I ^{E ( x} , ^z ) = ⁰

2 n J

где 5 • x <<  n , n - показатель преломления среды, получено явное решение в виде:

E ₁₃ ( x , z ) = Ai

^

E10 ( x, z ) = E Cn Ai n=1

k ^2/3 ( ф" ( x 0 n ) ^{+ 1} Z )

1 f z ²       5 z ² 1 . az

— l x--2—3---I + i— x 0 (    4 k x 0   2 n J   kx 0

4/3

2 2“ (ф" ( x 0 . ) )

x exp

ax

-

az ²

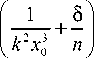
где φ, φ ′′ , φ′′′ – фазовая функция поля в начальной плоскости z = 0 и её вторая и третья производные, x 0 n – стационарные точки показателя экспоненты в интеграле Френеля, равного k φ + k ( x – x ₀) ² /(2 z ), где x ₀ – координата в начальной плоскости. Эти стационарные точки удовлетворяют условию x = x 0 n + z φ′( x 0 n ). С помощью формулы (28) и пространственного модулятора света экспериментально получены ПЭ, траектории которых описываются полиномом x = z^m , где m = 1,5; 2; 3; 4; 5. В [22] рассмотрено световое поле, распространяющееся в планарной градиентной неоднородной среде с линейным распределением

x exp

iz3 f 1     2k52 35 1 ia2z l +1I +

12 ^ k ³ x 0 n ²     nkx 0 J    2 k

x exp ixz

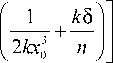
удовлетворяющее граничному условию:

E ( x , z =0) =Ai ( x / x 0 ) exp ( ax ), a >0.

В [25] экспериментально получены плазмонные ПЭ с помощью матрицы субволновых отверстий в плёнке серебра, периодических вдоль оси z и непериодических (аппроксимирующих фазу степени 3/2) вдоль

оси x . Падающая на отверстия плазмонная волна распространяется вдоль оси x , а ПЭ распространяется вдоль оси z . В [26] c помощью жидкокристаллического модулятора, пропускание которого описывается фазовой функцией степени 3/2: ф ( x ) = ax ³2 был сформирован ПЭ. В [27] рассмотрен 2D тройной ПЭ в начальной плоскости в виде:

I r - r 1        r - r

-----1 exp a----- w ) w

x

E 14 ( x , y , z = 0 ) = Ai ( by + c ) x

..V xVs -y        -xVs -y x Ai b------ + c Ai b-------

I 2 J I 2

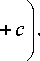
x[r exp (iф)- roexp (iф0)]n, где n – топологический заряд вихря. Этот пучок формирует в фокусе световое кольцо. В [33] методом виртуального источника найдены непараксиальные поправки к параксиальным ПЭ. В [34] исходя из 2D пучка Матье, взяв его одномерное сечение, рассмотрены ускоряющиеся по эллиптическим орбитам лазерные пучки. Пучок Матье выбирается в виде:

Этот пучок имеет конечную энергию. Фурье-образ этого пучка в [27] найден аналитически, а преобразование Френеля рассчитывается численно. В [28] во внешнем резонаторе ND:YAG лазера в качестве зеркала использована отражающая дифракционная решётка с рельефом:

E 17 ( u , v , z = 0 ) =

= Ace m ( ^v ) Mc m ( u ) ⁺ iBse m ( ^V ) ^M s m ( u ) ^,

T ⁽ x ^, y ) = \

I     | 2 n x x ³    y ³

sgn <  cos l-- 1---1--

I    l %      a    a

+ 1 , (36)

где h 0 – высота зубьев решётки, a – масштабирующий множитель. В этом случае лазер генерирует 2D ПЭ. В [29] в интегральной форме для функции Бесселя предложено интегрировать только по половине круга от нуля до π:

К

J + ( x , z ) = J exp [ i V t + ik ( x cos t + z sin t ) ] dt . (37) 0

Формула (37) описывает 1D ускоряющийся пучок, распространяющийся по круговой траектории с поворотом почти на 90 градусов. В [30] рассмотрен 2D пучок Бесселя, но интерпретирован он как 1D пучок, распространяющийся вдоль оси z :

где A, B – постоянные, ( u , v ) – эллиптические координаты x = f ch( u ) cos( v ) , y = f sh( u ) sin( v ), ce, se – угловые и Mc, Ms – радиальные функции Матье. Для ускоряющегося пучка надо положить v =0 (или v = π/2).

В приведённом выше подробном обзоре работ по ускоряющимся пучкам, и в частности ПЭ, нет работ по ПЭ, которые ускоряются по гиперболическим траекториям. Чтобы заполнить этот пробел, рассмотрим далее пучки Эйри второго рода (ПЭ-2) или гиперболические ПЭ.

E 15 ( x , z ) = J _v ( k^x ² + z ² ) exp l i V arctg —

3. Лазерные пучки Эйри второго рода

Обычно 1D ПЭ формируют с помощью начального поля (8) – фазовой кубической маски, далее формируют с помощью сферической линзы Фурье-спектр поля (8), который описывается функцией (7). А за Фурье-плоскостью формируется ПЭ с комплексной амплитудой (6). ПЭ-2 возникают в зоне Френеля фазовой маски (8). Чтобы показать это, рассмотрим комплексную амплитуду гауссова пучка сразу за кубической фазовой маской:

где J ν ( x ) – функция Бесселя. Причём при z =0 выбирается только на полуоси:

E ⁺ ( x , z = 0 ) = J p ( kx + P ) exp ( - ax ) 6 ( x + Р/ k ), (39)

E ( x ,0 ) = exp

x ²

—r + i a w ²

x 1

x ₀

■о I x + i в l — l x0

где θ( x ) – функция Хэвисайда. Ускоряющийся пучок (39), как и пучок (37), поворачивается при распространении по окружности на 90 градусов. В [31] экспериментально с помощью модулятора и лазерного импульса длительностью 10 фс получен световой пучок с кривой каустикой в виде окружности с радиусом 35 мкм. При этом на жидкокристаллическом модуляторе формировалась фазовая функция, рассчитанная с помощью уравнения геометрической оптики, аналогичного уравнению (30):

где w - радиус перетяжки гауссова пучка, a и в -безразмерные параметры фазовой маски. Тогда на расстоянии z от начальной плоскости в параксиальном приближении амплитуда светового поля будет описываться преобразованием Френеля:

+^

E

x exp

t ² . t t

—7 + i a l — w     l x ₀

ik ,        \2

ехр 2- ( x ^- t )

-и

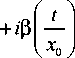
d t .

x

dф( x) =    kc'       ‘ = dc dx     1 + (cУ ’      dz

Дополняя показатель экспоненты до полного куба и используя известное интегральное представление для функции Эйри

В (40) функция c ( x ) задаёт нужную каустическую кривую, например, дугу окружности.

В [32] рассмотрен круговой ПЭ с оптическим вихрем с начальной амплитудой:

x 1 7      fit3

Ai ( x ) = — [ exp-- + ixt d t ,

V ’ 2n J

-7    x/

можно вычислить интеграл в (44). Тогда получим:

— i 2 n I k

E ( x , z ) = . ------ wp x

z

ikx ²      , v 2, 6

^x exp "2Г⁺ sp ( qp ) ⁺ 3( qp ) ⁺ ikz ^x

значению, в котором функция Эйри имеет локальные максимумы y_m :

kx ₀ x    k ² x ₀ ⁴

z    12 a z ¹

= У т .                  (50)

x Ai [ sp + (qp )4 ], где kw2           iz z 0 = —, q =1 —,

2 z

Числа y m в (50) принимают следующие значения:

w ( „ kx„x I

s = — I p--— I, p x 0 I     z )

x ₀ .

w V3 a

В исходных обозначениях из (43) вместо (46) можно записать:

E ( x , z ) =

— i 2n k x_n

--;= x z 3j 3a

x exp

f x

3a ( w )

p _— ^kx 0 ^x

z

+--7 27a2

^x 0 )

w

1 — 3 z' z

x

x exp

ikx ²

2 z

i ^z 0 ¹ I ^x 0 | z 3 a ( w )

в_— kx 0 ^x

z

x

x exp

x Ai

2 i

^x 0 I

27 a ² ( w

3 A

3 z — z r + ikz x z    z ³ J

kx_nx 1 f x_n 1

P+ I Iz 3a I w )

1 — iz^ I z )

.

Выражение (48) описывает ПЭ-2 с конечной энергией. Из (48) видно, что ПЭ-2, в отличие от ПЭ (6), имеет квадратичную, а не линейную фазу, и поэтому при распространении он будет расходиться. Кроме того, в (48) аргумент функции Эйри комплексный, как и в (6), но зависимость от координаты z имеет другой характер: в (6) значение аргумента функции Эйри пропорционально z ² , а в (48) – обратно пропорционально z . ПЭ-2 с бесконечной энергией можно получить, если вместо гауссова пучка осветить кубическую фазовую маску плоской волной ( w → ∞). Тогда вместо (48) получим выражение:

.     — i2 n k x₀

E ( x , z ) = .-- p0= x

V z ^/3a

x exp

x Ai

ik

2 z

x 2 + kx 0 ^x _— P ^x 0 1 k ^x 0

3 a z   3 a   54 a ² z ¹

+ ikz x (49)

1 f _R kx ₀ x   k ² x ⁴ ।

( 3 a ) ¹³ 1^в        " 12 a z ² )

Выражение (49) описывает ПЭ-2 с бесконечной энергией. Но квадратичная зависимость фазы сохраняется, и поэтому пучок (49) будет при распространении расходиться. Аргумент функции Эйри в (49) действительный. Приравняем этот аргумент к

Таблица 1

m	y m
0	–1,01879
1	–3,2482
2	–4,8201
3	–6,16331
4	–7,37218
5	–8,48849
6	–9,53545
7	–10,5277
8	–11,4751
9	–12,3848
10	–13,2622

Из уравнения (50) можно найти явное уравнение траектории максимума ПЭ-2:

^x = kx 0 ( ^p— y- ^

kx ₀ ³

12 a z

В отличие от параболической траектории (9), по которой распространяются ПЭ, ПЭ-2 распространяются по гиперболической траектории.

Найдём производные по z от выражения (51):

d x d z

= kx ;^(P— y - 3^{: a} - '

d² x       kx ₀ ³

d z ²     6 a z ³

kx ₀ ³

12 a z ² ,

Гиперболическая траектория (51) обладает ускорением на тех участках, на которых производные первого и второго порядка (52) и (53) имеют один знак. Отсюда следует, что для ускорения траектории должно быть

1 12 a

2 <  ;24

z k x ₀

(У- V3a —P)

причём условие для ускорения не зависит от знака x ₀/ a . Для существования расстояний z , удовлетворяющих (54), правая часть этих выражений должна быть положительной. Это возможно, когда a >0 и P < y m (3 a ) ¹/³ либо a <0 и P > y m (3 a ) ¹/³ , т.е.

sign ( ^a ) ^p< у - ^Зр .

Если условие (55) выполняется, то ускорение наблюдается на расстояниях

z >  z 1

kx ₀ ^{2 ,} 2^3 a ( у - V3 a — ^p )

причём в отличие от пучков Эйри первого типа ускорение не постоянное, а убывающее пропорционально z ^–3 , начиная со значения

d² x

z = Z 1

= <

' 473а/ _3RV^/2       a

—      ( Ут 3/3а~в] , а> 0, kx

“                                 (57)

^72-1^ (в — Ут V3^а< 0.

k x ₀^x '

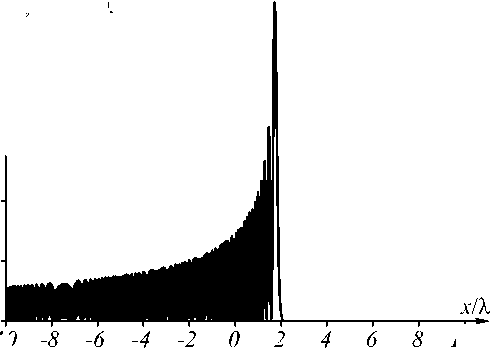
Рассмотрим для примера следующие значения параметров: X = 532 нм, x 0 = X , а =-1, в =10, т = 0, y ₀=–1,01879. В этом случае условие (55) выполняется и траектория обладает ускорением при z >  z ₁ ≈ 330 нм. График траектории при указанных параметрах изображён на рис. 1 а , а распределение интенсивности поля (49) при этих же параметрах – на рис. 1 б . Рас-

,. I, отн. ед.

1,00"

0,80-

0,60-

0,40

0,20

а)

I, отн. ед.

0,60-

чётная область на рис. 1 б имеет размеры 10 X< x < +10 X , 0 < z < 4 X .

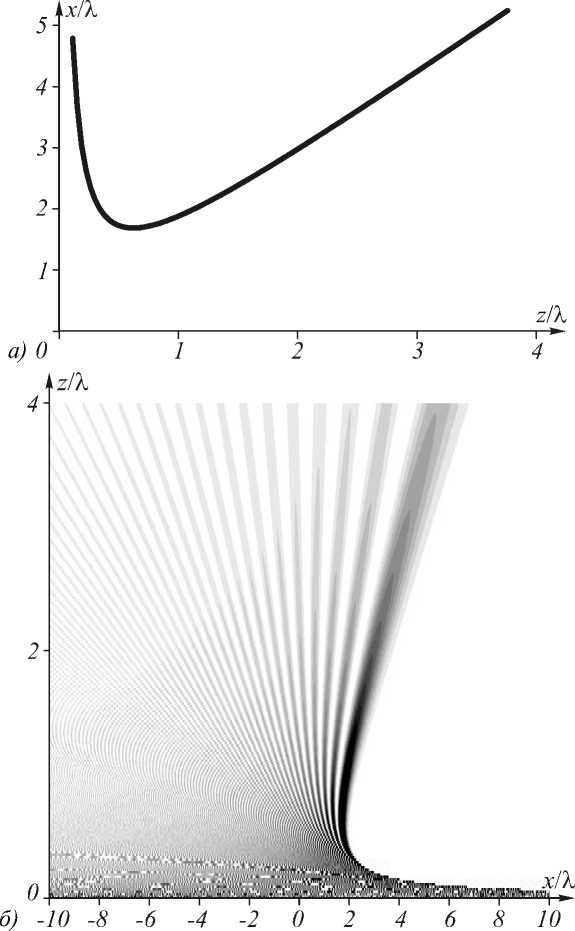
Рис. 1. Траектория ПЭ-2 с ускорением (а) и распределение интенсивности ПЭ-2 с ускорением в плоскости xz (б)

На рис. 2 показаны сечения интенсивности в плоскостях z = X /2 ( а ), X ( б) , 2 X ( в ), 3 X ( г ), 4 X ( д ).

Для сравнения рассмотрим пучок Эйри первого типа (6) при a =0. Приравняем в (6) аргумент функции Эйри к значению, в котором она имеет локальные максимумы y_m , и найдём явное уравнение траектории максимума ПЭ:

–

б)

0,45-

0,30-

0,15

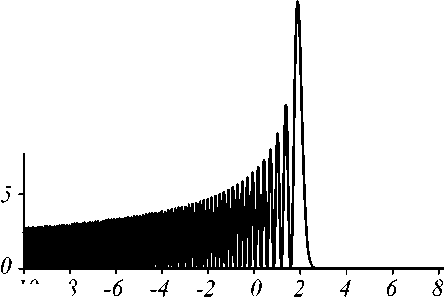
xfk

-10 -8

I, отн. ед.

0,30^

0,20-

’”|в1вИ

2 z

x!X

О

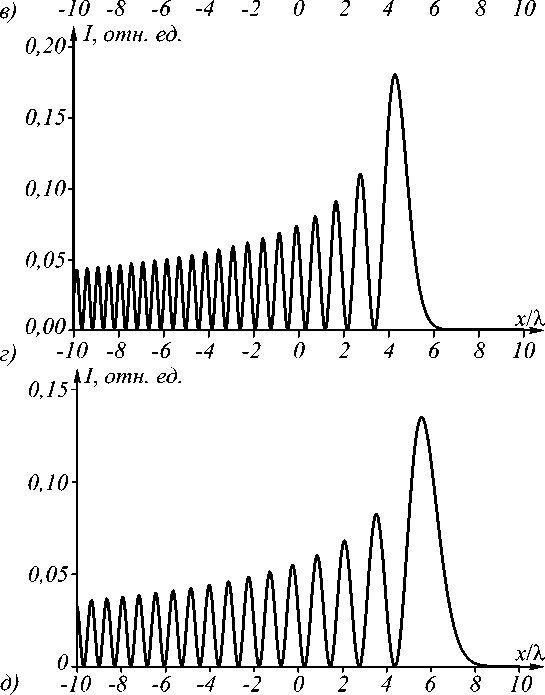
Рис. 2. Сечения интенсивности пучка ПЭ-2 в плоскостях z = X/2 (а), X (б), 2X (в), 3X (г), 4X (д)

Из (58) видно, что пучок ПЭ обладает постоянным ускорением, равным 1/(2 k ² x ₀ ³ ). Из (58) также видно, что ПЭ (6) – нерасходящийся (бездифракционный), так как x ₁ – x ₂= x ₀( y_m – y_n ) не зависит от z , а для ПЭ-2 из (51) следует, что x ₁– x ₂= (3 α ) ^1/3 z ( y_m – y_n )/( kx ₀) и пучок линейно расходится с ростом z .

На рис. 3 показано распределение интенсивности поля (6) при следующих параметрах – λ =532 нм, x ₀ = λ /2. Расчётная область на рис. 3 имеет те же размеры: –10 λ ≤ x ≤ +10 λ , 0 ≤ z ≤ 4 λ . Согласно (58), ускорение для такого пучка равно 1/( π ² λ ), тогда как согласно (57) для пучка ПЭ-2, показанного на рис. 1 б , при z = z 1 ≈ 330 нм ( z 1 получено из (56)) оно равно примерно 19,87/( π ² λ ). Этим и определяется более изогнутая форма траекторий на рис. 1 б .

-JO -8 -6 -4 -2   0 2   4   6   8 10

Рис. 3. Распределение интенсивности ПЭ-1 (с постоянным ускорением) в плоскости xz

Заключение

В работе получены следующие результаты:

– приведён достаточно подробный обзор научных работ по ускоряющимся лазерным пучкам, в том числе и пучкам Эйри; обзор сделан с целью доказать, что световые пучки, порождённые кубической фазовой маской в зоне Френеля, до сих пор рассмотрены не были;

– получен явный вид комплексной амплитуды, описывающий дифракцию Френеля гауссова пучка на фазовой маске с кубической зависимостью фазы от поперечной координаты (уравнение (48));

– рассмотрены одномерные пучки Эйри второго рода с конечной энергией (уравнение (48)) и с бесконечной энергией (уравнение (49)), которые распространяются с ускорением на участке гиперболической траектории (уравнение (51));

– показано, что пучки Эйри второго рода имеют неоднородное «ускорение», которое быстро затухает (пропорционально кубу расстояния), и пучок продолжает распространяться по прямолинейной траектории (рис. 1);

– показано также, что пучки Эйри второго рода в ближней зоне (несколько длин волн от кубической фазовой маски) имеют «ускорение» на порядок большее (при прочих равных параметрах), чем обычные пучки Эйри, распространяющиеся по параболической траектории;

– пучки Эйри второго рода с бесконечной энергией при распространении расходятся (центральный максимум интенсивности уширяется) линейно с расстоянием от начальной плоскости.

Работа выполнена при поддержке ФЦП «Научные и научно-педагогические кадры инновационной России» (соглашение № 8027), грантов Президента РФ поддержки ведущих научных школ (НШ-4128.2012.9), молодого кандидата наук (МК-3912.2012.2) и молодого доктора наук (МД-1929.2013.2), а также грантов РФФИ (12-07-00269, 12-07-31117, 13-07-97008).