Learning a Backpropagation Neural Network With Error Function Based on Bhattacharyya Distance for Face Recognition

Published Online August 2012 in MECS

Face recognition can be defined as the ability of a system to classify or describe a human face. The motivation for such system is to enable computers to do things like human do it so to apply computers to solve problems that involve analysis and classification. Research in this area has been conducted for more than 30 years; as a result, the current status of the face recognition technology is well advanced. Face recognition has received this great deal of attention because of its applications in various domains like Security, identity verification, video surveillance, Criminal justice systems and forensic, Multi-media environments [12].

Many research area affect the field of face recognition: pattern recognition, computer vision, neural networks, machine learning, etc…

Neural networks have been widely used for applications related to face recognition. One of the first neural networks techniques used for face recognition is a single layer adaptive network called WISARD [13]. Many different methods based on neural network have been proposed since then and the major of them use neural networks for classification. In [16] Radial Basis neural network was used to detect frontal views of faces, curvelet transform and Linear Discriminant Analysis(LDA) were used to extract features from facial images, and radial basis function network(RBFN) was used to classify the facial images based on features taken from ORL database. In [14] the focus was to investigate the dimensionality reduction offered by random projection (RP) and perform a face recognition system using back propagation neural network. Experiments show that projecting the data onto a random lower-dimensional subspace yields results and give an acceptable face recognition rate. Bhattacharjee et al. developed in 2009 a face recognition system using a fuzzy multilayer perceptron using back propagation [15].

The way in constructing the neural network structure is crucial for successful recognition. In general, neural networks are trained to minimize a squared output error which is equivalent to minimizing the Euclidian norm of the difference between the target and prediction vectors. The major limitations of this algorithm are the existence of temporary, local minima resulting from the saturation behavior of the activation function, and the slow rates of convergence .many researchers have be done to overcome these problems. In this context, a number of approaches have been implemented to improve the convergence speed. There are basically on selection of dynamic variation of learning rate and momentum, selection of better activation function and better cost function. Some related researches are presented in [3].

Until recent years gray-scaled images were used to reduce processing cost [4][5]. Nowadays, it is demonstrated that colour information makes contribution and enhances robustness in face recognition [6].

Our aim in this paper is to introduce the use of color information with minimal processing cost using the Back Propagation algorithm, and to accelerate the training procedure we use Bhattacharyya distance instead of the traditional mean square error(MSE) based on the Euclidian distance to seeks the global minima on the error surface.

The remainder of the paper is organized as follows:

Section (2) gives an overview about the back propagation neural network. Section (3) presents the Bhattacharyya distance for similarity measurement. In section (4), we present our proposal solution for face recognition. Section (5) gives the experimental results. Finally, Section (6) gives a conclusion.

• II.  The Back propagation neural network

Back propagation is a multi-layer feed forward, supervised learning network. The network represents a chain of function compositions which transform an input to an output vector. It looks to minimize the error function using the method of gradient descent. The learning problem consists of finding the optimal combination of weights so that the network function approximates a given function as closely as possible. In other word, gradient descent is used to update weights to minimize the squared error between the network output values and the target output values; The update rules are derived by taking the partial derivative of the error function with respect to the weights to determine each weight’s contribution to the error. Then, each weight is adjusted, using gradient descent, according to its contribution to the error. This process occurs iteratively for each layer of the network, starting with the last set of weights, and working back towards the input layer, hence the name back propagation. The aim is to train the network to perform its ability to respond correctly to the input patterns that are used for training and to provide good generalization ability to input that are similar.

Traditionally, Back propagation adjusts weights of the NN in order to minimize the network total mean squared error. E indicating the total error on all of the training data, it is defined as:

E = E 1 + E 2 + ... + E m                              (1)

Where E i is the mean squared error (MSE) of the network on the i ^th training example, computed as follows:

Ei= ∑ (Desiredi– Actuali)2                        (2)

In statistics, the mean squared error or MSE of an estimator is the expected value of the square of the ‘error’. The error is the amount by which the estimator differs from the quantity to be estimated.

The Convergence value is the threshold value that is used in the training process. When the sum of the total error for all training data in the model is below this value, the training process is completed.

Summarizing, the learning process step is as follow:

Read data and specify the desired output for each vector.

Randomly initialize weights and bias.

Then gradually adjust the weights of the network by performing the following procedure for all patterns:

Compute the hidden layer and output layer neuron activation:

Calculate errors of the output layer and adjust weights.

Wji(n) = шДп -1) + ^(n^n) + a^w^n - 1)

With:

’ е,(п)у,(п)|1-у,(п)]          If j Є output layer

^(njll-y^n^d^n)^^) 1 я '

layer

η and α are learning rate and momentum factor (0<η,α<1).

These steps are repeated on all patterns until minimizing the error function.

The error calculations used to train a neural network is very important. Quantifying the output error provides a way for iteratively updating the network weights in order to minimize that error. It is therefore important for success the application, to train the network with a cost function that resembles the objective of the problem at hand; Falas and Stafilopatis present in [7] results of a comparative study on the impact of various error functions in multilayer feed forward neural networks used for classification problems.

• III.    bhattacharyya measure

The original interpretation of the Bhattacharyya measure was geometric. Two multinomial population each consisting of k classes with associated probabilities p 1 , p 2 , …., p k and p’ 1 , p’ 2 , …., p’ k respectively. Then as ∑ p i =1 and ∑ p’ i =1, Bhattacharyya noted that ( √ p 1 , √ p 2 ,…., √ p k ) and ( √ p’ 1 , √ p’ 2 , …., √ p’ k) ) could be considered as de direction cosines of two vectors in k-dimentional space referred to a system of orthogonal coordinate axes. As a measure of divergence between the two populations, he used the square of the angle between the two position vectors. If θ is the angle between the vectors then:

cos(θ)= ∑ i √ (p i p i ´) (3)

Thus, if the two population are identical we have: cos(θ)= ∑p i =1 corresponding to θ=0. Then we consider the Bhattacharyya distance as adopted in similarity measurement:

Bhatt(a,b)= -ln∑ √ (ab) (4)

When a=b we obtain Bhatt(a,b)=0. Hence the intuitive motivation behind the proposed measure of similarity.

Bhattacharyya measure is a fidelity measures[8]. And it is shown in [9] that this measure is self consistent, unbiased and applicable to any distribution of data.

It was used in many application such classification. In

• [10]    authors present a feature extraction method based on the Bhattacharyya distance, the classification error was approximated using the error estimation based on the Bhattacharyya distance and find a subspace of reduced dimensionality where the classification error is minimum. They also extended the algorithm to multiclass problems by introducing the Bhattacharyya distance feature matrix. Choi et al. [ 11 ] investigate the possibility of error estimation based on the Bhattacharyya distance for multimodal data. Assuming multimodal data can be approximated as a mixture of several classes that has the Gaussian distribution, they try to find the empirical relationship between the Bhattacharyya distance and the classification error for multimodal data. Experimental results with remotely sensed data showed that there exists a strong relationship and that it is possible to predict the classification error using the Bhattacharyya distance for multimodal data.

• IV.    The Proposed Face Recognition System

There are generally two architectures adopted to design a multilayer neural network: All-Class-in-One-Network where all the classes are lumped into one super-network and One-Class-in-One-Network where a single network is dedicated to recognize one particular class. Thus, this classification problem is a two classification problem.

We adopt the use of multilayer neural network with one hidden layer and All Class in One Network architecture. Neurons in the input layer are divided into three groups, each of which is connected to a separate input vector that represents one of the three color channels. The number of neurons in the output neural network equal to the number of people to be classified: The outputs will be a vector with all elements as zero only except the one corresponding to the pattern that the sample belongs to.

We calculate the feature extractor vector of the image database using RGB components. This vector is divided into three groups, each one is connected to a separate input vector that represents one of the three color channels.

For each channel we choose an incremental rate p, so the number of sample per channel numOfSamplePerChannel becomes 256/p then we calculate the result vector for this channel:

For k=0,1,…, numOfSamplePerChannel

{ i= k*pi+p result(k) = ∑ hist(j) j=i}

This was done to create areas with homogeneous color. We obtain the extractor vector by concatenating the three result vectors.

Then, Back propagation algorithm is used to train the NN Structure proposed above. Y designs the vector of the hidden layer neurons, X the vector of input layer neurons and Z represents the output layer neurons. w is the weight matrix between the input and the hidden layer. W0 is the bias on the computed activation of the hidden layer neurons. v is the matrix of synapse connecting the hidden and the output layers, and v0 is the bias on the computed activation of the output layer neurons.

The sigmoid activation function is defined by:

f(x) =1/ (1+exp (-x))            (5)

eout and ehid are the vector of errors for each output neuron and the vector of errors for each hidden layer neuron respectively, and d is the vector of desired output.

LR and MF are respectively the learning rate and the Momentum factor.

We repeat steps 2 to 7 on all pattern pairs, The BPNN change the current weights iteratively until convergence is achieved by the minimization of the network error.

The process learning is as follow:

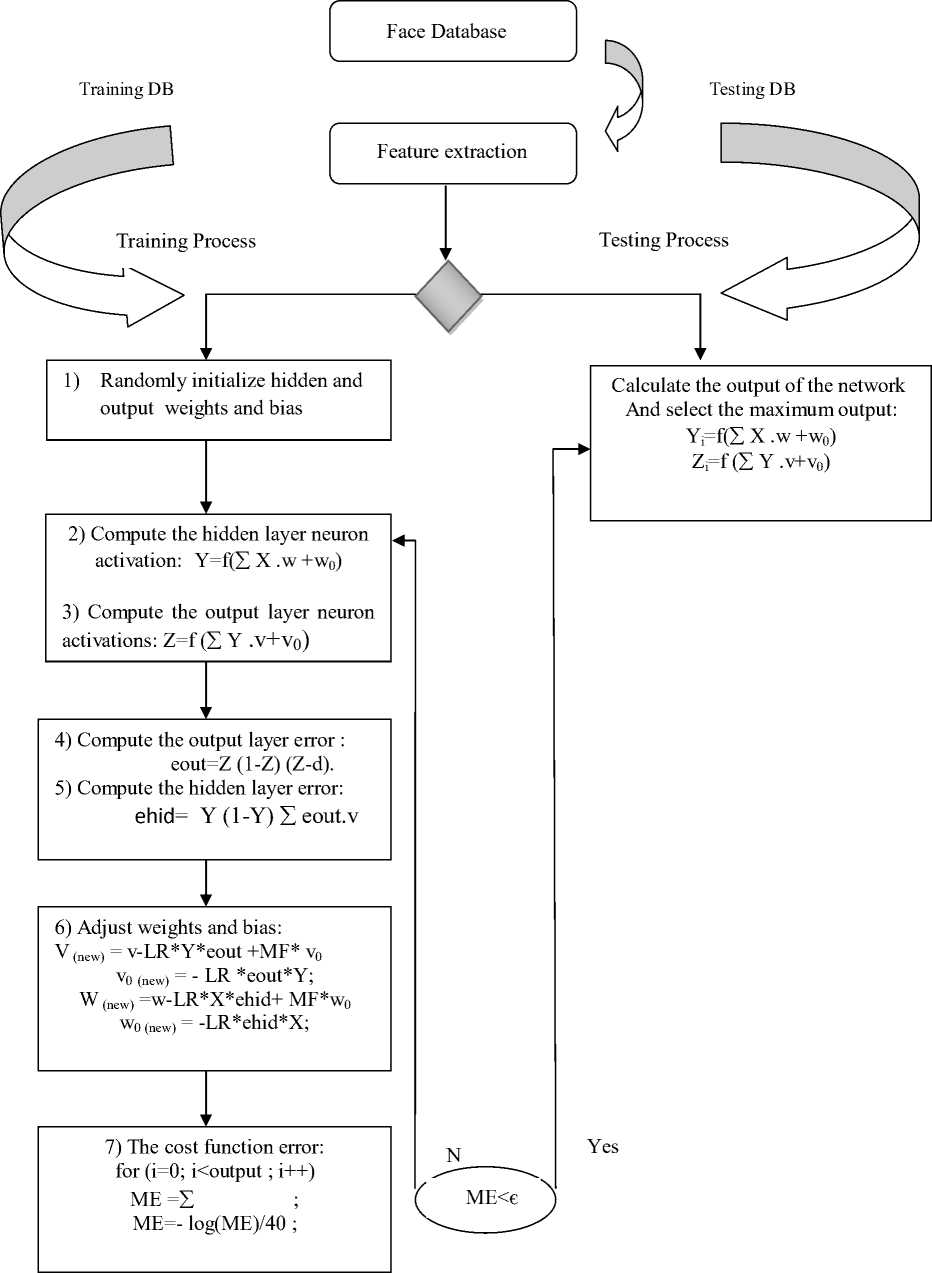
Figure.1 The architecture of the solution

• V.    Experimental results

Face image database used in our experiments is a collect of 40 Persons of Face 94, 95, grimace Directory database DB[1] and 20 Persons of Georgia DB[2]. These face images varies in facial expression and motion. Each person is represented by 20 samples in BD[1] and 15 samples in BD[2]. 5 are used for training and the rest for test.

We implement the algorithm described above with these parameters: LR=0.2; MF=0.2 and ε=0.0008. The following tables show the results of the output network using the root mean square error (RMSE) and Bhattacharyya distance respectively.

T able 1 O utput of the network using RMSE with DB[1]

Number of iteration: 1687
Neural output	The Maximum output value of Z	The desired output
Out[39]	0.9845126467014409,	39
Out[39]	0.9844009881120906,	39
Out[39]	0.9850406820289673,	39
Out[39]	0.9832801785290811,	39
Out[39]	0.9825371744421277,	39
Out[39]	0.9785333952061727,	39
Out[39]	0.9779783784960229,	39
Out[39]	0.9775947776326926,	39
Out[39]	0.983843477258687,	39
Out[39]	0.98337363013855,	39
Out[39]	0.9838527963082357,	39
Out[39]	0.9828303439608729,	39
Out[39]	0.9849472511362468,	39
Out[39]	0.9830595500118282,	39
Out[39]	0.9861510941596999,	39
Out[29]	0.7683912486716693,
Out[29]	0.4381577876197033,
Out[29]	0.45364268857695966,
Out[29]	0.5167197501158285,
Out[29]	0.5320751297873253,
Out[29]	0.45763162165016125,
Out[29]	0.3103539897565777,
Out[36]	0.4108581549363986,	impostor
Out[36]	0.6132591835927268,
Out[36]	0.7662135901900519,
Out[36]	0.8178063796785122,
Out[29]	0.6957323988073164,
Out[36]	0.6628021476715932,
Out[29]	0.678867802122425,
Out[29]	0.565031299213644,

T able 2 O utput of the network using B hattacharyya distance with DB [1]

Number of iteration: 200
Neural	The Maximum output value	The desired
output	of Z	output

Out[39]	0.9276842219492879,	39
Out[39]	0.9245430893875387,	39
Out[39]	0.9302844535559592,	39
Out[39]	0.9179548818836851,	39
Out[39]	0.9217482678874556,	39
Out[39]	0.9217999454883621,	39
Out[39]	0.92816147267565,	39
Out[39]	0.9129723688568586,	39
Out[39]	0.9197103036982968,	39
Out[39]	0.9251223448057677,	39
Out[39]	0.9253058332667181,	39
Out[39]	0.9236860173169398,	39
Out[39]	0.9265445093003952,	39
Out[39]	0.9182896351338675,	39
Out[39]	0.9328732260798309,	39
Out[29]	0.6099229153640845,
Out[11]	0.2639738638044788,
Out[11]	0.2506853845434976,
Out[11]	0.23773143711450007,
Out[11]	0.23502213721487525,
Out[11]	0.1569723251891507,
Out[29]	0.1552019594593793,
Out[36]	0.4281901063693745,
Out[36]	0.6287562960385126,	impostor
Out[36]	0.5689712982396555,
Out[36]	0.561386811540064,
Out[29]	0.5818759209001962,
Out[36]	0.5999231443788183,
Out[11]	0.4735903250210751,
Out[29]	0.4422451210214417,
Out[29]	0.367443863956617,
Out[29]	0.3464749341752949,

T able 3 O utput of the network using RMSE with DB[2]

Number of iteration: 1014
Neural output	The Maximum output value of Z	The desired output
Out[11]	0.9162680773411502,	11
Out[11]	0.9344718889005962,	11
Out[11]	0.9644916602415049,	11
Out [11]	0.9834806635501654,	11
Out[11]	0.9778807487386743,	11
Out[11]	0.9751311957582139,	11
Out[11]	0.95422899811057,	11
Out[11]	0.9881194026530978,	11
Out[11]	0.9222711888589525,	11
Out[11]	0.914371431755235,	11
Out[22]	0.28982386963199785,
Out[22]	0.1603631921941553,
Out[22]	0.4261688532267798,
Out[22]	0.1534632194064746,
Out[22]	0.2269901700229984,
Out[22]	0.061942336470254676,
Out[22]	0.12694752355073993,	impostor
Out[22]	0.3108495756377728,
Out[22]	0.15119936355950758,
Out[22]	0.1686441584877414,
Out[22]	0.0951366298641713,
Out[25]	0.11478804968724104,
Out[22]	0.13450987528872044,

T able 4 O utput of the network using B hattacharyya distance with DB [2]

Number of iteration: 386
Neural output	The Maximum output value of Z	The desired output
Out[11]	0.8961433181197214,	11
Out[11]	0.8638819637059376,	11
Out[11]	0.9217571318947058,	11
Out [11]	0.9748801193094075,	11
Out[11]	0.9648339495699275,	11
Out[11]	0.9624563269068437,	11
Out[11]	0.8842623385642001,	11
Out[11]	0.9794964208997792,	11
Out[11]	0.8979682251746025,	11
Out[11]	0.8733918812082441,	11
Out[22]	0.4250304371519197,
Out[22]	0.3025048721751227,
Out[22]	0.3177051934261649,
Out[22]	0.4280976651324262,
Out[22]	0.316674039652181,
Out[22]	0.15991932091677402,
Out[22]	0.21879182945851217,	impostor
Out[22]	0.4634706111633256,
Out[22]	0.36239391835236484,
Out[22]	0.41319123681756287,
Out[22]	0.24061764756161622,
Out[25]	0.09326042764705673,
Out[22]	0.31606141393564463,

The following curves show respectively the rate of recognition in testing BD[1] and DB[2]. And also the time (in Millisecond) needed to train the BPNN using RMSE and Bhattacharyya.

Time oftraining                    rate of recognition in the two

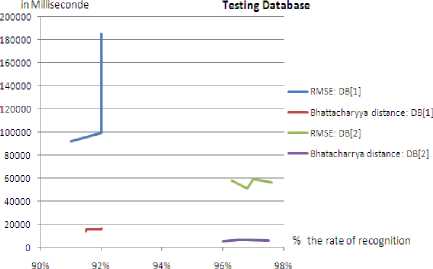
Figure.4 the time (in Millisecond) needed to train the BPNN using RMSE and Bhattacharyya distance.

The experimental results indicate that faces can be recognized swiftly when training our network considering a total error calculated using Bhattacharyya distance.

• VI.    Conclusion

Traditionally in MLP, the total error considered to train the network is the mean square error (MSE) based on the Euclidean distance measure. In this paper, we propose the use of another total error calculation based on Bhattacharyya distance. The effect of the considered error appears clearly since the Euclidean distance does not take into account the correlation of its feature attribute. Indeed, the proposed method applied on the experimental dataset accelerates the learning process and result fast convergence without significant distortion of results comparing to the use of the MSE.

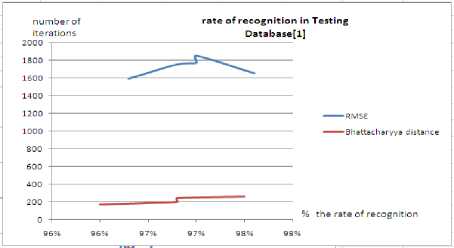
Figure.2 Rate on recognition in DB[1]

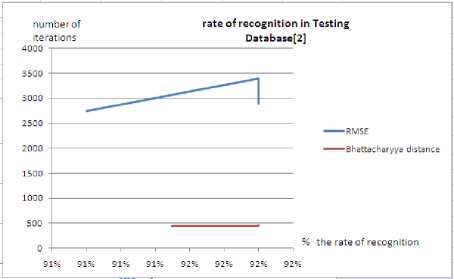
Figure.3 Rate on recognition in DB[2]