Learning the Related Mathematics to Cryptography by Interactive Way

Published Online March 2012 in MECS DOI: 10.5815/ijmecs.2012.02.02

Some people believe that “theory” is far from today's life. They think also that some mathematical topics are tedious to be learned. The realization of multimedia applications for the scientific distribution would play a fundamental role in helping students in understanding the connection between theory and its multimedia application. The most common utilizes of technology in education come out in the form of learning interactive tools. Using these interactive tools is a very good complement to traditional learning via notes, books, etc[1]. We have found many studies, research and development such as multimedia applications, online tutorials and web application facilitate the way of educations using computer technology [2].

We can say that reading by exploration or navigation of a hypertext is interactive. The reader makes visual sweepings and searches of fragments of interest. Using textual or graphical tools that allow the user to identify and to differentiate the contents of the hypertext in order to help navigation is highly recommended [3].When we use via multiple media formats to present the information, it will improve experience of the users and the process of learning. Using this type of interactive tool in an education will stimulate the students' interest and enhances their motivation [4].

Through interactive tools and interaction, students are able to analyze and learn complex theories in a short time. They might get amused at it. Nevertheless, the realization of interactive tools for scientific dissemination may require a deep analysis of contents and didactical paths, in order to choose the best and suitable methodology that favors a higher learning and knowledge level.

In the mathematical concepts and algorithmic procedures in the classroom is frequently difficult to describe. When the lecturer is an artist and can explain the subject with different coloured chalks and explaining around the picture in the board or teaching using well prepared slides presentations. The students can understand little more than static explanations. In this case, using a good graphic interface environment will surely be a helpful for a better understanding of the mathematic concepts or how we can implement the algorithms [2].

During the last years, visualization software tools are increasing and becoming very popular and used in the education purpose, as a lot of publications have been done in educational conferences and journals.

We have taught by an interactive tools since four years. Its aim is to offer people the possibility of focalizing on some mathematical matters and applications starting from daily events intrinsically linked to not trivial results of the scientific research, in the conviction that it stimulates people’s curiosity and make them desire to go deeper into mathematics theories. It is being used by lecturer on the class lectures and students when they want to learn by themselves.

We will analyse the main requirements for these interactive tools should carry out to be helpful for both lecturers that are not coming from computer area and the students in the first subject and we will present the advantages of these Interactive tools for mathematics learning that provide in learning processes [6].Using these kinds of tools in the class allows to visualize concepts, as well as to show a great number of examples in little time. The saved time can be used to do active learning activities.

• II.    OBJECTIVES

Our objective of this work is to present our experience on using these Interactive tools for mathematics learning in the teaching and learning ways. We will give a description for both from the didactical and the technological points of view of the interactive tools to be used by lecturer in the class and by students when they want to learn by themselves. To make it as friendly and attractive for students as possible, we are using special attention to the following properties of these tools:

• •    A graphical interface for the hypertext which can be easily handled by the user. It allows the visualization of the contents and the organization of the information in an immediate way through pulldown menus. One of our goals is that the different applications which are presented in the tutorial can be easily and quickly found within each section.

• •    Facility to include new functionalities and algorithms in the future, if desired.

• III.    MULTIMEDIA FACTORS

Multimedia factors are usually used to describe a topic and illustrate it using visualization of objects and processes. They mostly enable to test the explained matter using several prepared exercises as well.

We consider multiple factors in this work having effects on learning which are:

• •    Visual and auditory inputs: They are often considered to be of great assistance in providing more effective learning outcomes. However, learners have to divide their attention across multiple inputs when presented with instruction in both auditory and visual modes. We believe that if learners focus their attention on one single media resource at a time have better results than those to whom more complex delivery has been offered.

• •    Interaction : It is important to distinguish between functional interaction and learning interaction. The first one includes functions like volume control, audio and video queuing, search tools, navigation, and configuration parameters. The latter is interaction provided for specific learning outcomes.

• •    Learner styles : Multiple views of information can be provided rather than assuming a single information structure. This way of presenting information supports effective alternatives for different learning styles.

• •    Content delivery and content exploration : Content delivery refers to educational materials like textual course notes and other supporting media where learners go through the course materials in a way they do in distance education. Content exploration has more interactive fashion such as simulations, games and other complex environments. At the same time interactive systems should facilitate various learner styles and provide opportunities for learner control.

• IV.    DESCRIPTION OF INTERACTIVE TOOLS

Modular Arithmetic, already well-known by the old Greek and Chinese mathematicians, has found its greatest applications in the second half of the 20th century, with the appearance of Computer Science. They have found its best applications especially with the invention of public key crypto systems. This interactive tool focuses on its theoretical and practical aspects as well. A lot of examples are included in the tools. It has been implemented using web technologies [6].

This interactive tutorial focuses on its theoretical as well as on its practical aspects. Numerous examples are included, as well within the texts as in the form of interactive applications for the World Wide Web. These applications have been implemented using technologies characteristic of the Web [1].

The below figure shows the home page of the tools where the reader can access the different sections that we will describe later.

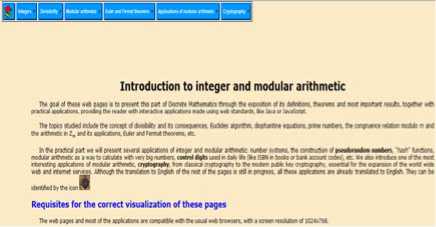
Figure 1. Home page of the tutorial.

The structure of the application is showing into the following pull-down:

• •    Integers: In this theoretical section we described the basic concepts about the integers and the induction principles.

• •    Divisibility: Divisors and multiples - Greatest Common Divisor (GCD) - Prime numbers. These theoretical concepts are complemented with applications to change the expression of numbers in decimal basis to other basis, and to calculate the GCD of two numbers using Euclid algorithm, or to

• •    find prime numbers in a given rank using the Sieve of Eratosthenes.

• •    Modular arithmetic: Congruence relation – Modular exponentiation. Modular Arithmetic is introduced from the congruence relation, showing next the methods to solve linear congruence equations and congruence systems. All this is also supported by some applications that show the most common operations in Modular Arithmetic, the fast modular exponentiation and an application to solve systems of congruence equations.

• •    Euler: Primarily tests and the usual methods to generate big prime numbers are also presented. A very interesting application of the notions studied so far is the cryptosystem RSA.

• •    Applications of modular arithmetic: Arithmetic with big numbers – Random numbers – Hash tables. The tutorial shows several very important applications of the calculus with congruencies in Computer Science, like the Arithmetic with very great numbers, the simple generation of random numbers in a computer science system.

• •    Cryptography: Introduction to cryptography – Information security – Cryptology – Public key and private key cryptosystems. The last part of the application is devoted to one of the most important applications of Modular Arithmetic nowadays: Cryptography. An historical introduction is included. Different cryptosystems, like Cesar cipher or poly alphabetical substitution are presented, along with their corresponding to practice coding with them. Finally, the most important public key cryptosystem, the RSA algorithm, is studied. This algorithm uses as encryption and decryption transformation the operation of modular exponentiation. Its security is based in the computational complexity that supposes the factorization of the product of two big prime numbers.

We describe next some of the function:

• A.    Sieve of Eratosthenes

In order to illustrate the section dedicated to obtain prime numbers by means of the Sieve of Eratosthenes, small function has been made. Prime number is a natural number that has exactly two distinct natural number divisors : 1 and itself. In this system will show how to check if the number is prime or not. We enter the number then we press the button. it will print if it is prime.

Check if N is prime!

Enter a positive integer N

IS N prime? j

Yes

What is a prime number? ]   [ Reset [

Figure 2. Checking the prime number.

• B.    Factorization

It is the decomposition of an object (for example, a number, a polynomial, or a matrix) into a product of other objects, or factors, which when multiplied together give the original. In our system, it will show the factorization of the positive integer number. We enter the number then we press the button. It will print the factors.

Factorization

Enter a positive integer

Is

18 = 2*3A2

The factorization uses the notation aAb which means ab.

Figure 3. Checking the factorization of number.

• C.    Euclid algorithm

This algorithm will help us to find the Greatest Common Divisor (GCD) which is two or more non-zero integers. It is the largest positive integer that divides the numbers without a remainder. This application shows the steps followed in Euclid algorithm to find the greatest common divisor (GCD) of two positive integers a and b. Moreover, the system computes a solution for the Diophantine equation aX + bY = gcd (a,b).

Greatest Common Divisor

Enter integers A and В

A = S14

В z: 502

C4lo*ie

SCO = 2

Example                Rexel

Figure 4. Checking the GCD of two numbers.

There are two text fields to enter the numbers whose greatest common divisor we want to compute. There is an activation button to tell the system to begin the execution of the algorithm from the entrances indicated in the text fields. Finally, there is an output text window to show the greatest common divisor of a and b, and the particular solution obtained for the diophantine equation aX+bY = gcd (a, b).

• D.    Modular Arithmetic:

This section designed to show how to do the more common operations in Modular Arithmetic. The user must write a number and press mod and the write the mod number. The system will print the result.

Figure 5. Calculation the modular arithmetic.

• V. USER EVALUATIONS OF THE TOOL

Students evaluation was conducted to determine students' perception on the usability aspect of the tool. The instrument was adapted from [14] and [15]. The instrument covers four dimensions: learnability, usefulness, ease of use and outcome/future use.

• A.    Instrument for User Evaluation

For students evaluation, a set of questionnaire which comprises of students evaluation sections was used. The students evaluation section is intended to collect data on students' opinion regarding the interactive tool usability aspects. A 5-point Likert scale anchored by "Strongly Disagree" (1) and Strongly Agree (5) was used.

• B.    Method for User Evaluation

The students evaluation was conducted on two classes of thirty respondents. Respondents consist of male and female. Each respondent was given brief explanation regarding the usage and the user interface of the tool. Each student was allocated ample time to try and explore the content of the tool. Once they were done, students were given a questionnaire for students evaluation.

• VI.    RESULTS

Descriptive statistics, reliability analysis and t-test were used in this study. SPSS version 16 for Windows was used to analyze the data. Results from the descriptive, reliability, and t-test analyses will be discussed in the following section.

As far as the gender is concerned, 20 (66.6%) of the respondents were males and 10 (33.3%) were females. A minimum of eight users are required for reliable measures for each variance in the data. Thus, there is sufficient number of participants for each group [16].

Both validity and reliability were addressed for the usability evaluation questionnaire. The validity of a questionnaire is the degree to which the questionnaire is actually measuring or collecting data about what there searcher thinks it should be measuring or collecting data about. One of the most commonly reliability coefficient used is Cronbach Alpha [17]. The reliability of a questionnaire is the ability of the questionnaire to give the same results when filled out by like-minded people in similar circumstances. It is usually expressed on a numerical scale from zero (very unreliable) to one (extremely reliable) [18].

Thus, Cronbach alpha values were calculated using SPSS 16 to determine the data inter-item reliability which assesses the degree of internal consistency between multiple measurements of a dimension. Table 1 presents the Cronbach alpha value for each measure. The learnability, usefulness, ease of use and outcome/future use measures have Cronbach alpha of greater than 0.7, thus, these measures satisfy the internal reliability criterion.

TABLE I:

CRONBACH ALPHA VALUES FOR ALL DIMENSIONS.

Measure	Number of items included	Cronbach Alpha
Learnability	8	0.759
Usefulness	6	0.710
Ease of use	6	0.732
Outcome/ future use	4	0.778

Usability evaluation from users’ perspective is important in obtaining users’ opinion towards the usability of the tool. The descriptive statistics for all the measures are presented in Table 2. A one-way ChiSquare test of homogeneity was conducted on the responses for all the items. A significant p-value indicates that the responses are not equally distributed across the items. As shown in Table 2, the results are positive with p-values significant at 0.01 for learnability, usefulness, ease of use and outcome / future use.

TABLE II:

DESCRIPTIVE STATISTICS FOR ALL MEASURES.

Measure	N	Mean	Std. Deviation	P (ChiSquare) 1
Learnability	30	4.00594	0.883581	.001
Perceived Usefulness	30	4.516776	0.8319542	.069
Perceived Ease of use	30	4.5177621	0.812	.002
Outcome / future use	30	3.995	0.8691	.062

Table 3 shows the descriptive statistics for all the items. Twelve items with means more than 4 are bolded which indicate that most of the students agreed on these items and just neutral on the rest of the items that are related to the tool. Overall, the results indicate that the students agreed that the tool has good usability.

TABLE III:

DESCRIPTIVE STATISTICS FOR ALL ITEMS.

Item		Mean	Std. Deviation
LEARNABILITY
1	It was easy to learn to use the tool.	4.23	0.761
2	The information provided by the tool was easy to understand.	3.7	0.788
3	The information provided in the tool helped me in learning process.	3.67	0.916
4	It provides clarity of wording.	3.99	0.729
5	Data grouping is reasonable for easy teaching.	4.27	0.860
6	The ordering of information is logical.	4.30	0.961
7	The command names are meaningful.	3.53	0.758
8	It provides no penalty teaching.	3.70	0.956
PERCEIVED USEFULNESS
9	Using (the tool) would enable me to understand the cryptology more quickly	4.26	0.938
10	Using (the tool) would improve my job	3.65	0.984

¹ Significant at the 0.01 level.

	performance
11	Using (the tool) in my studying would increase my knowledge	4.02	0.894
12	Using (the tool) would enhance my effectiveness on the studying	4.21	0.889
13	Using (the tool) would make it easier to do my tasks	3.35	0.973
14	I would find (the tool) useful to understand the cryptography concept	3.77	0.853
PERCEIVED EASE OF USE
15	Learning to operate (the tool) would be easy for me	3.90	0.765
16	I would find it easy to get (the tool) to do what I want it to do	4.19	0.916
17	My interaction with (the tool) would be clear and understandable	4.23	0.784
18	I would find (the tool) to be flexible to interact with	4.33	0.928
19	It would be easy for me to become skillful at using (the tool)	4.09	0.938
20	I would find (the tool) easy to use	3.69	0.842
OUTCOME/FUTURE USE
21	I was able to complete my teaching quickly using the tool	3.69	0.728
22	I could effectively complete my teaching using the tool	4.02	0.894
23	I was able to efficiently complete the teaching using the tool	4.31	0.765
24	From my current experience with using the tool, I think I would use it whenever I need.	3.64	0.729

• VII.    CONCLUSIONS

There are a lot of researches comparing the effectiveness of online learning and of face to face learning, researchers haven’t demonstrated any significant difference. We found a lot of studies that have proved no significant differences between exam results of online students and those of face to face students [7], [8], [9]. However, there are cases in which online learning is reported to be more effective than face-to-face learning [10], while some research findings revealed that face-to-face learning is more effective than online learning [11]. These make us think that the best option is to use graphical and interactive tools in two ways. On one hand, these tools help the teacher in the classroom, while on the other hand, the students can work and experiment with them making their own examples, out the classroom. The didactical benefits of this interactive tutorial for Modular Arithmetic, according to our experience in teaching these mathematical concepts, are:

• -    It helps the student to learn the subject.

• -    It helps the teachers in their lectures by navigating through the examples and the applications implemented along the hypertext.

• -    They offer the student the opportunity to experiment, increasing interactivity.

In conclusion, the tool was evaluated and the results indicate that it was designed with good usability. The learnability, usefulness, ease of use and outcome/future use measures have Cronbach alpha of greater than 0.7. Thus, they satisfy the internal reliability criterion. Results from this study indicate that the multimedia learning environment motivated students to more understand the related mathematics to cryptographic. The findings of this study concur with other numerous studies in the field of multimedia learning [19], [22] and [20]. It is hoped that the findings of this study will encourage us to incorporate interactive way into our curriculum for teaching and learning in order to improve and enhance the students understanding and knowledge regarding related mathematics to cryptographic.

ACKNOWLEDGMENT

The first author wish to thank Dr. Daniyal M. alghazzawi, chairman of Department of Information Systems, King Abdulaziz University, for his support to the staff.