Легирование поверхности металлов с использованием короткоимпульсного лазерного излучения

МАТЕРИАЛЫ И МЕТОДИКА ИССЛЕДОВАНИЯ

Образцы из технически чистых железа и никеля толщиной 8 мм механически полировали и отжигали при температуре 1200оС в течение двух часов вакууме 1,35*10–2 Па. Затем образцы из железа покрывали тонким ~ 1мкм слоем углерода, а образцы из никеля слоем меди с помощью вакуумного поста ВУП.

Приготовленные образцы обрабатывались короткими импульсами излучения рубинового лазера (длина волны излучения λ _изл = 0,687 мкм) в режиме модулированной добротности. Длительность импульсов составляла τ _имп ~ 30 нс. Диаметр пятна излучения на поверхности мишени составлял величину порядка 3,5 мм. Поэтому плотность мощности лазерного излучения оценивалась как ~ 10⁹ Вт/см². Возникновение лазерно-индуцированных ударных волн при таких параметрах импульсного лазерного воздействия было теоретически обосновано и экспериментально изучено авторами работ [1-6]. Механизм возникновения ударной волны в металличекой мишени обусловлен импульсом отдачи испаряюшегося тонкого (~ 0,1 мкм) поверхностного слоя металла. Давление в такой ударной волне расчитанное согласно методике, разработанной авторами работы [6] по эмпирической формуле

/ f ?SJ / J ,-M16 .-(MM

• — 28.561 . _ I x I i I I (1) ^mer * \7-Ю^кВт/см² / \3438mkm# \08чс/ ,(1)

где I_max – плотность мощности излучения, τ _имп – длительность лазерного импульса. Давление в лазерно-индуцированной ударной волне P , рас-читанное по методике [6] составило величину порядка 20 ГПа, скорость механического нагружения оценивалось нами как ~10⁷с^-1.

Электронно-микроскопические исследования поверхности зоны воздействия, проводились на растровом электронном микроскопе PHILIPS. Затем был проведен послойный по глубине зоны термического влияния микрорентгеноспектральный анализ на установке “SUPERPROB-739”.

ОБСУЖДЕНИЕ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ

В результате проведенных исследований обнаружено появление на обрабатываемой поверхности следов эрозии (см. рис.1).

Рис. 1. Электронная растровая микрофотография поверхности никеля с нанесенным слоем меди после короткоимпульсного лазерного воздействия. Увеличение 2000^Х

На микрофотографии имеются следы эрозии поверхности в результате абляции, свидетельствующих о мощных гидродинамических процессах в зоне лазерного воздействия.

В более ранних работах [5, 6] нами аналитически было получено решение уравнения массопереноса в ударных волнах. В этой связи возникает необходимость теоретического ана- лиза кинетического уравнения массопереноса с учетом бародиффузии и термодиффузии

При определенных допущениях и ограничениях лазерно-индуцированную ударную волну можно считать плоской. Рассмотрим процесс транспорта атомов вещества из поверхностного слоя в обьем полубесконечного твердого тела под действием поля напряжения плоской ударной волны и градиентом температуры.

Уравнение массопереноса с учетом бародиф- фузии и термодиффузии можно записать в виде ас „с2с а(кр аp) а (пкт атA

= D + I D—p ■ I + I D ■ I а t     аx ² аx ( p аx J аx V т аx J

Di =

DV о ; D = DQi kT 0 ^{; 2} kT 0²

;

где С – концентрация, D –коэффициент массопе-реноса, Р – давление, К_Р* D – коэффициент бародиффузии , К_T*D – коэффициент термодиффузии.

В операторной форме это уравнение имеет вид

LС = 0 ,                  (3)

где

L =

а ^s² а a p а „ а² p „ а т а „ а ² т

+ D    + D 1 + D i     + D 2 + D 2

а t     а ² x      а x а x      а x ²       а x а x      а x ²

Здесь V _о – парциальный обьем, k – постоянная Больцмана, Т_о – абсолютная температура поверхности образца в момент прекращения действия лазерного излучения, Q₁ – поток тепла.

Уравнение (4) линейное, параболического типа с переменными коэффициентами, решаемое по методу «параметрикса» [5, 6]. Параметрикс в первом приближении можно записать в виде

Г(х, t, g т ) = Z o (x, t, g т ) + Z(x, t, дт ) ,    (5)

• ¹    Cv-vF 1 Cv-jr

Яхг,^^—■      ew~v ~7 -exp- ~ >

Z(x, t, с, t) - 11 Z^x, t, $, T)LZ0(n . ^. Tender, где Zo(x, t, V,t) – фундаментальное решенипе уравнения Фика для полубесконечного образца.

Используя начальные условия:

С ₀ ,0 <  x <  d,

0, x ^ d,

где d – толщина приповерхностного слоя, в котором равномерно распределено вещество с начальной концентрацией С_о, можно найти его концентрационное распределение после лазерного воздействия

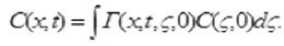
как функциональную зависимость вида

С = С(x, t).                       (7)

При этом, импульс давления принимался в виде солитона, а тепловая волна описывалась ступенчатой функцией Хевисайда:

Г„ A

P ( x, t ) = P,ch                 ,         (8)

V x 0    / где Р - давление, Т - температура, v - скорость распространения ударной волны, х0 – полуширина ударного импульса, © - ступенчатая функци Хевисайда.

Концентрационные распределения меди в никеле, а также углерода в железе показаны на рис. 2. На рисунке также показана кривая аналитического уравнения уравнения массопереноса в ударных волнах.

Образцы из легированных сталей ШХ15, 9ХС и 9Х14 подвергалась лазерному воздействию в режиме модулированной добротности с длительностью импульсов ~ 30 нс и плотностью мощности 109 Вт/см2. Таким образом, создавались условия для генерации ударных волн с давлением во фронте порядка 20 ГПа и скоростью механического нагружения порядка 107с-1, т.е. были созданы такие же условия, как в экспериментах tr* еЗ.

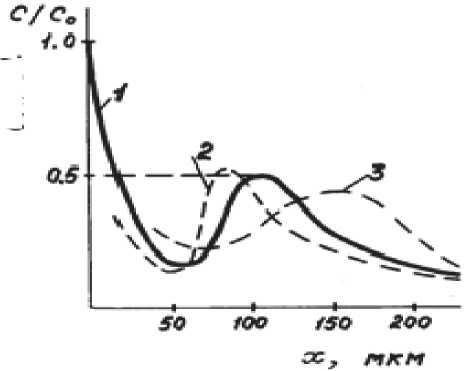
Рис. 2. Кривая 1 – аналитическое решение уравнения массопереноса, кривые

2 и 3, соответственно, концентрационные распределения меди в никеле и углерода в железе по исследованию массопереноса меди в никеле и углерода в железе, описанные выше.

Распределение легирующих элементов по глубине зоны лазерного воздействия представлено на рис.3-5.

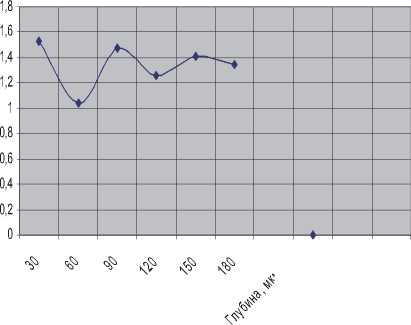
Рис. 3. Распределение хрома по глубине зоны короткоимпульсного лазерного воздействия на образец из стали ШХ15

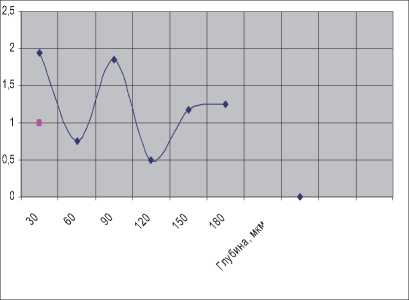
Рис. 4. Распределение углерода по глубине зоны короткоимпульсного лазерного воздействия на образец из стали ШХ15

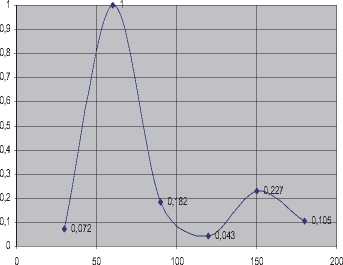
Рис. 5. Распределение углерода по глубине зоны короткоимпульсного лазерного воздействия на образец из стали ШХ15

Из графиков видно, что распределение концентрации легирующих элементов и углерода по глубине от поверхности образца напоминает характер затухающих колебаний. Период такой «волны концентрации» различных элементов составляет от 60 до 90 мкм. Полагая значение продольной скорости звука для железа и сталей равной 6х103 м/с, то при длительности лазерного импульса т = 30 нс в пересчёте на частоту колебаний, получаем значение порядка 108 Гц, что соответствует границе ультразвуков и гиперзвуковых диапазонов длин волн. Известно [7], что граница гиперзвуковых и ультразвуковых колебаний соответствует переходу от тепловых колебаний к механическим (т.е. звуковым) колебаниям. Это можно рассматривать как переход от термической активации процесса массопереноса (т.е. диффузии) к безактивационному (т.е. сдвиговому) движению атомов. Объект массопереноса в этом случае будет – кооперативно движущаяся сверхструктура атомов (кластер), обладающая всеми признаками макроскопического тела. Причина движения такого образования - макроскопические динамические внешние силы (интенсивные внешние воздействия). Понятно, что при таком движении объект массопереноса (кластер) будет зависеть от макроскопических свойств среды, а именно: от сил вязкого сопротивления.

Характер затухания такой волны должен быть связан со сдвиговой динамической вязкостью металла-матрицы (железа или стали). По уменьшению амплитуды можно определить логарифмический декремент затухания L такой концентрационной волны. Из полученных экспериментальных данных следует, что уменьшение амплитуды «волны концентрации» до значения, указанного ГОСТом [8] для различных марок сталей происходит примерно через три периода. Пользуясь известной зависимостью:

L=в Т= 1 /N, (10) где в - коэффициент затухания, Т - период колебаний, N - число колебаний, когда амплитуда колебаний уменьшается в е раз, можно вычислить основные вязкие свойства среды.

Отсюда

β =     .               (11)

NT

Так, используя зкспериментальные данные, т.е. N = 3 и Т = l /с_зв = 6^.10^-5/6^.10³ = 10^-8 с можно определить коэффициент затухания β, который при указанных данных будет равен β = 0,33^.10⁸с^-1.

По коэффициенту затухания можно определить коэффициент сопротивления движению точечного дефекта

R=2m β, (12)

где m – масса межузельного атома ( m ~ 10^-26 кг).

Сила сопротивления пропорциональна скорости движения дефекта. Если считать, что сопротивление вызвано сдвиговой вязкостью, то используя закон внутреннего трения Ньютона, а также выражение (11), можно приближенно записать

β

2 πη_сдв 22

Т ² ρс_з ² _в

где η_сдв – коэффициент динамической сдвиговой вязкости среды. Тогда из экспериментальных данных можно определить этот коэффициент как

βT ² ρсз ² в _~

ηсдв

2π

Из полученных экспериментальных данных он имеет порядок величины ~ 150 Па.с.

Коэффициент кинематической сдвиговой вязкости (фактически коэффициент массопере-носа при сдвиговых процессах) νсдв = ηсдв/ρ для железа и сталей на основании полученных экспериментальных данных ~ 0,02 м2/с.

ВЫВОДЫ

• 1.    На основании данного исследования, а также теоретических исследований, проведенных ранее, установлено, что массоперенос в металлах при короткоимпульсном лазерном воздействии осуществляется путем увлечения межузельных

• 2.    Одной из возможных причин ускоренного массопереноса является каналирование поверхностных слоев обрабатываемого материала и создание условий для экструзирования расплавленного легирующего материала вглубь образца.

• 3.    Продемонстрирована техническая возможность создания в приповерхностных областях обрабатываемого материала слоев с измененным содержанием элементов, а также чередования слоев с повышенным и пониженным содержанием легирующего материала.

атомов в поле лазерно-индуцированной ударной волны. Об образовании ударных волн свидетельствует появление на обрабатываемой поверхности следов мощных гидродинамических процессов.