Лесной пожар на случайном графе со сгораемыми ребрами

Моделирование лесных пожаров в последнее десятилетие приобрело новое направление и новый смысл. Вопросы ставятся не только о том, какой должна быть стратегия тушения пожара, чтобы сохранить как можно больше лесных насаждений, но и о том, какой должна быть оптимальная топология их расположения. Кроме того, эти модели и полученные с их помощью результаты (см., например, [3], [4], [5], [6]) могут быть использованы и в других областях науки и практики, как, например, они применимы для изучения дефолтов банковских систем [1].

В настоящей работе для рассмотрения одного из аспектов распространения лесного пожара используются модели случайных графов, распределение степеней вершин которых является дискретным аналогом распределения Парето [7], [8], [10]. Естественным образом возникает задача оптимизации числа деревьев и топологии их расположения на определенной (ограниченной) территории, обеспечивающих максимизацию числа несгоревших деревьев в случае возникновения пожара.

Рассматриваются случайные графы с N вершинами, степени которых $ _р $ ₂, ..., $_N являются независимыми одинаково распределенными случайными величинами, общее распределение которых имеет следующий вид:

P { $ >  k } = k -^т , к = 1, 2, ., (1) где т > 1 - параметр распределения. При т е (1, 2] распределение (1) имеет конечное математическое ожидание и бесконечную дисперсию,

при т > 2 дисперсия становится конечной. Для построения графа сначала задаются степени его вершин 1, 2, ., N как реализации случайной величины $. Они определяют различимые полуребра графа (полуребром считается ребро, инцидентное некоторой вершине, для которой смежная вершина еще не определена [10]). Ребра образуются посредством равновероятного соединения всех полуребер графа. Сумма степеней вершин может оказаться нечетной, и тогда одно из полуребер графа останется без пары. В этом случае равновероятно выбирается вершина, степень которой увеличивается на 1, тем самым образовав еще одно ребро. Полученный таким образом граф может иметь как петли, так и кратные ребра. Известно, что при N ^ да в графах, распределение степеней вершин которых имеет параметр т е (1, 2), асимтотически достоверно образуется гигантская компонента (см. [7], [10]) - связное подмножество вершин графа, математическое ожидание числа вершин которого пропорционально c • N, где 0 <  c < 1 - некоторая положительная постоянная. В том случае, когда параметр распределения (1) больше 2, гигантская компонента в графе может отсутствовать.

Пусть вершинам графа соответствуют реальные деревья, и, если между вершинами существует ребро, то в случае возгорания одной из вершин по этому ребру огонь распространяется на смежную вершину. Определим зависимость числа деревьев, растущих на некотором ограниченном пространстве, от параметра т. Пусть деревья на этой области расположены упорядо- ченно в виде квадратной решетки размерности 100 × 100. Средняя степень вершины i при полном заполнении будет равна 8, в этом случае при возникновении пожара сгорят все деревья. При значениях i < 8 (рис. 1) часть вершин и ребер графа будет отсутствовать, поэтому некоторые деревья не сгорят.

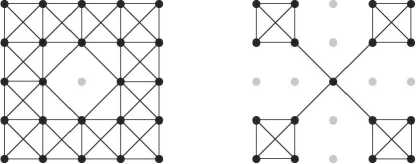
Рис. 1. Топология заполнения решетки при средних степенях вершин графа: i = 7 и i = 4 соответственно

На рис. 1 отсутствующие вершины обозначены серым цветом.

Исходя из приведенных в таблице данных была получена следующая регрессионная зависимость объема графа N от параметра распределения степеней вершин τ (рис. 2):

N = 9256 · τ ^-1,05,                  (2)

с коэффициентом детерминации R ² = 0,97.

Начальные данные для нахождения зависимости N от τ
i	τ	N
1,01	6,75	3350
1,21	2,96	3600
1,33	2,53	3750
1,42	2,32	3900
1,5	2,19	4000
1,6	2,05	4200
2	1,73	5000
2,66	1,49	4780
3	1,42	4489
4	1,29	5578
5	1,23	6700
5,33	1,21	7500
6	1,18	8350
7	1,16	8911
8	1,13	10000

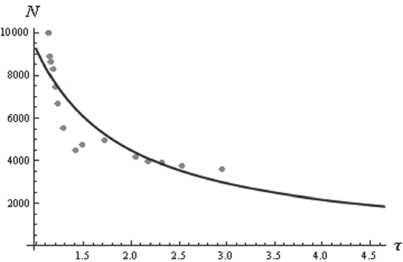
Рис. 2. Регрессионная зависимость N от τ

Применение методов имитационного моделирования в исследованиях случайных графов по- могает продвинуться в понимании тех аспектов, которые теоретически еще не были изучены. В данной работе была использована имитационная модель случайного графа [2], построенная на основе алгоритма, предложенного в [11], с использованием генератора псевдослучайных чисел «вихрь Мерсенна» [9]. Ранее [2] на этой модели (для τ∈(1, 2)) была исследована зависимость структуры таких графов от параметра распределения степеней вершин τ, а также был проведен анализ устойчивости таких графов внешним воздействиям, таким как направленное и равновероятное удаление вершин.

В данной работе рассматривались два типа возникновения пожара. Во-первых, это «случайное возгорание», когда пожар начинается с равновероятно выбранной вершины, во-вторых, «направленный поджог», при котором первой загорается вершина, имеющая наибольшую степень. Цель работы состояла в том, чтобы определить, при каком значении параметра τ распределения степеней вершин графа достигается максимум числа оставшихся после пожара вершин (деревьев). Моделирование графов и вычислительные эксперименты проводились на вычислительном кластере КарНЦ РАН.

Имитационное моделирование проводилось для значений параметра τ из интервала (1, 3,5) с шагом 0,01. Объемы графов N вычислялись из уравнения (2). Для каждой пары значений N и τ генерировалось по 100 случайных графов. После «возгорания» первой вершины все вершины, связанные с ней, считались сгоревшими, и вычислялось число оставшихся (несгоревших) вершин g графа.

При «случайном возгорании» была получена следующая оценка (график зависимости показан на рис. 3):

g = –1476,3·τ2 + 7247,7·τ – 5313,4, где коэффициент детерминации модели равен

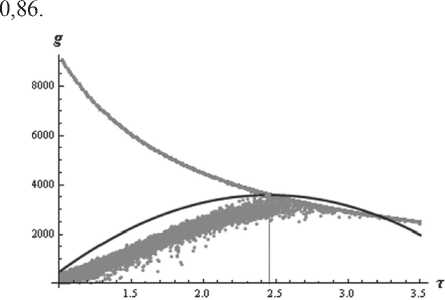
Рис. 3. Регрессионная зависимость числа несгоревших вершин g от параметра τ при «случайном возгорании»

На рис. 3 видно, что при некоторых значениях параметра облако регрессии распадается на 2 части. Это означает, что при одних и тех же значениях τ существует некоторая доля графов, которые почти не сгорают, то есть после пожара в них остается более 98 % вершин. Такая ситуация возникает тогда, когда возгорание начинается с вершины, являющейся частью очень маленькой компоненты связности (не более 5 вершин), и, следовательно, в графе сгорает только эта компонента.

Таким образом, максимум функции при «случайном возгорании» достигается при значении τ = 2,45 (пример структуры такого графа показан на рис. 4). Начальное число вершин графа N в этом случае в среднем составит около 3600 вершин, из которых примерно 3580 выживут после пожара. Средняя степень вершины такого графа i равна 1,36.

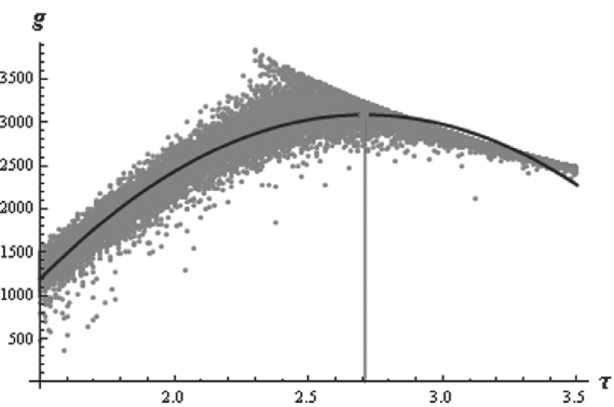
Рис. 5. Регрессионная зависимость числа несгоревших вершин g от параметра τ при «направленном поджоге»

Рис. 4. Пример структуры степенного графа при τ = 2,45

В случае «направленного поджога» была получена следующая зависимость числа несгоревших вершин от параметра τ (рис. 5):

g = –1296 · τ ² + 7025 · τ – 6431, коэффициент детерминации модели R ² = 0,997.

В этих условиях полученная функция достигнет своего максимального значения при τ = 2,71. Тогда N в среднем будет равно 3260 вершин, 3089 из которых останутся после пожара, а средняя степень вершины графа будет равна 1,27.

Таким образом, для того чтобы в случае пожара (как «случайного», так и «направленного») на некоторой заданной территории осталось как можно больше несгоревших деревьев, необходимо, чтобы топология их расположения соответствовала топологии случайного графа с параметром τ распределения степеней вершин (1) от 2,4 до 2,7. Такой граф будет представлять собой многокомпонентную структуру с отсутствием гигантской компоненты связности, средняя степень вершин которой будет колебаться в пределах от 1,2 до 1,4.

Понятно, что предложенный подход к моделированию лесных пожаров не в полной мере адекватен реальности, поскольку распространение огня на соседние деревья зависит от многих факторов и носит случайный характер. Поэтому в следующих наших работах будут рассматриваться ситуации, когда вероятность возгорания ребра меньше единицы.

* Работа выполнена при поддержке Программы стратегического развития Петрозаводского государственного университета на 2012–2016 гг.

FOREST FIRE ON RANDOM GRAPH WITH INFLAMMABLE EDGES