Library of mathematical functions with parallelism at the operational level in the Pythagor language

Introduction . The Pythagor language of functionalstream parallel programming [1–6] maintaining overlapping at the level of operations and assuming the organization of architecture-independent parallel calculations represents alternative approach to parallel calculations. Now the language and its tools are actively developing [7–14]. The article is devoted to realization of mathematical functions library for the Pythagor language and illustrates features of stream parallel calculations with overlapping at the level of operations.

Considerable part of mathematical functions is calculated by means of Makloren's series [15]. Both a faster and less accurate calculations, at which the predetermined number of elements of a series with pre-calculated coefficients, and a less fast and more accurate calculations, at which elements of series are calculated dynamically before achievement of the desired accuracy, are used.

Approximate calculation of mathematical functions and their program realization in a number of the known programming languages are the tasks that have been solved by now. As for the Pythagor language and its original calculation pattern the task has been solved for the first time. Besides, realization of mathematical functions in many known languages is hidden from the developer: he can cause function performance, but cannot know by means of what method and algorithm the calculation of result is done. Thus, the basic principles of mathematical library design described in the article can be useful to those readers who need to solve a similar problem for their own calculation system.

Fast approximate calculation of Makloren's series on the example of a sine, a cosine and exponent. Mak-loren's series for the sine is written as:

sin( x ) ≈ x – x ³/3! + x ⁵/5! – x ⁷/7! + …, where | x | ≤ 1. (1)

In calculation of a sine for a random angle = х radian, it is required to give an argument to an interval [–π, π]. In case the argument belongs to [–π, -π/2) U (π/2, π], it moves to the interval [–π/2, π/2], whereupon remembered is the indicator of the subsequent multiplication of the result by –1. For the argument x from [–π/2, π/2] calculated is х ’ = 2 x /π, approximate formula (1) is written as follows:

sin(x) = sin(πx’/2) ≈ (π/2)x’ – (π/2)3x’3/3! + + (π/2)5x’5/5! – (π/2)7x’7/7! + …, where |x|≤π/2, |x’|≤1 (2)

For fast calculation of an acceptable result the first six summands in a series are taken and their numerical coef- ficients are pre-calculated external to the program code: 1) k1 = π/2 = 1.570796326794, 2) k2 = –(π/2)3/3! = = –0.645964097505, 3) k3 = (π/2)5/5! = 0.079692626245, 4) k4 = –(π/2)7/7! = -–0.0046817541, 5) k5 = (π/2)9/9! = = 0.00016044118, 6) k6 = –(π/2)11/11! = –0.0000035988432.

In the course of the function operation, argument degrees are calculated; multiplication by coefficients and summation of a required formula are performed. Such algorithm is comparable to a similar consecutive imperative algorithm except the fact that the Pythagor language calculation pattern assumes potential parallel performance of all those operations relating to one or different functions with the available input data. Realization of the designated algorithm by means of the Pythagor language forms the following sequences of operators potentially available for parallel calculation (fig. 1).

Fig. 1 shows that a great number of operators of one branch, for example, calculation of argument degrees x2, x3, x5, etc. can be performed only consistently since they need the results of smaller degrees, whereas operators of one layer, for example, «(х2, х5):*>>x7», «(0.079692626245,x5):*>>p3», «(p1,p2):+>>S1» can be potentially available for parallel performance.

When illustrating the graph in fig. 1 selection of auxiliary identifiers was generally used – х2, … х11, р1, … р6, S1, … S5. The program code of function can be realized in the same style, or by means of combining formulas in one expression. For example, calculation of the required sum in the code is written as «(((((p1,p2):+,p3):+,p4):+,p5):+,p6):+ >> return», whereby the operators calculation pattern remains the same (fig. 1). But, for example, selection in the code of identifier x2 is desirable, its existence prevents performing operation 'x*x’ several times when calculating argument degrees.

Comparison of results of a sine fast approximate calculation in the Pythagor language and calculations of a sine by means of a sin function call from math.h library in language C is presented in tab. 1.

Other trigonometrical functions can be calculated similarly via their Makloren's series or by means of substitution of sine values in reduction formulas, for example, of cos (x) =1 – 2sin2 (x/2).

When realizing the mathematical functions library for the Pythagor language, reduction formulas were used. Therefore tables of comparison of cosine and a tangent calculations in the Pythagor and C languages accurately correlate with tab. 1, i. e. for example, cos(1.2) will be closer to a similar call of a cosine from math.h than cos(1.6).

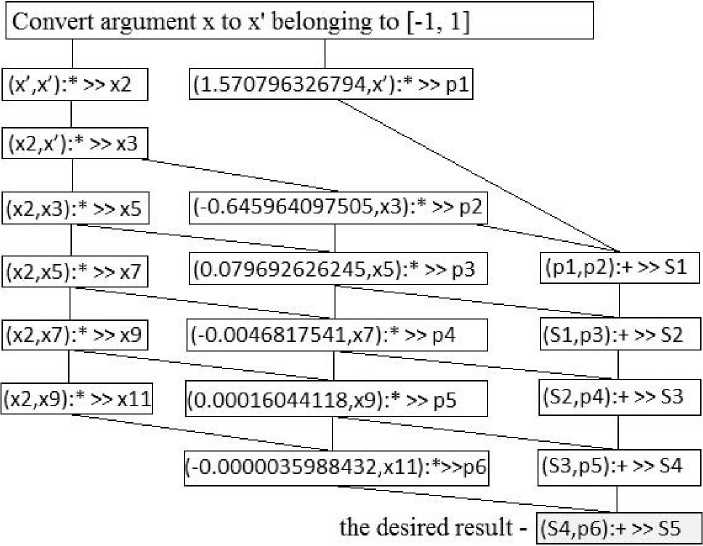
Fig. 1. Simplified information and control graph of the function sin

Рис. 1. Упрощенный информационно-управляющий граф функции sin

Table 1

Sine calculation in the Pythagor language and С language (library math.h)

Argument х	math.h	Pythagor	Argument х	math.h	Pythagor
0.2	0.198668	0.198669	5.2	–0.883455	–0.883455
0.4	0.389417	0.389418	5.4	–0.772766	–0.772764
0.6	0.564641	0.564642	5.6	–0.631268	–0.631266
0.8	0.717355	0.717356	5.8	–0.464604	–0.464602
1.0	0.841470	0.841471	6.0	–0.279418	–0.279416
1.2	0.932039	0.932039	10.0	–0.544021	–0.544021
1.4	0.985450	0.985452	50.0	–0.262375	–0.262375
1.6	0.999574	0.999578	100.0	–0.506366	–0.506370

Under approximate calculation of given functions by means of Makloren's series a considerable decrease in accuracy in the neighborhood of separate points, lying in the series range of definition can be observed, as a rule, it is 1 and-1. The arcsine belongs to such functions. For an arcsine the range of definition of function and series coincide, it is [-1, 1] therefore argument transformation, similar to the one performed to the sine, is not required. Under approximate calculation of an arcsine the following formula based on its Makloren’s series with the coefficients calculated out of the program code is used:

arcsin( x ) ≈ x + 0.166666666666 x ³ + 0.075 x ⁵ +

+ 0.044642857142 x ⁷ + 0.030381944444 x ⁹ +

+ 0.022372159090 x ¹¹ + 0.017352764423 x ¹³ +

+ 0.01396484375 x ¹⁵ + 0.011551800896 x ¹⁷ +

+ 0.009666219208 x ¹⁹ + 0.008390335809 x ²¹ +

+ 0.007312525873 x ²³ + 0.000011679728 x ²⁵, where | x | ≤ 1                       (3)

While for a sine acceptable accuracy it is enough to take first six summands, for an arcsine it is desirable to calculate not less than twelve. In addition, supposing x is located in the neighborhood of points 1 or –1, the accuracy of an approximate formula considerably decreases. In realization of an arcsine for the Pythagor language at x belonging to [–1, –0.93) U (0.93, 1], the auxiliary formula arcsin (x) = π/2 – arcsin is used ((1 – x2)1/2).

Comparison of the arcsine fast approximate calculation in the Pythagor language and calculations of the arcsine by means of the sin function call from math.h library in language C is presented in tab. 2.

When calculating the exponent the following formula with preliminary calculated coefficients based on Mak-loren's series is used:

e^x ≈ 1 + x + 0.5 x ² + 0.166666666666 x ³ +

+ 0.041666666666 x ⁴ + 0.008333333333 x ⁵ +

+ 0.001388888888 x ⁶ + 0.00019841269841 x ⁷, where | x |≤0.7 (4)

Makloren's series of exponent is defined on [–1, 1], but as at fast approximate calculation the final small number of elements is used, for acceptable accuracy the domain [–0.7, 0.7] is chosen. The domain of exponent definition includes all numerical axis, therefore for random argument x the exponent property is used ea+b = eaeb. The argument x is divided into the integral and fractional parts, е in fractional degree is calculated with the help of formula (4), е in the integral degree is calculated by multiplication of constants е or 1/e, at the same time additional values, calculated external the program code, are applied to speed up calculations, for example, е2 = 7.389056098930649, е8 = 2980.957987041726, е64= 6.235149080811582e + 027, used in multiplication.

Comparison of results of fast approximate calculation of exponent in the Pythagor language and exponent calculations by means of an exp function call from math.h library in language C is presented in tab. 3.

The accurate recursive calculation of Makloren's series on the example of a logarithm. Makloren's series for the natural logarithm is written as:

ln(x + 1) ≈ x – x2/2 + x3/3 – x4/4 +..., where –1 < x ≤ 1. (5)

Formula (5) includes higher coefficients than Mak-loren's series of the above considered functions, therefore fast calculation of the natural logarithm is not realized as it would demand enumeration of a significant number of summands (up to several hundreds or thousands). Instead, recursive calculation of formula (5) before achievement of the desired accuracy of 10-8 is used, in imperative language it could be realized by means of a cycle, in the Py-thagor language cyclic algorithms are realized by means of recursive functions.

The definition domain of the natural logarithm is a set of positive numbers, therefore for any argument x the property of the natural logarithm is used ln(b*10a) = ln(b) + a*ln(10) = ln(b) + a*2.302585092994046, where b can be chosen so as to suit the calculation of ln(b) with the help of formula (5).

Recursive function expects the argument type of (number 1, number 2, number 3) where number is b, number 2 in the first recursion call coincides with b, number 3 is a series denominator, in the first recursion call equals one. One iteration of the recursion calculates four summands of Makloren's series. The simplified information and control graph of the natural logarithm function is written as (fig. 2).

The expressions in braces, for example {(S, (b, (b4,b):*, (z,4):+):recursion):+} in fig. 2, belong to the delayed calculations and will be carried out only if the condition of stop is true: - i.e. when the fourth command s4 in the current iteration taken according to module are more than 10-8. Commands (b, (b4,b):*,(z,4):+) form the argument (number1, number2, number3) for the iteration following the same recursive function. Presented here recursive calculation of formula (5) can be realized via Pythagor language tools or other recursion ways, however, when realizing the library of mathematical functions the suggested method was chosen.

Comparison of the natural logarithm in the Pythagor language and natural logarithm by means of a log function call from math.h library in language C is presented in tab. 4.

Table 2

Calculation of the arcsine in the Pythagor and C languages (library math.h)

Argument х	math.h	Pythagor	Argument х	math.h	Pythagor
0.1	0.100167	0.100167	0.91	1.143284	1.140812
0.2	0.201358	0.201358	0.92	1.168081	1.164584
0.3	0.304693	0.304693	0.93	1.194413	1.189442
0.4	0.411517	0.411517	0.94	1.222630	1.229622
0.5	0.523599	0.523599	0.95	1.253236	1.258546
0.6	0.643501	0.643501	0.96	1.287002	1.290796

Table 3

Exponent calculation in the Pythagor and C languages (library math.h)

Argument х	math.h	Pythagor	Argument х	math.h	Pythagor
–25	0.000000	0.000000	0.5	1.648721	1.648721
–13.7	0.000001	0.000001	1.1	3.004166	3.004166
–9.6	0.000068	0.000068	6.6	735.095093	735.094910
–7.9	0.000371	0.000371	8.8	6634.245117	6634.240234
–1.5	0.223130	0.223130	16.3	11994985.0	11994990.0
–0.8	0.449329	0.449329	25	72004902912	72004902912

Table 4

Calculation of natural logarithm in Pythagor and С languages

Argument х	math.h	Pythagor	Argument х	math.h	Pythagor
0.07	–2.659260	–2.659260	15	2.708050	2.708050
0.15	–1.897120	–1.897120	40	3.688879	3.688879
0.47	–0.755023	–0.755023	200	5.298317	5.298317
0.88	–0.127833	–0.127833	400	5.991465	5.991465
1.85	0.615186	0.615186	10500	9.259130	9.259131
8	2.079442	2.079442	100000	11.512925	11.512930

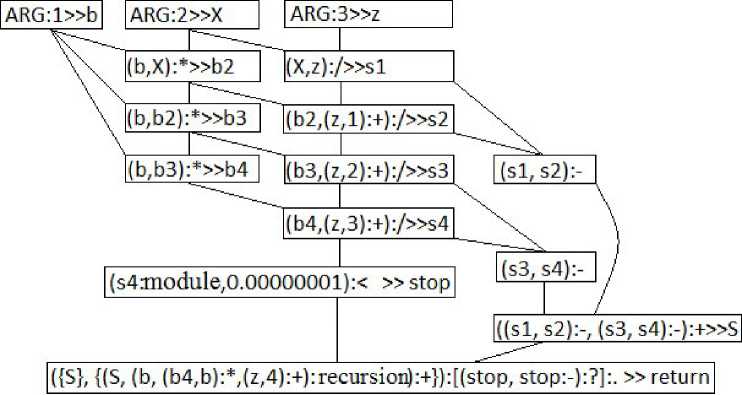
Fig. 2. Simplified information and control graph of the function ln

Рис. 2. Упрощенный информационно-управляющий граф функции ln

Having realization of natural logarithm calculation it becomes possible to calculate a logarithm on a random basis, using log a (b) property = ln(b)/ln(a), for a decimal logarithm in a denominator a constant 2.302585092994046 calculated exclusive the code is substituted. Exponentiation is realized by means of the formula x^y = e^y*ln(x).

Conclusion . The problem of the Pythagor language mathematical library development has been completely realized and is one of the subtasks which are successfully executed with the RFFI grant “Architecture-independent Development of Parallel Programs on the basis of the Functional and Stream Paradigm”.

The list of the realized mathematical functions. Module. Sine. Cosine. Tangent. Cotangent. Arcsine. Arccosine. Arctangent. Arc cotangent. Secant. Cosecant. Square root. Cubic root. Rounding. Rounding down. Rounding up. Integral and fractional parts of number. Exponent. Hyperbolic sine, cosine, tangent, cotangent. Natural logarithm. Decimal logarithm. A logarithm on the specified basis. Exponentiation. The integral part from division and a remainder of division (arguments of function can be numbers, both integral, and material). Mantissa and exponent of the two marking. Multiplication of number to the power of two. Number sign. Inverse hyperbolic: cosine, sine, tangent, cotangent, secant, cosecant. Rising of the two to the power. Maximum from couple of numbers. Minimum from couple of numbers. Hypotenuse. Difference module.

All realized functions are included in the open repository of the Pythagor language, thus, the developer can not only execute and look through their code, but also borrow it for creation of own algorithms or alternative realization of mathematical functions.

Acknowledgment. This work was carried out under financial support of RFFI within the framework of the scientific project № 17-01-00001.