Linear antenna array pattern synthesis using elephant swarm water search algorithm

Published Online March 2019 in MECS

One of the main advantages of the use of antenna array, rather than of only single elements, is that the major-lobe direction and side-lobe level of radiation pattern are controllable [1]. For antenna array, the radiation pattern is function of the magnitude and the phase of the excitation current and the position of each array element [2]. Finding these parameters to obtain a desired radiation pattern is the primary concern in the pattern array synthesis [3].

The problem of synthesizing patterns has drawn much attention over the years. Many analytical methods have been proposed for its solution [4]. Examples of analytical techniques include the well-known Taylor method and the Chebyshev method [5]. In many applications, the synthesis problem of an antenna array consist of finding an appropriate set of amplitude and phase weights that will yield the desired far-field pattern with an equally spaced linear array [4], [11].

However, it is well known that the antenna performance related to the beam width and side lobes levels can be improved by choosing both the best position and the best set of the amplitude and phase for each element of an unequally spaced array [4]. The global synthesis of antenna arrays that generate a desired radiation pattern is a highly nonlinear optimization problem. Therefore, lots of computational efforts have been already used [6], [7] for this purpose. Classical optimization techniques used for array pattern synthesis need a starting point that is reasonably close to the final solution, or else they are likely to be stuck in local minima [2]. As the number of parameters and, hence, the size of solution space increases, the quality of the solution strongly depends upon the estimation of initial values. If the initial values fall in a region of the solution space where all the local solutions are poor, a local search is limited to finding the best of these poor solutions.

Because of the disadvantages of these classical optimization techniques, in the past decade, techniques based on metaheuristic have received much attention for solving the array pattern synthesis problems. Metaheuristics are the one of the well-accepted subclass of optimization techniques [8], [9]. Here, optimization processes are inspired by different physical phenomena or animals and insects’ behaviors or evolutionary concepts. The main reasons behind attractiveness of metaheuristics are simplicity, flexibility, derivation-free mechanism and local optima avoidance capability [10]. These important properties help metaheuristics greatly suitable for application in real-life optimization problems.

Different metaheuristic or their modification algorithms have been used like genetic algorithms [12], simulated annealing [13], differential evolution algorithm [14], bacterial foraging algorithm [15], plant growth simulation algorithm [16], Taguchi’s and self-adaptive differential evolution [17], biogeography based optimization [18], bees algorithm [19], particle swarm optimization [20], [31], cuckoo Search [21], Seeker optimization algorithm [22], invasive weed optimization [23], harmony search algorithm [24], firefly algorithm [25], evolutionary search algorithm [26], differential search algorithm [27], cat swarm optimization [28], hybrid cuckoo search [29], backtracking search optimization algorithm [30] etc for linear antenna array pattern synthesis problem. Many of them gave very satisfactory results. However, No Free Lunch theorem [32] states that there is no single metaheuristics which is suitable for solving all kinds of optimization problems. Therefore, looking for different competitive and efficient metaheuristics for linear antenna array synthesis is still a fascinating and open issue in this field of research.

Elephant Swarm Water Search Algorithm (ESWSA) [33], [34], [35] is a recently proposed metaheuristic which is inspired by water resource search procedure of elephants during drought. The metaheuristic is very simple in nature. As there are only a few parameters needed to be set in ESWSA, the metaheuristic can be applied easily and less concentration can be given to the parameters tuning of it. So far, basic ESWSA was applied have been applied on many problems in different disciplines, such as three-bar truss design problem [34], spring design problem [34], reverse engineering of gene regulatory network [33], and modeling of welding process [35].

In this paper, this recently proposed ESWSA optimization technique has been used for linear antenna array synthesis problem to achieve desired radiation pattern and the performance is also compared with others existing techniques. Moreover, we have also observed which type of controlling technique (using ESWSA) is suited better for this type of linear array antenna synthesis problem. The rest of this paper is structured as follows. Section II describes the mathematical description of the present problem of linear antenna array synthesis and elaborate two benchmark problem in this research field. The ESWSA is elaborated in section 3. Next, simulated results and discussions are given section 4. Finally, Section V concludes this paper followed by the references.

• II.    Problem Formulation

For a linear antenna array with M elements located throughout the x-axis, the far field array factor (AF) can given as [30]

AF(6) = X m=1 1 m e ^,xk5ms™⁶⁺ ^^m) ,      (1)

where 6 is the scanning angle, к is the wave number (k = 27"), Л is the operating wavelength. Im, 5mand ^m Л are the excitation amplitude, position and phase of the m-th elements of the antenna array.

When the elements of the linear antenna array are situated symmetrically and excited around the array center and the number of antenna array elements is even i.e. N = M/2, the array factor can be formulated as following way [30]:

AF(6) = 2Lm=1Imcos(k5m sin6 + ^m).  (2)

For a linear antenna array with even number of equidistant elements (see Fig.1) with inter-element spacing d, the 5m can be calculated as the following equation [21]:

5m = (m - 1) d where m = 1,2,......,N.  (3)

On the other hand, for a linear array with even number of non-equidistant elements (see Fig.2) with inter-element spacing d ( between (i + 1)-th and i-th elements, the 5_m can be calculated as the following equation [4]:

8m = Е™1 dt-^1  where m = 1,2,......, N. (4)

The main aim of the study is to find a set of optimum element amplitude, phase, or position values in order to produce a radiation pattern that is closest to the desired pattern specified by the users [4]. Thus, radiation pattern synthesis is a highly nonlinear optimization problem [21]. The relation between the synthesis problem and the optimization method is defined by the fitness function. Here in this study, two types the fitness functions or problems have been adopted for validation purpose.

The first fitness function C 1 [4], [21] is given by:

C = X66=-90°L(6) , where

_ k(6)+|k(6)|

k(6) = (Mmax(6) — IAF0(6)V)(Mmm(6) — |XF0(6)|).

Here M_max and M_min represent the maximum and minimum amplitude or array factor of shaping region respectively. AF₀(6) is the obtained radiation pattern by the optimization technique. L(6) is not equal to 0 only if AF₀ (6) is situated inside the shaping region.

For this objective function, we consider a symmetric uniformly spaced linier array of 12 rectangular micros trip with quarter wavelength spaced spacing. The mask of the desired pattern AFd(6) of this linear antenna array is shown in Fig.3 and it is defined by [4], [21]:

• -5 dB for - 10° < 6 < 10° -60 dB       elsewhere

0 dB for - 20° < 6 < 20° -20 dB       elsewhere

^M mtn = {

^M max

{

The second fitness function is written as [30]

C2=Z6=-O90O|AFo(6)-AFd(6)|,

where AFd(6) is the desired or initial radiation pattern (array factor). In this case, a -30 dB Chebyshev pattern [30], having 20 equispaced elements with 0.5Л interelement spacing (using excitation current element as given in Table 1), is utilized as the initial radiation pattern [30], as shown in Fig.3.

Table 1. The values of the current element (Im) for this initial Chebyshev pattern [30]

Elements of antenna array (m)	Current element (Im)
±1	1.0000
±2	0.9701
±3	0.91243
±4	0.83102
±5	0.73147
±6	0.62034
±7	0.50461
±8	0.39104
±9	0.28558
±10	0.32561

• III.    Elephant Swarm Water Search Algorithm (ESWSA)

In this work, a new metaheuristic namely Elephant Swarm Water Search Algorithm (ESWSA) has been used to obtain desired mask of radiation pattern or array factor i.e. ESWSA has been used for linear antenna array synthesis.

Mandal et al. [33], [34], [35] initially proposed Basic Elephant Swarm Water Search Algorithm (ESWSA) optimization technique. ESWSA metaheuristics is typically inspired by the intelligent and social behavior of social elephants. This algorithm is mainly based on the water search strategy of elephant swarm during drought with the help of different communication techniques. For simplicity, following four simplified and idealized rules are used to develop Elephant Swarm Water Search Algorithm (ESWSA).

• 1.    During drought, elephants are roaming around the ground in search of water in several groups, known as elephant swarm. For an optimization problem, each elephant group of the swarm is analogous to a solution of the corresponding problem. Each elephant group is recognized by its particular velocity and position.

• 2.    The leader takes responsibility to communicate with the other groups of the swarm about the quantity and quality of the water resources which is found during search. For a maximization problem, the fitness value is directly proportional to the quantity and quality of the water resources.

• 3.    Each elephant group memorizes the best location of water sources which was discovered by own group itself (known as local best solution). They also remember best location of water source discovered by all groups (known as global best solution) so far. The elephant group can

• 4.    Water search in nearby and far area (local and global search) is controlled by a probabilistic constant called Switching Probability p ∈   [0, 1]. The leader of the

move from one point to next location based on these memories i.e. velocity and position of each elephant group are updated gradually.

elephant group takes probabilistic decision to switch between local search and global search.

For d -dimensional optimization problem, the position of i -th elephant group of a swarm (consist of N number of elephant group) at t -th iteration is given as X i _й — (х_;1,х_; 2 , ^ .,x_id) and the corresponding velocity is represented by V^ — (V i1 , v_i2, ...., v_id) . Locally best solution by i -th elephant group at current iteration is given as ^pU tM ^{- (} P i1 ^, P i2 ^, ^. ^, P id ) ^and global ^best solution is denoted by G fr _estd — (G 1 , G 2 , ...., G ^ ). Initially, the elephant group are randomly placed throughout the search space i.e. position and velocity are randomly initialized which served as the population of the metaheuristic. As iteration proceeds, the velocities of the elephants groups are updated according to following equations depending on the Switching Probability p .

VU  = Vu * yt + rand(1, d) О (GbeSt,d - xt,d) (11)

if rand >  p [for global search]

Vit+1 = Vu * ^ + ТОпД^Д) О (pbest,i,d - Х1Д) (12)

if rand ≤ p [for local search]

where rand(1, d) is a d -dimensional array of random values within [0,1] and О denotes element wise multiplication. t is the inertia weight at current iteration to balance between exploration and exploitation. It changes according to the following equation

• 1    _ ,.        f^max—^min) „ _f         ПОЛ

• <У -^max-)fXl        (13)

Lmax where tmax, штах, Mmin denote the values of maximum iteration number, upper boundary and lower boundary of the inertia weight respectively. Then, the next position of an elephant group is updated according to following equation.

Xiy-Vf^+X^          (14)

After completion of all iteration, the elephants will reach to the best water resource position found by the swarm that denotes the best solution for the optimization problem.

ESWSA helps to minimize above mentioned two fitness functions (Eq. 5 or Eq. 10) by selecting optimal or best set of amplitude, phase and distance of the antenna elements so that error between desired and obtained radiation is minimized.

Start ESWSA

Define N. d, t_max,X_max, X_min, p and objective function f ;

for i =1 to N

Initialize X_t4 and V_t4 ;

P bestid = X iid ;

end;

Evaluate fitness value f(X_iid) using Eq. 5 or Eq. 10;

G bestid = ^min Cf)

Assign value of to¹ according to the weight update rules using equation 13;

for t = 1 to tmax for i=1 to N if rand > p

Global water search or update the elephant velocity Viid using equation 11;

else

Local water search or update the elephant velocity V_{ii d} using equation 12;

end if;

Update the position X_iid using equation 14;

Evaluate fitness value for f(X_iid);

P b _e stid =X iid ;

end if;

if f(PL stiiid) < ftfU t.d )

F         pF

^Gbestid     ^Pbest _l i _l d ;

end if;

end for;

X* = Gbestid- end for;

^{Return X}* and f ^(Gbesti d )

End ESWSA

• IV.    Numerical Results

A radiation pattern must have low Maximum Side-lobe Level (MSL), Null Depth Level (NDL), Half Power Beam Width (HPBW) and First Null Beam Width (FNBW) placed in desired directions. Three types of controlling process have been used to achieve desired radiation patterns or antenna array synthesis. First, radiation pattern are obtained by controlling the amplitude only where initial phases and inter-element spacing are fixed. Next, the array pattern is achieved by controlling phase only where initial amplitudes of the elements are and inter-element spacing are assumed to be fixed. In the third case, only the element positions or spacing are controlled where initial amplitudes and phases of the elements are assumed to be constant.

We have considered four important parameters: MSL, NDL, HPBW and FNBW to observe how the ESWSA performed for each case of two problems using different controlling procedure.

All the techniques are simulated using Matlab 2013b in a computer with 2 GB RAM, Dual Core processor and Windows7 operating System.

• A. Case-1

For case-1, we have considered a symmetric linear antennas array of twelve (here 2 N =12 i.e. N =6) rectangular micro-strip antenna [21] with operating wavelength of 10 GHz. Here, ESWSA has been deployed to minimize the objective function -1 as per the Eqn. 5 such that the achieved radiation pattern should remain within the desired or given mask (as Fig.3). In this case, the number of search variable is 6. For ESWSA, the number of population and number of maximum iteration are set to 50 and 5000 respectively. The value of switching probability has been set to p=0.6.

For amplitude only control, the antenna elements have uniform quarter wavelength spacing (i.e. d / =0.25A) [21] and the values of initial phases are considered as zero. The search ranges for the amplitudes are restricted between [0,1]. The obtained radiation pattern or array factor for amplitude only control has been shown in Fig.5 using red colored line. The optimized amplitudes of corresponding current elements obtained by ESWSA are shown in Table 3. It has been observed that the obtained radiation pattern remain within the mask (blue colored) and the MSL is always less than -20dB for amplitude only control which is desirable array factor.

For phase only control, the antenna elements have uniform quarter wavelength spacing (i.e. d i 0.25Л) and the amplitude of initial current elements are considered as one. The search ranges for the phases are restricted between [0, 2л]. The obtained radiation pattern or array factor for phase only control has been shown in Fig.6 using red colored line. The optimized values of corresponding phases of each antenna elements obtained by ESWSA are shown in Table 3. It has been observed that the obtained radiation pattern slightly deviate (at -21°) from the desired mask. Moreover, the MSL for phase only control (-19.51dB) is greater than -20dB for phase only control which is not desirable array factor.

For position only control, the amplitudes of initial current elements are considered as one and the values of initial phases are considered as zero. The search ranges for the inter-element spacing are restricted between [0.1Л, 2Л]. The obtained radiation pattern or array factor for phase only control has been shown in Fig.7 using red colored line. The optimized values of corresponding inter-element spacing of each antenna elements obtained by ESWSA are shown in Table 3. It has been observed that the obtained radiation pattern remain within the mask (blue colored) and the MSL is far below than -20dB for amplitude only control which is desirable array factor.

Table 2 shows a comparative study based on MSL, NDL, HPBW and FNBW amongst different control techniques (for case-1). It is always desirable that the side level is lower as much as possible. It can be observed phase only control procedure has crossed the maximum allowable side lobe level. Position only control has the best performance (i.e. -23.17dB) with respect to MSL.

All control technique has achieved a deep null in the radiation pattern which is very much satisfactory. Position only control has minimum HPBW (i.e. 18.66˚) whereas amplitude only control has lowest FNBW (i.e. 44.16˚). For, phase only control, the radiation pattern outreached the desired mask. Overall, position only control has superior performance for this present problem of 12 elements linear antenna array synthesis using ESWSA, whiles the performance of amplitude only control is also quite satisfactory.

Table 2. MSL, NDL, HPBW and FNBW values obtained by ESWSA for case-1

Parameters	Amplitude only control	Phase only control	Position only control
MSL	-20.15dB	-19.51dB	-23.17dB
NDL	-45.33dB	-77.73dB	-53.90dB
HPBW	19.32˚	19.73˚	18.66˚
FNBW	44.16˚	54.22˚	46.17˚

Table 3. The values of the current amplitude, phase and position of elements for 12 elements array (case-1)

Type of Control	Elements of antenna array
	±1	±2	±3	±4	±5	±6
Amplitude (A)	0.9340	0.2603	0.8763	0.6180	0.1326	0.7224
Phase (rad)	0.1435	0.0882	6.2049	0.9235	5.2358	1.2052
Position (m)	0.0266	0.0145	0.0586	0.0420	0.0397	0.0030

B. Case-2

For case-2, we have considered a symmetric linear antennas array [30] of twenty (here 2 N =20 i.e. N =10) with operating wavelength of 10 GHz. Here, ESWSA has been deployed to minimize the objective function-2 as per the Eqn. 10 such that the achieved radiation pattern matches to the initial 30dB Chebyshev pattern (see Fig.4) [30] as close as possible.. In this case, the number of search variable is 10. For ESWSA, the number of population and number of maximum iteration are set to 50 and 5000 respectively. The value of switching probability has been set to p=0.6.

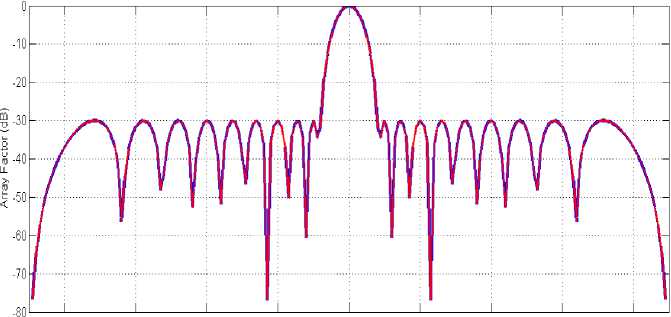
For amplitude only control, the antenna elements have uniform half wavelength spacing (i.e. d j =0.5A) and the values of initial phases are considered as zero. The search ranges for the amplitudes are restricted between [0, 1]. The obtained radiation pattern or array factor for amplitude only control has been shown in Fig.8 using red colored line. The optimized amplitudes of corresponding current elements obtained by ESWSA are shown in Table 5. It has been observed that the obtained radiation pattern exactly matches with the initial 30dB Chebyshev pattern (blue colored) and the MSL is less than maximum allowable side lobe level i.e.-30dB for amplitude only control which is expected.

For phase only control, the antenna elements have uniform half wavelength spacing (i.e. d j 0.5Л) and the amplitude of initial current elements are considered as one. The search ranges for the phases are restricted between [0, 2я]. The obtained radiation pattern or array factor for phase only control has been shown in Fig.9

using red colored line. The optimized values of corresponding phases of each antenna elements obtained by ESWSA are shown in Table 5. It has been observed that the obtained radiation pattern deviate significantly from the desired array factor. Moreover, the MSL for phase only control (-13.86dB) is greater than -30dB for phase only control which is not expected.

For position only control, the amplitudes of initial current elements are considered as one and the values of initial phases are considered as zero. The search ranges for the inter-element spacing are restricted between [0.1Л, 2Л]. The obtained radiation pattern or array factor for phase only control has been shown in Fig.10 using red colored line. The optimized values of corresponding inter-element spacing of each antenna elements obtained by ESWSA are shown in Table 5. It has been observed that the shape of the obtained radiation pattern has been changed completely and the MSL is slightly higher (i.e. -27.75dB) than allowable side-lobe level i.e. than -30dB for amplitude only control which is also not desirable.

Table 4. MSL, NDL, HPBW and FNBW values obtained by ESWSA for case-2

Parameters	Amplitude only control	Phase only control	Position only control
MSL	-30.01dB	-13.86dB	-27.75dB
NDL	-77.23dB	-77.43dB	-77.24dB
HPBW	6.06˚	5.14˚	17.64˚
FNBW	18.16˚	11.84˚	46.04˚

Table 4 shows a comparative study based on MSL, NDL, HPBW and FNBW amongst different control techniques (for case-2). It is always enviable that the side level should be smaller as much as possible. It can be observed amplitude only control procedure has not crossed the maximum allowable side-lobe level while others two have crossed the limit. Amplitude only control has the best performance (i.e. -30.01dB) with respect to MSL. All control technique has achieved a deep null in the radiation pattern which is very much satisfactory. Here, phase only control has minimum HPBW (i.e. 6.06˚) and lowest FNBW (i.e. 11.84˚). For, position only control, both HPBW and FNBW are very large than initial Chebyshev pattern. It is not possible to obtain desired Chebyshev pattern by using both phase only and position only control. Overall, amplitude only control has superior performance for this present problem of 20 elements linear antenna array synthesis using ESWSA.

After considering two abovementioned cases, it has been clearly observed that amplitude only control should preferable for linear antenna array synthesis (to remain within desired mask or to obtain radiation pattern) using ESWSA. The reason behind this important conclusion is that we can achieved desired mask or radiation patter, allowable MSL, satisfactory NDL, feasible HPBW and FNBW by using amplitude only control for all of the two cases (i.e. 12 and 20 elements linear antenna array).

Moreover, we have also compared the performance of ESWSA optimization technique with the others state-of-art optimization techniques like Cuckoo Search (CS) [21], and Particle Swarm Optimization (PSO) [20] for both cases. We have considered the fitness value (final output) as the comparison parameter. Table 6 and 7 show the fitness values for the above mentioned two cases where it can be clearly observed that in all cases of linear antenna array synthesis ESWSA is able to achieve lowest fitness value during the simulation. Therefore, it can be concluded that ESWSA has superior performance over CS [21] and PSO [20]. For this purpose, we have selected ESWSA technique for our present problem.

Table 5. The values of the current amplitude, phase and position of elements for 20 elements array (case-2)

Type of Control		Amplitude (A)	Phase (rad)	Position (m)
Elements of antenna array	±1	0.9537	0	0.0111
	±2	0.9252	6.2748	0.0583
	±3	0.8701	0	0.0231
	±4	0.7925	6.2125	0.0039
	±5	0.6975	6.2832	0.0369
	±6	0.5916	0.1795	0.0408
	±7	0.4812	0.1261	0.0195
	±8	0.3729	0.0017	0.0189
	±9	0.2723	0.0004	0.039
	±10	0.3104	0.0023	0.0222

Table 6. Fitness value comparison for case-1

Technique	Amplitude	Phase	Distance
CS [21]	0	856.61	0
ESWSA	0	853.05	0
PSO [20]	0	5998.23	0

Table 7. Fitness value comparison for case-2

Technique	Amplitude	Phase	Distance
CS [21]	5.62	1158.12	1348.49
ESWSA	0.87	1151.52	1212.41
PSO [20]	673.81	1263.92	1386.29

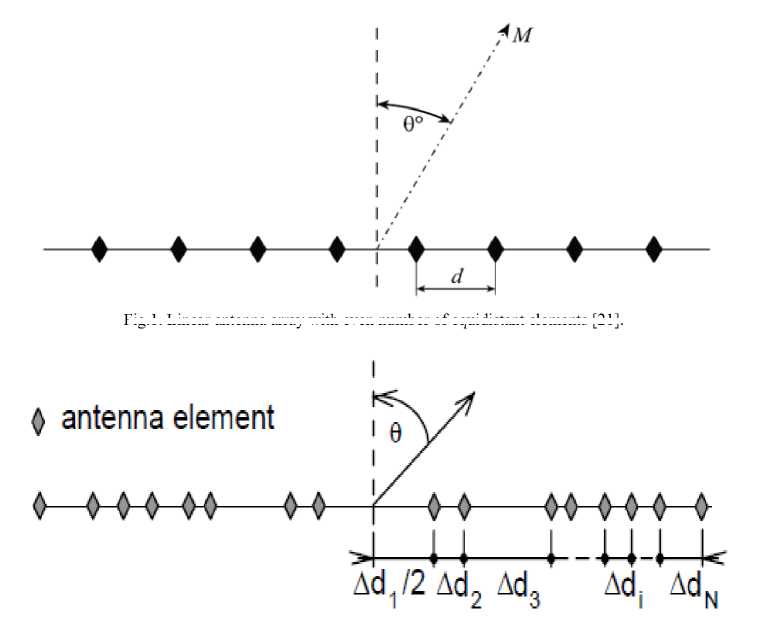
Fig.1. Linear antenna array with even number of equidistant elements [21].

Fig.2. Linear antenna array with even number of non-equidistant elements [4]

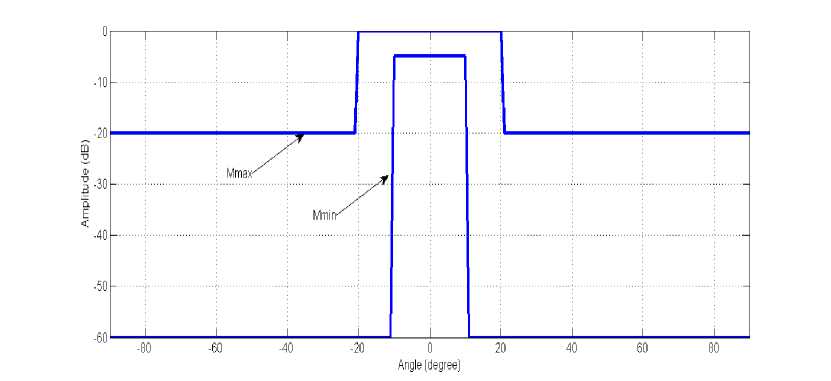
Fig.3. Desired pattern shape or mask for fitness function-1 [4], [21]

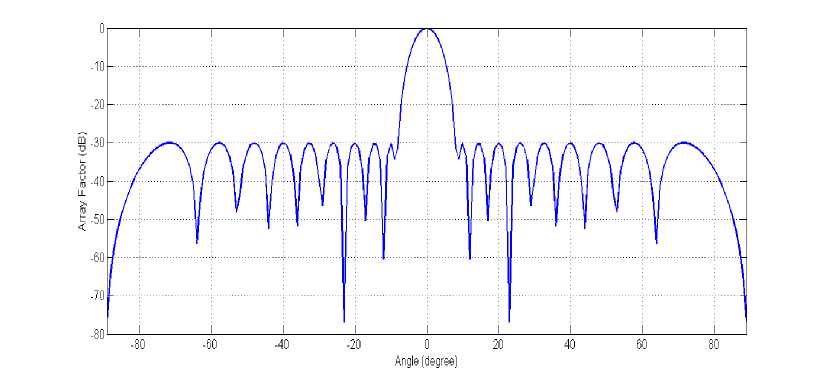
Fig.4. Desired Chebyshev pattern shape for fitness function-2 [30

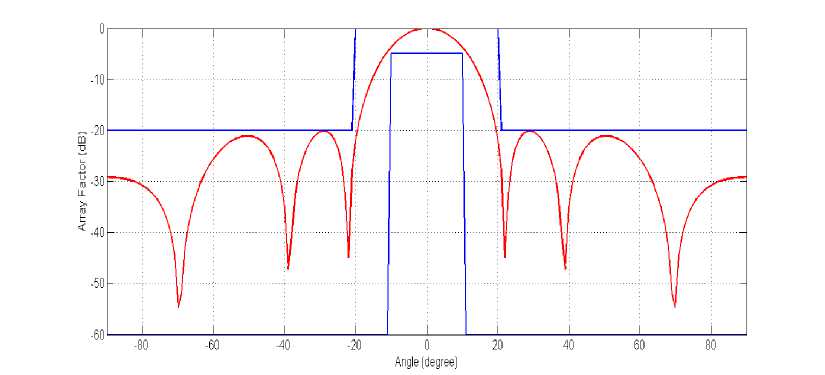
Fig.5. Obtained radiation pattern (red colored) for case-1 using amplitude only control

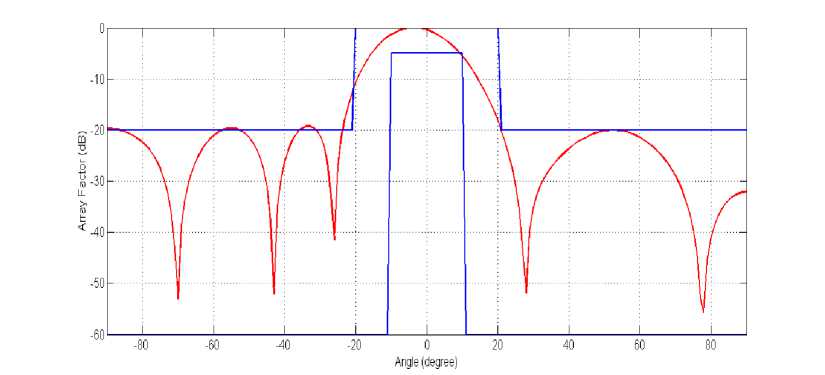
Fig.6. Obtained radiation pattern (red colored) for case-1 using phase only control

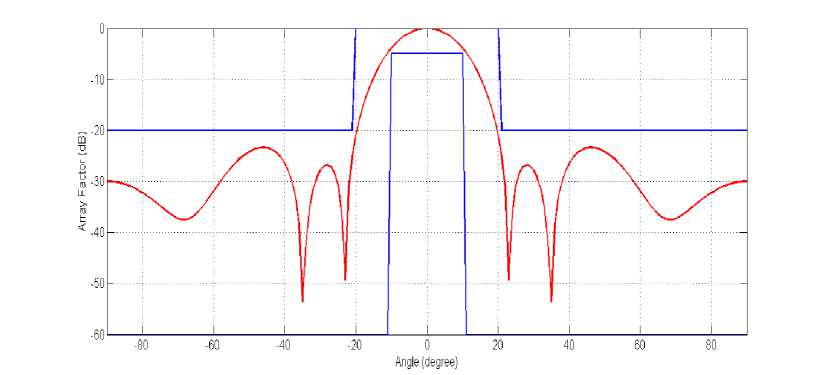
Fig.7. Obtained radiation pattern (red colored) for case-1 using position only control

-80            -60            -40            -20             0             20             40             60             80Angle (degree)

Fig.8. Obtained radiation pattern (red colored) for case-2 using amplitude only control

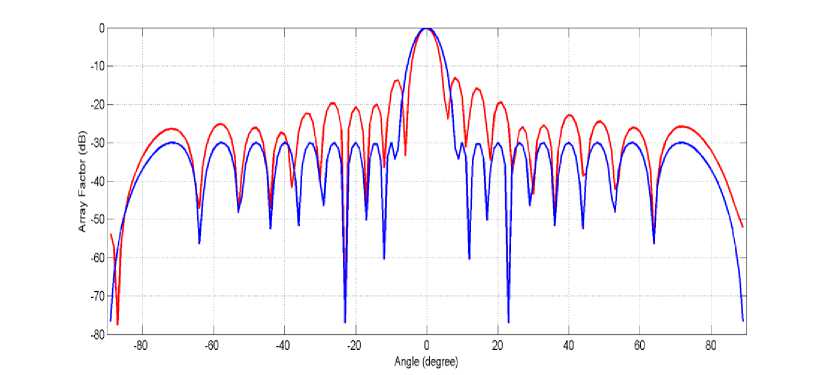
Fig.9. Obtained radiation pattern (red colored) for case-2 using phase only control

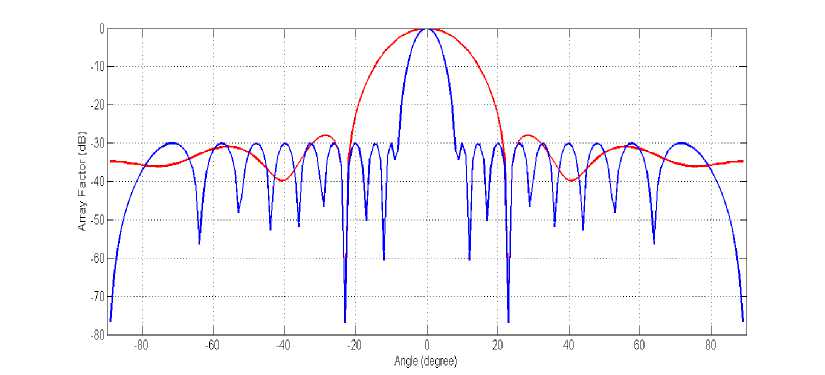
Fig.10. Obtained radiation pattern (red colored) for case-2 using position only control

• V.    Conclusion

Linear antenna array synthesis is very crucial task to achieve the desired radiation pattern for a particular application. In this paper, we have used recently proposed Elephant Swarm Water Search Algorithm (ESWSA) for the present problem of linear array antenna synthesis. ESWSA has been implemented to optimize the amplitude or phase or position of the antenna elements such that the error between desired far-field array factor or radiation pattern or mask with the calculated radiation pattern is minimized. Here, two benchmark problems of antenna array synthesis (12 elements micro-strip patch array with particular radiation pattern mask and 20 elements linear array with initial -30dB Chebyshev pattern) have been considered two validate proposed methodology. Two different objective functions have been used for these two cases. Three different controlling techniques namely amplitude only, phase only and position only are implemented for each case using ESWSA. The obtained results indicate that amplitude only control using ESWSA is most suitable technique for linear antenna synthesis as it can generate desired radiation pattern or remain within the desired pattern mask for all cases. Moreover, ESWSA has superior performance over PSO and CS.

In future, we shall try to increase the efficiency of the ESWSA by modifying or tuning the parameters of the metaheuristic. Moreover, pattern nulling of linear antenna arrays and proposing new objective function for array antenna synthesis are another direction of further research.