Линеаризованная задача устойчивости стержневой конструкции с односторонними связями

Пусть стержневая конструкция с односторонними связями испытывает силовое воздействие, которое может быть представлено в виде двух составляющих. Одна из них, именуемая λ -составляющей и обозначаемая Pλ , меняется пропорционально параметру λ . В исходном состоянии равновесия конструкции составляющая Pλ приводит к возникновению в ее элементах сжимающих продольных сил. Часть Pμ нагрузки, зависящая от параметра μ , то есть ее μ -составляющая, продольных сил в конструкции не порождает вообще или приводит к пренебрежимо малым значениям последних. В частности, при внецентренном сжатии Pλ=P, Pμ=Pe, где P и e – величина силы и ее эксцентриситет соответственно. Обе названные составляющие серьезно влияют на ход решения задачи устойчивости конструкции с односторонними связями и результат решения [1], [2]. О проблемах, которые могут возникнуть при рассмотрении обсуждаемой задачи, в монографии А. В. Пе-рельмутера сказано: «…потеря устойчивости системы с односторонними связями может происходить либо в виде достижения критического значения нагрузки для реализованной в процессе деформирования рабочей системы, либо в том случае, когда ранее нереализуемая (запрещенная односторонними связями) схема закритического деформирования, соответствующая другой рабочей системе, при возрастании интенсивности нагружения перешла в класс реализуемых. При этом само критическое значение, соответствующее такому переходу, может не совпадать с критической нагрузкой ни одной из рабочих систем. Заметим, что явление неустойчивости в большом не может иметь место при отсутствии активной нагрузки (то есть воздействия Pμ в терминологии настоящей статьи. – Ю. Г.), а также при отсутствии зазоров и/или преднапряжения в односторонних связях. Следуя установившейся традиции, мы будем далее называть критическую нагрузку, соответствующую потере устойчивости в малом, верхней критической нагрузкой, а нагрузку, при которой возможна потеря устойчивости в большом, – нижней критической нагрузкой. Во многих случаях явление неустойчивости в большом может и не препятствовать эксплуатации конструкции, поскольку преодоление энергетического барьера требует появления достаточно больших возмущений. Однако этот вопрос следует решать в каждом конкретном случае отдельно. Поэтому, наряду с вопросом об определении верхней критической нагрузки (опасность появления которой еще следует оценить), мы далее рассмотрим и проблему определения нижней критической нагрузки» [3; 95–96].

Итак, с чем приходится сталкиваться при наличии у силового воздействия ненулевой составляющей P _μ , обозначено ясно. Однако в монографии [3] ничего не говорится о том, как оценить вероятность потери устойчивости конструкции в большом и как установить величину энергетического барьера, преодолеваемого при перескоке. Эти вопросы оказались вынесены за рамки указанной работы.

Верхнюю критическую силу обычной конструкции находят при решении линеаризованной задачи устойчивости, тогда как для определения нижней критической силы требуется учет конечности перемещений. При этом наличие воздействия P _μ к существенным осложнениям хода решения задачи не приводит. Но при наличии односторонних связей множество проблем возникают уже на стадии отыскания верхней критической силы. В общем случае задача поиска рабочей системы, теряющей устойчивость, является комбинаторной даже при P _μ = 0, хотя принципиально ясно, что устойчивость теряет та рабочая система, у которой минимальна критическая сила. Если же P _μ ≠ 0, то верхняя критическая сила рассчитываемой конструкции может не совпадать ни с одной из эйлеровых сил рабочих систем конструкции. Чтобы найти такую критическую силу, требуется проследить за процессом деформирования всех рабочих систем.

Однако обсуждать алгоритмы решения комбинаторных задач в этой статье не предполагается. Речь в ней пойдет о том, как можно восполь- зоваться результатами решения линеаризованной задачи устойчивости системы с односторонними связями для оценки вероятности перескока из равновесного состояния, поддерживаемого верхней критической силой, в состояние, реализуемое при нижней критической силе. Рассматриваются начальные состояния, которые при заданных значениях параметров к и ц являются устойчивыми: к < ккр. Далее эти параметры могут меняться по любым заранее оговоренным законам. Это позволяет начинать решение задачи с отыскания рабочей системы, воспринимающей воздействие Рц при Рк = 0 . Способы решения данной задачи известны. Ясно также, как найти спектр эйлеровых сил для конкретной рабочей системы. Далее потребуется лишь наращивать воздействия Рц и Рк по заданным законам и следить за переключением односторонних связей. При каждом переключении происходит смена рабочей системы, и для каждой новой рабочей системы решается задача на собственные значения. Как только какая-либо из рабочих систем потеряет устойчивость, то есть определитель некоторой системы линейных уравнений обратится в нуль, значение кв параметра к фиксируется. Верхняя критическая сила найдена.

Естественно, при определении спектра эйлеровых сил каждой рабочей системы надо следить за тем, чтобы отвечающие этим силам собственные векторы могли реализоваться, то есть отвечали характеру одно сторонних связей. В противном случае линеаризованная задача устойчивости обсуждаемой конструкции не будет иметь решения. Если же решение существует, то вопрос о том, совпадает ли величина к ^в со значением к ^н, характеризующим нижнюю критическую нагрузку, или нет, а если нет, то какой именно рабочей системе отвечает нижняя критическая сила и чему она равна, по-прежнему останется открытым. Возникает потребность в каких-либо априорных оценках величины к ^н .

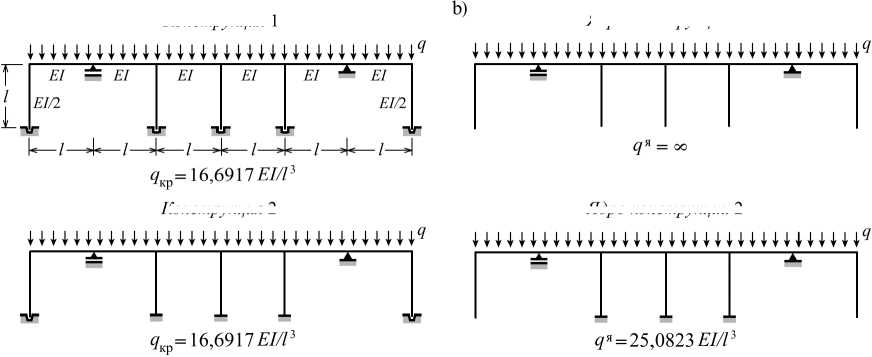
Пусть подконструкция, которая получается при удалении из заданной конструкции всех односторонних связей, является неизменяемой. Такая подконструкция будет далее называться ядром исходной конструкции. Можно ожидать, что критическая сила ядра, характеризуемая параметром кя, приводит к оценке величины нижней критической силы снизу. Во многих случаях это действительно так, но возможны и исключения. Об этом свидетельствуют конструкции, изображенные на рис. 1а. У первой из них все пять стоек оперты на землю односторонне, причем поворотам опорных торцов крайних стоек ничто не препятствует. Точно так же присоединяются к земле крайние стойки второй рамы, тогда как опоры трех остальных ее стоек представляют собой обычные защемления. На рис. 1b изображены ядра описанных конструкций. Ядро конструкции 1 устойчивости при сжатии не теряет, ибо продольные силы в его элементах отсутствуют. Сразу становится ясно, что получить с его помощью какие-либо оценки для нижней критической нагрузки нельзя.

Гораздо опаснее ситуация, возникающая при анализе ядра второй конструкции. Вычисления показывают, что ₃оно теряет устойчивость при q ^я = 25,0823 EI / 1³ . Если принять эту величину в качестве нижней оценки для критической нагрузки и строить решение задачи, постепенно увеличивая ее значение, то обнаружится, что все односторонние связи становятся активными и система потеряет устойчивость при q * = 29,3950 EI / 1 3 . Однако, и это снова показывают вычисления, нагрузка q * критической не является. Таковая гораздо меньше: q _к р = 16,6917 EI / 1³ .

Полученный результат объясняется тем, что среди опорных связей конструкций 1 и 2 имеются так называемые дестабилизирующие связи. При постановке таких связей сопротивляемость конструкции потере устойчивости не повышается, а падает. Дестабилизирующие связи встречаются и в обычных конструкциях, но намного чаще ими обладают системы с односторонними связями. Конструкция 2 теряет устойчивость при q _к р = q ^в = q ^н = 16,6917 EI / 1 ³. Никакой опасности перескока не существует, поскольку при любой величине q отрыва стоек от основания не будет. Функционирует только одна рабочая система, совпадающая с исходной конструкцией.

а)

Ядро конструкции 1

Конструкция 1

Конструкция 2

Ядро конструкции 2

Рис. 1. Примеры конструкций, которые менее устойчивы, чем их ядра

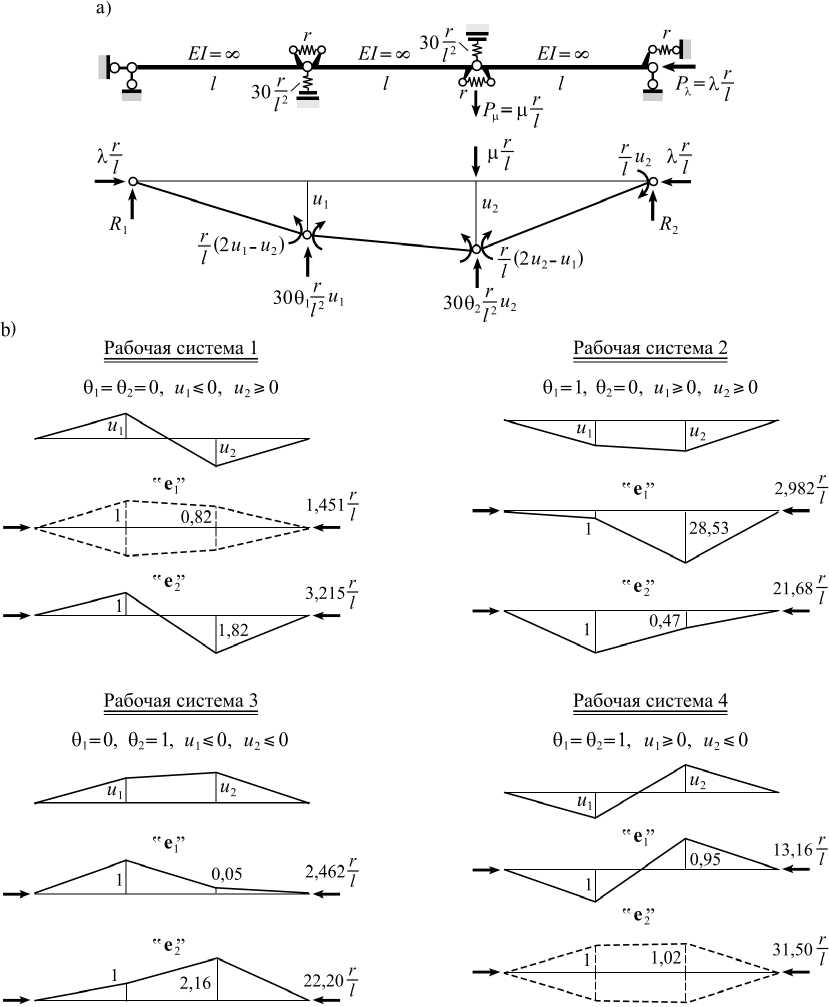
Рис. 2. Конструкция с двумя степенями свободы и ее рабочие системы

Опасаться перескока приходится лишь тогда, когда в ходе наращивания нагрузок P _μ и P _λ при некотором значении λ=λ * происходит переключение односторонних связей еще до того, как начальная рабочая система потеряет устойчивость. Приходится выяснять, имеются ли такие рабочие системы, которые допускают существование собственных векторов при собственных значениях, не превышающих величины λ *. Как показал приведенный выше пример, судить об этом, опираясь на знание критической силы ядра, небезопасно, да и не у всех систем с односторонними связями имеется ядро. В общем случае надежен только один подход: задача на собственные значения должна быть решена для всех рабочих систем конструкции. При большом числе односторонних связей это сделать не удастся, но для иллюстрации того факта, что без полного перебора рабочих систем не обойтись, достаточно рассмотреть пример расчета на устойчивость системы с небольшими числами односторонних связей и степеней свободы.

Изображенная на рис. 2а конструкция состоит из трех абсолютно жестких элементов, связанных между собой упруго податливыми шарнирами, в которых возникает реактивный момент r при взаимном повороте соединяемых элементов на единицу. Эта конструкция с двумя степенями свободы имеет две односторонние связи, способные воспринимать лишь раст2яжение. Жесткость связей равна величине 30r/l2 . На рис. 2 также указаны воздействия Pμ = μr/l, Pλ =λr/l и расчетная схема, отвечающая отклоненному положению равновесия. В качестве параметров состояния приняты узловые перемещения u1 и u2 . Через θi обозначен индекс состояния односторонней связи: θi =1 , если связь с номером i активна, и θi =0, если указанная связь пассивна. Сказанное далее относится к случаю, когда нагрузка Pμ прикладывается не позже того момента времени, как начала действовать сила Pλ .

Прежде всего отыскивается рабочая система, воспринимающая воздействие P _μ при λ= 0, ибо именно она первой включается в процесс деформирования при наращивании параметров μ и λ . При любом μ ≠ 0 этот процесс начинается с отключения правой односторонней связи и включения левой связи, то есть при u ₁ ≥ 0 и u ₂ ≥ 0 . По рис. 2b видно, что таким условиям отвечает рабочая система, получившая номер 2.

На рис. 2b приведены и все остальные рабочие системы вместе с результатами решения задачи на собственные значения. Видно, что оба собственных вектора рабочей системы 2 (как и рабочей системы 3) не противоречат характеру односторонних связей, тогда как в рабочих системах 1 и 4 реализоваться могут только по одному собственному вектору из двух. Рабочая система 2 теряет устойчивость при X = 2,982 и любом ц >  0, в чем можно убедиться, анализируя систему уравнений равновесия, составленную для деформированной схемы конструкции:

(20 9 1 + 2 - X ) и 1 + (10 в ₂ — 2/ 3) и ₂ = Ц l /3, (10 9 1 - 1) и 1 + (20 9 2 + 8/3 - X ) и ₂ = 2 ц l /3.

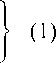
Здесь надо положить 9 1 = 1, 9 2 = 0. Можно также проверить, что с увеличением параметра Хе [0 2,982] односторонние связи не переключаются, а при Хе (2,982 17,5] и Х> 21,685 рабочая система 2 равновесных состояний не имеет (рис. 3).

Итак, критическое состояние конструкции обнаружено, но его статус пока неясен. Требуется выполнить анализ всех остальных рабочих систем. Ядром конструкции является рабочая система 1: обе односторонние связи отключены ( 9 1 =9 2 = 0), и система неизменяема. Выше уже отмечалось, что к первому собственному числу ядра как к нижней оценке критической силы конструкции в целом следует относиться с осторожностью. Но в данном случае это неважно, так как первый собственный вектор рабочей системы 1 нереализуем. Вектору e 2 отвечает собственное значение X = 3,215. Оно превышает найденное ранее критическое значение Х = 2,982 параметра X для рабочей системы 2. Анализ решений уравнений (1) при 9 1 =9 2 = 0 приводит к выводу, что функционирование рабочей системы 1 возможно лишь тогда, когда Хе [2,5 3,215].

Что же касается рабочей системы 3, то односторонние связи не препятствуют реализации обоих собственных векторов, при этом ее первое собственное число Х = 2,462 меньше первого собственного числа рабочей системы 2. Если ц > 0, то рабочая система 3 имеет согласованные с характером односторонних связей перемещения только тогда, когда Х> 22,204. Стало быть, для перескока при 22,204 >Х> 2,462 из равновесного состояния рабочей системы 2 в равновесное состояние рабочей системы 3 требуется дополнительный приток энергии извне. (Такой приток, в частности, может обеспечить и сама сила P , будь она приложена с эксцентриситетом, обусловленным начальными несовершенствами.) Об источнике дополнительной энергии и о ее величине ничего конкретного сказать нельзя, если оставаться на уровне решения линеаризованной задачи устойчивости.

У рабочей системы 4 первое собственное число слишком велико, а потому анализ ее равновесных состояний интереса не представляет. Таким образом, согласно решению линеаризованной задачи,

Х ^н = 2,462; Х ^в = 2,982. (2)

И все же уверенным можно быть только в отношении верхней критической силы, тогда как величину Х н = 2,462 можно рассматривать только в качестве приближенного значения нижней критической силы при совершенно неопределенных шансах ее реализации. В самом деле, при ц Ф 0 собственный вектор, отвечающий собственному числу Х ^н = 2,462, не является равновесным.

Необходимо также обратить внимание на то, что в ходе решения линеаризованной задачи можно проанализировать далеко не все равновесные состояния конструкции.

На рис. 3 жирными горизонтальными линиями выделены интервалы изменения параметра X , на которых рабочие системы 1-4 способны поддерживать состояния равновесия, согласованные с характером односторонних связей. Кружками отмечены собственные значения задач устойчивости рабочих систем. Полые (кольцевые) кружки отвечают реализуемым собственным значениям. Зоны, в которых равновесные состояния отсутствуют («мертвые зоны»), затенены. Речь идет об интервалах 3,125 < X <  13,146 и 21,685 <Х< 22,205. Кроме того, наблюдается неединственность решения: на интервале 2,5 <Х< 2,982 равновесные состояния конструкции поддерживают рабочая система 1 и рабочая система 2. Все это свидетельствует о необходимости обращения к решению нелинеари-зованной задачи.

Рис. 3. Диапазон равновесных состояний рабочих систем по параметру λ при μ > 0

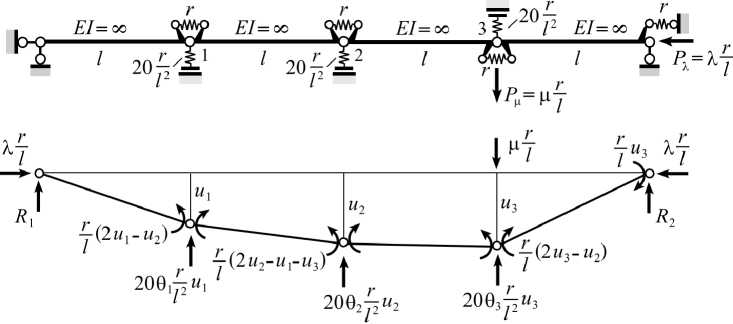
Рис. 4. Система с тремя степенями свободы и тремя односторонними связями

Условия функционирования систем сравнения

Система сравнеНИЯ	Индексы включения связей			Допускаемые знаки перемещений			Собственные значения
	61	02	Оз	U\	^2	W3	X,	Х2	Х3
1	0	0	0	-	-	+	0,924028	2,305658	3,520315
2	0	1	0	—	+	+	2,181729	3,284064	21,284208
3	0	0	1	—	-	—	1,417248	3,189862	17,142891
4	0	1	1	-	+	-	2,422691	10.259547	29,067762
5	1	0	0	+	-	+	1,973569	3,307414	16,469018
6	1	1	0	+	+	+	2,949084	10,056748	28,744169
7	1	0	1	+	-	-	2,946064	12,236662	21,567274
8	1	1	1	+	+	-	9,338002	12,251405	35,160593

Система, изображенная на рис. 4, заимствована из монографии [2]. По сравнению с рассмотренной ранее конструкцией у нее на одну одностороннюю связь больше и на единицу больше число степеней свободы. У новой конструкции имеются 8 подконструкций – систем сравнения, претендующих на роль рабочих систем. В таблице указаны результаты решения задачи на собственные значения для каждой системы сравнения. Собственные числа, которым отвечают собственные векторы, не противоречащие характеру односторонних связей, выделены жирным шрифтом. Видно, что при ц = 0 существуют только три рабочие системы – это системы сравнения 3, 6 и 8, и что устойчивость теряет первая из них: X = 1,417248. Но если ц> 0, то ограничиться кр анализом деформирования только рабочих систем 3, 6 и 8 нельзя, ибо при ц ^ 0 в зависимости от значения параметра X роль рабочей системы может взять на себя любая из систем сравнения.

Анализу подлежат решения системы уравнений равновесия, составленных для деформированной схемы конструкции (рис. 4):

(15 0 1 + 2 -X ) и 1 + (1О 0 ₂ — 1) и 2 + (5 0 ₃ + 1/4) и ₃ = Ц l /4,

(10 0 1 - 1) и 1 + (20 0 2 + 2 -X ) и ₂ + (1О 0 ₃ - 1/2) и ₃ =ц l /2, 1 (3)

5 и 1 + (10 0 2 - 1) и ₂ + (15 0 ₃ + 11/4 - X ) и ₃ = 3 ц l /4.

Результаты анализа представлены на рис. 5, который выполнен в том же духе, что и рис. 3.

Напомним, что рассматриваются только такие истории нагружения, при которых воздействие Р ц прикладывается до того, как хотя бы одна из рабочих систем теряет устойчивость. Тогда первой начнет деформироваться та система сравнения, которая является рабочей системой при нагрузке Р ц и X = 0. В данном случае это рабочая система 2. По рис. 5 видно, что воздействие р воспринимается этой рабочей системой только до тех пор, пока X <  2, тогда как рабочих систем, воспринимающих сжимающую силу при 2 12,25, нет вообще. Это означает, что вопрос о верхней критической силе остается открытым, так как величина X = 2 меньше первого собственного числа рабочей системы 2. Однако если параметр нагружения X принадлежит диапазону [1,417248 2] и возможен приток энергии извне, то существует вероятность перескока из состояния равновесия, поддерживаемого рабочей системой 2, в равновесное состояние рабочей системы 3. Это позволяет рассматривать величину X ^h = 1,4172482 как ориентир для параметра, характеризующего нижнюю критическую силу. Ничего более определенного по результатам решения линеаризованной задачи устойчивости сказать нельзя.

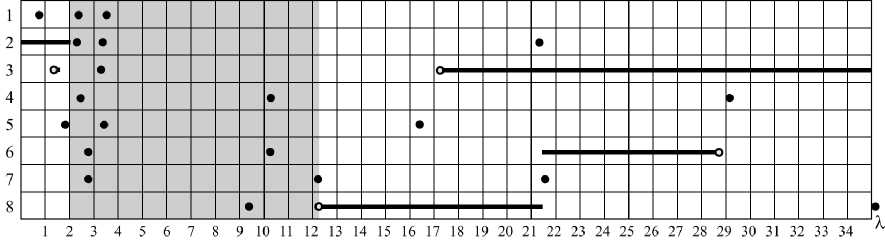
Рис. 5. Диапазон равновесных состояний систем сравнения по параметру λ при μ > 0

Несколько слов о неединственности состояний равновесия конструкции с односторонними связями при наличии воздействий P _λ и P _μ . На рис. 3 и 5 видны интервалы значений параметра λ , на которых одно и то же воздействие может быть воспринято разными рабочими системами. Так (рис. 3), при 2,982 ≤λ≤ 3,125 заданная нагрузка может быть уравновешена реакциями как рабочей системы 1, так и реакциями рабочей системы 2. На рис. 5 имеются две зоны неединственности: при 17,143 ≤λ≤ 21,500 способны функционировать рабочие системы 3 и 8, а при 21,500 ≤ λ ≤ 28,144 – рабочие системы 3 и 6.

Собственно говоря, именно неединственность состояний равновесия конструкции и обеспечивает возможность обсуждаемого перескока. Он может реализоваться двумя способами. О первом из них говорилось при анализе устойчивости конструкции, изображенной на рис. 2. Нижняя критическая сила этой конструкции совпадает с критической силой рабочей системы 3. Однако точка ее реализации при наличии воздействия Pμ является изолированной (рис. 3): она отвечает только состоянию μ =0, λ=2,462 . Поэтому перескок из положения равновесия рабочей системы 2, в которой реализуется верхняя критическая сила, в состояние равновесия рабочей системы 3 возможен лишь при наличии постоянно действующего фактора, способствующего появлению в рабочей системе 3 допустимых положений равновесия. Как было отмечено выше, таким фактором могут быть начальные несовершенства, в частности эксцентриситет осевой силы или начальная погибь. Но этого мало. Нужен еще внешний импульс, обеспечивающий сам пере- скок после того, как были созданы условия для его реализации.

Если же точка бифуркации, отвечающая нижней критической силе, изолированной не является (см. информацию о рабочей системе 3 на рис. 5), то для перескока требуется только дополнительный импульс.

Однако при любом способе своей реализации сам перескок не является свидетельством потери устойчивости конструкции: например, в случае, когда сопряженные по перескоку состояния устойчивы, а принадлежащие им перемещения малы, хотя и различны.

Сказанное иллюстрирует рис. 6. Перескок происходит при некотором λ * ∈ [ λ ^н, λ ^в] из рабочей системы 2 в рабочую систему 1. Соответствующим равновесным состояниям отвечают изображающие точки А и В . Оба состояния устойчивы, первое из них докритическое (рабочая система 2), а второе – послекритическое (рабочая система 1). Если после перескока наращивать осевую силу, то точка В будет смещаться вправо до тех пор (до положения С на рисунке), пока рабочая система 1 обладает равновесными состояниями. А уменьшение параметра λ после перескока действительно может привести к потере устойчивости по достижению изображающей точкой позиции D .

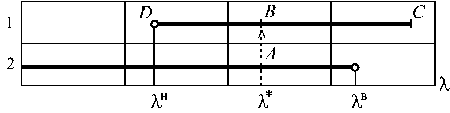
Рис. 6. К неединственности состояний равновесия