Линейно-квадратические дискретно-непрерывные системы с управляемыми коэффициентами

Наряду с традиционными исследованиями в теории оптимального управления наблюдается постоянный интерес к моделям управления системами неоднородной структуры, систематические исследования которых начаты еще в 1960-е–1970-е гг. В различных публикациях эти системы фигурируют под разными названиями: системы переменной структуры [1] , дискретно-непрерывные системы [2] , логико-динамические системы [3, 4] , импульсные системы [5] , гибридные системы [6 , 7] . Однако для подобных систем классические методы оптимального управления непосредственно неприменимы. Один из возможных подходов к исследованию задач оптимального управления для систем неоднородной структуры состоит в обобщении для

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований: проекты 14-31-50894 мол_нр «Разработка и исследование алгоритмов оптимизации линейных динамических систем с управляемыми коэффициентами», 15-01-01923 А «Конструктивные методы оптимизации управления системами неоднородной структуры».

○c Программные системы: теория и приложения, 2015

них достаточных условий оптимальности Кротова [8] . В [9] сформулированы общие условия оптимальности для абстрактной динамической системы как многошаговой, операторы которой на разных шагах допускают различную интерпретацию. В [2 , 10 –12] предложена и развита математическая модель дискретно-непрерывной системы (ДНС) в виде конкретизации указанной абстрактной модели [9] , применимая для широкого класса задач управления неоднородными процессами, и для нее получен аналог достаточных условий Кротова для непрерывных и дискретных систем. Как и в случае однородных систем, получение закона управления в форме синтеза для ДНС при численной реализации вызывает серьезные трудности, связанные с «проклятием размерности». Для преодоления этих сложностей в теории управления принято разделять задачу управления на два больших этапа:

• (1)    поиск оптимальной (либо вообще некоторой желаемой) временной программы управления,

• (2)    построение приближенно оптимального синтеза управления с обратной связью в окрестности этой программы с целью ее реализации на основе упрощенной модели объекта, допускающей аналитическое или близкое к нему достаточно простое решение.

Соответствующее направление, связанное с решением задачи (2), получило интенсивное развитие как теория аналитического конструирования оптимальных регуляторов (АКОР) в работах А.М. Летова [13, 14] , Р. Калмана [15] и в ряде других публикаций, где исходная модель заменяется неким линейно-квадратическим приближением.

В данной работе рассматривается модель линейно-квадратической ДНС как частный случай общей модели [12], и для нее строится аналог метода глобального улучшения управления [12] , позволяющий получить решение в форме приближенно-оптимального синтеза. В отличие от работ [13, 14] предлагается линейно-квадратическое приближение функций Кротова–Беллмана и обобщенного лагранжиана Кротова в окрестности реализуемой программной траектории, как для итерационного поиска оптимальной программы, так и для приближенно-оптимального синтеза в ее окрестности, который автоматически находится по окончании итерационного процесса. Полученный результат можно рассматривать как развитие теории АКОР для ДНС в рамках иного подхода к задачам АКОР, предложенного в [16]. В заключение приведены результаты вычислительных экспе- риментов на методическом примере.

• 1.    Линейно-квадратические дискретно-непрерывные процессы и основные конструкции

Рассматриваемая модель ДНС представляет собой двухуровневую управляемую систему. На верхнем уровне фигурирует дискретная модель

• (1)         x°(k + 1) = x°(k) +— a(k,u)lxl² + b(k, u), x° E R,

• (2)          x(k + 1) = A(k,u)x(k) + B(k,u), x E R ^{m ( k )},

k E K = {kI,kI + 1, ..., kF}, и E U(k, x) C Rr(fc), где k — номер шага (этапа), не обязательно физическое время, U(k,x) — заданное при каждом k и x множество, a(k,u), b(k,u) — заданные функции, A(k,u), B(k,u) — матрицы размеров m(k) х m(k), m(k) х 1 соответственно.

На некотором подмножестве K ‘ C K , k _F E K ’ действует непрерывная система нижнего уровня

• (3)                x ^c0 = -a^c(t, u ^c )|x ^c | ² + b ^c (t, u ^c ), x ^c0 E R,

• (4)              x ^c = A ^c (t,u ^c )x ^c + B ^c (t,u^c), x ^c E R ^{n ( k )} ,

t E T (z) = [ti(z),tF(z)], xc E Xc(z,t) C Rn(fc), uc E Uc (z,t,xc) C Rp(fc), z = (k, x) , ac(t, uc), bc(t, uc) — заданные функции, Ac(t, uc), Bc(t, uc) — матрицы размеров n(k) х n(k), n(k) х 1.

Оператор правой части (1) имеет вид

x(k +1) = y(k)xc(k,tF), k E K‘, xc(tI) = ^(k)x, где через ^, 9 обозначены матрицы соответствующих размеров. Здесь z = (k, x) — совокупность переменных верхнего уровня, играющая на нижнем уровне роль параметров.

Решением этой двухуровневой системы считается набор m = (x(k),u(k)), где при k Е K‘: u(k) = mc(k), mc(k) Е Dc(z(k)), (называемый линейно-квадратическим дискретно-непрерывным процессом), где mc(k) — непрерывный процесс (xc(k,t), uc(k,t)), t Е T(z(k)), а Dc(z) — множество допустимых процессов mc удовлетворяющих указанной дифференциальной системе (3)–(4) при кусочно-непрерывных ис(к,к) и кусочно-гладких хс(к,к) (на каждом дискретном шаге к).

Будем рассматривать для модели (1) – (4) задачу оптимального управления как задачу о минимуме функционала I = х ⁰ (к р ) на множестве D решений т при фиксированных к / = 0, к р , х (к / ) и дополнительных ограничениях х(к) е Х (к).

В общем случае достаточные условия оптимальности для такой задачи получены в [12]. Функции Кротова р, рс зададим в виде р = фт (к)х + -хтсг(к)х — х0, рс = фст(к, t)хc + -хсТсгс(к, t)хc — хс0, где ф(к), фc(k,t) — вектор-функции, а ст(к), стc(k,t) — матрицы соответствующих размеров. При этом основные конструкции общих достаточных условий для рассматриваемой задачи имеют вид:

G = ф ^т (к _р )х + - х ^т а(к _р )х,

R = ф ^т (к + 1)(А(к, и)х(к) + В(к, и)) — х ⁰ (к) —

• —    -а(к, и) |х| 2 — Ь(к, и)+

+ - (А(к, и)х(к) + В(к, и))^Т а(к + 1) (А(к, и)х(к) + В(к, и)) —

• —    ^ ^т (к)х — -х ^т ст(к)х,

G ^c = —ф^т(к + 1)0(к)х ^с (к, t _P ) — - (0(к)х ^с (к, t _P )) ^т ст(к)0(к)х ^с (к, t _P )+

+ ^ ^т (к)х + -х ^т ст(к)х + ф ^{с т} (к _р )х ^с (к, t _P ) — ^ ^ст (к / )^(к)х+

+ -х ^ст (k,t _р )а ^с (k,t _р )х ^c (k,t _р ) — -(^(к)х) ^т ст ^с (к, t / )^(к)х,

R ^c = х^сТ(ф ^с + ^ ^с (к, t))(А ^c (t, и ^с )х ^с + В ^c (t, и ^с )) —

• — -a^c (t, и ^с )|х ^с | 2 — b ^c (t, и ^с ) + -ф ^{с т} х ^с + -х ^{с т}гг ^с (к, t)х ^c ,

  
  
  

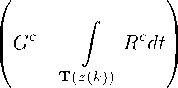
• 2. Метод глобального улучшения

^L = ^{G —} ^ ^R + ^

K \ K ‘ \ k _F       K ’

Здесь L — обобщенный лагранжиан, который на множестве D , как показано в [12] , совпадает с исходным функционалом I . В соответствии с общей процедурой [12] решение поставленной задачи сводится к исследованию на экстремум введенных конструкций по указанным аргументам при каждом к, t.

В работах [17 , 18] был предложен метод глобального улучшения управления, его аналог для ДНС получен в работе [12] , а модификации для линейных ДНС и билинейного случая в [19, 20] . Для однородных процессов один из возможных подходов к реализации указанного метода дан в [21] . Рассмотрим далее его модификацию для класса линейно-квадратических ДНС (1) – (4) , но предварительно укажем исходные предпосылки.

Предположим, что X (k) = R ^m(fc) , X ^c (z,t) = R ^n(fc) , t _I = т (z), t p = ”d(z), k _I , x i и k _p — заданы, x ^c _p E R ^n(fc) .

Задан элемент m ¹ E D и требуется найти элемент m ¹¹ E D такой, что I (m¹¹) <  I (m¹) . Функции p (k, x (k)) , p ^c (z, t, x^c) найдем из условий:

R (k, x(k'),u^I(k)^ ^ min, G (x) ^ max,

R ^c (z, t, x ^c (k, t) , u ^c (k, t)) ^ min, ^v                                  '        X^е

G^c (z,x^c(t p ,z)) - I

T ( _Z )

R ^c (z(k), t, x ^c (t, z), u ^cI (k, t))dt ^ max,

X

где x^c(t, z) — результат операции в (7) . Минимизация и максимизация производится по областям, где ожидается прохождение улучшенной траектории. Такие области, как правило, известны в практических приложениях.

Эти условия могут быть выполнены неоднозначно и оставляют значительную свободу выбора функций p и pc. Если потребовать, чтобы левые части в этих условиях не зависели от x, xc, то получится дискретно-непрерывная цепочка относительно p, рс, описываемая уравнениями типа Беллмана, не содержащими операции поиска максимума по и, ис и, следовательно, линейными относительно ус:

• (9)      у (к,х) = у (к + 1,/ (к, х (к) , и ¹ (к))) , к Е К \ К ‘ \к _Р ,

• (10)         у (к р , х) = —F (х) , ) ^с = —Н ^с (z,t,x^c,у^ _K c ) ,

Н ^с (z, t, х ^с , и^с\р) = р ^т / ^с (z, t, х ^с , и ^а ) ,

• (11)               ) ^с (z,t _F ,х р ) = у (к + 1,в (z,x p )) ,

• (12)              у (к,х) = ) ^с (z,T (z) ,^ (z)) , к Е К ’ ,

которая разрешается в порядке следования от к р к к ; .

Пусть

U (к, х) = arg max R (к,х (к) , и (к)) , u ^ U ( k,x )

и ^с (z,t,х ^с )= arg    max    R ^с (z,t,х ^с ,и ^с ) .

u ^c e u ^c ( z,t,x ^c )

Тогда из заданной дискретно-непрерывной системы и начальных условий при полученных управлениях находятся функции X II (к), х ^сII (к,t) и программы управлений:

и11 (к) = U (к, XII(к)) , I (к, t) = Кс (к, t, хп(к), хс11(к, t)) , т.е. элемент mII. Повторяя итерационно эти операции, получим улучшающую последовательность {ms}.

Теорема 1. Для элементов m I и m II справедливо неравенство I (m I ) >  I (m II ) .

Доказательство. Покажем, что I (m II ) — I (m I ) < 0. Имеем

I (m II ) — I (m I ) = L (m II , ) I , ) ^с1 ) — L (m I , ) I , ) ^с1 ) =

= G (x ¹¹, ) ¹ ) —G (x ¹ ,) ¹ ) — ^ (R (к, X II (к), и ¹¹ (к), ) I ) —

K \ K ‘ \ k _F

• —    R (к, x I (к), и ¹ (к), у ¹ )) + ^ (G ^с (z II (к), ) I , ) ^с1 ) —

K ^′

• —    G ^с (z I (к), у ¹ , у ^с1 )) — У (R ^с (z ^II (к),t, x ^сII (t), и ^сII (t), у ¹ , у ^с1 ) —

T ( _Z )

• —    R ^с (z ^I (к), t,x ^сI (t), и ^сI (t), у ¹ , у ^с1 )) dt = A i — Д 2 + Д 3 — Д 4 .

где Д 1 = G (х ¹¹) — G (х¹) < 0 в силу условия (6) .

При этом

Д 2 =           ( R (к, ж ¹¹ (к) , _М^п (к) , y I ) — R (к, ж ¹ (к) , и ¹ (к) , у ¹ )) =

K \ K ‘ \ k _F

= Е ( R (к, ж ¹¹ (к) ,и^п (к) , y I ) — R (к, ж ¹¹ (к) ,u I (к) ,y I )) + K \ K ‘ \ k _F

+    ^^    (R (к, ж ¹¹ (к) , и ¹ (к) , у ¹ ) — R (к, ж ¹ (к) , и ¹ (к) , у ¹ )) > 0

K\K‘\kF согласно (5).

Далее имеем

Д з = E (° ^C (^Z II (к) , У ¹ , y ^CI ) — ^{G C} (^Z I (к), У ¹ , y ^CI )) < 0 K ^′

и

Д 4 = У (R ^c (z II (к) , t, ж I (t), u ^cII (t), у ¹ , y ^cI )

T ( _Z )

—R ^c (^(к), t, ж ^{с 1} (t), u ^{c I} (t), y I , y ^{c I} )) dt =

= I (R^C ( ^Z II (к), t, ж ^с11 (t), u ^cII (t), y I , y ^cI ) T ( _Z )

—R ^C ( z ⁱⁱ ( / ) , t, ж ^cII (t), u ^CI (t), y I , y ^CI )) dt+

+ I (R ^C (^{z II} (.к),t,ж ^{c II} (t),u ^{c I} (t),y^I,y ^{c I} ) —

T ( _Z )

—R ^C (г ¹ (к), t, ж ^cI (t), u ^CI (t), y I , y ^CI )) dt > 0

в силу условий (7) , (8) . Тогда

I (mⁿ) — I (m I ) = Д 1 — Д 2 + Д ₃ — Д 4 < 0.

□

Вернемся к исходной задаче и рассмотрим соотношения (9) – (12)

более подробно. Из указанных равенств получаем:

• (13)                      '(к р ) = 0, о(к р ) = 0,

• (14)     '(к) = А^т(к, u ^I )'ф(k + 1) + А^т(к, u I )ст(к + 1)В(к, u I ),

• (15)    о(к) = А ^т (к, п¹)^(к + 1)A(k,u ^I ) — а(к,и¹')Е, к Е К \ К ‘ \к р ,

• (16)                 ' ^c = A^cT(t, u^cl)' ^c + o^cB ^c (t, u ^cI ),

• (17)                  о ^c = —a ^c (t, u^cl)E + CT ^c A ^{c T} (t, u ^cI ),

• (18)          ' ^c (k,t p ) = 6 ^т (к)'(к), A'A-Jp ) = в ^т а(к)в,

• (19)     '(к) = ( ^T ' ^c (k +1,t j ), о(к) = (^(к +1,t _t )( к Е К ’ .

Замечание 1. Если уравнения (1) , (3) содержат линейные слагаемые:

х°(к + 1) = х ⁰ (к) + а°(к, u)x + — a(k, u)|x| 2 + Ь(к, и),

X ^{c 0} =a^c0(t,u ^c )x ^c + |a ^c (t,u ^c )|x ^c | 2 + b ^c (t,u ^c ), где a ⁰ (k,u), a ^{c 0} (t,u ^c ) — вектор-функции строки, то уравнения для ', ' ^c примут вид:

'(к) = —Ea ^0T + А ^т (к, u ^I )'(k + 1) + А ^т (к, u ^I )ст(k + 1)В(к, u I ), ' ^c = —Ea ^c0T + A ^cT (t, u ^cI )' ^c + B ^cT (t, u ^cI )j ^c .

Нетрудно видеть, что выражения для поиска функций U,U ^c пополнятся дополнительными слагаемыми.

Таким образом, алгоритм метода состоит из следующих этапов:

• 1.    Задается элемент т ¹ .

• 2.    Справа налево решаются системы уравнений (13) – (19) относительно вектор-функций ', ' ^c и матриц о, о^с.

• 3.    Находятся функции U, U ^c из условий

U (к,х) = arg max ('(к + 1)^T)B(k,u) — b(k,u)+ u e u ( fc,x )

• + - (А(к)х(к) + В ( к, u)) ^T о ( к + 1)(А(к)х(к) + В ( к, u)), U ^c ( z,t, x ^c ) = arg max      f (' ^c (k, t) + о ^c (k, t)x ^c ) ^T B ^c (t, u ^c ) — b ^c ( t, u ^c ) ) .

• 4.    Полученные управления подставляются в исходную ДНС. Тем самым находится элемент m ¹¹ .

u = E U = ( z,t,i = ) V                                                       /

Подчеркнем тот факт, что управления й, й ^с зависят от переменных состояний верхнего и нижнего уровней линейно-квадратическим образом, т.е. дают решение в форме приближенного синтеза оптимального управления. Такую форму решения можно рассматривать как один из видов АКОР для ДНС. При этом, в отличие от традиционной задачи АКОР, которая получается при линейно-квадратической аппроксимации исходной нелинейной задачи по состоянию и управлению, здесь рассматривается аппроксимация только по состоянию, а управление остается нелинейным, ограниченным исходным множеством, что позволяет использовать имеющиеся ресурсы управления полностью.

Процесс итераций заканчивается при выполнении условия

^s+l — Is | < е, где е — заданная точность вычислений.

Заметим, что если функционал ограничен снизу, то построенный итерационный процесс сходится по функционалу. Действительно, в силу теоремы 1 алгоритм генерирует монотонную по функционалу улучшающую последовательность, которой соответствует монотонно убывающая числовая последовательность I _s = I(m _s ), сходящаяся, как известно из анализа, к некоторому пределу I * .

Пример 1. Рассматривается нелинейная задача:

х1 = (х2 )2(х2 — 1)2 + (t — 1)х2 + Х2й,   X2 = й, х1(0)=0, х2 (0) = 0,

|й| < 2,   0 <  t < 2, I = х ¹ (t _p ) ^ inf,    t _p = 2.

Эта задача при предположении, что управление не ограничено, сводится к производной задаче (первого порядка) [22 –24] :

у = х ^{1 -} 2 ⁽ х 2 ⁾ 2 ,

^ inf,

у = (х ² ) ² (х ² — 1) 2 + (t — 1)х ² ,

I = (« г + 2(х Р ) ² )

которая решается непосредственно минимизацией правой части и функционала по новому управлению. Нетрудно видеть, что правая часть указанного уравнения — выпуклая функция по переменной х ² и, следовательно, ее минимум достигается в стационарной точке.

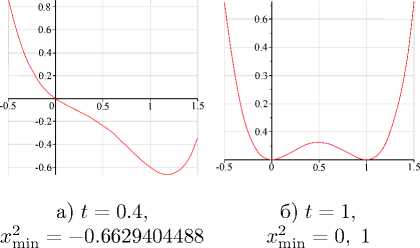
Рис. 1. Графики х ² для некоторых t

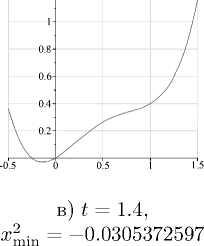
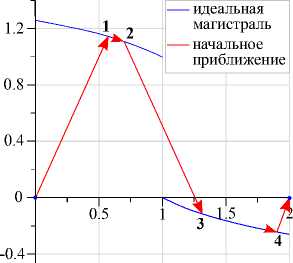
Рис. 2. Идеальная магистраль и начальное приближение

Для его поиска при фиксированном t с некоторым шагом на отрезке [0, 2] находился минимум функции (ж ² ) ² (ж ² — 1) 2 + (t — 1)ж ² . На рис. 1 представлены графики ж ² для некоторых значений t. Непосредственно из выражения функционала следует, что его минимум достигается на управлении ж ^ = 0. Тем самым получается идеальное магистральное решение исходной задачи с кусочно-непрерывной функцией ж ² (t) в качестве управления. Это решение модифицируется естественным образом — заменой в окрестностях точек разрыва решениями уравнения ж ² = к при |к| < 2. Получается кусочно-гладкая функция ж ² (t), используемая далее как начальное приближение в итерационной процедуре минимизации функционала (рис. 2) .

Производится тейлоровская линейно-квадратическая аппрокси- мация исходной системы по х"2 в окрестности траектории текущей s-й итерации:

• (21)    х ¹ = a(t) + b(t)(x ² — x 2 (t)) + -c(t)(x ² — x 2 (t))' 2 + х ² ^ х ² = u,

x ¹ (0) = 0, х ² (0) = х 0 , |u| < 1, 0 <  t < 2,

^a(t) = ^(x 2 ^{) 2 (x} 2 - ^{1) 2} + ^(t - ^1)x 2 ,

b(t) = 2x 2 (x ² — 1)(2x 2 — 1) + t — 1, ^c(t) = ^2((2x 2 ^{— 1) 2 + 2x} 2 ^(x 2 ^— 1)).

Преобразованная система допускает аналогично исходной нелинейной переход к производной системе с использованием того же преобразования у = х ¹ — 2 (x ² ) ² :

• ^{(22)         у} = ^{a(t) + b(t)(x} 2 ^— ^to) ⁺ 2 ^{c ( t )( x} 2 — ^x 2 ^{( t ))} 2 .

Если присоединить уравнение x ² = u, то получится удобная запись системы (21) в новых переменных (у, х ² ), где управление входит лишь в одно уравнение.

Для последовательного улучшения приближенного магистрального решения представим его как дискретно-непрерывный процесс, предполагая, что его структура по итерациям не меняется. Будем рассматривать t _p (к) как дискретное управление u ¹ . В данном случае K ‘ = K \k p = 0,..., 4. Векторы переменных верхнего (дискретного) уровня обозначим через х, u, а нижнего (непрерывного) уровня — через х ^с , u ^c . Будем иметь:

х 1 (к +1)= u ¹ , х 1 (к) <  u ¹ <  u 1max , к Е K ‘ , U max = 2, х 1 (0) = 0.

При к = 2, 4:

Qi = х2(к), х/2 = х3(к), qc = b(t)(:Ec2 — x22(t)) + 2c(t)(xC2 — x22(t))2, хс2 = uc, t Е [х1 (к), u1 (к)], х2(к + 1) = qcF(к), х3(к +1) = хр2(к), |uc| < 2.

При к = 1, 3:

q j = х ² (к), t Е [х ¹ (к), к 1 (к)], q^c = b(t)(х ^е2 - х ^е (к, t)) + 2c(t)(х ^е2 - x = 2 (t)) 2 , х 2 (к + 1) = q ^c _F (к) - 2 (х > ² (к)) 2 , х ³ (к + 1) = к ² (к), b(t) = 2х 2 (х 2 - 1)(2ж 2 - 1) + t - 1, ^c(t) = ^2((2ж 2 ^{- 1) 2 +} 2ж ^{2 (} х 2 ^- 1)).

Переменная х ^е1 (к, t) находится по формуле х ^е1 = q ^c + а + х ^е2 - u _s , a(t) = (X g ² ) ² (X g ² -1) 2 + (t- 1)х ^ ² . Здесь переменная q ^c введена с целью преобразования линеаризованной модели к виду, рассмотренному в теории.

Заданы начальные условия и минимизируемый функционал: х 1 (0) = 0, х ² (0) = 0, х ³ (0) = х ³ , I = х ² (5).

Обратим внимание, что на разных этапах используются разные непрерывные системы: на четных этапах — исходная преобразованная система, а на нечетных — производная.

Соответствующая ДНС для сопряженных переменных ф, ф ^е , ст, ст ^е имеет следующий вид.

При к = 2, 4: ф(5) = 0, ст(5) = 0, ф = (ф ¹ , ф ² , ф ³ ), ф ^е = (ф ^е1 , ф ^е2 ), ст, ст ^е — матрицы размера 3 х 3, 2 х 2, ^ = (0,1,1),

^(к) = ^ф ^е (к + 1, t j ), ст(к) = < ^т ст ^е (к + 1, t j )£, ^) ^е = Е (0, -Ь) + ст ^е (0,1) T , <ст ^е = -cE,

010        010

Ф ^{( к,t} F )= 0 0 1 ^ ^(к) , ^{ст ( к,t} F )= 0 0 1 ^ст(к)

При к = 1, 3:

тф ^е = -b, ст ^е = -с, ф ^е (к,t F ) = ф ² (к), ст ^е (к,t F ) = ст ²² (к), Ф(к) = ^ф ^е (к +1,t j ), ст(к) = ^ ^Т ст ^е (к +1,t j )^, ^ = (0,1,0).

Здесь ст ²² — элемент матрицы ст.

Управляющие воздействия находятся по приведенным ниже формулам.

Таблица 1. Изменение функционала по итерациям

№ итерации	Значение функционала
0	-0.285436
1	-0.296333
2	-0.300289
3	-0.300284

При к = 2, 4:

й ¹ (к, х) = argmax(-^ 1 (к + 1)й 1 +

+ |(й1^ ^с (к),х ^с р)ст (к + 1)(й 1 , q ^c _F (к), х ^ 2 ) ^т , й ^с (z, t, х ^с ) = argmax(^ ^c + а^с(q ^c , х ^с2 )) ^т (^c, й^с)^т(ф^с+

+ ^c(qc,xc2)),   |йс|< 2, где qc = b(t)(xc2 — хс2(к, t)) + 2c(t)(xc2 — xC2(t))2.

При к = 1, 3:

й ¹ (к,х) = argmax(^1^ + 1)й 1 + |(й 1 , q^c_F(к) —

• —    |(х' р ² (к)) ² ,й²)а(к +1')(й¹,q ^c _F (к) — |(х' р ² (к)) ² ,й ² ) ^т ), й ² (к,х) = argmax(^ ³ (k + 1)й ² + -(й ¹ , q _F (к) —

• —    2(х р (к))²,й ² )ст(к +1)(й ¹ ,q ^c _F (к) — |(х' р ² (к)) ² , й ² ) ^т ),

й ^с (z, t, х ^с ) = х ^с2 = argmax(—b(t)(x ^c2 — x C ² (t)) —

• ^—    2 c ^(t)( x ^{c2 —} x C ^{2 (t)) 2 )} .

• 3.    Заключение

Расчеты проводились предложенным в работе алгоритмом. В качестве начального приближения использовалась траектория, приведенная на рис. 2 . Решение получено за 3 итерации. Соответствующие управления и траектория x ² (t) приведены на рис. 3, 4 . Изменение функционала по итерациям дано в таблице 1.

Для сравнения эта же задача в исходной постановке без преобразования к ДНС и специального выбора начального приближения была решена тем же методом при начальном приближении управления й(t) = 0 на всем заданном отрезке времени. Близкое решение

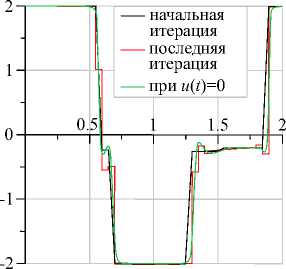
Рис. 3. Управление на начальном приближении и на итерациях

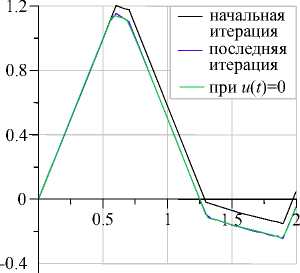
Рис. 4. Траектория ж2 на начальном приближении и на итерациях со значением функционала I = -0.302669 получено за 85 итераций. Траектория и управление также приведены на рис. 3, 4 и носят аналогичный характер.

Таким образом, в работе предложена математическая модель линейно-квадратической по состоянию ДНС с управляемыми коэффициентами, для которой дана конкретизация общих достаточных условий оптимальности и построен метод глобального улучшения управления с линейно-квадратическими функциями Кротова. Доказана теорема об улучшаемости начального приближения.

Этот метод особенно эффективен для вырожденных задач оптимального управления с магистральными решениями, широко распространенных на практике. Это подтверждается проведенными вычислительными экспериментами на тестовом примере. Найденное начальное приближение в магистральной форме дало значительный эффект по сравнению с традиционным случайным выбором начального приближения из множества допустимых управлений.