Линейно-логический алгоритм принятия решения при обработке сигналов

Введение. Для оптимизации обработки сигналов в условиях значительной априорной неопределенности используют процедуры эвристического, инженерного синтеза непараметрических решающих правил. Такая процедура основывается на анализе параметров выбросов случайных процессов на выходе демодулятора приемника дискретных

Машиностроение и машиноведение

сигналов [1–7]. Теория выбросов широко используется в инженерной практике. Однако анализ закономерностей и детальных характеристик выбросов — сложная аналитическая задача даже при постоянном или медленно меняющемся пороге. При аналитическом подходе получаются соотношения, приводящие к несходящимся рядам, и этим объясняется отсутствие физически значимых результатов.

В настоящее время и в ближайшем будущем перспективно применение дискретных многопозиционных сигналов. Это и дискретные адресные системы, и системы многократной телеграфии (частотная телеграфия, многопозиционная частотная телеграфия), и системы с D и Е кодами, в которых последовательно-параллельно во времени передаются элементарные посылки длительностью Т _с на одной или разных частотах [5, 8–10].

При приеме бинарных сигналов на входе решающего устройства присутствуют два случайных процесса, и процедура принятия решения сводится к задаче статистической проверки гипотез. Необходимо определить, какой случайный процесс (из сравниваемых) обладает большей энергией на интервале наблюдения. Процедура принятия такого решения может быть сведена к сравнению величины разностного сигнала на выходе приемника с постоянным нулевым порогом. Таким образом, необходимо сравнивать минимум два случайных процесса (в лучшем случае анализируется случайный процесс с выхода приемника дискретных сигналов при медленно меняющемся пороге).

Статистическая проверка гипотез сводится к анализу взаимных превышений двух и более процессов. Аналитическое представление данной задачи бывает громоздко и не дает инженерных решений [1, 11–15]. Эвристический синтез и статистическое моделирование на ЭВМ позволяют получить значимые инженерные приложения.

При приеме многопозиционных сигналов можно упрощенно представить:

— их спектры S ( f );

— амплитудно-частотные характеристики (АЧХ) фильтров приемников K ( f ) (рис. 1).

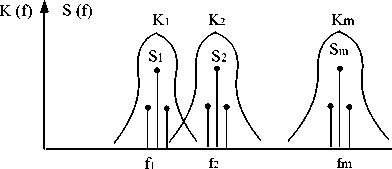
Рис. 1. АЧХ фильтров приемников

Для линейного приемника многопозиционных сигналов обязательно наличие:

— общего усилителя промежуточной частоты (УПЧ),

— общей схемы принятия решения (СПР).

Необходимы также наборы разделительных фильтров (см. рис. 1) и амплитудных детекторов (АД).

Анализ таких приемников показывает [1]: чем больше число позиций сигнала m , тем ниже их помехоустойчивость. Требования к АЧХ фильтров (см. рис. 1) достаточно жесткие. АЧХ не должны перекрываться для обеспечения частотной ортогональности. При этом шумы на выходах фильтров будут независимы. Не должно быть областей перекрытия между АЧХ фильтров, настроенных на частоты f i , (см. рис. 1). Форма АЧХ должна иметь плоский участок в окрестности частоты настройки, чтобы спектры сигналов не искажались.

Следует отметить имеющиеся противоречия. Так, узкополосные фильтры ограничивают скорость работы. При замираниях сигналов и эффекте Доплера возможно ухудшение качества и даже срыв связи. Широкополосные фильтры приводят к взаимопроникновению сигналов соседних по частоте каналов, т. е. нарушается ортогональность и, соответственно, падает качество приема.

Для процессов на выходах фильтров соседних каналов в системах приема и обработки сигналов характерны статистические взаимосвязи, которые увеличиваются при увеличении взаимных перекрытий спектров сигналов либо АЧХ фильтров. Детальное рассмотрение процедуры разделения сигналов по частотному признаку показывает, что при обработке многопозиционных сигналов в случае перекрывающихся АЧХ фильтров можно говорить о попарно зависимых процессах в соседних по частоте каналах. Это имеет особое значение при использовании для оптимизации приема многопозиционных сигналов нелинейных либо линейно-логических процедур [1, 11–14].

Постановка задачи. В условиях значительной априорной неопределенности частота сигналов известна с ограниченной точностью, а диапазон варьирования длительностей элементарного символа может изменяться до тысячи раз. Дополнительное требование: работа в реальном масштабе времени. Ограничимся для простоты случаем обработки бинарных сигналов.

Синтез алгоритма принятия решения. В работах [1, 11-13] рассматриваются особенности обработки дискретных сигналов в условиях значительной априорной неопределенности информации о длительности символа. Задачу можно решить линейными процедурами путем параллелизма алгоритма принятия решения. Проблема усложняется при повышении требуемой точности и расширении диапазона изменения длительностей элементарного символа.

В таких условиях применение адаптивных процедур требует значительного времени на адаптацию или практически нереализуемо из-за высокой априорной неопределенности. Проанализируем возможности эвристического синтеза алгоритма, основанного на учете статистических свойств взаимных превышений двух и более случайных процессов [1, 11-12].

Рассмотрим широкополосный прием с интегрированием или фильтрацией после детектора, когда

А/пT>> 1 (Д/п — полоса пропускания приемника, Т — длительность элементарного символа). В этом случае от- счеты процесса на выходе решающего устройства можно считать распределенными по закону, близкому к нор- мальному. Математическое ожидание и дисперсия этого процесса определяются соотношениями [4]:

NMV x ] = M[ x 1 ] — Mx ₂],          D [ x ] = D [ x 1 ] + D [ x ₂].

Вероятность ошибочного приема рассчитывают по формуле [1-3, 12]:

P = 2[1 - Ф( а )].

Здесь Ф( а ) = ^2 j exp (

-

x ²

—) dx — функция Крампа; а =

Δ M

h

DD   2 + 2 А fT / h h

„ 2

— отношение постоянной со-

ставляющей к эффективному значению переменной; h ² = a-^ — отношение энергии элемента сигнала к спектральной плотности помехи, где а — нормированная амплитуда сигнала, v² — спектральная плотность помехи.

При обработке дискретных сигналов в указанных условиях возможно применение только непараметри-

ческих алгоритмов принятия решения. Сами по себе интересны статистические характеристики выбросов случайных процессов: длительность выбросов (превышений) tп, длительность интервалов между выбросами ТИ, значения максимумов выбросов ^m и т. д. [3]. Алгоритмы оптимизации принятия решения могут быть основаны на учете одной из детальных характеристик, например: число пересечений порога за время наблюдения, длительность интервалов превышения порога и т. д. Необходимо определить информативные признаки таких детальных характеристик взаимных превышений случайных процессов. Технически реализуемый инженерный учет этих данных позволит оптимизировать алгоритм приема и обработки сигналов в указанных условиях.

С энергетической точки зрения наибольшую точность в условиях значительной априорной неопределенности обеспечит учет площадей взаимных превышений S _п (в пределе энергий). Однако это сложно реализовать в реальном масштабе времени алгоритмически и тем более технически.

Понятие выбросов является частным случаем понятия взаимных превышений для двух и более процессов, в том числе случайных. При обработке бинарных сигналов ставится задача анализа выбросов разностного процесса относительно нулевого порога. Она адекватна задаче анализа взаимных превышений огибающих двух процессов в каналах обработки сигналов [3, 11].

Для оптимизации задачи принятия решения в реальном масштабе времени целесообразно учитывать одновременно две и более детальные характеристики выбросов — например, длительность и величину превышения. Произведение длительности на уровень (амплитуда) превышения является оценкой площади превышения (с учетом коэффициента формы превышения) [11].

Воспользуемся двумя детальными характеристиками.

• 1.    Относительный уровень превышения q :

• 2.    Относительная длительность превышений 0 :

q = X, ( t ) / X j ( t ), где Xi ( t ) и X j ( t ) — анализируемые процессы.

• 0 = t _п / т _К , где т _К — интервал корреляции процессов на выходе линейной части приемника, определяемый его полосой пропускания.

Совместный учет указанных характеристик технически сравнительно не труден. При этом его достоверность близка к показателям, получаемым при учете площадей превышений S _п . Учитывая значение термина «превышение», q должно быть больше 1, поэтому в бинарной ситуации при формировании двухпараметрических распределений q определяется соотношением [11]:

Машиностроение и машиноведение

• X , ( t )

• -1     ;       x i⁽ t ) >  x 2⁽ t );

  q = <

  
  

x 2⁽ t )

(i)

X-, ( t )

• -   ;      x 2⁽ t ) >  x i⁽ t ).

x i⁽ t )

Такой подход позволяет анализировать и многопараметрические распределения взаимных превышений двух и более случайных процессов.

Для повышения качества принятия решения необходимо сократить общее количество взаимных превышений процессов. Это следует из результатов анализа двумерных законов распределения взаимных превышений огибающей смеси сигнала и шума и огибающей шума [11]. Необходимо преобразовать процессы таким образом, чтобы, не нарушая отношения правдоподобия, получить формы двумерных распределений, легко различаемые решающим устройством [i2].

Обе задачи решаются применением модифицированного алгоритма комбинированного сложения [1, 11, 14]:

X 1п ( t ) = [ X , ( t ) - KX 2п ( t )] 1[ X , ( t ) - KX , ( t )],

X2П (t) = [X2(t) - KX1п(t)] 1[X>(t) - KX1 (t)], где K — коэффициент, принимающий значения от 0 до 1; 1[Z(t)] — единичная ступенчатая функция, причем 1[Z(t)] = 1 при Z(t) > 0 и 1[Z(t)] = 0 при Z(t) < 0.

Спектры процессов X ш ( t ) и X _2П ( t ), сформированных после обработки по алгоритму (2), расширяются. Их необходимо ограничивать до ширины спектров исходных информационных процессов X ₁( t ) и X ₂( t ).

Значение K определяет реализуемые модификации алгоритма и устройств комбинированного сложения. Речь идет об алгоритме взаимного преобразования, методе комбинированного сложения, системе перекрестного запирания [1, 11].

При K = 1 из детальных характеристик превышений учитывается только факт превышений процессов . Реализуется алгоритм автовыбора при разнесенном приеме сигналов [4] и взаимное преобразование при принятии решения [11].

При K = 0,414 учитываются и факт превышения одного процесса другим, и уровень превышения q [4]. Реализуется комбинированное сложение в разнесенном приеме. При 1 >  K > 0 учитывается не только факт превышения, но и уровень превышения q . Реализуется модифицированный метод комбинированного сложения при принятии решения.

Линейно-логические процедуры, реализуемые в результате эвристического синтеза, позволяют статистически преобразовать исходные случайные процессы. При K = 1 в (2) реализуется автовыбор процессов во времени. Непрерывные во времени процессы (рис. 2, а ) превращаются в последовательности импульсов со случайными амплитудами X ^V t ) и X^t ) (рис. 2, б и 2, в ).

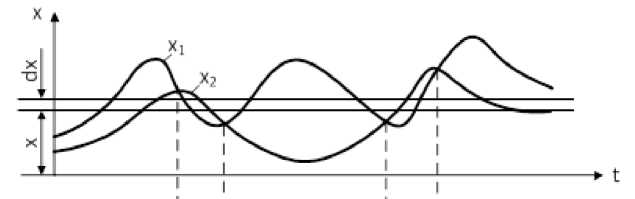
а )

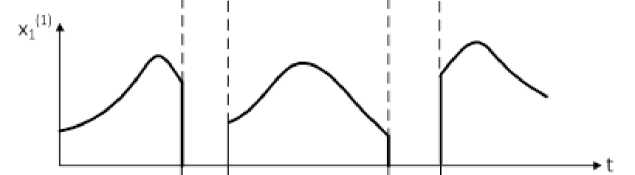
б )

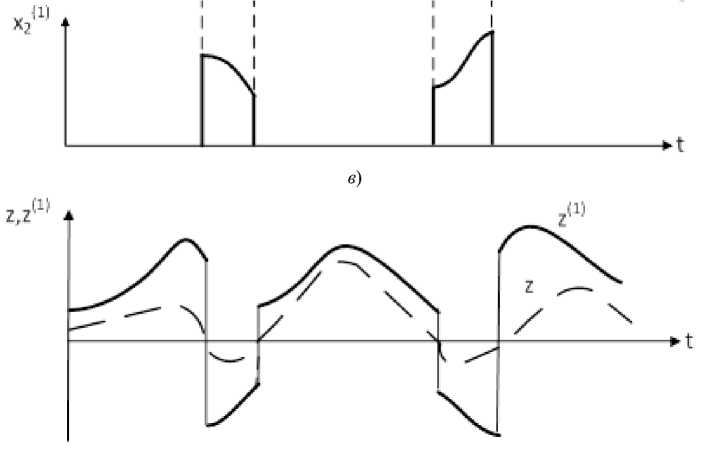
г )

Рис. 2. Комбинированное сложение при K = 1

На рис. 2, г представлены разностные процессы Z = X । - X 2 без обработки и Z ⁽¹⁾ = x 1 ⁽¹⁾ - x ₂⁽¹⁾ после обработки по правилу (2).

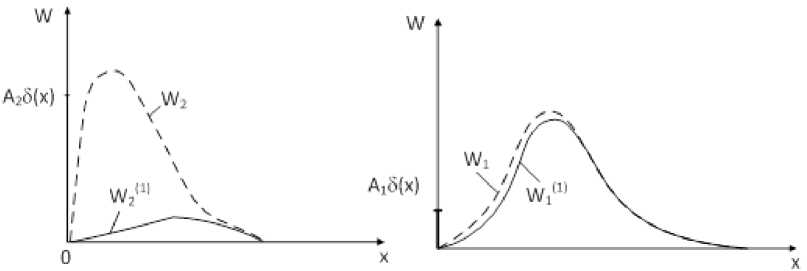
Плотности распределения вероятностей процессов X 1 ⁽¹⁾ ( t ) и X 21) ( t ):

W( (x) = A18(x) + W (x)F2 (x)(3)

W2(1)(x) = A25(x) + W2(x)F1(x).(4)

Коэффициенты A1 и A2 определяются из условия нормировки: fw ,0 W1(x)F2(x)dx,(5)

A = 1 - “ W2 (x)F (x)dx,(6)

где F ( x ) и F ₂ ( x ) — интегральные функции распределения.

Из рассмотрения рис. 2, а — 2, в следует, что часть времени процессы X 1'4 t ) и X 21) ( t ) равны нулю. Поэтому их плотности распределения вероятностей W ⁽¹⁾ ( x ) и W ₂ ⁽¹⁾ ( x ) будут содержать дельта-функции — 5 ( x ) (рис. 3).

а )

б )

Рис. 3. Плотности распределения вероятностей процессов

На рис. 4 представлены плотности распределения вероятностей разностных процессов без обработки по правилу (2) W ( z ) (рис. 4, а ) и после обработки W ⁰⁾( Z ) (рис. 4, б ). Здесь А — зона стирания решающего устройства.

Машиностроение и машиноведение

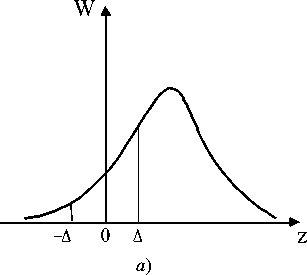
Рис. 4. Плотности распределения вероятностей процессов Z ( t ), Z (1) ( t )

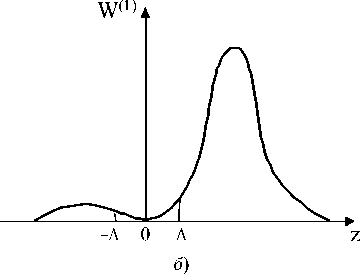
В соответствии с рис. 2, б и 2, в процессы после обработки по правилу (2) — импульсные. Их спектры будут шире спектров исходных процессов. Таким образом, обработка по правилу (2) не приведет к повышению качества приема, а только улучшит пороговые свойства [11–12, 16].

Полная процедура обработки включает две операции:

— линейно-логическую по правилу (2) (она нелинейна по сути, так как в спектре появляются составляющие, которых не было на входе);

— фильтрацию.

Фильтрация учитывает второй параметр превышений Θ — относительную длительность. Расширившиеся спектры процессов остаются в границах, задаваемых при формировании исходных процессов X 1 ( t ) и X ₂( t ) (см. рис. 2, а ).

Обработка по правилу (2) в зависимости от диапазона изменения длительностей ожидаемых сигналов и условий приема [12] может повторяться. При этом значения параметра K различны, всегда меньше 1 и увеличиваются в последующих циклах обработки.

Задачи автоподстройки частоты решаются более эффективно при использовании устройств, реализующих линейно-логическую обработку [14, 17–18]. Сравнительно несложными техническими средствами расширяются полосы захвата и удержания. Обеспечивается определенная устойчивость параметров автоподстройки в условиях воздействия аддитивных помех.

Результаты исследования. Результаты исследования алгоритма (2) в случае, когда сигналы зависимы, выходят за рамки настоящей статьи. Однако уже полученные данные показали эффективность алгоритма вплоть до значений коэффициентов взаимной корреляции процессов ρ = 0,5–0,6. Это хорошо согласуется с результатами решения задач разнесенного приема [2–4]. Алгоритмы модифицированного комбинированного сложения сигналов эффективны и при разнесенном приеме, и в задачах принятия решения. Однако рассмотрение особенностей их реализации выходит за рамки статьи.

Итак, оптимизация процедуры принятия решения при обработке дискретных сигналов в условиях значительной априорной неопределенности может быть выполнена на основе непараметрических алгоритмов, основанных на эвристическом учете детальных характеристик взаимных превышений случайных процессов. Большее количество учитываемых детальных характеристик усложняет алгоритм. Однако именно такой алгоритм обеспечивает большую инвариантность по помехоустойчивости в условиях изменения длительности ожидаемых сигналов. Синтезированные алгоритмы могут быть реализованы в виде процедур дополнительной обработки на ЭВМ и технически — в виде аналоговых устройств [14, 19].