Линейные и нелинейные функции уголовного наказания (на примере США)
Автор: Ольков С.Г.
Журнал: Вестник Казанского юридического института МВД России @vestnik-kui-mvd
Рубрика: Уголовное право и криминология
Статья в выпуске: 3 (17), 2014 года.
Бесплатный доступ
Цель статьи - теоретическое обоснование полного набора математических функций уголовного наказания. Научные методы: 1) наблюдение; 2) дедукция; 3) использование законов формальной логики; 4) сравнительный анализ; 5) формально юридический; 6) математическое моделирование; 7) дифференциальное и интегральное исчисление; 8) исследование математических функций; 9) построение таблиц и графиков. Научные результаты, полученные автором: 1) теоретическое определение полного множества первообразных и дифференциальных линейных и нелинейных функций уголовного наказания с их параметризацией; 2) параметризация линейных - биссектриальной (базовой), надбиссектриальных и подбиссектриальных функций уголовного наказания;3) параметризация нелинейных функций уголовного наказания;4) параметризация и анализ первообразных, первых и вторых производных функций уголовного наказания в законодательстве и судебной практике США; 5) доказательство того, что в законодательстве и судебной практике США используются исключительно нелинейные - кубические, экспоненциальные и степенные функции уголовного наказания, зависящие от величины общественной опасности содеянного и общественной опасности лица, совершившего преступление; 6) анализ достоинств и недостатков «функций» наказания в США; 7) предложения по совершенствованию уголовных наказаний в России. Научная новизна заключается во вновь полученных научных результатах. Практическая значимость заключается в возможности использования полученных научных результатов в развитии уголовно-правовой и уголовно-процессуальной теорий; повышении уровня справедливости при вынесении судебных приговоров.
Приговор, преступление, уголовное наказание, правосудие, уголовное право, уголовный процесс, категории преступников, категории преступлений, математический анализ, аппроксимация, первообразные функции, производные функции, кубические функции, экспоненциальные функции, степенные функции, линейные функции, нелинейные функции
Короткий адрес: https://sciup.org/142197701
IDR: 142197701
Текст научной статьи Линейные и нелинейные функции уголовного наказания (на примере США)
Повышение эффективности уголовного наказания в противодействии преступному поведению является центральной задачей таких отраслевых юридических наук, как уголовное, уголовно-процессуальное и уголовно-исполнительное право. В представленном фундаментальном исследовании впервые в истории человечества показаны все теоретически возможные функции уголовного наказания в зависимости от факторов общественной опасности содеянного преступником и общественной опасности самого преступника, совершившего запрещенное уголовным законом деяние, что позволяет осуществить переход практики вынесения судебных приговоров и реализации уголовных наказаний на строгую математическую основу.
Примем допущение – уголовное наказание определяется двумя факторами: 1) количеством общественной опасности, содержащейся в запрещенном (преступном) деянии; 2) количеством общественной опасности, содержащейся в личности, его совершившей. Все остальные мыслимые факторы, влияющие на величину наказания, пока оставим за кадром, подобно сопротивлению воздуха в физике, изучающей падение тела с определенной высоты на Землю. Тогда математическая модель уголовного наказания имеет вид: y=f(xI,x:), где у - количество наказания, xI - количество общественной опасности, содержащейся в запрещенном (преступном) деянии; х2 - количество общественной опасности, содержащейся в личности, его совершившей; f - правило, связывающее левую и правую части уравнения. В неопределенном виде получена зависимость величины наказания от двух независимых переменных. Отсюда функция наказания будет представлена поверхностью в трёхмерном пространстве. Учитывая тот факт, что переменные х1 - количество общественной опасности, содержащейся в запрещенном (преступном) деянии; х2 -количество общественной опасности, содержащейся в личности, его совершившей, можно агрегировать в единую переменную, сведем модель до простой парной зависимости: y=f(x).
Теперь мы с большой легкостью можем описать бесконечное множество всех теоретически возможных функций уголовного наказания.
Функции уголовного наказания могут быть линейными и нелинейны-ми. Начнем с линейных как наиболее простых.
Самой простой линейной функцией уголовного наказания в зависимости от общественной опасности содеянного и общественной опасности совершившего деяния преступника, является биссектриальная функция: у=х (модель № 1), где у - величина наказания, х – величина преступления, с учетом личности, его совершившей. Параметры уравнения: а=0 (свободный член равен нулю, поскольку при отсутствии общественной опасности деяния и личности, его совершившей, уголовное наказание не применяется), b =1 (коэффициент пропорциональности (первая производная функции) – показывает, на сколько в абсолютном выражении изменяется наказание при изменении общественной опасности на единицу измерения. Для удобства вычислений и объяснения моделей будем измерять количество общественной опасности в баллах, а количество наказания – в годах лишения свободы. В этом случае работаем со шкалами отношений, ибо и баллы, и время можно дробить до бесконечности. Отсюда в модели № 1 наказание усиливается прямо пропорционально величине общественной опасно- сти с коэффициентом пропорциональности равным единице. Каждый дополнительный балл общественной опасности добавляет один год лишения свободы осужденному.
Модель № 1 назовем базовой и продолжим её характеристику. Очевидно, х >0, у >0, а =0, b =1. То есть геометрически модель представляется в первом квадранте декартовой (прямоугольной) системы координат. Очевидно, отрицательная общественная опасность и отрицательное наказание бессмысленны. Положительное и отрицательное ускорение как в базовой, так и иной линейной модели отсутствует.
Исследовав линейную базовую модель, опишем все иные линейные модели, которые возможны. Эти модели имеют следующие общие характеристики: х >0, у >0, а =0, b >0. То есть от базовой любая иная линейная модель отличается только по одной характеристике - величине параметра b . На этом основании все линейные модели нужно разделять на две группы: 1) надбиссектриаль-ные (назовем их «Н»-модели); 2) подбис-сектриальные (назовем их «П»-модели).
В «Н»-моделях параметр b >1. В «П»-мо-делях параметр b <1. Легко заметить, что базовая модель является промежуточной относительно «Н» и «П»-моделей. В «Н»-моделях более жесткое реагирование государства на преступное поведение, чем в базовой и «П»-моделях.
Нелинейные математические модели уголовного наказания отличаются от линейных только тем, что здесь параметр b≠const , и в модели наказания появляется положительное или отрицательное ускорение. То есть повышение общественной опасности на следующий балл (или часть балла) влечет большую (при положительном ускорении) или меньшую (при отрицательном) величину наказания, чем в предшествующей точке области определения функции наказания. Например, в экспоненциальной модели наказания ускорение положительно, а в логарифмической отрицательно.
Ниже я рассчитал функции уголовного наказания в зависимости от тяжести содеянного и личности преступника в США, поскольку именно в этом государстве вынесение судебных приговоров наиболее фор- мализовано и удобно рассчитывается.
For individuals, the fine table is as follows:
Таблица 1.
Величина минимального и максимального штрафа, налагаемого на физических лиц в США, в зависимости от уровня преступления.[1]
|
Offense level |
Minimum |
Maximum |
|
3 and below |
$100. |
$5,000. |
|
4-5 |
$250. |
$5,000. |
|
6-7 |
$500. |
$5,000. |
|
8-9 |
$1,000. |
$10,000. |
|
10-11 |
$2,000. |
$20,000. |
|
12-13 |
$3,000. |
$30,000. |
|
14-15 |
$4,000. |
$40,000. |
|
16-17 |
$5,000. |
$50,000. |
|
18-19 |
$6,000. |
$60,000. |
|
20-22 |
$7,500. |
$75,000. |
|
23-25 |
$10,000. |
$100,000. |
|
26-28 |
$12,500. |
$125,000. |
|
29-31 |
$15,000. |
$150,000. |
|
32-34 |
$17,500. |
$175,000. |
|
35-37 |
$20,000. |
$200,000. |
|
38 and above |
$25,000. |
$250,000. |
Рисунок 2.
Функция штрафов (в максимуме) в зависимости от уровня преступления в США (таблица для расчета функции приведена в приложении: таблица 2).
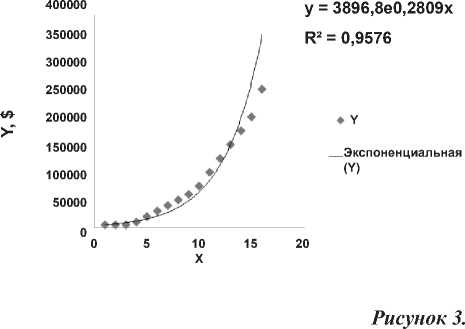
Функция минимального наказания
(в месяцах заключения) I категории преступников в США в зависимости от тяжести содеянного (таблица для расчета функции приведена в приложении: таблица 3).
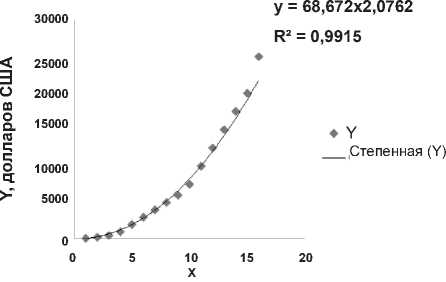
Рисунок 1.
Функция штрафов (в минимуме) в зависимости от уровня преступления в США (таблица для расчета функции приведена в приложении: таблица 1).
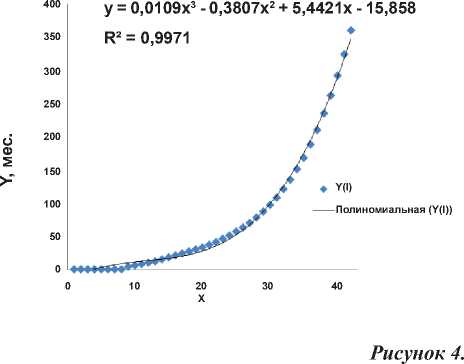
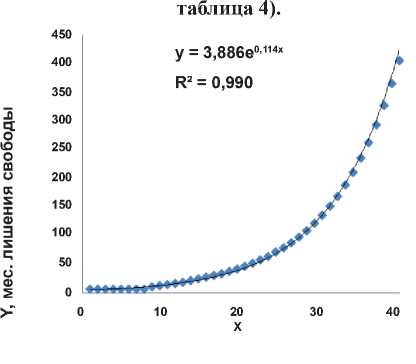
Функция максимального наказания (в месяцах заключения) I категории преступников в США в зависимости от тяжести содеянного (таблица для расчета функции приведена в приложении:
ВЕСТНИК
Казанского юридического института МВД России № 3(17) 2014
Таблица 3.
Первообразные функции наказания преступников разных категорий в США в зависимости от тяжести содеянного.
|
Категории преступников в США |
Функция наказания в минимуме |
Функция наказания в максимуме |
|
I |
yI (min) = 0,010 x 3 - 0,380 x 2 + 5,442 x - 15,85 |
y I (max) = 3,886 e 0,114 x |
|
II |
yII (min) = 0,011 x 3 - 0,393 x 2 + 5,640 x - 15,65 |
yII (max) = 4,364 e 0,114 x |
|
III |
yIII (min) = 0,012 x 3 - 0,405 x 2 + 5,821 x - 15,44 |
yIII (max) = 4,788 e 0,115 x |
|
IV |
yIV (min) = 0,013 x 3 - 0,436 x 2 + 6,658 x - 16,53 |
y IV (max) = 6,122 e 0,112 x |
|
V |
yV (min) = 0,013 x 3 - 0,430 x 2 + 7,093 x - 16,46 |
y V (max) = 7,622 e 0,110 x |
|
VI |
yVI (min) = 0,014 x 3 - 0,451 x 2 + 7,411 x - 15,62 |
y VI (max) = 8,647 e 0,109 x |
Таблица 3.
Первообразные функции наказания преступников разных категорий в США в зависимости от тяжести содеянного.
|
Функция наказания |
dx y ( x ) |
d 2 dx 2 y ( x ) |
|
y I (min) |
0,03 x 2 - 0,76 x + 5,44 |
0,06 x - 0,76 |
|
y II (min) |
0,033 x 2 - 0,786 x + 5,64 |
0,066 x - 0,786 |
|
y III (min) |
0,036 x 2 - 0,81 x + 5,82 |
0,072 x - 0,81 |
|
y IV (min) |
0,039 x 2 - 0,872 x + 6,658 |
0,078 x - 0,872 |
|
y V (min) |
0,039 x 2 - 0,86 x + 7,093 |
0,078 x - 0,86 |
|
y VI (min) |
0,042 x 2 - 0,902 x + 7,441 |
0,084 x - 0,902 |
Таблица 2.
Таблица приговоров в месяцах заключения в зависимости от уровня преступления и категории криминальной истории преступника в США (на ноябрь 2012 года).[1]
Sentencing Table (effective Nov. 2012) (showing months of imprisonment )
|
Offense Level |
Criminal History Category (Criminal History Points) |
||||||
|
I (0 or 1) |
II (2 or 3) |
III (4,5,6) |
IV (7,8,9) |
V (10,11,12) |
VI (13+) |
||
|
Zone A |
1 |
0-6 |
0-6 |
0-6 |
0-6 |
0-6 |
0-6 |
|
2 |
0-6 |
0-6 |
0-6 |
0-6 |
0-6 |
1-7 |
|
|
3 |
0-6 |
0-6 |
0-6 |
0-6 |
2-8 |
3-9 |
|
|
4 |
0-6 |
0-6 |
0-6 |
2-8 |
4-10 |
6-12 |
|
|
5 |
0-6 |
0-6 |
1-7 |
4-10 |
6-12 |
9-15 |
|
|
6 |
0-6 |
1-7 |
2-8 |
6-12 |
9-15 |
12-18 |
|
|
7 |
0-6 |
2-8 |
4-10 |
8-14 |
12-18 |
15-21 |
|
|
8 |
0-6 |
4-10 |
6-12 |
10-16 |
15-21 |
18-24 |
|
|
Zone B |
9 |
4-10 |
6-12 |
8-14 |
12-18 |
18-24 |
21-27 |
|
10 |
6-12 |
8-14 |
10-16 |
15-21 |
21-27 |
24-30 |
|
|
11 |
8-14 |
10-16 |
12-18 |
18-24 |
24-30 |
27-33 |
|
|
Zone C |
12 |
10-16 |
12-18 |
15-21 |
21-27 |
27-33 |
30-37 |
|
13 |
12-18 |
15-21 |
18-24 |
24-30 |
30-37 |
33-41 |
|
|
Zone D |
14 |
15-21 |
18-24 |
21-27 |
27-33 |
33-41 |
37-46 |
|
15 |
18-24 |
21-27 |
24-30 |
30-37 |
37-46 |
41-51 |
|
|
16 |
21-27 |
24-30 |
27-33 |
33-41 |
41-51 |
46-57 |
|
|
17 |
24-30 |
27-33 |
30-37 |
37-46 |
46-57 |
51-63 |
|
|
18 |
27-33 |
30-37 |
33-41 |
41-51 |
51-63 |
57-71 |
|
|
19 |
30-37 |
33-41 |
37-46 |
46-57 |
57-71 |
63-78 |
|
|
20 |
33-41 |
37-46 |
41-51 |
51-63 |
63-78 |
70-87 |
|
|
21 |
37-46 |
41-51 |
46-57 |
57-71 |
70-87 |
77-96 |
|
|
22 |
41-51 |
46-57 |
51-63 |
63-78 |
77-96 |
84-105 |
|
|
23 |
46-57 |
51-63 |
57-71 |
70-87 |
84-105 |
92-115 |
|
|
24 |
51-63 |
57-71 |
63-78 |
77-96 |
92-115 |
100-125 |
|
|
25 |
57-71 |
63-78 |
70-87 |
84-105 |
100-125 |
110-137 |
|
|
26 |
63-78 |
70-87 |
78-97 |
92-115 |
110-137 |
120-150 |
|
|
27 |
70-87 |
78-97 |
87-108 |
100-125 |
120-150 |
130-162 |
|
|
28 |
78-97 |
87-108 |
97-121 |
110-137 |
130-162 |
140-175 |
|
|
29 |
87-108 |
97-121 |
108-135 |
121-151 |
140-175 |
151-188 |
|
|
30 |
97-121 |
108-135 |
121-151 |
135-168 |
151-188 |
168-210 |
|
|
31 |
108-135 |
121-151 |
135-168 |
151-188 |
168-210 |
188-235 |
|
|
32 |
121-151 |
135-168 |
151-188 |
168-210 |
188-235 |
210-262 |
|
|
33 |
135-168 |
151-188 |
168-210 |
188-235 |
210-262 |
235-293 |
|
|
34 |
151-188 |
168-210 |
188-235 |
210-262 |
235-293 |
262-327 |
|
|
35 |
168-210 |
188-235 |
210-262 |
235-293 |
262-327 |
292-365 |
|
|
36 |
188-235 |
210-262 |
235-293 |
262-327 |
292-365 |
324-405 |
|
|
37 |
210-262 |
235-293 |
262-327 |
292-365 |
324-405 |
360-life |
|
|
38 |
235-293 |
262-327 |
292-365 |
324-405 |
360-life |
360-life |
|
|
39 |
262-327 |
292-365 |
324-405 |
360-life |
360-life |
360-life |
|
|
40 |
292-365 |
324-405 |
360-life |
360-life |
360-life |
360-life |
|
|
41 |
324-405 |
360-life |
360-life |
360-life |
360-life |
360-life |
|
|
42 |
360-life |
360-life |
360-life |
360-life |
360-life |
360-life |
|
|
43 |
life |
life |
life |
life |
life |
life |
Таблица 5.
Первые (скорость) и вторые (ускорение) производные функции наказания преступников в США в зависимости от категории преступников и тяжести содеянного (в максимуме).
|
Функция наказания |
dx y ( x ) |
d 2 dx 2 y ( x ) |
|
y I (max) |
0,0443 e 0,114 x |
0,0505 e 0,114 x |
|
y II (max) |
0,0497 e 0,114 x |
0,0567 e 0,114 x |
|
y III (max |
0,5506 e 0,115 x |
0,0633 e 0,115 x |
|
y IV (max) |
0,6856 e 0,112 x |
0,07679 e 0,112 x |
|
y V (max) |
0,8384 e 0,110 x |
0,092 e 0,110 x |
|
y VI (max) |
0,943 e 0,109 x |
0,102 e 0,109 x |
Очевидно, между функциями в минимуме и максимуме теоретически существует бесконечное множество функций. Например, можно получить среднюю функцию. Ниже приведен пример средней функции для преступников первой категории.
Рисунок 5.
Средняя функция наказания преступников в США в зависимости от категории преступников и тяжести содеянного на примере первой категории преступников.
(ymax+ymin)/2
y = 0,0121x3 - 0,4335x2 + 5,8726x - 13,531
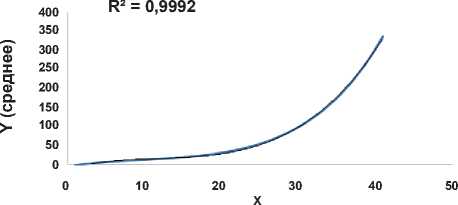
В таблице 5 приложения приведены вычисления к вышеприведенному рисунку.
Говоря об особенностях американской (США) системы уголовных наказаний, важно отметить то неоспоримое достоинство, что здесь четко выделены и связаны между собой две ранговые шкалы : 1) шкала общественной опасности преступлений; 2) шкала общественной опасности преступников. Это делает систему уголовных наказаний в США, во-первых, прозрачной; во-вторых, удобной в практическом применении; в-третьих, наиболее точной относительно существующих на планете систем уголовного наказания, открывающей широкие возможности для научной работы и дальнейшего совершенствования системы наказаний.
Основными недостатками американской системы наказаний являются, во-первых, её дискретный характер; во-вторых, ранговые шкалы; в-третьих, большой размах между минимальными и максимальными значениями наказания по соответствующим категориям преступников. То есть систему нужно совершенствовать в этом направлении: 1) переходить от дискретных оценок (табличных) к непрерывным функциям; 2) переходить от ранговых шкал к шкалам отношений; 3) сводить к нулю разрыв между минимальными и максимальными значениями наказаний по категориям преступников (переходить к однозначным функциям наказания по категориям преступников). Если устранить эти недостатки, то система станет предельно точной и эффективной. По сути, когда я применил аппроксимацию дискретных табличных данных об общественной опасности преступлений и преступников, то, во-первых, перешел к шкалам отношений, а во-вторых, к непрерывным данным. Преимущество здесь очевидно, поскольку, имея в руках функцию уголовного наказания, судья со сколь угодно высокой степенью точности выставляет оценку содеянного преступником – вплоть до секунд, которые должен будет отбыть осужденный. Если судьей точно диагностировано деяние подсудимого в области определения функции, то, подставив его величину в уравнение, он тут же совершенно точно получит величину наказания, которую следует назначить (значение функции уголовной ответственности).
Совершенствование российского уголовного, уголовно-процессуального законодательства и судебной практики с неизбежностью будет идти именно по этому пути, ибо никакого альтернативного не существует. Нам необходимо: во-первых, четко шкалировать ось общественной опасности деяний; во-вторых, четко шкалировать ось общественной опасности преступников; в-третьих, проводить четкую параметри- зацию уравнений уголовной ответственности, дабы выносить справедливые (точные), обоснованные и законные приговоры.
Выводы
-
1) Получена базовая биссектриальная функция уголовного наказания: y=x , где у – величина наказания, x – величина преступления с учетом личности, его совершившей: х ≥0, y ≥0, параметры уравнения: а =0, b =1. Свободный член равен нулю, поскольку при отсутствии общественной опасности деяния и личности, его совершившей, уголовное наказание не применяется. Коэффициент пропорциональности в базовой модели b =1. Это означает, что изменение независимой переменной x на единицу измерения (1 балл) влечет изменение величины наказания y строго на единицу.
-
2) Все иные линейные модели относительно базовой нужно свести к двум типам: 1) надбиссектриальные («Н»-модели); 2) подбиссектриальные («П»-модели). Эти модели имеют следующие общие характеристики: х ≥0, y ≥0, а =0, b >0. То есть от базовой любая иная линейная модель отличается только по одной характеристике – величине параметра b .
-
3) В «Н»-моделях параметр b >1. В «П»-моделях параметр b <1. Базовая модель является промежуточной относительно «Н» и «П»-моделей. В «Н»-моделях более жесткое реагирование государства на преступное поведение, чем в базовой и «П»-моделях.
-
4) Нелинейные математические модели уголовного наказания отличаются от линейных только тем, что здесь параметр b≠const , и в модели наказания появляется положительное или отрицательное ускорение.
-
5) Вольно или невольно законодательство и судебная практика любого государства принимают ту или иную математическую модель уголовного наказания (осознавая это или нет). Чрезвычайно важно, чтобы теоретики уголовного права ясно представляли себе математическую модель уголовного наказания в их государстве в каждый конкретный момент его существования. В этом случае существенно возрастает понимание сути происходящего в уголовно-правовых явлениях и процессах, расширяется
плацдарм реальных научных изысканий в области уголовного права, отыскивается наиболее эффективная функция уголовного наказания.
-
6) Как видно из моих расчетов, в законодательстве и судебной практике США приняты на вооружение нелинейные кубические, экспоненциальные и степенные функции наказания, которые отражают уголовно-правовые идеи о том, что, во-первых, при вынесении судебного приговора важно строго учитывать общественную опасность содеянного, а во-вторых, уровень общественной опасности лица, совершившего преступление. Отсюда, во-первых, наказание ускоренно (с положительным ускорением) возрастает по любой категории преступников в зависимости от тяжести содеянного. Во-вторых, наказание усиливается быстрей с повышением уровня общественной опасности преступника (с повышением категории), о чем наглядно свидетельствуют функции наказания различных категорий преступников в США.
-
7) Показаны достоинства и недостатки математической модели уголовных наказаний в США.
-
8) Предложены меры совершенствования системы наказаний в России: 1) необходимо четко шкалировать ось общественной опасности деяний; во-вторых, четко шкалировать ось общественной опасности преступников; в-третьих, проводить четкую параметризацию уравнений уголовной ответственности, дабы выносить справедливые (точные), обоснованные и законные приговоры.
Приложение.
Таблица 1.
Данные для получения функции штрафов (минимум) в США в зависимости от категории преступления.
|
Минимум |
X |
Y |
|
$100. |
1 |
100 |
|
$250. |
2 |
250 |
|
$500. |
3 |
500 |
|
$1,000. |
4 |
1000 |
|
$2,000. |
5 |
2000 |
|
$3,000. |
6 |
3000 |
|
$4,000. |
7 |
4000 |
|
$5,000. |
8 |
5000 |
|
$6,000. |
9 |
6000 |
|
$7,500. |
10 |
7500 |
|
$10,000. |
11 |
10000 |
|
$12,500. |
12 |
12500 |
|
$15,000. |
13 |
15000 |
|
$17,500. |
14 |
17500 |
|
$20,000. |
15 |
20000 |
|
$25,000. |
16 |
25000 |
Таблица 2.
Данные для получения функции штрафов (максимум) в США в зависимости от категории преступления.
|
Максимум |
Х |
Y |
|
$5,000. |
1 |
5000 |
|
$5,000. |
2 |
5000 |
|
$5,000. |
3 |
5000 |
|
$10,000. |
4 |
10000 |
|
$20,000. |
5 |
20000 |
|
$30,000. |
6 |
30000 |
|
$40,000. |
7 |
40000 |
|
$50,000. |
8 |
50000 |
|
$60,000. |
9 |
60000 |
|
$75,000. |
10 |
75000 |
|
$100,000. |
11 |
100000 |
|
$125,000. |
12 |
125000 |
|
$150,000. |
13 |
150000 |
|
$175,000. |
14 |
175000 |
|
$200,000. |
15 |
200000 |
|
$250,000. |
16 |
250000 |
Таблица 3.
Данные для расчета функций наказания преступников в США (в минимуме) (без учета пожизненного заключения – пустые ячейки).
|
X |
Y(I) |
Y(II) |
Y(III) |
Y(IV) |
Y(V) |
Y(VI) |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
2 |
0 |
0 |
0 |
0 |
0 |
1 |
|
3 |
0 |
0 |
0 |
0 |
2 |
3 |
|
4 |
0 |
0 |
0 |
2 |
4 |
6 |
|
5 |
0 |
0 |
1 |
4 |
6 |
9 |
|
6 |
0 |
1 |
2 |
6 |
9 |
12 |
|
7 |
0 |
2 |
4 |
8 |
12 |
15 |
|
8 |
0 |
4 |
6 |
10 |
15 |
18 |
|
9 |
4 |
6 |
8 |
12 |
18 |
21 |
|
10 |
6 |
8 |
10 |
15 |
21 |
24 |
|
11 |
8 |
10 |
12 |
18 |
24 |
27 |
|
12 |
10 |
12 |
15 |
21 |
27 |
30 |
|
13 |
12 |
15 |
18 |
24 |
30 |
33 |
|
14 |
15 |
18 |
21 |
27 |
33 |
37 |
|
15 |
18 |
21 |
24 |
30 |
37 |
41 |
|
16 |
21 |
24 |
27 |
33 |
41 |
46 |
|
17 |
24 |
27 |
30 |
37 |
46 |
51 |
|
18 |
27 |
30 |
33 |
41 |
51 |
57 |
|
19 |
30 |
33 |
37 |
46 |
57 |
63 |
|
20 |
33 |
37 |
41 |
51 |
63 |
70 |
|
21 |
37 |
41 |
46 |
57 |
70 |
77 |
|
22 |
41 |
46 |
51 |
63 |
77 |
84 |
|
23 |
46 |
51 |
57 |
70 |
84 |
92 |
|
24 |
51 |
57 |
63 |
77 |
92 |
100 |
|
25 |
57 |
63 |
70 |
84 |
100 |
110 |
|
26 |
63 |
70 |
78 |
92 |
110 |
120 |
|
27 |
70 |
78 |
87 |
100 |
120 |
130 |
|
28 |
78 |
87 |
97 |
110 |
130 |
140 |
|
29 |
87 |
97 |
108 |
121 |
140 |
151 |
|
30 |
97 |
108 |
121 |
135 |
151 |
168 |
|
31 |
108 |
121 |
135 |
151 |
168 |
188 |
|
32 |
121 |
135 |
151 |
168 |
188 |
210 |
|
33 |
135 |
151 |
168 |
188 |
210 |
235 |
|
34 |
151 |
168 |
188 |
210 |
235 |
262 |
|
35 |
168 |
188 |
210 |
235 |
262 |
292 |
|
36 |
188 |
210 |
235 |
262 |
292 |
324 |
|
37 |
210 |
235 |
262 |
292 |
324 |
360 |
|
38 |
235 |
262 |
292 |
324 |
360 |
|
|
39 |
262 |
292 |
324 |
360 |
||
|
40 |
292 |
324 |
360 |
|||
|
41 |
324 |
360 |
||||
|
42 |
360 |
Рисунок 1.
Функция наказания (в месяцах заключения) II категории преступников в США в зависимости от тяжести содеянного (в минимуме).
Y, мес.
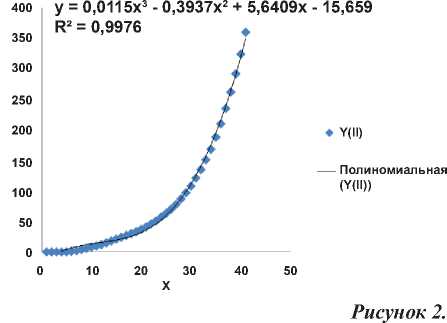
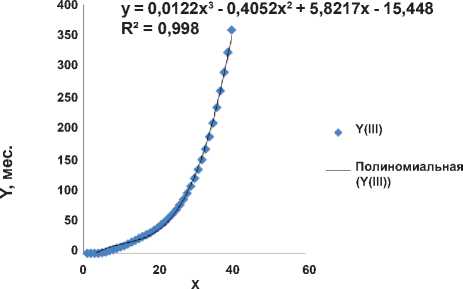
Рисунок 3.
Функция наказания (в месяцах заключения) IV категории преступников в США в зависимости от тяжести содеянного (в минимуме).
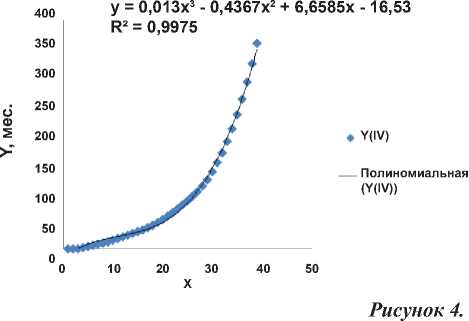
Функция наказания (в месяцах заключения) III категории преступников в США в зависимости от тяжести содеянного (в минимуме).
Функция наказания (в месяцах заключения) V категории преступников в США в зависимости от тяжести содеянного (в минимуме).
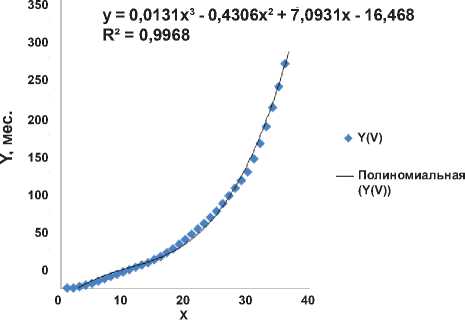
Рисунок 5. Функция наказания (в месяцах заключения) VI категории преступников в США в зависимости от тяжести содеянного (в минимуме).
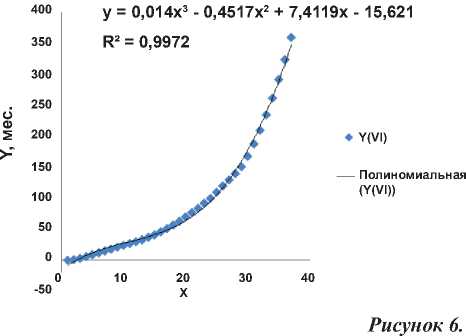
Функция наказания (в месяцах заключения) II категории преступников в США в зависимости от тяжести содеянного (в максимуме).
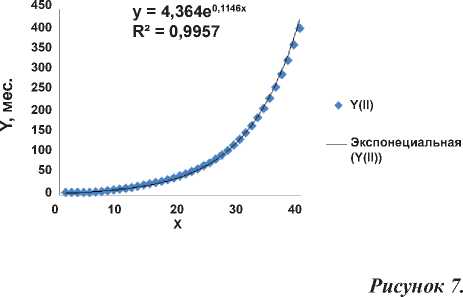
Функция наказания (в месяцах заключения) III категории преступников в США в зависимости от тяжести содеянного (в максимуме).
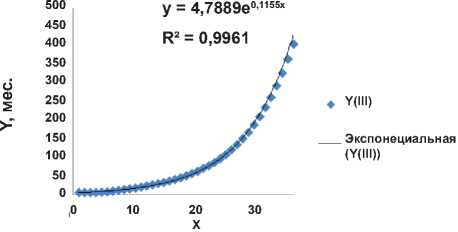
Рисунок 8. Функция наказания (в месяцах заключения) IV категории преступников в США в зависимости от тяжести содеянного (в максимуме).
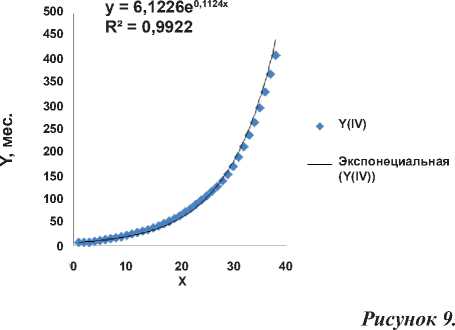
Функция наказания (в месяцах заключения) V категории преступников в США в зависимости от тяжести содеянного (в максимуме).
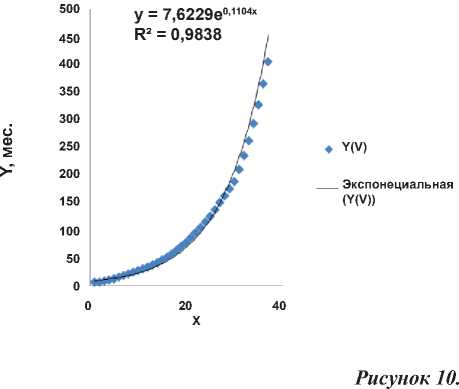
Функция наказания (в месяцах заключения) VI категории преступников в США в зависимости от тяжести содеянного (в максимуме).
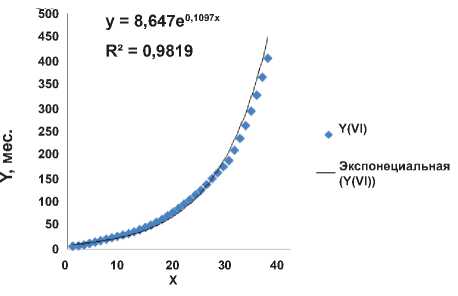
Таблица 4.
Данные для расчета функций наказания преступников в США (в максимуме)
(без учета пожизненного заключения – пустые ячейки).
|
X |
Y(I) |
Y(II) |
Y(III) |
Y(IV) |
Y(V) |
Y(VI) |
|
1 |
6 |
6 |
6 |
6 |
6 |
6 |
|
2 |
6 |
6 |
6 |
6 |
6 |
7 |
|
3 |
6 |
6 |
6 |
6 |
8 |
9 |
|
4 |
6 |
6 |
6 |
8 |
10 |
12 |
|
5 |
6 |
6 |
7 |
10 |
12 |
15 |
|
6 |
6 |
7 |
8 |
12 |
15 |
18 |
|
7 |
6 |
8 |
10 |
14 |
18 |
21 |
|
8 |
6 |
10 |
12 |
16 |
21 |
24 |
|
9 |
10 |
12 |
14 |
18 |
24 |
27 |
|
10 |
12 |
14 |
16 |
21 |
27 |
30 |
|
11 |
14 |
16 |
18 |
24 |
30 |
33 |
|
12 |
16 |
18 |
21 |
27 |
33 |
37 |
|
13 |
18 |
21 |
24 |
30 |
37 |
41 |
|
14 |
21 |
24 |
27 |
33 |
41 |
46 |
|
15 |
24 |
27 |
30 |
37 |
46 |
51 |
|
16 |
27 |
30 |
33 |
41 |
51 |
57 |
|
17 |
30 |
33 |
37 |
46 |
57 |
63 |
|
18 |
33 |
37 |
41 |
51 |
63 |
71 |
|
19 |
37 |
41 |
46 |
57 |
71 |
78 |
|
20 |
41 |
46 |
51 |
63 |
78 |
87 |
|
21 |
46 |
51 |
57 |
71 |
87 |
96 |
|
22 |
51 |
57 |
63 |
78 |
96 |
105 |
|
23 |
57 |
63 |
71 |
87 |
105 |
115 |
|
24 |
63 |
71 |
78 |
96 |
115 |
125 |
|
25 |
71 |
78 |
87 |
105 |
125 |
137 |
|
26 |
78 |
87 |
97 |
115 |
137 |
150 |
|
27 |
87 |
97 |
108 |
125 |
150 |
162 |
|
28 |
97 |
108 |
121 |
137 |
162 |
175 |
|
29 |
108 |
121 |
135 |
151 |
175 |
188 |
|
30 |
121 |
135 |
151 |
168 |
188 |
210 |
|
31 |
135 |
151 |
168 |
188 |
210 |
235 |
|
32 |
151 |
168 |
188 |
210 |
235 |
262 |
|
33 |
168 |
188 |
210 |
235 |
262 |
293 |
|
34 |
188 |
210 |
235 |
262 |
293 |
327 |
|
35 |
210 |
235 |
262 |
293 |
327 |
365 |
|
36 |
235 |
262 |
293 |
327 |
365 |
405 |
|
37 |
262 |
293 |
327 |
365 |
405 |
|
|
38 |
293 |
327 |
365 |
405 |
||
|
39 |
327 |
365 |
405 |
|||
|
40 |
365 |
405 |
||||
|
41 |
405 |
Таблица 5.
Вычисление средней функции наказания преступников различных категорий в США в зависимости от тяжести содеянного на примере первой категории преступников.
|
X |
ymax |
ymin |
(ymax+ymin)/2 |
|
1 |
4,355243 |
-10,778 |
-3,2 |
|
2 |
4,881148 |
-6,406 |
-0,8 |
|
3 |
5,470557 |
-2,674 |
1,4 |
|
4 |
6,131138 |
0,478 |
3,3 |
|
5 |
6,871486 |
3,11 |
5,0 |
|
6 |
7,701232 |
5,282 |
6,5 |
|
7 |
8,631172 |
7,054 |
7,8 |
|
8 |
9,673405 |
8,486 |
9,1 |
|
9 |
10,84149 |
9,638 |
10,2 |
|
10 |
12,15062 |
10,57 |
11,4 |
|
11 |
13,61784 |
11,342 |
12,5 |
|
12 |
15,26222 |
12,014 |
13,6 |
|
13 |
17,10516 |
12,646 |
14,9 |
|
14 |
19,17065 |
13,298 |
16,2 |
|
15 |
21,48554 |
14,03 |
17,8 |
|
16 |
24,07997 |
14,902 |
19,5 |
|
17 |
26,98768 |
15,974 |
21,5 |
|
18 |
30,2465 |
17,306 |
23,8 |
|
19 |
33,89882 |
18,958 |
26,4 |
|
20 |
37,99218 |
20,99 |
29,5 |
|
21 |
42,57982 |
23,462 |
33,0 |
|
22 |
47,72142 |
26,434 |
37,1 |
|
23 |
53,48388 |
29,966 |
41,7 |
|
24 |
59,94218 |
34,118 |
47,0 |
|
25 |
67,18032 |
38,95 |
53,1 |
|
26 |
75,29249 |
44,522 |
59,9 |
|
27 |
84,38421 |
50,894 |
67,6 |
|
28 |
94,57379 |
58,126 |
76,3 |
|
29 |
105,9938 |
66,278 |
86,1 |
|
30 |
118,7927 |
75,41 |
97,1 |
|
31 |
133,1372 |
85,582 |
109,4 |
|
32 |
149,2138 |
96,854 |
123,0 |
|
33 |
167,2317 |
109,286 |
138,3 |
|
34 |
187,4253 |
122,938 |
155,2 |
|
35 |
210,0573 |
137,87 |
174,0 |
|
36 |
235,4222 |
154,142 |
194,8 |
|
37 |
263,8499 |
171,814 |
217,8 |
|
38 |
295,7103 |
190,946 |
243,3 |
|
39 |
331,418 |
211,598 |
271,5 |
|
40 |
371,4374 |
233,83 |
302,6 |
|
41 |
416,2893 |
257,702 |
337,0 |
Список литературы Линейные и нелинейные функции уголовного наказания (на примере США)
- URL: http://www.ussc.gov


