Линии тока для решения Прандтля

Рассмотрим уравнение идеальной пластичности в форме Сен-Венана-Леви. Они имеют вид

6g ( d0        50) _

--2I —cos20+ sin20 I = 0, 8x ( dx        8y

8g ( d0        80) „

--2I —sin20 cos20 I = 0, 8y ( dx        8y

(Sv   8vv)       Svd

I +     I tg2 0 + —^---- y = 0,

( 8y   8x J       8x

8Vc dvy л +=

8x где g - гидростатическое давление; 0 - угол между первым главным направлением тензора напряжений и осью OX; vx,vy – компоненты вектора скорости, постоянная пластичности для простоты положена равной единице.

Уравнения (1), (2) описывают напряженно-деформированное состояние пластической среды.

Система уравнений (1)–(2) уже достаточно подробно изучена. Для нее известны группы симметрий, законы сохранения, точные решения. Обзор этих и других результатов можно найти в [1; 2].

Наиболее известное решение уравнений (1) – это решение Прандтля, которое можно использовать для описания напряженного состояния пластического слоя, сжимаемого жесткими плитами:

g = - x - 7 1 - y ² , y = cos 2 0 .        (3)

Подставляя (3) в систему (2) получаем систему линейных уравнений для определения полей скоростей совместных с этим решением.

Наиболее известное решение системы (4) – решение Надаи, которое имеет вид vx = x + 271- y2, vy = -y.         (5)

В [3; 4] приведены другие решения системы (4).

Там же показано, что решение (5) не дает максимум диссипации энергии во всей области | y | <  1.

Поэтому для описания деформируемого состояния следует использовать и другие поля скоростей. Приведем наиболее простое новое решение системы (4)

• ⁽ / 1 + y   /1 - y )    ⁽- x - 7 1 - y ²

• v. = J-- J ---- exp ------------ ,

x (V 2 V 2 J I 2

• ⁽ 1 1 + y    1 1 - y )    ⁽ - x - 71 - y ²

v y =H~⁺V ~ J ^exp I--- 2--- 1 .

Для более полного анализа напряженно-деформированного состояния, кроме формул (4)–(6), необходимо использовать линии скольжения и линии тока. В данном случае нельзя использовать траектории движения точек среды, поскольку время явно не входит в уравнения (1)–(2). Использование временно-подоб ных параметров [5], по нашему мнению, спорно.

Линии скольжения для решения Прандтля известны и являются частями циклоид (рис. 1).

Для построения линий тока следует решить систему уравнений dx dy

V = ^.

xy

Для решения Надаи эта система сводится к квадратуре d (xy) = 71 - y2dy,

• (    8v, 8v ) J1 - y2

I x + p--- +_ ₊ 2 _2x = 0,

• (    8y   8x J y

• 8 v_x 8 v

• —— + —4y = 0.

dx поэтому линии тока имеют вид x = f (71- y2)/ydy =

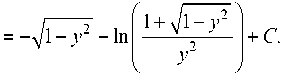
Эти линии тока приведены на рис. 2.

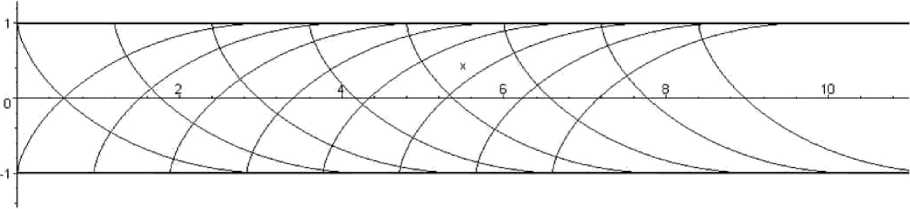
Рис. 1. Линии скольжения для решения Прандтля

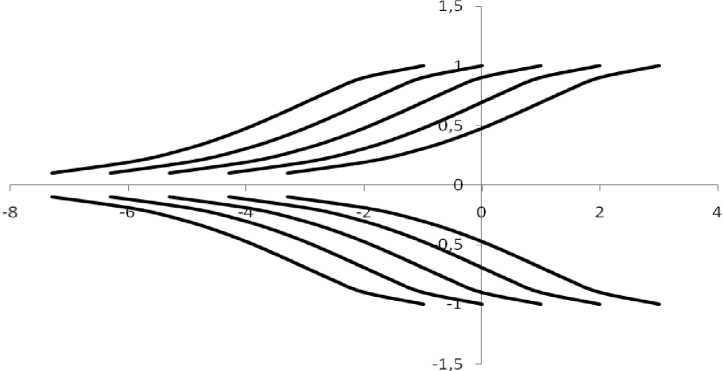
Рис. 2. Линии скольжения для решения Надаи

Найдем линии тока для поля скоростей (6). После несложных преобразований получаем

dx              dy

1++у - 1-2 1+2 + 1+2'

Вычисляя квадратуры, получаем поле линий тока, совпадающее с (7).

Для дальнейшего анализа построенных решений вычислим диссипацию энергии для полей скоростей (5) и (6) и сравним полученные результаты. Известно, что согласно модифицированному принципу максимума Мизеса [6], на действительном поле скоростей диссипация должна быть максимальна:

*

^ y e y — ^M y e y ,

где величины без звездочек – действительные компоненты тензора напряжений и тензора скоростей деформации, а со звездочкой – возможные.

Вычислим диссипацию:

D = ^ xex +C yey + 2t exy =

ex+e2+2 ey ex+ ey+2 eXy

= V e x ⁺ e y ^{+ x} e xy •

Поскольку e x = e y , ² e xy = e x 2_ = H ( y ) e x , то A i - y

D = e x | V 2 + H ² ( y ) .

Для решения Надаи диссипация равна

D_x = 72 + H ² ( y ) .

Для решения (6) аналогично получаем

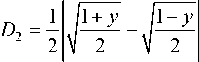
D ₁ exp

- X - 1- - y2

A

Из сравнения D i и D ₂ следует, что при x >  0 есть области, где предпочтительнее поле скоростей Надаи, а при x <  0 есть области, где предпочтительнее поле скоростей (6).

Из полученных результатов следует, что известное поле скоростей Надаи не всегда является предпочтительным перед другими полями скоростей. А поскольку система уравнений (4) имеет бесконечно много решений, то задачу по построению полей скоростей, соответствующих решению Прандтля, нельзя считать окончательно решенной.