Local search in bilinear two-person game
Автор: Khamisov O.V., Minarchenko I.M.
Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau
Рубрика: Математика, механика, информатика
Статья в выпуске: 1 т.17, 2016 года.
Бесплатный доступ
We consider an approach that allows reducing Nash equilibrium problem to a minimax problem for rather wide class of games using the so-called Nikaido-Isoda function. One can reformulate minimax problem as an optimization problem with nonconvex and implicitly defined objective function in general case. In other words, the set of Nash equilibria of the game is coincide with the set of global solutions of derived optimization problem. In present paper we investigate such an approach as applied to bilinear two-person game with quadratic loss functions and independent strategy spaces in view of an assumption that loss functions are strictly convex with respect to own players’ variables. In this case we suggest to replace “inner” optimization problem in minimax problem by Lagrange dual one. Such a way leads to presentation of the objective function as a difference of two convex functions (d.c-decomposition of the objective function). The very function in d.c-decomposition, that forms concave part, is defined implicitly as well as the objective function. We propose a method for linearization of concave term. That allows using the well-known local search method for d.c-functions, where the next iteration point is a solution of convex optimization problem with the objective function, which gained from initial objective by linearization of concave term in d.c-decomposition. Since the concerned problem is nonconvex, we offer to use local search in combination with multistart. The results of computational experiment are provided in the paper.
Nash equilibrium, nikaido-isoda function, d.c-decomposition, d.c-разложение
Короткий адрес: https://sciup.org/148177556
IDR: 148177556 | УДК: 519.833
Текст научной статьи Local search in bilinear two-person game
Introduction. In present paper we consider bilinear games in the sense of the definition given in [1]. It means that we investigate bilinear games with loss functions, which are quadratic with respect to own players’ vari- ables. Bilinear games represent a rather wide class, which includes in particular mixed extension of bimatrix games as well as of polymatrix games (see for details and more examples [2]). A lot of investigations were devoted to computing mixed Nash equilibrium in bimatrix games and related topics (see, for example [3]). Another approach can be found in [4]. In [5] one can find method for solving mixed extension of finite games with three players. Research in [2] is devoted to existence and constructing of polynomial time algorithms for bilinear games with fixed rank of the sum of player’s payoff (loss) matrices. In what follows we assume that the loss function of each player is strictly convex with respect to its strategy. Hence, by the well-known facts from game theory there exists a solution of the game. However, even under these assumptions we have a very difficult computational problem. The bimatrix game is a particular case of the game considered in our paper. In [6] it was shown that bimatrix game could have an exponential number of equilibrium points.
Problem statement. Let us consider bilinear two-person game [1]
F 1 ( x 1 , x 2 ) = x T ( C 1 x 2 + d 1 ) +
+ — x T Bx ^ min, x e X 1 , 2 x 1
F 2 ( x 1 , x 2 ) = x T ( C 2 x 1 + d 2 ) +
+ 1 x T B 2 x 2 ^ min, x 2 e X 2, 2 x 2
where X 1 and X 2 are non-empty, compact, convex sets of form
X 1 = | x 1 e R m1 | A 1 x 1 < b 1 j ,
X 2 = | x 2 e R m 2 | A 2 x 2 < b 2 j .
Here d 1 e R m 1 , d 2 e R m 2 , b 1 e R q1 , b 2 e R q 2 and matrices C 1 , C 2, B 1 , B 2, A 1 , A 2 have sizes m 1 x m 2, m 2 x m 1 , m 1 x m 1 , m 2 x m 2, q 1 x m 1 , q 2 x m 2 respectively. Without loss of generality, we suppose B 1 and B 2 to be symmetric matrices. R is a set of real numbers. In contrast to the game statement in [2], we add quadratic part to the each loss function and do not make any assumptions about rank of matrices in bilinear part.
Reduction and algorithm. Consider a function
Ф( x 1 , x 2 , У 1 , y 2 ) = F 1 ( x 1 , y 2 ) + F 2 ( У 1 , x 2 )
and denote x = ( x 1 , x 2 ) , y = ( y 1 , y 2 ) . Let us introduce the Nikaido–Isoda function [7; 8]
¥ ( x , y ) = Ф ( y , y ) -Ф ( x , y ) , which is real-valued function defined on the Cartesian product X x X , where X = X 1 x X 2.
Theorem [6]. The point y e X is a Nash equilibrium in the game (1) if and only if y e Argmin max ^(x, y) and max ^(x, ^y) = 0.
y e X x e X x e X
From theorem equivalent optimization problem for Nash equilibrium problem (1) immediately follows:
P ( y ) = max T ( x , y ) ^ min. (2)
x e X y e X
The function P is nonconvex in general case; therefore, search of equilibrium in original game is reduced to search of a global minimum of P . Problem (2) was introduced in [9] and [10] for mixed extension of bimatrix games and then used, for example, in [2; 3]. In [4] the statement (2) is used for computing equilibrium points as well. Reduction of polymatrix games to optimization problem of form (2) was discussed in [11]. In these papers the inner problem in (2) (maximization ^ in x ) can be solved analytically, i. e. we can get an explicit form of the function P .
Another example of equilibrium problems, which admit reducing to optimization problem with explicit objective function, represents the so-called potential games [12]. In this case we also obtain an explicit global optimization problem. Investigations of potential equilibrium problems in the frame of the Cournot model with nonconvexities were performed in [13; 14]. In [15] it was pointed out that in the general case one can use auxiliary support nonlinear functions, which always are available in explicit forms. Within such approach implicit problem (2) is approximated by a sequence of auxiliary (still nonconvex) explicit problems. More detailed description of noncon-vex optimization with nonlinear support functions is given in [16].
Note that equivalence of reduction of game (1) to problem (2) is correct only for games, where each player’s strategy set is independent of other players’ choices. In games with coupled strategy sets, Nash equilibria might exist, which are not solutions for (2) (see example 7 in [8]). However, such kind of games is not in the scope of our present examination.
By definition, P (y) > 0 for any y e X . Hence, if inequality min P (y) > 0 y e X X holds, it means that game (1) has no Nash equilibrium points. On the other hand, the set of global minimizers for P, where P equals to zero, coincides with the set of Nash equilibria for (1).
Denote
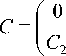
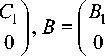
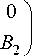
, d =
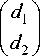
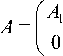
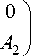
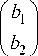
Then problem (2) for the game (1) has the form
P (y) = yT (Cy + d) + 2 yTBy +
+ max - xT ( Cy + d ) — xTBx ^ min, x e X L 2 J y e X
where X = | x e Rm | Ax < b j and m = m 1 + m 2 .
Now we claim for strict convexity of players’ loss functions F 1 and F 2 on X 1 and X 2 respectively. It is equivalent to the condition that matrices B 1 and B 2 are positive definite. From positive definiteness of B 1 and B 2 immediately follows positive definiteness of matrix B . In other words, our assumption implies strict concavity of “inner” maximization problem in (3):
ф(x) = -xT (Cy + d)-2
xT Bx ^ max xe X for some fixed y e X.
Moreover, taking into account non-emptiness, compactness, and convexity of strategy spaces X 1 and X 2 one can conclude that equilibrium point of game (1) always exists due to Kakutani’s fixed point theorem. It means that min P ( y ) = 0 .
y e X
Since ^ is strictly concave function and set X is defined by linear constraints, we have max ф(x) = min max L(x, X) for any y e X, xeX X>0 xeRm
where X e R q is a vector of Lagrange multipliers, q = q 1 + q 2 , and
L ( x , X ) = - xT ( Cy + d ) - — xT Bx -X T ( Ax - b )
is Lagrange function. Obviously, L attains its maximum over Rm in the point, where the first derivative with respect to variable x equals to zero. Then in view of nonsingularity of matrix B , which is ensured by its positive definiteness, we have x * = - B - 1 ( Cy + d + A T X ) such as
max ф ( x ) = min L ( x * , X ) for any y e X .
x e X X>0
Executing substitution, we get:
L ( x * , X ) = -( Cy + d ) T B "1 ( Cy + d ) +
+ ( Cy + d ) T B "1 A T X + 1 X T AB "1 A T X + X Tb .
Then equalities (4) and (5) imply
1 TT -1
max ф(x) = — (Cy + d) B (Cy + d) +
x e X 2 X
+ min ( Cy + d ) T B "1 A T X + - X T AB "1 A T X + X Tb x>0 v ’ 2
Vy e X.
With respect to (6) the problem (3) may be rewritten as
P ( y ) = g ( y ) - h ( y ) ^ min, y e X
where
g(y) = yT |C + 2 B + 2 CTB-1 C^ y + + yT (CTB4d + d) + - dTB~1 d, h (y) = - min v( y, X), X>0 x
y ( y , X ) = X T AB "1 Cy + - X T AB "1 AT X + + X T ( b + AB - 1 d ) .
Next, we formulate the statement that allows us to proceed to numerical method for solving (7).
Statement . Functions g and h are convex.
Proof . Using the symmetry of matrix B and denoting z = ( B + C ) y , quadratic part of g can be easily represented as
T I 1 1 tT -1/"’ 1
y C н— B н— C B C y =
( 2 2 J
= 2 yT (B + C)T B-1 (B + C) y = 2 zTB-1 z.
Since B is positive definite, then zTB - 1 z > 0 for any non-zero z and z ( y ) T B - 1 z ( y ) > 0 for any y . Hence, g is convex. Function ^ is linear with respect to y then h is convex too.
Thus, we represent P as a difference of two convex functions (d.c-decomposition). Our further suggestion is to use for solving problem (7) the well-known iterative local search d.c. algorithm [17]. Its main idea is a linearization of concave term of objective in current iteration point and solving derived convex optimization problem. In such a way, original nonconvex problem reduces to series of convex problems. Next, we describe the steps of that algorithm as it applies to (7). The main difficulty lies in implicit definiteness of objective function. However, we can realize linearization of concave implicit term using the fact that ^ is linear with respect to variable y . In this case, linearization naturally arises.
Algorithm .
Step 0. Set k = 0. Choose numbers s 1 > 0, e 2 > 0 and initial point yk e X .
Step 1 . Get X k + 1 as a solution of convex minimization problem:
X k + 1 = arg min ш ( yk , x ) .
X>0 V /
Step 2 . Get yk + 1 as a solution of convex linearized problem:
yk + 1 = argmin [ g ( y ) + ш ( y , X k + 1 ) ] .
Step 3
. If
P
(
yk
+
1)
1
then STOP:
yk
+
1 is a global solution for (7) and is a Nash equilibrium for (1). Else if
||yk
+
1
-
yk
|| < e2
then STOP:
yk
+
1 is a local solution and is not an equilibrium for (1). Otherwise, set
k
=
k
+
1 and go to the step 1.
Next, we place a simple numerical example with demonstration of algorithm’s iterations.
Illustrative example. Let us consider example of bilinear game with scalar variables of each player, and loss functions F 1 ( x 1 , x 2 ) = 5 x 1 x 2 + 0.5 x 1 2, and F 2 ( x 1 , x 2 ) =
=- 6 x 1 x 2 + 0.5 x 2 . Strategy sets are similar for each player, and represent closed intervals X 1 = X 2 = = [ - 10, 10]. Therefore, parameters of the problem are as follows:
C =
I 0 511-6 0J
, B =
1 0 1 1 1 - 10 0
d =, A =
( 0 J ( 001 - 1
b = ( 10 10 10 10 ) T .
Substitution to (8) gives us g ( y ) = 18.5 y 2 + 13 y 2 - y 1 y 2 , and
( 0 5 )
v( y, X) = X T
( 1
-1
+1XT
-1
V 0
-6
-5
y +
V 6 0 J
-1
-1
X + X T
(10 '
V10 J
Following the steps of the algorithm from initial point y 0 = (10, 10), we obtain results, which are placed to the tab. 1. Here k denotes a number of iteration, X* is a vector of Lagrange multipliers that solves optimization problem on the step 1 of the algorithm, ( y 1 , y 2) is a current iteration point that solves problem on the step 2, and P is an objective value for (7) in current iteration point. It is easy to see, that the algorithm finishes its work in equilibrium point y* = (0, 0).
Computational experiment. In the final part of our paper, we present computational results based on randomly generated problems. For all the problems we set the following general presumptions: players have the same number of variables, i. e. m 1 = m 2 = m / 2 , and set X has the form
X = | x e Rm | - 10 < x i < 10, i = 1, ..., m ) .
Also we set s 1 = s 2 = 10 - 4. Local search algorithm was joined with multistart with randomly generated initial points from X . Program was composed in GAMS [18]. Quadratic convex optimization problems on steps 1 and 2
were handled by CPLEX solver. Also note, that steps 1 and 2 of the algorithm were parallelized by standard GAMS grid facilities with respect to multistart. Experiment was conducted on the PC with AMD FX-8350 4.00 GHz CPU.
Results are gathered in the tab. 2, where every row corresponds to a single particular problem. Notation in the tab. 1 is as follows: MS – number of algorithm’s starts; I aver – average number of iterations for single algorithm’s start; NE – number of starts gained Nash equilibria (where objective P equals to zero); LOC - number of starts, which gives “non-equilibrium” local minima (where objective P has strictly positive value); NEun i q -number of unique Nash equilibria obtained by the multistart; LOC uniq – number of unique “non-equilibrium” local minima obtained by the multistart; Time – overall time spent for all starts for one problem (h:min:sec).
Conclusions. Present paper gives an approach for finding Nash equilibria in bilinear two-person game with strictly convex players’ losses using versatile Nikaido– Isoda function and local search based on d.c-decompo-sition of objective function. Moreover, it is not difficult to see that such an approach can be generalized to games with an arbitrary number of players (see also [2; 7]).
Computational experiment with several random problems shows that proposed local search algorithm in combination with multistart allows finding more than one unique equilibrium point. The time of computation considerably depends on the given problem’s parameters as well as on chosen initial point. At this time, the algorithm is capable to handle only small dimension games and it is in need of further improving. Finally should be noted that, of course, there is no guarantee that local search necessarily gain at least one equilibrium. The task of such a kind needs global search techniques.
Table 1
Iterations of the algorithm
|
k |
^* |
( y 1 , y 2 ) |
P |
|
1 |
(0, 40.00, 50.00, 0) |
(8.32, 8.01) |
900.05 |
|
2 |
(0, 30.06, 39.95, 0) |
(6.64, 6.04) |
700.30 |
|
3 |
(0, 20.18, 29.85, 0) |
(4.95, 4.07) |
500.72 |
|
4 |
(0, 10.36, 19.70, 0) |
(3.25, 2.12) |
301.29 |
|
5 |
(0, 0.59, 9.51, 0) |
(1.55, 0.17) |
101.99 |
|
6 |
(0, 0, 0,0) |
(0.00, 0.00) |
0.00 |
Table 2
Computational results
|
m |
MS |
I aver |
NE |
LOC |
NE uniq |
LOC uniq |
Time |
|
2 |
20 |
1 |
20 |
0 |
1 |
– |
0:00:02 |
|
2 |
40 |
2 |
40 |
0 |
1 |
– |
0:00:08 |
|
4 |
10 |
14 |
10 |
0 |
1 |
– |
0:00:40 |
|
4 |
10 |
4 |
10 |
0 |
1 |
– |
0:00:05 |
|
4 |
20 |
8 |
20 |
0 |
1 |
– |
0:00:19 |
|
4 |
40 |
18 |
36 |
4 |
1 |
2 |
0:01:24 |
|
6 |
10 |
18 |
10 |
0 |
1 |
– |
0:00:30 |
|
6 |
10 |
864 |
10 |
0 |
2 |
– |
0:31:58 |
|
6 |
10 |
102 |
10 |
0 |
3 |
– |
0:03:50 |
|
6 |
10 |
6 |
9 |
1 |
1 |
1 |
0:00:14 |
|
6 |
20 |
214 |
20 |
0 |
1 |
– |
0:08:34 |
|
8 |
5 |
425 |
5 |
0 |
3 |
– |
0:10:48 |
|
8 |
10 |
522 |
6 |
4 |
3 |
3 |
0:04:23 |
|
8 |
10 |
266 |
2 |
8 |
1 |
2 |
0:02:55 |
End tab. 2
|
m |
MS |
I aver |
NE |
LOC |
NF -uniq |
LOC uniq |
Time |
|
8 |
10 |
814 |
10 |
0 |
1 |
– |
0:07:04 |
|
10 |
5 |
188 |
1 |
4 |
1 |
2 |
0:04:32 |
|
10 |
10 |
391 |
7 |
3 |
4 |
2 |
0:15:13 |
|
10 |
10 |
3521 |
2 |
8 |
1 |
3 |
1:29:08 |
|
12 |
5 |
1090 |
3 |
2 |
1 |
2 |
0:41:47 |
|
12 |
10 |
1053 |
5 |
5 |
2 |
5 |
0:44:12 |
|
14 |
5 |
4088 |
1 |
4 |
1 |
2 |
2:05:48 |
|
16 |
5 |
516 |
3 |
2 |
3 |
2 |
0:11:20 |
|
18 |
10 |
1293 |
2 |
8 |
2 |
6 |
0:48:43 |
|
20 |
15 |
3013 |
13 |
2 |
3 |
1 |
1:11:01 |
Acknowledgements. This work was supported by the RFBR (grant ^ 15-07-08986).
Список литературы Local search in bilinear two-person game
- Antipin A. S. Gradientnyy i ekstragradientnyy podkhody v bilineynom ravnovesnom programmirovanii . Moscow, VTs im. A. A. Dorodnitsyna RAN Publ., 2002, 130 p.
- Garg J., Jiang A. X., Mehta R. Bilinear Games: Polynomial Time Algorithms for Rank Based Subclasses. Lecture Notes in Computer Science. Internet and Network Economics, 2011, Vol. 7090, P. 399-407. DOI: 10.1007/978-3-642-25510-6_35.
- Strekalovskiy A. S., Orlov A. V. Bimatrichnye igry i bilineynoe programmirovanie . Moscow, Fizmatlit Publ., 2007, 224 p.
- Gol’shteyn E. G., Malkov U. Kh., Sokolov N. A. . Ekonomika i matematicheskie metody, 2013, Vol. 49, No. 4, P. 94-104 (In Russ.).
- Gol’shteyn E. G. . Ekonomika i matematicheskie metody, 2014, Vol. 50, No. 1, P. 110-116 (In Russ.).
- Quint T., Shubik M. A Theorem on the Number of Nash Equilibriua in a Bimatrix Game. International Journal of Game Theory, 1997, Vol. 26, P. 353-359. DOI: DOI: 10.1007/BF01263276
- Nikaidô H., Isoda K. Note on Noncooperative Convex Games. Pacific Journal of Mathematics, 1955, Vol. 5, No. 5, P. 807-815. DOI: DOI: 10.2140/pjm.1955.5.807
- Flåm S. D., Ruszczyński A. Finding Normalized Equilibrium in Convex-Concave Games. International Game Theory Review, 2008, Vol. 10, No. 1, P. 37-51. DOI: DOI: 10.1142/S0219198908001765
- Mills H. Equilibrium Points in Finite Games. Journal of the Society for Industrial and Applied Mathematics, 1960, Vol. 8, No. 2, P. 397-402. DOI: DOI: 10.1137/0108026
- Mangasarian O. L. Equilibrium points of bimatrix games. Journal of the Society for Industrial and Applied Mathematics, 1964, Vol. 12, P. 778-780. DOI: DOI: 10.1137/0112064
- Strekalovskii A. S., Enkhbat R. Polymatrix Games and Optimization Problems. Automation and Remote Control, 2014, Vol. 75, No. 4, P. 632-645. DOI: DOI: 10.1134/S0005117914040043
- Monderer D., Shapley L. S. Potential Games. Games and Economic Behavior, 1996, Vol. 14, No. 1, P. 124-143. DOI: DOI: 10.1006/game.1996.0044
- Minarchenko I. M. . Diskretnyy analiz i issledovanie operatsiy, 2014, Vol. 21, No. 5, P. 40-53 (In Russ.).
- Minarchenko I. M. . Izvestiya IGU Seriya matematika, 2014, Vol. 10, P. 62-75 (In Russ.).
- Khamisov O. V. A global optimization approach to solving equilibrium programming problems. Series on Computers and Operations Research, 2003, Vol. 1. Optimization and Optimal Control, P. 155-164.
- Khamisov O. V. . Trudy IMM UrO RAN, 2013, Vol. 19, No. 2, P. 295-306 (In Russ.).
- Pham D. T., Le T. H. A. Convex Analysis Approach to D.C. Programming: Theory, Algorithms and Applications. Acta Mathematica Vietnamica, 1997, Vol. 22, No. 1, P. 289-355.
- Rosenthal R. E. GAMS -A user’s guide. Available at: http://www.gams.com/help/topic/gams.doc/userguides/GAMSUsersGuide.pdf (accessed 16.02.2016).
- Антипин А. С. Градиентный и экстраградиентный подходы в билинейном равновесном программировании. М.: ВЦ им. А. А. Дородницына РАН, 2002. 130 с.
- Garg J., Jiang A. X., Mehta R. Bilinear games: Polynomial time algorithms for rank based subclasses//Lecture Notes in Computer Science. Internet and Network Economics. 2011. Vol. 7090. P. 399-407.
- Стрекаловский А. С., Орлов А. В. Биматричные игры и билинейное программирование. М.: ФИЗМАТ-ЛИТ, 2007. 224 с.
- Гольштейн Е. Г., Малков У. Х., Соколов Н. А. Об одном численном методе решения биматричных игр//Экономика и математические методы. 2013. T. 49, № 4. C. 94-104.
- Гольштейн Е. Г. Приближённый метод решения конечной игры трёх лиц//Экономика и математические методы, 2014. Т. 50, № 1. С. 110-116.
- Quint T., Shubik M. A Theorem on the number of Nash equilibriua in a bimatrix game//International Journal of Game Theory. 1997. Vol. 26. P. 353-359.
- Nikaidô H., Isoda K. Note on noncooperative convex games//Pacific Journal of Mathematics. 1955. Vol. 5, № 5. P. 807-815.
- Flåm S. D., Ruszczyński A. Finding normalized equilibrium in convex-concave games//International Game Theory Review. 2008. Vol. 10, № 1. P. 37-51.
- Mills H. Equilibrium points in finite games//Journal of the Society for Industrial and Applied Mathematics. 1960. Vol. 8, № 2. P. 397-402.
- Mangasarian O. L. Equilibrium points of bimatrix games//Journal of the Society for Industrial and Applied Mathematics. 1964. Vol. 12. P. 778-780.
- Strekalovskii A. S., Enkhbat R. Polymatrix games and optimization problems//Automation and Remote Control. 2014. Vol. 75, № 4. P. 632-645.
- Monderer D., Shapley L. S. Potential games//Games and Economic Behavior. 1996. № 14. P. 124-143.
- Минарченко И. М. Численный поиск равновесия в модели Курно с S-образными функциями издержек//Дискретный анализ и исследование операций. 2014. T. 21, № 5. C. 40-53.
- Минарченко И. М. Применение метода ветвей и границ для поиска равновесия в потенциальной модели Курно//Известия Иркутского государственного университета. Сер. «Математика». 2014. Т. 10. С. 62-75.
- Khamisov O. V. A global optimization approach to solving equilibrium programming problems//Series on Computers and Operations Research. Vol. 1. Optimization and Optimal Control. 2003. P. 155-164.
- Хамисов О. В. Невыпуклая оптимизация с нелинейными опорными функциями//Труды ИММ УрО РАН. 2013. Т. 19, № 2. С. 295-306.
- Pham D. T., Le T. H. A. Convex analysis approach to d.c-programming: Theory, algorithms and applications//Acta Mathematica Vietnamica. 1997. Vol. 22, № 1. P. 289-355.
- Rosenthal R. E. GAMS -A user’s guide . URL: http://www.gams.com/help/topic/gams.doc/userguides/GAMSUsersGuide.pdf (дата обращения: 16.02.2016).


