Locating all the Frequency Hopping Components Using Multi-species Particle Swarm Optimization

Published Online August 2011 in MECS

• I．    Introduction

Frequency Hopping (FH) systems have been widely used due to the inherent security features, such as low probability of interception and detection, good capability against interference and hostile jamming in military communications. As the precondition of interception and interference, estimation and tracking the parameters of unknown FH signals are important tasks for information interception and radio sensing with applications in both military and civilian fields. It has become a great challenging problem as the random characteristics of hopping frequency and high levels of noise and interference. To overcome this problem, researches have made many efforts and proposed all kinds of ways for estimating the time and frequency parameters of FH signals [1]-[3].

Because FH signals are typical non-stationary signals, the frequency domain characteristics at any time of signals are important, so it is essential to describe the joint time frequency (TF) characteristics of FH signals. Research on parameter estimation of FH signals by using time-frequency analysis has been carried out for at least two decades. In these literatures, two philosophies for approaching the parameter estimation problem exist-an adaptive component decomposition approach and kernel design approach. FH signals that consist of various TF structures are represents as a combination of components in the former type, which give important information about inner structures. These components could be obtained by using the matching pursuit algorithm commonly [4]-[6]. But these methods require building parametric, redundant, and well-localized TF atoms, which are matched with FH components difficultly, and high computational time is also a huge bottleneck. In the latter type, FH signals is described generally by a function with time and frequency variables and parameter estimation is operated on the TF plane. Barbarossa [7] proposed a method for estimating hop parameters based on Pseudo Wigner-Ville Distribution (PWVD). There are also cross-terms along frequency axis, but they can often reduced by a two dimensional low-pass filtering of WVD, leading to the smoothed PWVD so that the estimation of hop during parameter is reliable above 4dB [8], [9]. However, the SPWVD reduces time and frequency resolution while decreasing interference items, where assuming hop during is known in that algorithm. In order to improve the readability and resolution of TF distribution, Auger and Flandrin proposed a reassignment method [10]. The method reallocates the energy value of arbitrary point in the original TF plane to the center of gravity of these energy contributions, which is applied to parameter estimation by [11]. Image processing techniques are also applied in this problem in [12]. Nevertheless, TF resolution in the above methods is always losing with the reduction of interferences, where the locations of the maximal values of TF distributions appear shift. On the other hand, hop timing can’t be correctly estimated using maximum sequence as itself may be wrong and the resulting hop frequency is also a mistake, especially in low SNR noise, although difference operation is simple.

Based on the above analysis, we can see that all the introduced methods must estimate the maximum along time domain or frequency one. This operation is sensitive to noise due to differential operator. In this paper, we propose a new parameter estimation algorithm based on PSO. The proposed estimator utilizes particle search to search peaks in TF plane so as to obtain time and frequency parameter of FH signals simultaneously. Experiments results illustrate that it can be performed effectively of the proposed algorithm in strong noise environment without any prior knowledge.

This paper is organized as follows. The next section consists of a brief review of PSO and Multi-Species PSO (MSPSO). Then we introduce FH signal model into PSO and give the problem formulation. In section 4, the new peaks i.e. FH components search algorithm is proposed, whose performance is evaluated and hop during estimation method is also discussed in Section 5. Finally, Section 6 summarizes the conclusions obtained from this research work.

• II．    Multi-Species Particle Swarm Optimizer

  Inspiring from the swarms in nature, in 1995, Kennedy, Eberhart and Shi [13] proposed a new heuristic method called PSO based on sociological behavior associated with birds flocking. PSO combines cognition only model that values solely the self-experience and social only model that values solely the experience of neighbors. In particle swarm optimizer, each particle, which represents a potential solution to a problem at hand, adjusts its flying according to its own flying experience and its companions’ flying experience. Each particle is treated as a point in a D-dimensional space. The i^th particle is represented as X , = ( x^, x^ , l x_iD ) . The best previous position giving the best fitness value of any particle is recorded and represented as P , = ( p 1 , p_{i 1}, L p_iD ) .The best particle among all the particles in the populations is represented by the symbol g. The velocity for particle i is represented as V, = ( v_n,v_n,---v_iD ) . The particles are manipulated according to the following equation:

v d ⁽ t + 1) = wv d ^{( t} ) ⁺ c l r ld ^{( t )( P} d ^{( t} ) - x d ⁽ t )) + c 2 ^r 2 d ^{( t )(} P d ^{( t} ) - X d ⁽ t )) ^(1a)

x id ⁽ t ^{+ 1)} = x d ⁽ t ) ⁺ v d ⁽ t ^{+ 1)}

where w is the inertia weight factor; c1 and c2 are cognitive and social acceleration factors, respectively. c1 and c2 are uniformly random numbers chosen from the interval [0, 1]. Here, PSO is designed to locate a unique single optimum solution. However, algorithms to find more than one optimum of a function, usually referred to as a multimodal function optimization, have been widely studied since it exists in engineering fields, for example, in this paper [14]-[18]. Previous approaches can be categorized as iterative and subpopulation methods. Parsopoulos and Vrahatis [14] introduced the unified PSO, which requires local and global neighborhoods to be defined aiming their balance. Li proposed [15] the species-based PSO. This method gathers the similar particles into species, which is defined by two variables: species seed and species radius. The particles in the entire swarm move and converge around those seeds, which parameters denote the locations of multimodal values. Unfortunately, a cumbersome genetic schedule is necessary to tune the performance of the algorithm [16]. Masao [17], [18] divides the whole population into several subpopulations called species directly. Each species Ps occupies a different area of the search space and tries to find out the local minima of that area. Therefore, it can be used to locate all the global minima of the multi-modal function in parallel. If the distance between particle i and species seed s at Ps is shorter than the threshold c called species radius, then i belongs to species s. In general, the Euclidean distance is used, while it is modified according to the application in this paper and illustrated in the following. Now in MultiSpecies PSO (MSPSO), a global best position Pg is replaced by the species best Ps that is the best position of the species to which the particle i belongs and (1a) of PSO is replaced by:

v d ( t ^{+ 1)} = wv d ( t ) + c l r ld ( t ^{)( P} d ^{( t} ) - x d ⁽ t )) + ^C 2 r 2 d ⁽ t ^{)( P} sd ^{( t} ) - x d ⁽ t )) ⁽²⁾

• III．    signal model and problem formulation

• A.    Signal Modal

The FH signal is modeled as TF shift result of a single tone x ₀ ( t ), i.e. consists of some components:

x(t ) = ^ xft ) = ^ x 0 (t - t_z .)cos(2 n ft +ф ) + n ( t )   0 < t <  T   (3)

where x 0 ( t ) = rect H ( t - T h - а Т н ) cos(2f , rect_Th ( t ) is equal to one for t e [ - T h -, T h -] and zeros elsewhere. f is the generic hop frequency, T_H is the hop duration, a T_H is the hop timing, ф is the initial phase of each hop, n(t) is additive noise. T_H , f i and a T_H is the parameter sets to be estimated. Here, x_i is called FH components, which is denoted by two variables: time t_i and f_i . In fact, FH parameters, such as hop during, hop timing and hop frequency are estimated by the parameter sets { t_i , f_i }.

• B.    T me Frequency Analys s

The WVD of a signal s (t) is defined as follows:

W_f ( t , s ) = J I s ( t + 2 ) s *( t - 2 )e 2 "ч1 т        (4)

Then, we can write the WVD of the FH signals x(t) as

W x (t , f) = 1^ , f) + 2 n -i £^( < - t mkl , f - fkd ) x cos[2 n f k ( t - t mk ) z-x i = 1                  k = 1 l = k + 1                                                         ⁽^ )

• - t dk ^{( f} - Л « ) ^{+ 2 П} / dll t mkd ^]

where (tdkl, fkH ) = (4 - tl, fk - fl ) corresponds to the difference in the time and frequency shifts and (tmkl, fmkl ) = (4 + tl )/2,( fk + fl )/2] is the average TF shifts between two components about FH signals. Wx (t,f) is WVD of the arbitrary of “base” signalx0(t), sin[4n(f - f ))TTH -|t|)]

Wx,. ( t , f ) = n ( ^f - ^f ' )

x 0            0

| t <  T h

I t >  ^T H

and W_x ( t , f ) is the WVD of the component signal x_i ( t ) as

W ( t , f ) = J -I x ( t + f) x ( t - 2) e -^{j2 n f l} dr = W x ( t - t , f - f ) (7)

In the above equation (5), the n terms in the first sum corresponds to the auto-components W_x ( t , f ), which it is clear that W_x ( t , f )is centered along the time t and frequency f for any component, whereas the last sets of terms are the cross terms, which are located at the average time t_mkl and frequency f_mkl . It can be seen that the cross terms are oscillatory in nature and could be removed from TF plane by smoothing or filtering, for example, SPWVD [19]. Fig.1 (a) gives the maximum sequence plot of SPWVD which shows peak domains including seven hop components using difference operator. However, we can hardly find the location of these maximums due to the existence of the noise and the interference, for example in SNR -2dB, shown in fig.1 (b). Thus, the hop timing, hop during and hop frequency consequently is not estimated correctly as in previous literatures.

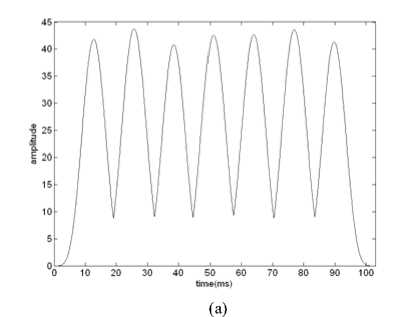
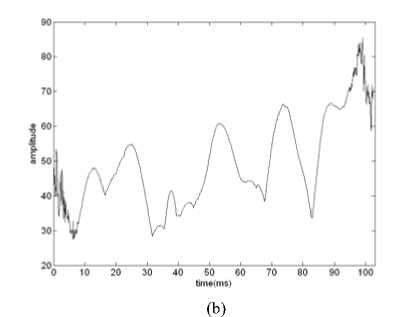
Fig. 1: The maximum sequence of SPWVD. (a) without noise. (b) SNR=-2dB

C.Problem Formulation

Our objective is to estimate hop instants and hop frequencies of the transmitted signals from noise signal x(t). From above analysis, the maximum locations on TF distribution represent the TF center of all components, which values is sensitive to noise. In this paper, we look peaks search problem upon as multi-modal function optimization and use MSPSO algorithm to locate the maximums so as to obtain the TF locations of all components which use to estimate parameters of FH signals.

The particle is a candidate solution of evaluating TF parameters, which is represented by a 2-dimensional realvalued vector, i.e. (Pi 1,p2) = (t, f) .A certain number of particles form a species population and as particles moves through the search space, it compares its objective function with the best that it has ever attained so far. The behavior is repeated until all particles are gathered around the species seed of each species according to the distance measure, or a maximum iteration is encountered. With reference to (7), TF distribution (5) is chosen as the objective function in this study. The parameter estimation of signal (3) can be achieved by searching suitable Psd, d = 1,2 such that the objective function is maximized, i.e.

⁽ t *,^f * ) = arg ( m mW ⁽ t , ^f )              (8)

where S is search space which admitted for subpopulations.

• IV．    Estimation Algorithm

Given a sequence of samples x(n) of the observed signal, with n = 0,1, l N and N is the sample numbers, the estimation algorithm is based on the following steps:

• 1)    Compute the discrete SPWVD of the signal x(n).

• 2)    Generate an initial random population with initial locations and velocities containing H particles chosen from the interval [1, N]. The initial personal best location is set by its current position.

• 3)    Given species radius, each particle i moves around the search space, and changes its velocity according to (2) and position as (1b).

• 4)    Find a new species seed s of assigning particle i to appropriate species s using MSPSO algorithm in (8). For a single FH signals, there are not overlap in time domain,so the distance measure is defined by the following equation

d (i, s) = |xz. 1 - Xi 1|               (9)

• 5)    If the pre-specified number of iterations is not achieved or not all particles are gathered, go back to steps 3.

• 6)    Output the species seeds, i.e. time and frequency center of all obtained FH signal components.

In this algorithm, neither the number of species nor the population of each species is pre-determined [17], so the number and parameters of FH components are blind estimated.

V ． Simulation studies

The performance of the method has been evaluated by simulation in the presence of additive white Gaussian noise using the packet software of MATLAB 7.0. An example is useful to illustrate the estimating procedure. The hop frequency alphabet is {1.5 kHz, 1.75 kHz, 2.0 kHz, 2.25 kHz, 2.5 kHz, 2.75 kHz, and 3.0 kHz}. The sample rate is 10 kHz. The hop during is 12.8ms.

Figure 2 shows the evolution of clusters of a species in a particle swarm when the whole population is 500, the maximum velocity is twenty percent of the variable range, species radius is 65, and the maximum number of iteration is 300. The horizontal axis corresponds to time while the vertical one represents normalized frequency. During the evolution of population, each particle moves around the search space and immigrate from one species to another until the whole population is partitioned into different species, which the number of species is the number of signal components, i.e. 7. The trajectory of a particle can be guaranteed to converge if the parameters of PSO are chosen so that the corresponding particle’s location always falls in the convergent region as shown in Fig.2 (ac). For the two acceleration coefficients and the inertia weight, we set the standard values 2.05, 0.8, respectively as in [18].

V

100 F

0 I____L?_______I—•_____ «I _e I • _______* M____I___________•_____I________®J I

0    100   200   300   400   500   600   700   800   900  1000

(a)

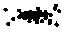
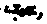
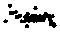
250 [-----------------1-----------------1------------------1-----------------1------------------1-----------------(-----------------1------------------(-----------------1------------------1

0    100   200   300   400   500   600   700   800   900   1000

(b)

650 [------------------r------------------r------------------r------------------1------------------1------------------1------------------1------------------1

400 Г1

350 Г            *1

300 I_______________(_______________i_______________i_______________I_______________I_______________I_________*___II

100    200    300    400    500    600    700    800900

(c)

Fig.2: The evolution of the swarm population in TF plane. The dots indicate the locations of the particles, and the red crosses indicate the positions of component center. (a) iter=0. (b) iter=10. (c) iter=50.

The performance of this method has been evaluated by simulation in the presence of additive white Gaussian noise. The proposed algorithm was tested for 30 independent runs (trials). In each run, the same parameter as extracted above was used. Table 1 presents the time and frequency location of all the seven components in different SNR. The units in Table 1 are time or frequency sample. We can observe, as expected, the estimated parameter values are similar to the true one below 0dB, which the absolute error is less than 3 samples.

Table I the estimated parameter values of FH components

Component index	SNR=-2dB
	time	frequency
#1	128.2616	562.1197
#2	256.2342	358.0306
#3	381.0979	460.2252
#4	517.2211	611.8515
#5	645.4963	511.8684
#6	765.3898	308.1621
#7	898.6748	408.1488

TABLE II.

the estimated parameter values of FH components

Component index	SNR=0dB
	time	frequency
#1	127.5250	562.3153
#2	256.0044	357.8336
#3	382.2852	460.0340
#4	515.2323	612.9383
#5	643.4909	511.3633
#6	766.4841	307.2144
#7	899.0985	408.4468

TABLE III.

the estimated parameter values of FH components

Component index	SNR=2dB
	time	frequency
#1	128.0765	561.7338
#2	256.6829	357.2694
#3	385.0712	460.2256
#4	511.4474	613.7101
#5	640.4656	510.8083
#6	770.2921	306.3655
#7	897.5453	407.5886

A simplified explanation of the above algorithm is designed for hop during estimation, which is obtained by computing the average for the difference of all the seeds taking account of time variable. The mean –square error of this parameter estimation at different SNR values in the range of -10dB to 2dB is shown in Fig.3 using the proposed method and the algorithm in [7]. It can be seen from Fig.3 that the modified MSPSO algorithm using our approach can be used to estimate parameter of FH signals. This algorithm achieves several goals comparing with [9]. First, optimization search approach is reliable, i.e. no mutations of performance, in a wider range of SNR, since there is not a threshold effect, although lower variance is obtained using SPWVD above the SNR threshold. A second benefit of this approach is that there is no error propagation phenomenon because time and frequency variables are independent. Finally, another benefit of our method is the ability to estimation parameter correctly in the very low SNR noise, which is in accordance with component location estimation formerly.

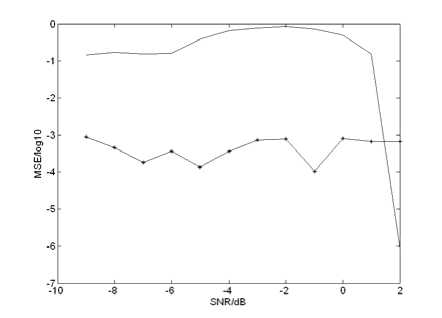
Fig.3 hop during estimation variance

• VI．    Conclusions

By applying the proposed PSO optimization for TF distribution, blind parameter estimation of frequency hopping signal is solved taking account of the relation between peaks location on the TF plane and component centers of frequency hopping signals. Differently from other known methods, the proposed method provides a direct search method of time and frequency parameter of FH signals. The experimental results proved that the theoretical derivation is correct and the proposed method is effective and feasible under the low SNR. One future work will include how to unify TF representation and PSO having simple and robust properties, which could give high-precision.

• VII ．    ACKNOWLEDGMENT

  This paper is based upon supported by Natural Science Foundation of Henan Province Educational Committee under Grants No.2011A510021, Scientific Research Foundation for High-level talent, Xinyang Normal University.

Acknowledgment

• [1]    J. J. Lehtomaki, M. Juntti, “Detection of frequency hopping signals using a sweeping channelized radiometer,” Dignal Processing, Vol. 85, pp. 2030-2043, 2005.

• [2]    J. J. Lehtomaki, “Maximum based detection of slow frequency hopping signals,” IEEE Communications Leters, vol. 7, No.5, pp. 201-203, 2003.

• [3]    G. Lopez, O. Y. Ojeda, “Atomic decomposition based complex radar interception,” IEE Proceedings Radar, Sonar and Navigation, pp.323-331, Aug, 2003.

• [4]    S. Mallat and Z. Zhang, “Matching pursuits with timefrequency dictionaries,” IEEE Trans. Signal Processing, vol. 41, pp. 3397–3415, Dec.1993.

• [5]    Ye Yuan, Wen-bo Mei, Si-liang Wu, “Hop Period Estimation for Frequency Hopping Signals Based on Hilbert-Huang Transform,” 2008 Congress on Image and Signal Processing, vol.5, pp.452-455, 2008.

• [6]    Jiantao Guo, “Adaptive time-frequency parameterization of frequency-hopping signals based on evolutionary algorithm,” 2010 Third International Joint Conference on Computer Science and Optimization, vol.1, pp.279-282, 2010.

• [7]    S. Barbarossa, “Parameter estimation of spread spectrum frequency hopping signals using time-frequency distributions,” First IEEE Signal Processing Working on Signal Processing Advances in Wireless Communications, pp. 213-216, 1997.

• [8]    Zhang Chao-yang, Cao Qian-qian, and Chen Wen-zheng, “Bling separation and parameter estimation of multiple frequency-hoppings,” Journal of Zhejiang University (Engineering Science), Vol.39, No.4, pp. 465-470, 2005 (in Chinese).

• [9]    Zhao Jun, Zhang Zhaoyang, Lai Lifeng, “Blind parameter estimation of frequency-hopping signals based on timefrequency analysis,” Journal of circuits and systems, Vol.8, No.3, pp.213-216, 2003 (in Chinese).

• [10]    F.Auger, P. Flandrin, “Improving the readability of time frequency and time-scale representations by the reassignment method”, IEEE Trans. Signal Processing, Vol.43, No.5, pp.1068-1089, 1995.

• [11]    Tian Yan, Gou Yanxin, Chi Wanhong, Bu Weidong, “Reassignment-based frequency hopping signal timefrequency analysis,” Communication Countermeasures, vol.96, No. 1, pp:8-12, 2007.

• [12]    Xu Mankun, Ping Xijian, Li Tianyun, Xu Mantian, “A new time-frequency spectrogram analysis of FH signals by image enhancement and mathematical morphology,” Fourth International Conference on Image and Graphics, ICIG 2007, pp.610-615, 2007.

• [13]    J.Kennedy, R C Eberhart, “Particle Swarm optimization,” in proceedings of IEEE international conference on neural networks, Picataway, NJ, pp.1942-1948, 1993.

• [14]    K. E. Parsopoulos, M. N. Vrahatis, “UPSO: A Unified Particle Swarm Optimization Scheme,” Lecture Series on Comp. and Computational Sci., Vol. 1, Proc. of the Int. Conf. of Computational Methods in Sci. and Eng., pp. 868873, 2004.

• [15]    J.-P. Li, M.E. Balazs, G.T. Parks, P.J. Clarkson, “A Genetic Algorithm using Species Conservationfor Multimodal Function Optimization,” Journal of Evolutionary Computation,vol. 10, no. 3, pp. 207-234, 2003.

• [16]    R. Brits, A.P. Engelbrecht, F. van den Bergh, “A niching particle swarm optimizer,” Proc. 4thAsia-Pacific Conf. on Simulated Evolution and Learning, vol. 2, pp. 692-696, 2002.

• [17]    M Iwamatsu, “Multi-species particle swarm optimizer for multimodal function optimization”, IEICE Trans. INF.&SYST., Vol.E89-D, No.3, pp.1181-1188, 2006.

• [18]    Masao Iwamatsu, “Locating All the Global Minima Using Multi-species Particle Swarm optimizer the inertia weight and the constriction factor variants,” in IEEE Congress on Evolutionary Computation, pp. 16-21, 2006.

• [19]    K Shubha, G.B. Bartels, “A comparison of the existence of “cross terms” in the Wigner Distribution and the squared magnitude of the wavelet transform and the short time foourier transform,” IEEE Transaction on Signal Processing, vol.40, No.10, pp.2498-2517, 1992.

Guo Jiantao received the M.Sc. degree in signal and information processing (optical information encryption) from DaLian University of Science and Technology, Dalian, China and the Ph.D. degree in signal and information processing (time frequency analysis) from Huazhong University of Science and Technology, Wuhan, China, in 2004 and 2009, respectively.

He is an associate professor with the College of Physics and Electronic Engineering, Xinyang Normal University, Xinyang, China. He maintains an active interest in the field of time frequency analysis and swarm intelligence. Further research interests include spread spectrum signal processing, digital watermarking, and blind source separation.

Wang Lin received the B.Sc. degree from the Yunnan University, Kunming, China, in 1985 and subsequently worked in the College of Physics and Electronic Engineering, Xinyang Normal University, Xinyang, China. Her research focuses on frequency-hopping signal processing and evolutionary computation.