Location Privacy using Homomorphic Encryption over Cloud

Published Online August 2017 in MECS DOI: 10.5815/ijcnis.2017.08.05

User location privacy has now become one of the most important security agendas to be discussed and catered to in almost all new as well as older computer applications. And addressing this agenda, Location-Based Services (LBSs) have become the most significant services in this context aware field. Location- based services provide the desired services and data based on the location provided by the user. Although these services make our lives easier, however they also make us highly vulnerable to privacy risks. This is because in order to avail the desired services, a user has to reveal and uncover his location to the server. Thus, it can be rightly stated that his location privacy is threatened.

In the proposed system, “Fig .1”, I wish to build solution for kNN (k- Nearest neighbour) queries using homomorphic properties of Paillier public-key cryptosystem.

• •    The mobile user initiates a request by sending location-based queries to the LBS (Location Based Service) provider. Since this request is encrypted and then sent to the server, therefore his location is not revealed to the server.

• •    The LBS provider carries out various computations and calculations on the encrypted location query provided by the mobile user and this way it furnishes location based services to the user.

• •    The communication gap between the LBS provider and the mobile user is bridged by a base station.

• •    Location based information is provided by satellites.

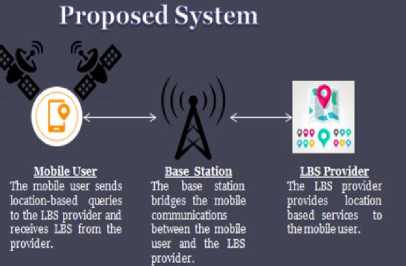
LBS Provider

The LBS provider provides location based services to tiie mobile user.

Base Station

The base station bridges the mobile communications between the mobile user and the LBS provider.

Mobile User

The mobile user sends location-based queries to the LBS provider and receives LBS from the provider.

Fig.1. Proposed System

• II.  Existing approaches

There are many existing approaches and techniques,

Copyright © 2017 MECS

I.J. Computer Network and Information Security, 2017, 8, 32-40

“ Fig. 2”, which may also ensure location privacy. Going through the below section, one can develop a fair picture about these methods and approaches.

• •    Information Access Control [2]

• •    Mix zone [3]

• •    K-anonymity [4], [5]

• •    Dummy locations [8], [9]

• •    Private Information Retrieval (PIR) [8], [9]

• •    Geographic data transformations [8], [10]

All LBS queries that use mix zone [3], access control [2] and k-anonymity [4][5] approach either require a service provider or a middleware that stores all locations of the user. However, since they are storage areas, they are vulnerable to any kind of misbehaviour conducted by a third party, adversary. Thus very little protection is ensured in case the service provider or the middleware is 0wned or maintained by an untrusted party.

• A.    K-Anonymity

K-anonymity was first used for identity privacy protection. LBS queries that are built and based on the concept of k-anonymity are highly dependent on two parameters - the density and distribution- of the mobile users, which, cannot be controlled by the location privacy technique.

• B.    Dummy Locations

In case of LBS queries that are based on “dummy” locations, a set of fake locations is randomly selected by the mobile user and sent to the LBS. The user then receives the false results from the LBS over the mobile network. However, this way both communication as well as computation overhead is incurred in the mobile devices. The mobile user might choose less fake locations for the purpose of efficiency, however the location based service provider can also limit the mobile user in smaller sub spaces of the larger domain, leading to weaker location privacy.

• C.    Geographic Data Transformations

Geographic data transformation [8][10] based LBS queries are susceptible to access pattern attacks since the same query always returns the same results in an encoded format. For instance, the LBS provider may notice the frequencies of the cipher texts and, thus, reveal information about the query .This can be simply done by having knowledge about the database’s context and matching the most frequent plaintext POI with the most frequently returned cipher text.

• D.    Personal Information Retrieval(PIR)

PIR [8][9] based LBS queries are cryptographically stronger, but are often expensive in context of computation and communication. In order to improve efficiency, one can employ trusted hardware to perform personal information retrieval for LBS queries. Like LBS queries that are based on access control, mix zone and k-anonymity, as discussed above, this technique is susceptible and vulnerable to any kind of misbehaviour by an adversary. This is because this mechanism is modelled on hardware-aided PIR. In this model, the system is initialized by a trusted third party (TTP) by setting the permutation of the database and secret key.

Giving PIR based solutions for kNN queries which are practical along with ensuring location privacy was a challenge. However, “Xun Yi, Russell Paulet, Elisa Bertino, and Vijay Varadharajan” [1] gave following main contributions:

• •    Current PIR-based LBS queries [8][9], generally work in two steps. As a first step, the mobile user calculates and finds the index of his location according to the cloaking region (CR) and then as a second step he finds the points of interest (POIs) according to the provided index from the LBS provider. To make the process more comprehensible, they have given a one-step solution for kNN queries in which the mobile user transmits his (encrypted) location to the location based service (LBS) provider and receives the k-nearest (encrypted) POIs from it.

• •    Earlier, the mobile user could only retrieve k nearest POIs irrespective of the type of POIs on using current PIR-based LBS queries [8][9]. For the first and foremost time, they have taken into consideration the type of POIs in kNN queries and given a method to the user to find the k- nearest POIs of the same type without revealing the type of POIs he is interested in to LBS provider. For instance, their solution allows the user to find out k-nearest car parks/hotels/schools from the LBS provider without revealing his location as well as his POI.

• •    Current PIR-based LBS queries [8][9], generally choose a fixed cloaking region ,CR. Later according to the fixed CR and the query provided, the service provider creates a response to these queries. This response is then sent to the mobile user. The LBS queries are inefficient, in case the CR is large. Also, the LBS queries have weak privacy, if the CR is small. Thus they have given a solution where even if the mobile user specifies a large public CR, the LBS provider still creates the results based on a small private CR repeatedly.

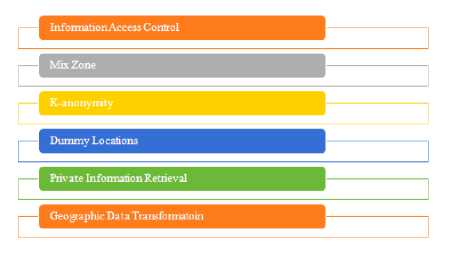
Fig.2. Existing Approaches That May Provide Location Privacy to Some Extent.

• III.    Paillier Cryptoscheme

Paillier cryptoscheme is actually a non-deterministic and probabilistic asymmetric key encryption scheme which uses different pairs of public and private key to encrypt and decrypt any plaintext. Paillier cryptosystem depends on a random element г for encryption per message bit. Also, it involves only one multiplication for each homomorphic addition and one exponentiation for each homomorphic multiplication making it a simple, efficient and better choice.

Key Generation

Randomly choose any two large prime numbers а and b such that gcd(ab,(а-1)(b-1))=1

Calculate п=

Calculate л=     (а-1,b-1)

Choose value of generator 9 , such that 9ℤ

Qcd ( (дх mod п2 - 1)/п,п)=1

Calculate

µ=(L(д2 mod п2 )) - 1 mod и,(5)

where

L ( х )=( х -1)/ п .

This function is only used on input values µ that actually satisfy µ = 1 mod и .

Public Key: (и, д )

Private Key: (Л,µ)

Encryption

Plaintext, where т ∈ ℤ

Randomly select г where г ∈ ℤ^∗

Calculate cipher text as:

с =    ∙ rⁿ mod п²            (6)

Decryption

As implied from equation (6),

Cipher text с ∈ ℤ^∗

Compute message:

т =( с^л mod п² )∙ д mod и         (7)

Paillier Cryptosystem can be illustrated using the following example (1).

Example 1:

Key Generation

Let а = 49727 , b = 56737

п =   = 2821360799

п² = 7960076758133918401

Л=    (а-1, b -1) = 1410627168

Choose a random, д = 1624691728

L = 2197925655

µ = 1779031213

Public Key: (2821360799, 1624691728)

Private Key: (1410627168, 1779031213)

Encryption

Plaintext, т = 1468689009

г = 1489472025

Cipher text с=     ∙            =

(956651757) 1468689009 . (1489472025) 2821360799 mod 7960076758133918401

= 2015851325878209300

Decryption т=(ся mod п2)∙        =

L (20158513258782093001410627168 _той 7960076758133918401).1779031213 mod 2821360799

= 1468689009

Homomorphic Property

Paillier Cryptosystem holds the property of additive homomorphism.

On decryption, the product of two ciphers gives the sum or addition of their respective inputs, i.e. the respective plaintexts.

D ( Е ( т_г , ^ri) ∗ Е ( т₂ , ^Г2)) mod п² =( т_г + т₂ ) mod п

• IV.    System Architecture

The proposed system is built and based on the architecture explained in this section. A schematic view can be obtained from “Fig.3”. It consists of three algorithms as discussed below. The functioning and details of the algorithms will be discussed in Section V (How it works).

• 1)    Query Creation (QC)

Query Creation (QC): Accepting the following as inputs,

• •    a fixed, cloaking region, CR divided into grid of п х п cells ,

• •    the location (x, у) of the mobile user;

The mobile application user generates request to be sent to the server. It consists of a query Q and a secret value, s , denoted as:

( Q , s) = Q C( CR,n,(x,y)).        (8)

• 2)    Response Creation (RC)

Response Creation (RC): Accepting the following as inputs,

• •    the mobile app user’s query Q,

• •    a location-based database containing information about name and distance of P0Is from each cell of the CR;

The LBS provider generates a response R , as a result of the provided query. It is denoted as:

R = R C( Q , D).                 (9)

• 3)    Response Retrieval (RR)

Response Retrieval (RR) : Accepting the following as inputs,

• •    the response value, ,

• •    the secret value, ,of the mobile application user;

The mobile user finally generates к nearest P0Is, which can be denoted as kNN = R R(R ,s).             (10)

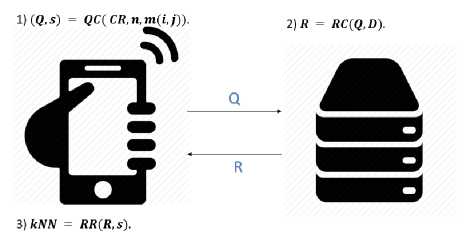
Fig.3. System Architecture

• V. How It Works

“Fig. 4” and “Fig 5” show the working of the proposed system. In this system proposed, the concept of location preservation works efficiently using the following algorithms (in sequence). There is a client (mobile user)

which accesses its location and sends it to the server. The server on its end stores values ( ) of nearest locations in an integer format. For example, cell(1,2) has 2 nearest hotels , cell (2,3) has 0 nearest hotels.

Step 1 :

Fix a Cloaking Region, CR , in which the user queries about a location based service. (Figure 7)

Step 2 :

Divide the CR into square grids, such that each fixed sized cell is of a particular dimension, say 1 x 1 km in my case. (Figure 8)

Step 3 :

Index the square cells into (x, у) format and assign an index to the user’s location. (Figure 9)

Step 4:

Once the locations are assigned an index, the following three algorithms are used to encrypt the location and avail location based services.

• •    The user (client) first generates a key pair (sk, p k) , where is the secret key and is the private key.

• •    The user’s location (x, у) is encrypted using Ericrypt algorithm of Paillier Encryption Scheme.

• •    The user also chooses a place if interest, poi, whose index is also sent to the server along with the encrypted location.

• •    The server applies some calculation on the cipher text sent from the client side using the matrix. This   matrix stores values ( ) of number of

nearest locations to each cell ( , ) in an integer format.

• •    Finally the encoded result (cipher text on which calculation has been performed) is returned to the client.

• •    The user then decrypts the encoded result using the private key (  ) to obtain value of corresponding

to its respective location.

Hence the user comes to know whether or not there exists a hotel nearby. If yes, then how many hotels are actually nearest to the user’s location.

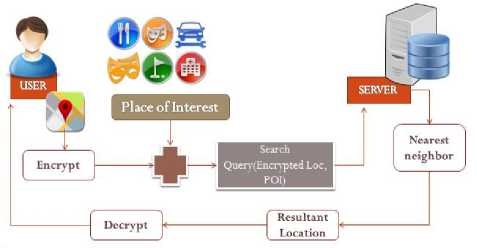
Fig.4. Working of the Proposed System.

Algorithm 1: Query Creation, QC (Mobile APP User)

Input : CR ,n, (x,y)

Output : Q , s

• a)    Randomly pick any two large prime numbers a, b such that N = a. b > N

• b)    Consider secret key, s к = {a, b } , and public key , p к = {g,N{ , where g is chosen from 2 * ₂ and the order of is a nonzero multiple of N.

• c)    Randomly choose an integer r_t E 2 *₂ , for each I E {1,2,3,....n}, and compute

_ Г Encrypt (1, p k) = g ^rr _; ^w (mod N²) if I = x

• ¹   {Encrypt (0, p k) = д^ог^ (mod N²) o thrrwise

Where “ Ппггур t ” is nothing but the encryption algorithm as explained and can be found under Paillier Cryptosystem in Section III.

• d)    User chooses his point of interest, .

• e)    Let Q = { CR ,n,c_r, ........, c_n,po i, pk} , s = s к

• f)    Return { , }

• VI. Design and Implementation

• A. Mobile Application Development

In order to allow a user to access his location, I have first designed an android mobile application.

To include the location tracking capabilities in the application, I have used the Location Manager class.

• •    Location Manager: This class provides access to mobile based location service.

• •    It gives higher accuracy over other available 0ptions.

• •    It is power saving. This is because of the fact that it utilizes comparatively low power by selecting the most efficient method of accessing the user’s location.

• •    Class can be retrieved through.

Context. ge tSystemSerf ice И

( onte xt. L 0 C ATI ON SER VICE ) .

Location Manager Class can be used in two ways to find user locations using NETWORK_PROVIDER and GPS.

Algorithm 2: Response Creation, RC (Server)

Input : D, Q = ^{ CR ,n,Cr, ........,c „ , (g,N)^}

Output : = { C r , C 2 ,....., C_n }

• a)    Compute R = { C _r , C ₂,..... , C „ } , where for

Y = 1,2,.....,n

• b)   C _y = O” = _r c^dz ' ^y(mo d N²)

• c)    Return R

Algorithm 3: Response Retrieval, RR (user)

Input : R = { C _r , C ₂,..... , C _n }, s = s к

Output: d

• a)    Calculate value, d = Decrypt(C _y , sk) , where “ Decryp t ” is the decryption algorithm as explained and can be found under Paillier Cryptosystem in Section III .

• b)    Return value of

dx,y = RR(R,s) , w□ ere dyy s tan ds for к neares t P 0 Is for t □ e ce 11 (x,y), (Q ,s)= Q C(CR,n,(x,y )), R = R C(D,Q ).

Proof. Based on Algorithms 1–3, we have cy = O”= r cd 1 ,j = gdx(nW= rrd 1 ,y) mod N2

Which is nothing but encryption of d _z,_y (Section III). Therefore, we have    d _z,_y = D e cryp t (C _y , sk) =

( ,   ) and hence the theorem is proved.

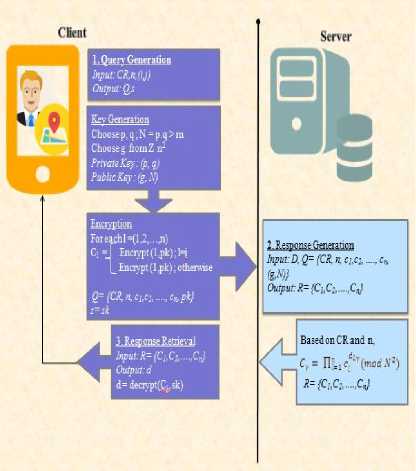
Fig.5. Working of Algorithms.

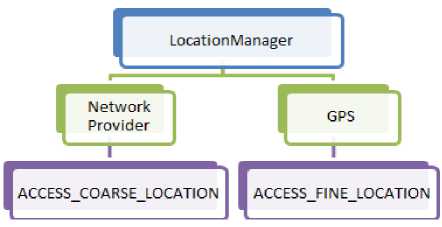
Fig.6. LocationManager Capability for Android App Development

Network Provider

• •    Finds and retrieves the location of the users using Wi-Fi access points, cell towers etc.

• •    Considers the distance between user’s location and the cell tower.

• •    Provides a faster result.

• •    Usually a better choice when trying to access locations from indoors (inside the rooms or buildings).

GPS

• •    Finds and retrieves the location of the users using satellites.

• •    Uses GPS based coordinates which are used for positioning.

• •    The signals from the satellites are receive by the GPS receiver in the smart phones. These signals are then used and processed for determining the exact and precise locations.

• •    Usually takes longer time in sending the response, causing delay in determining the location.

• •    Generally a better choice for determining location in outdoors, since direct sky/satellite views and communication occurs.

Android Permissions

• •    Access_Coarse_Location is used for determining approximate location using cell towers and Wi-Fi access points.

• •    Access_Fine_Location is used for determining precise location using cell towers and Wi-Fi access points.

• •    Internet is use for connecting to the internet and performing network operations using the mobile app.

  I have further divided this map into equal sized cells. It forms a 6x6 grid structure as can be seen in “Fig 8”.

  
  
  

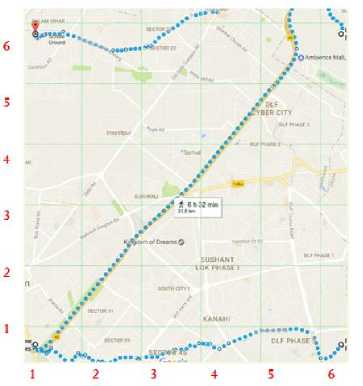
  Fig.8. Cloaking Region Divided Into Grids.

  
  

  C. Mobile App Snapshots

  
  
  

• B. Cloaking Region Division

I have fixed a cloaking region for the proposed system. It looks like,” Fig 7”.

Fig.7. Cloaking Region

• VII.    Findings

The proposed system proved to be secure from various aspects. The following section enlists all kind of findings obtained after implementing the proposed system. Section A gives a fair description on how the system proves to be secure under different conditions where an adversary can try to attack the system. Section B mentions about performance findings of the system. Comparative analysis of the proposed system with the existing encryption schemes is covered in Section C. Going forward, a detailed key size analysis was done in order to determine the appropriate key size to make the system work efficiently and securely. The analysis can be found in Section D.

• A.    Security Findings

The system developed in this paper has proven to be secure under various conditions.

• 1.    Only the mobile user knows his/her location.

• 2.    The adversary cannot have an access to user’s location, as it is sent to the server in an encrypted format.

• 3.    An adversary trying to attack the server cannot gain access to the plain text as he doesn’t have a key. Even then if he tries to attack, since the algorithm applied is probabilistic in nature, every time a new random value is used to encrypt the plain text. Thus, it becomes difficult to crack the cipher text.

• 4.    Even if the adversary has attacked and cracked the plain text, it still doesn’t lead to mobile user’s location as we do not send user’s actual location coordinates but its corresponding index value based on the cell division of the cloaking region.

• 5.    The server does nothing but performs arbitrary calculations on the encrypted data and returns the result to the mobile user. Thus, there is no disclosure of the plain text. There is no key sharing involved. The server has no information about the plain text.

• B.    Complexity Analysis

Analyzing the performance of the algorithms, since the modular multiplication and square computations are cheaper than the exponentiation computations, I have considered the latter over the former. Also, the computations involved in the key generation process can be ignored since it can be precomputed.

Analyzing the three algorithms (Algorithms 1-3), in the kNN query protocol:

Algorithm 1: The mobile app user encrypts the location before sending it to the LBS provider. He computes n encryptions (Paillier encryptions) which means computing about n exponentiations.

Algorithm 2 : The LBS provider computes n2 exponentiations while making calculations on the cipher text.

Algorithm 3 : The mobile app user decrypts the calculated cipher obtained from the server. It involves 1 Paillier decryption i.e. about 2 exponentiation computations.

Table 1. Complexity Analysis

	Operations		No. of exponentiatio ns	Complexi ty
CLIEN T	Mobile App User	n Paillier encryptions	n exp	O(n)
	Mobile App User	1 Paillier decryption	2 exp
SERVE R	LBS Provid er	Exponentiati on calculations	n 2 exp	O( n2)

Table above concludes the complexities involved in algorithm 1-3.

The total computation complexity of the client, mobile app user, is O (n) exp.

The total computation complexity of the server, LBS Provider, is O (n2) exp.

The total communication is 2n log 2 N bits.

• C.    Comparative Analysis

Homomorphism - a better choice for cloud computing.

During my research work I have tried to analyse various encryption schemes applicable on cloud. The following table sums up the analysis based on a few primary characteristics:

Table 2. Comparative Analysis

	Unpadded RSA	ELGAMAL	Goldwasser-Micali	Paillier	Gentry
Usage Platform	Cloud Computing	Cloud Computing	Cloud Computing	Cloud Computing	Cloud Computing
Type of Homomorphic encryption	Multiplicative	Multiplicative	XOR/ Additive -encrypts a single bit at a time.	Additive	Fully
Efficiency and Security	Deterministic and can be cracked using chosen plain text attack	Probabilistic but not secure under chosen cipher text attack.	Not an efficient cryptosystem, as cipher texts may be several hundred times larger than the initial plaintext.	Probabilistic, efficient and simple. It involves only one multiplication for each homomorphic addition and one exponentiation for each homomorphic multiplication.	Efficient as it computes arbitrary number of operations on encrypted data. However practically not possible.

• D.    Key Size Analysis

Analyzing the entire system developed based on varied key sizes lead to a deduction that a key size of 32 bits is appropriate to make the system work and process the queries efficiently. Neither the cipher text is too small nor is the encrypted result from the server too large. This is summarized in Table 3.

Although, the system started working correctly and gave correct encrypted and decrypted results with a key size of 18 bits. It could hence be conclude that for the proposed system to work correctly, minimum key size should be 18 bits. But, taking into consideration other parameters- the cipher text size, the encrypted result size, security parameter, T,- a key size of 32 fits in the best because exceeding that the size of the cipher text in comparison to the plain text becomes exceedingly large.

It was also observed during one of the executions of the system that with increasing key size, the length of the cipher text also increased. For instance, with a key size of 10 the length of the cipher text came out to be 18 bits long, with a key size of 12 the length of the cipher text came out to be 22 bits long, with a key size of 16 the length of the cipher text came out to be 31 bits long and with a key size of 32 the length of the cipher text came out to be 57 bits long.

According to Encryption Performance Improvements of the Paillier Cryptosystem [17], this encryption scheme proves to be efficient if the plain text size is small in comparison to the length of the key, which is the case in our system. However, since the security factor of Paillier cryptosystem is based on hardness of integer factorization, size of modulus n should be large. Therefore choosing a correctly sized value of n is important.

Also, we need to be careful while choosing the value of parameter g . According to [18], equation (4), the value of g should satisfy the condition:

gcd( L ( g^x mod n² ), n )=1

Also, according to the same reference [18],Paillier, value of g should ideally be small for high performance of the algorithm. In my system I have randomly generated the value of g in range 0-9 .

In order to make the system more secure and robust, I have also tried a combination of a key size of 512 bits coupled with a random generator value, g , ranging between 0-9 and a security parameter ,r , atleast 70 bits long for small sized plain text. This combination gave accurate results without much delay. However increasing the key size or value of g or the security parameter here from brought significant time delay in response generation.

Table 3. Key size Analysis (when size(key)=size(g))

Key Size(bi ts)	p	q	Plainte xt size(bit s)	Secuir ty Param eter (bits)	Encryp ted Result from server (bits)	Correct Decryp tion (X/√)
10	5	5	0-3	70	60-80	X
12	6	6	0-3	70	70-100	X
16	8	8	0-3	70	110120	X
18	9	9	0-3	70	130150	√
20	10	10	0-3	70	140150	√
32	16	16	0-3	70	240260	√
64	32	32	0-3	70	500520	√

• VIII.    Conclusion

This paper provides its readers with an idea and mechanism involved in preserving the user’s location using homomorphic encryption scheme.

The scenario that homomorphic encryption supports says that a user can encrypt his data with the public key and transfer the data to cloud. The cloud server then performs computations and calculations on the cipher text. However, because the cloud server doesn’t have the private key, it cannot decrypt the result of the computation.

After the computations have been carried out, the server sends the resultant cipher text back to the server who can at last decrypt the cipher text to get the desired answer.

The same thing happens when we try to ensure location privacy using homomorphic encryption. While sending a location based query to the server, the client hides it and never reveals. Hence the idea of preserving the user’s location is restored.

Using homomorphic encryption to secure data prevents plain text from being exposed[20]. Thus, homomorphic encryption has given a new dimension to cloud storage and security. There are various homomorphic cryptosystems available and now there is a need to develop Fully Homomorphic cryptosystems[20] which meet all the criteria of being compact, correct and applicable on all functions/circuits. With the advent of Fully Homomorphic Cryptosystem, the data has become semantically secure.

Acknowledgement

I would like to convey and extend my sincere thankfulness and gratitude to Dr. Latika Singh and Ms. Mehak Khurana for their kind co-operation, guidance and encouragement which helped me accomplish this project.

I am also highly indebted to Dr. Meena Kumari for her supervision and guidance during the initial stage of the project which kept me motivated towards achieving an accomplished result out of these efforts.

My thanks and appreciations also go to my colleagues and fellow associates in helping me develop the project base .