Логическая модель деградации микропроцессора под воздействием излучения

Существует множество подходов к тому, как выполнить моделирование вычислительной системы [5], которая оказалась под воздействием ионизирующего излучения. При этом работ, которые бы отвечали на вопрос, каким образом можно оценить степень деградации микропроцессора вычислительной системы и сохраняющихся архитектурных возможностей вычислительной системы, не проводилось.

Микропроцессор (а тем более микроконтроллер) не интересен сам по себе, если он не выполняет необходимый функционал с точки зрения вычислительной системы, поэтому рассмотрение процесса его деградации крайне интересно. Однако модели, которая бы отвечала особенностям деградации кристалла применительно к доступным приложениям, в настоящее время не наблюдается.

Целью статьи является построение логической модели деградации кристалла и анализ возможностей ее использования с учетом физических характеристик микропроцессора и поддержки приложений.

Методология

Важно отметить, что при классическом способе анализа влияние состояния на микропроцессор или микросхему рассматривается исключительно с физической точки зрения. Для этого различными авторами используются различные критерии; один из самых популярных – критерий NIEL (Non Ionizing Energy Loss) – неионизационные потери энер-

Логическая модель деградации микропроцессора под воздействием излучения

Приходько Дмитрий Игоревич инженер вычислительных и электронно-вычислительных машин. Научно-исследовательский институт системных исследований Российской академии наук, Москва. Сфера научных интересов: информационные системы; вычислительные системы; операционные системы; эксплуатация вычислительных систем.

гии, под которыми подразумевается часть энергии, расходуемая на повреждение решетки [4]. В одном из последних исследований на момент публикации настоящей статьи показан первичный вариант анализа влияния состояния на микропроцессор или микросхему: «Необходимо знать свойства нескольких транзисторов и NIEL, и этого будет достаточно для прогноза поведения микросхемы».

Тем не менее для оценки микропроцессора такая методика имеет следующие проблемы.

• 1.    Как правило, данные по элементам не отражены в технической документации к микропроцессору, что лишает возможности использовать NIEL.

• 2.    Так как в современных микропроцессорах число транзисторов очень велико (несколько миллиардов), и этот элемент является единственным достоверным элементом, характеризующим микропроцессор, оценивать поведение микропроцессора по нескольким элементам крайне затруднительно.

• 3.    Поскольку микропроцессор в отличие от микросхемы облает более существенным функционалом, исследователей интересует, как будут меняться возможности микропроцессора с точки зрения поддежки приложений, и в каких случаях можно считать микропроцессор непригодным для использования.

Таким образом, с точки зрения исследования деградации микропроцессора [6] наиболее интересной является ситуация, когда микропроцессор в пределах допустимой точности и на некотором временном интервале еще способен исполнять свои функции.

Результаты

Как уже было сказано выше, полагаться на физическую структуру вычислительной системы [6], которая в упрощенном варианте представляет собой микропроцессор, нет возможности из-за отсутствия конкретных параметров в качестве NIEL и невозможности оценить поведение кристалла на уровне элементов.

Рассмотрим следующее особенности микропроцессора.

• 1.    В упрощенном виде микропроцессор можно представить в формате суммы всех транзисторов, так как число транзисторов описано в документации к микропроцессору. Однако это среднее число по документации, и оно не всегда означает, что в этом микро-поцессоре транзисторов ровно столько, сколько указано в документации.

• 2.    В упрощенном виде при простейшем анализе допустимо пренебречь функциональным назначением каждого транзистора в микропроцессоре, потому что если учитывать данный фактор, нужно будет вводить коэффициент стоимости повреждения, для построения которого нужна детальная структура микропроцессора, для постое-ния которой, в свою очередь, нужна схема анализа поведения микропроцессора, но она не всегда доступна.

В микропроцессоре содержатся не только транзисторы, но и диоды, конденсаторы и др., тем не менее число транзисторов и размерные характеристики оборудования, на котором изготовлены транзисторы, приведены в документации. Носителями логической модели микропроцессора являются транзисторы. Для другого типа элементной базы, например, для ламповой микроэлектроники, такими носителями являются триоды, для квантовой элементной базы – оптические транзисторы.

Таким образом, процесс поражения микропроцессоров можно представить как сокращение численности транзисторов в рамках воздействия неблагоприятных факторов окружающей среды. При этом с физической точки зрения процесс характеризуется следующими особенностями:

• •    количество транзисторов всегда конечно;

• •    количество работающих транзисторов при поражении ионизирующим излучением всегда убывает;

• •    полезная площадь кристалла, которая осуществляет вычисления, уменьшается.

Процесс в упрощенном виде можно представить в виде некоторой пандемии, где в качестве «заболевающего» элемента представлен транзистор. Однако в отличие от поведения носителя при обычной пандемии поведение транзистора в микропроцессоре выглядит следующим образом:

• •    транзистор может быть «инфицирован» - есть повреждение, но пока еще не критическое, например, попал нейтрон, тогда атом Si переходит в Si, но с измененными характеристиками (изменился изотоп Si);

• •    транзистор может быть «неинфицирован» - можно использовать;

• •    транзистор «умер» - непригоден для использования;

• •    транзистор может «выздороветь», то есть свойства проводимости у него могут быть восстановлены; это происходит за счет того, что радиация перешла на место контакта, но сам кристалл не «выздоравливает»;

• •    транзисторы являются «бесплодными носителями» пандемии, так как их число никогда не увеличивается в рамках произведенного кристалла;

• •    транзисторы не являются «переносчиками» радиации - они не переносят излучение, так как не перемещаются.

Математический аппарат

Этот факт можно получить через формулу «хищник» – «жертва», которая описывает заимодействие двух видов [7]:

dx       Bxy 2

— = Ax---— Ex dt       1+px dy=-cy - DyL - My y dt 1 + px

Но у нас нет популяции «хищника», поэтому моделирование по модели Базыкина можно описать так:

c =c

- d ( f(x )).

итоговое ^изначаьное

Поскольку изначальное число является константой, то для получения функции скорости роста численности производится дифференцирование по x [7]:

x'

df(x)

- d^T'

Логическая модель деградации микропроцессора под воздействием излучения где d - амплитуда; —— - скорость поражения транзисторов в микропроцессоре. dx

Таким образом, логическая модель сводится полностью к описанному ранее процес су – скорость деградации микропроцессора полностью зависит от скорости деградации транзистора.

Главное отличие логической модели от физической заключается не в том, сколько останется транзисторов а в том, сколько транзисторов достаточно для того, чтобы можно было организовать работу микропроцессора выбранной модели в необходимых режимах [3].

Параметры модели выглядит таким образом.

Верхней планкой процесса деградации кристалла является исходное количество транзисторов.

Нижней планкой процесса является минимальная величина транзисторов, которая обеспечивает нужную работоспособность микропроцессора в необходимом режиме работы.

Функция «гибели» транзистора определяет смену состояний транзистора с целого до того, когда он перестает функционировать. Определяются в зависимости от условий эксперимента.

Рассматривать микропроцессор, когда он не способен выполнять необходимые вычислительные функции с точки зрения логической модели имеет смысл только тогда, когда идет детализация физической структуры микропроцессора и процесс анализа поражения.

Важно отметить, что в некоторых случаях модель может иметь гибридный график, то есть когда идет рассмотрение процесса в нескольких разрядностях, то есть идет анализ по нескольким функциям деградации. Под гибридной моделью следует понимать, что данная модель может иметь различный характер зависимости деградации кристалла от количества транзисторов и коррелирует со сменой режима работы микропроцессора. Например, при применении сильного для транзисторов излучения и сектора повреждения была взята экспонентная функция деградации кристалла, результат которой показан на Рисунке 1.

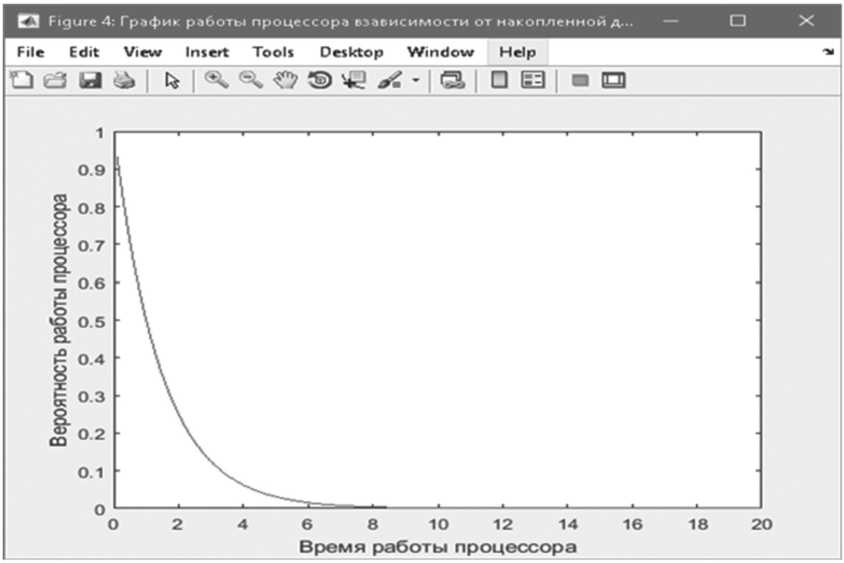
Рисунок 1. Пример использования модели для технического анализа системы

Но это очень упрощенный пример графика для современных вычислительных систем. На реальных графиках модель может дать совершенно другой результат. Например, формула предельной дозы излучения сверхвысокими частотами (далее – СВЧ), полученной транзистором, имеет вид, как на Рисунке 2.

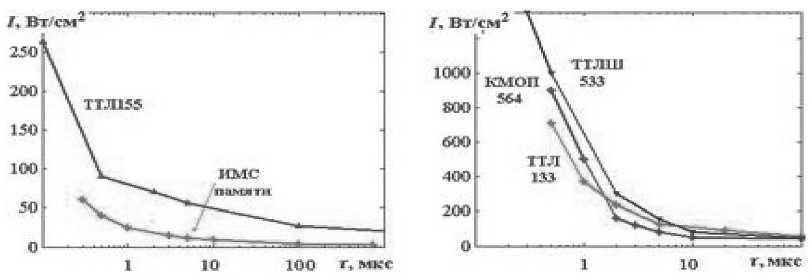
Рисунок 2. График повреждений транзистора и интегральные микросхемы (далее – ИМС) памяти СВЧ-излучением

Видно, что была взята другая зависимость излучения – более детализированная.

Однако ничто не мешает использовать простой параметр – упрощенный коэффициент проводимости как компонент деградации кристалла [3]. Под этим коэффициентом будем понимать следующее:

K = ÑÓÌÌ (t_norm/t_real*exp^(S_Norm*(N_IZL_Norm/N_IZL_REAL)).

Здесь K – коэффициент проводимости транзистора;

N_IZL_Norm – нормальный уровень излучения (уровень излучения, на которое рассчитан транзистор);

N_IZL_REAL – реальный уровень излучения. (уровень, который реально падает на транзистор в текущий момент времени);

t_norm – нормализованное время для уровня воздействия;

t_real – реальное время воздействия излучения реального излучения.

Данный коэффициент вполне пригоден для выполнения оценки. Однако этот параметр при проектировании является крайне упрощенным, так как он не учитывает внутренности транзистора микропроцессора.

Как уже было показано выше, есть коэффициент воздействия на «условный» транзистор. В различных моделях микропроцессора число транзисторов всегда указывается в документации, поэтому можно ограничиться простой и понятной формулой

K_CPY = N_TR*K_TR;

где N_TR – число транзистор;

K_TR – коэффициент транзистор.

Тогда поврежденный сектор можно определить как

Vsec = V*TR_itg/TR_ALL, где V – объем микропроцессора;

TR_itg – количество транзисторов (общее число целых транзисторов);

TR_ALL – реальное количество транзисторов в процессоре, которое берется из документации.

Логическая модель деградации микропроцессора под воздействием излучения

В зависимости от построения этой функции деградации кристалла может быть определена по-разному, и продолжительность работы микропроцессора также будет различной. Более того, можно определить мультиразрядность вычислений.

Таким образом, при правильном анализе и выборе функции отмирания транзистора можно добиться хороших аналитических результатов по работе вычислительной системы и получить представление о том, насколько долго вычислительная система сможет выполнять поставленные перед ней функциональные задачи.

Обсуждение

В отличие от рассматриваемых моделей в работах других исследователей, например, [4; 3], логическая модель обладает серьезным преимуществом – нет необходимости учитывать полную детализацию кристалла , которую в данном случае обеспечивают 2 фактора: граничные условия работы, которые можно определить через функцию перехода, при этом простейшая функция перехода – это коэффициент по числу носителей, и фактор выполнения приложений, что физическая модель в общем случае дать не может – не хватает критериев для оценки потерь.

Заключение

Таким образом, логическая модель выполняет все необходимые для нее требования, позволяя не только описать физический процесс, за который отвечает функция деградации кристалла, которая получена из данных по анализу биологических систем, но и установить стадиальность переходов с точки зрения поддержки приложений.

В перспективе с помощью этой модели можно добиться мультиразрядности вычислительной системы – способности микропроцессора работать на разных уровнях без использования перезагрузки, а также вычислить нужные граничные условия с необходимой точностью, чем не обладает подход физического анализа вычислительной системы.