Логика устойчивости. Деформации симметрий

Рассмотрены виды и типы деформаций симметрий.

Выяснены основные коллизии, необходимые для динамической устойчивости простых дипольных векторных симметрий устойчивости.

Содержание

• 1.    Вступление

• 2.    Деформации симметрий

• 3.    Основные коллизии, необходимые для динамической устойчивости простых дипольных векторных симметрий устойчивости.

• 4.    Выводы

2.    Деформации симметрий

Литература.

1.    Вступление

Векторная симметрия устойчивости является частью Логики устойчивости и участвует в стабилизации многих явлений Природы. Но дипольные векторные симметрии имеют достаточную устойчивость только в определённых условиях.

Абсолютной, (идеальной, совершенной) симметрией устойчивости является такая симметрия, в которой все вектора находятся в совершенно равных условиях, и если их обрезать сферой радиусом “r”, и установить на них шары, то, образованные между ними треугольники, все будут равносторонние, и к каждому шару будут примыкать три треугольника. Такой симметрией устойчивости является только симметрия S = 4 равная начальной геометрической коллизии пространства К= 4. Как видно из [1] и [2], все остальные симметрии являются деформированными.

Деформации симметрий бывают двух видов:

• 1)    номинальные деформации, то есть деформации, вытекающие с числа “m”,

• 2)    реальные (физические) деформации, вызванные каким-то посторонним физическим фактором и искажающим симметрию.

Искажение симметрии может быть несимметричным, такая симметрия называется искажённой (деформированной); или симметричным, тогда симметрия будет неполной и называется пятнистой. В пятнистой симметрии какая-то симметричная часть шаров, изъята из симметрии, при этом оставшаяся часть шаров, должна образовать неполную симметрию, состоящую из симметричных пятен шаров и симметричных пятен пустых посадочных мест. Все искажения симметрий, вызванные числом “m”, являются симметричными, пятнистыми и не приводят к существенному уменьшению их устойчивости, поэтому, невзирая на некоторые отклонения от идеальной симметрии, симметрии для любого числа “m”, если нет дополнительных деформаций, а только искажения от числа “m”, называются номинальными симметриями. Если есть дополнительные деформации, кроме искажений от числа “m”, такие симметрии называются деформированными.

К пятнистым симметриям относятся также комбинированные симметрии, в которых часть трёхточечных посадочных мест по 2 штуки объединены в четырёхточечные посадочные места одним шаром, а фигуры трёхточечных и четырёхточечные мест симметрированые между собой. На рисунке 1 показана пятнистая комбинированная симметрия S12 – S14. В ней имеется простая дипольная симметрия S12 (оранжевые шары 12 шт.). Следующий слой для неё должен быть слой 20, вместо него стоит комбинированная симметрия S14 (серые шары 14 шт.). Они занумерованы. При этом шары 1, 2, 3 и 4 (за рисунком), а также шары 11, 12, 13 и 14 всего 8 шт. стоят по трёхточечным посадочным местам слоя 20. А вместо двух змеек 12 шт. шаров по экватору симметрии, стоит одна змейка из 6 шт. шаров 5, 8, 6, 9, 7 и 10 (за рисунком) по четырёхточечным посадочным местам. Это возможно, потому что экваториальные трёхточечные посадочные места симметрии расположены по 2щт. очень близко друг к другу, и совместно образуют четырёхточечные посадочные места

Для шаров одинакового размера такая симметрия может быть даже более устойчивой, чем номинальная, особенно в тех случаях, когда шары допускают некоторую деформацию.

Посадочные места четырёх, пяти и шести точечных симметрий все состоят из нескольких не равносторонних треугольников [3]. Поэтому на них невозможно установить несколько шаров вместо одного, предусмотренного симметрией, так как они упрутся один в другой. Кроме того, взаимное расположение этих шаров будет не определено, и их вектора не согласуются с общей симметрией системы. Но в динамическом режиме, система с определённым уровнем свободы, имеет возможность деформировать свои составные части, в том числе и симметрии, если они присутствовали в системе. Многоточечные симметрии при определённом направлении деформаций, могут преобразовывать свои многоугольники в равносторонние треугольники, тем самым содействовать преобразованию неустойчивой системы в устойчивую.

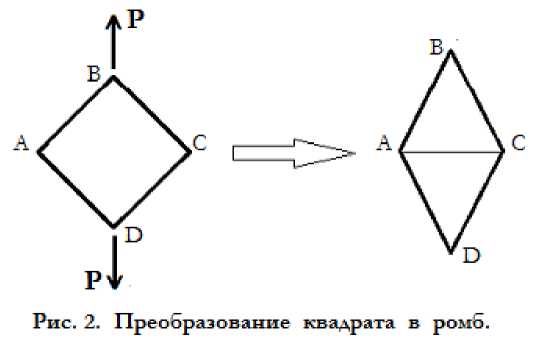
Так квадрат ABCD, если его растянуть по двум противоположным вершинам, усилиями P+P , легко преобразуется в ромб, состоящий из двух равносторонних треугольников (рис. 2). При этом, как видно из развёрток симметрий [2] направления растягивающих усилий должны совпадать с направлением оси диполя симметрии.

Шестиугольник ABCDEF, а их основная масса в составе простых симметрий, усилиями P + P , параллельными оси диполя симметрии, может быть, растянут в два равносторонние треугольники BCD , AEF и прямоугольник ABDE

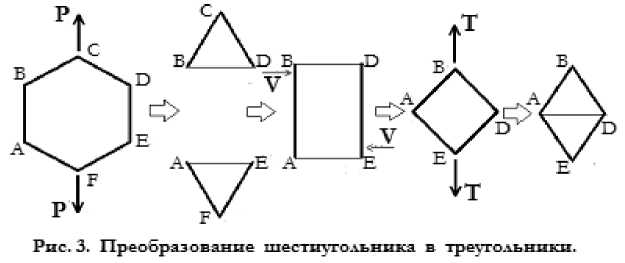
После чего прямоугольник парой сил V + V , может быть развёрнут по оси перпендикулярной оси диполя симметрии и деформирован в квадрат ABDE. Далее квадрат усилиями T + T , параллельными оси диполя, растягивается в ромб, состоящий из треугольников ABD и ADE.

Здесь, как и при преобразовании квадрата, основную роль играют усилия, направленные вдоль оси диполя.

Аналогичным образом может быть преобразован в треугольники и пятиугольник. Возможны и другие преобразования по другой схеме при другом расположении деформирующих сил. В некоторых системах количество составляющих частей может изменяться, кроме того эти составляющие могут переходить из слоя в слой и друг в друга. В этом случае возможности преобразования многоугольников в треугольники увеличивается. Так шестиугольник ABCDEF при переходе в его центр K шара из предыдущего слоя легко превращается в шесть равносторонних треугольников (рис. 4).

с

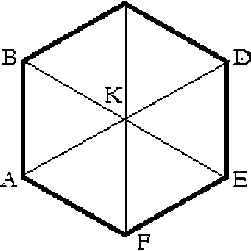
Рис. 4. Шестиугольник с центром.

Кроме того в системах с нежёсткими составляющими, усилия могут быть приложенными не только к вершинам многоугольников, но и к их граням, что ещё больше расширяет возможности преобразования многоугольников в треугольники.

Как показано выше простые дипольные симметрии ещё могут преобразовываться в пятнистые комбинированные симметрии (рис. 1) с достаточно высокой устойчивостью.

3.    Основные коллизии, необходимые для динамической устойчивости простых дипольных векторных симметрий устойчивости

Из- за лёгкости преобразования многоугольников в равносторонние треугольники простые дипольные симметрии могут иметь достаточно высокую устойчивость в динамическом режиме, но она не может быть стабильной и постоянно должна поддерживаться посторонними внешними факторами, при этом эти факторы должны быть не статическими, а динамическими. Самым важным фактором является постоянное растяжение системы вдоль оси симметрии. Именно растяжение, а не сжатие.

Другим не менее важным условием является наличие в системе динамических факторов способных порождать механические усилия по направлениям перпендикулярным оси симметрии, а также под углами к ней. Это необходимо как для преобразования многоугольников в треугольники, так и для смещения их во взаимное расположение, необходимое для симметрии. При этом, так как данная симметрия возможна только в динамическом режиме, то эти перемещения необходимы постоянно, пока существует система, как симметрия устойчивости.

Может возникнуть вопрос, что же будет осуществлять эти оптимальные и довольно сложные перемещения для достижения максимальной устойчивости? Ведь шары, высыпанные на стол, не станут строить какие либо симметрии. Но скользкие шары, помещённые в скользкий мешочек, при его сокращении будут паковаться по самой плотной и самой устойчивой тетраэдрической симметрии. И это, потому что Логика разности учтёт все пространственные производные их взаимных расположений. Аналогично и в динамическом режиме. Но чтобы Логика разности построила устойчивую систему:

• 1)    должна быть теоретическая возможность её построить,

• 2)    вся система должна иметь необходимую степень свободы

• 3)    должны быть какие-то определённые усилия, направленные на хотя бы приближённое выполнение данной задачи, тогда Логика разности построит необходимую систему точно.

4.    Выводы

И наконец, первый внутренний слой симметрии даже теоретически не может построиться по основной трёхточечной симметрии, поэтому никакие преобразования многоугольников в треугольники ему не помогут. Он в сути своей шести точечный на всём протяжении, и только в пред полюсном слое четырёхточечный, а сам полюс, если он выражен шаром, трёхточечный. Как показано в [2], именно потому, что первый слой такой, поэтому и возможна установка на нём второго слоя по основной трёхточечной симметрии устойчивости. Его можно расширить в геометрических размерах, но изменить расположение его составных частей нельзя, иначе с ним не состыкуется второй слой по устойчивой трёхточечной симметрии. Практически изменить его какими - то усилиями, безусловно, возможно, но тогда потеряется устойчивость как таковая. Значит, в данных симметриях их центр всегда будет неустойчив. Поэтому, в системе должны быть какие-то коллизии, которые хотя бы в динамике нивелировали неустойчивость первого слоя симметрии.

• 1)    номинальные деформации, то есть деформации, вытекающие с числа “m”, не нарушают симметрию значительно, поэтому практически не понижают её устойчивость.

• 2)    при помощи определённых деформаций и определённых внешних воздействий, можно получить достаточную устойчивость деформированной векторной дипольной симметрии, если эти деформации и воздействия будут непрерывными в течение всего времени существования симметрии.