Логика устойчивости. Конструкции простых многослойных векторных симметрий устойчивости

Исследованы конструкции простых многослойных векторных симметрий устойчивости, их свойства и особенности.

Оглавление.

• 1.    Вступление

• 2.    Конструкции простых многослойных векторных симметрий.

• 3.    Выводы. Литература

2.    Конструкции простых многослойных векторных симметрий.

1.    Вступление

Совокупность количества и взаимного расположения векторов друг относительно друга называется конструкцией векторной симметрии устойчивости.

Как показано в предыдущем разделе [2], пространственные симметрии устойчивости, могут быть простыми или тетраэдрическими, и простые симметрии получаются дипольными. Следует ещё раз подчеркнуть, что здесь рассматриваются не симметрии, как таковые, а симметрии устойчивости, и на первом плане находится не совершенство симметрии, а её устойчивость, вытекающая из устойчивого расположения её составляющих частей, (векторов или шаров). Для этого каждый вектор или шар симметрии должен находиться в центре равностороннего треугольника, образованного соседними с ним векторами или шарами. Поэтому при исследовании симметрий устойчивости необходимо рассматривать и внутреннюю структуру расположения всех её составляющих частей. В [2] рассматривалось симметрирование двух соседних слоёв симметрии. Здесь же будут рассмотрены многослойные симметрии в полном объёме. В них слоёв более двух, и начинаются они с первого слоя, который опирается сам на себя.

Рассмотрим конструктивные особенности первого семейства симметрий 5 6 8 12 20 36 …, Оно начинается с числа “m” = 5, которое получается симметричным приращением одного направления к симметрии S = 4. Как видно из рис. 1 уже в дробном диапазоне при бесконечно малом приращении, скажем 0,00390625 долей одного целого направления, сразу получается 6 треугольников между началами векторов. При этом симметрия получается не вся выпуклая, а выпуклая с глубокой впадиной. Если бы интерпретация дробных направлений была бы принята как направления, состоящие из штриховых линий, то симметрия была бы вся выпуклая изначально, но треугольников всё равно сразу получилось бы 6 штук. Тогда бы направление EO состояло бы из штрихов, а точка E на нём была бы вне тетраэдра ABCD.

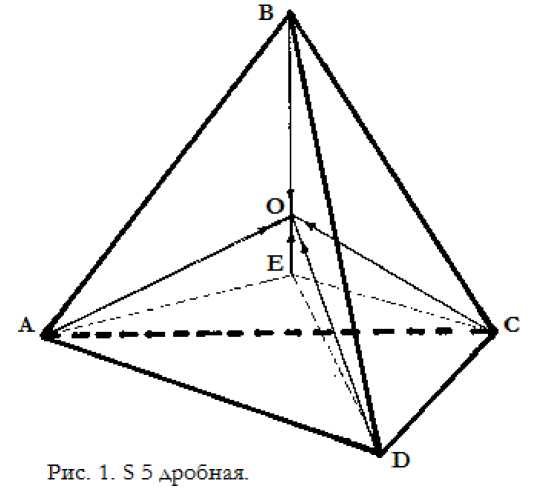
Все рассматриваемые симметрии рассчитываются как симметрии устойчивости по формуле “n = 2m – 4”, поэтому соответствуют Логике устойчивости на всём протяжении, включая дробный диапазон.

Поверху дробной симметрии S 5 можно установить 6 шт. шаров. Три шара на треугольники ABD, ABC и BCD. А три изнутри на треугольники AED, AEC и ECD, они окажутся внутри фигуры AECD, но для симметрии они будут наружными, так как дробная симметрия S 5 имеет центр O и занимает объём, ограниченный началами всех её векторов, то есть фигуру ABCDE (тетраэдр ABCD, у которого есть впадина AECD). Дальше вектор E будет увеличиваться и его начало точка E станет симметрична точке B относительно плоскости ACD, а центр симметрии, точка O окажется в центре равностороннего треугольника ACD. Так получается симметрия устойчивости S 5. Два тетраэдра ABCD и AECD с общей гранью ACD.

Векторы A, C, D находятся в плоскости ACD, расположены под углом 120° один относительно другого, то есть образуют симметрию S 3, а векторы B и E перпендикулярны этой плоскости и отдельно взятые представляют собой симметрию S 2. Таким образом, симметрия S 5 представляет собой сумму двух симметрий. Три шара в симметрии S 3 и два шара в симметрии S 2. Симметрии S 3 и S 2, связаны между собою зависимостью 3 → 2, поэтому, если строить их в два слоя, то необходимо устанавливать три шара в плоскости S 3, а далее на них ставить два шара в симметрии S 2. Если же S 5 строить как однослойную симметрию, тогда все шары нужно располагать в одной сфере, но векторы S 5 необходимо расположить так, как показано выше. При этом вектора пересекутся в одной точке, центре симметрии O, а чтобы шары оказались в одной сфере, их необходимо отодвинуть от центра на такое расстояние, чтобы они физически могли разместиться в этой сфере. При этом шары A, C, D необходимо сместить от центра больше чем шары B и E, так как они сейчас ближе к центру. Таким образом, любая однослойная симметрия, состоящая из шаров, образует внутри себя пустую полость, и в S 4 она минимальная. Кроме того, в S 4 каждый шар симметрии опирается на три остальные шары своей симметрии, что очень важно для величины уровня устойчивости. В тоже время в симметрии S 5, если её строить как один слой симметрии S 5, а не как две симметрии S 3 и S 2, шары B и E опираются на три соседних шара A, C, D, а шары A, C, D опираются на четыре соседних шара. В однослойной симметрии S 5 так же само шары B и E и их вектора будут стоять между тремя шарами A, C, D, а шары A, C, D между четырьмя шарами: B, E и двумя шарами из группы A, C, D. Из-за этого устойчивость S 5 будет существенно ниже, чем S 4. При исследовании коллизий семейств симметрий, шары раздвигать в одну сферу не целесообразно, а следует ставить их поближе друг к другу, так, чтобы они и в первом слое опирались друг на друга. При таком размещении свойства многослойных симметрий, будут выражены ярче и нагляднее, чем в случае размещения каждого слоя в одной сфере.

Симметрия S 5, является минимальной расширяющейся симметрией, имеет такую же геометрическую прогрессию как S 3, но с противоположным знаком, поэтому образование S 5 противоположно образованию S 3, [2]. При этом пространственная симметрия S 4, не вырождается через плоскостную симметрию, а раздваивается: тетраэдры ABCD и AECD, (часть рисунка 2).

Согласно первому семейству симметрию S 5 можно согласовать с симметрией S 6. Действительно, на внешние грани тетраэдров: равносторонние треугольники ABC, BCD, ABD, ACE, CDE и ADE, можно установить 6 штук шаров, и они будут симметричны в пространстве, между собой и симметрированы с симметрией S 5. Будут стоять устойчиво, так как стоят в равносторонних треугольниках. На рис.2 показана конструкция S 5 + S 6.

• A, B, D, E ― шары симметрии S 5. Шар C по центру за рисунком.

• 1,    2, 3, 4, 5, 6 ― шары симметрии S 6.

Так как симметрия S 5 дипольная то и симметричная ей S 6 тоже дипольная. Представляет собой два равносторонних треугольника 1 2 3 и 4 5 6, расположенные в пространстве параллельно друг другу. Согласно первому семейству на S 6 должно установиться 8 штук шаров, но установиться они не смогут, так как им будут мешать шары слоя 5, значит, первое семейство по шарам выродилось. Но для векторов это не существенно, так как шары для наглядности и их можно смещать вдоль линий векторов.

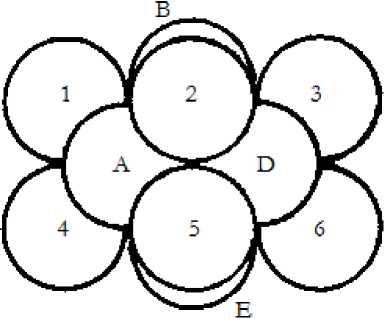
Рис. 2. Симметрия S5 + S6

Существенным является то, что в отличие от нулевого семейства (тетраэдрическая симметрия), которое по векторам никогда не вырождается, это семейство выродилось и по векторам. Действительно, хоть треугольников на поверхности S 6 получилось 8 штук, шесть из них объединились попарно в прямоугольники 1254, 2365 и 1364, а равносторонние треугольники 123 и 456 только по полюсам B и E конструкции.

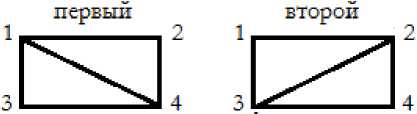
Рис. 3. Варианты разделения четырёхугольника на треугольники.

Прямоугольники не обеспечивают определённости расположения ни шаров, ни векторов, так как имеют два варианта разделения на треугольники, первый или второй. Два вектора в треугольниках 145 и 125 легко переходят в треугольники 142 и 425. Шары в четырёхугольнике упираются друг в друга и легко изменяют своё расположение. Шары слоя 8, расположенные по полюсам будут стоять против полюсных шаров слоя 5, и симметрия здесь выродится по шарам, но не выродится по векторам, так как они внутри треугольников. А 6 боковых шаров выродят симметрию и по шарам и по векторам.

Таким образом, слой 8 на слое 6 стоит неустойчиво, как по шарам, так и по векторам. Если эту многослойную симметрию преобразовать в однослойную S = 5 + 6 + 8 = 19, то в такой конструкции она тоже будет неустойчива.

Чтобы продолжить первое семейство симметрий необходимо отказаться от слоя 5, а слой 6 необходимо построить таким образом, чтобы с ним симметрировался слой 8. Для этого его необходимо строить по Логике устойчивости (n = 2m – 4), начиная с бесконечно малого, но строго определённого для “m = 6”, приращения к симметрии S = 4. В разделе [2] составлены таблицы таких построений для начальных нечётных целых чисел номинальной таблицы семейств симметрий. Аналогичным образом можно составить такие таблицы для чётных чисел.

Число дополнительных направлений для чисел:

6           6 – 4 = 2

8           8 – 4 = 4

10         10 – 4 = 6

12         12 – 4 = 8

и так далее.

Так как вся векторная симметрия устойчивости определена одной закономерностью n = 2m – 4, то перевод чётных чисел “n” = 6, 8, 10, 12… со статуса “n” в статус “m”, начальные числа полной таблицы семейств, достигается простым смещением всего семейства влево до тех пор, пока необходимое число “n” не попадёт в колонку “m”. При этом целые числа, предшествующие выбранному чётному числу, попадают в дробный диапазон и преобразуются в дробную конструкцию.

Значит теперь в таблице дробных симметрий:

перед числом m = 6 число d1 = 5 будет обозначать 4 + 0,5 x 2

8 6 4 + 0,5 x 4 10 7 4 + 0,5 x 6 12 8 4 + 0,5 x 8 и так далее.

Аналогично, [2], чтобы не нарушить устойчивость, число новых формирующихся направлений 2, 4, 6, 8, 10… должно состоять из суммы положительных троек и положительных или отрицательных единиц:

• 2    = +3 – 1

• 4    = +3 + 1

• 6    = +3 + 3

• 8    = +3 +3 +3 – 1

10 = +3 +3 +3 + 1

12 = +3 +3 +3 + 3

и так далее.

Таким образом, чтобы построить симметрию S 6, необходимо до S 4 добавить 2 вектора, то есть вырастить 3 вектора по трём граням тетраэдра и убрать вектор по вершине, расположенной между этими гранями, как показано на рис. 4.

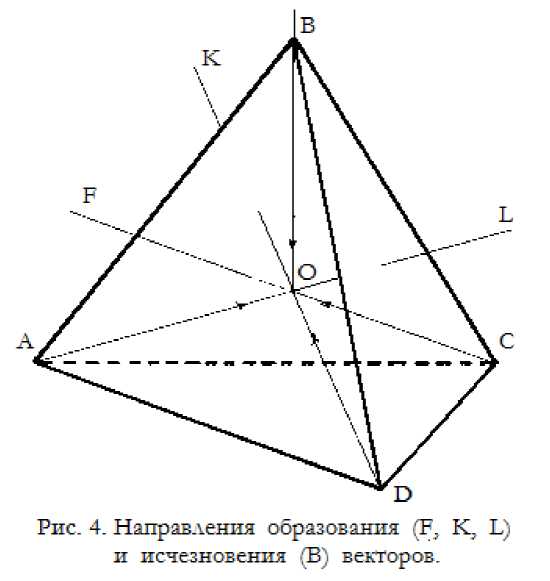
В результате преобразования S 4 в S 6 получается симметрия, состоящая из шести шаров по три штуки в двух параллельных плоскостях FKL и ACD. Шары F, K, L в гранях ABD, ABC, DBC, а шары A, C, D ─ по вершинам A, C, D тетраэдра ABCD. Из свойств тетраэдра вытекает, что первая тройка шаров развёрнута относительно второй на угол 60°, кроме того шары A и L, а также шары D и K и шары C и F находятся попарно на одной линии, проходящей через центр симметрии. Данная симметрия похожая на 159

ту симметрию S 6, что получилась на S 5, но в ней теперь верхняя и нижняя (по рисунку), тройки шаров развёрнуты друг относительно друга на угол 60°. Из-за этого симметрию S 6 можно рассматривать как сумму двух симметрий S 3 согласованных между собой.

Получилась очень красивая симметрия S 6. Если соединить линиями центры противоположных шаров, то линии A L, D K и C F образуют декартовую систему координат с центром в центре симметрии, но эта симметрия неустойчива, так как каждый её шар опирается на четыре соседних шара. Тем не менее, на поверхности этой S 6 образовалось 8 трёхточечных углублений (посадочных мест), куда возможно устойчиво установить 8 шаров. Два по полюсам симметрии (1 и 2), а 6 штук по экватору змейкой, три чуть выше экватора, а три чуть ниже. На рисунке показаны посадочные места 3, 4, 5, а 6, 7, 8 за рисунком, при этом они диаметрально противоположны 3, 4, 5.

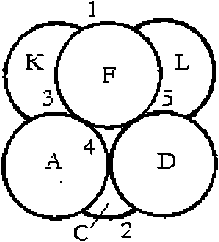
Рис. 5. Симметрия S б

На посадочные места 1, 2, 3, 4, 5, 6, 7, 8 устойчиво установятся шары слоя 8 и расположатся в пространстве точно так, как расположены посадочные места. Поверхность, построенной таким образом и согласованной с S 6, симметрии S 8 представляет собой 6 штук квадратов, расположенных по 3 штуки в районе полюсов симметрии. Один из них 3 1 5 4 с центром F хорошо виден на рисунке, а в состав других входят один, два или три посадочных места из группы 6, 7, 8, расположенных за рисунком. Треугольников, согласно первому семейству симметрий 12 штук, но они объединены в шесть квадратов, три из них объединены одним из углов в верхнем полюсе 1, а три других в нижнем полюсе 2. Квадраты не обеспечивают устойчивости слоя 12 [3]. Из-за этого, чтобы продолжить первое семейство симметрий, необходимо отказаться от слоя 6 и перестроить конструкцию S 8, таким образом, как была построена S 6 из тетраэдрической симметрии S 4.

Для построения S 8 необходимо до S 4 добавить четыре вектора 4 = + 3 + 1 (см. выше). То есть вырастить 4 штуки векторов. Здесь возможна ошибка, так как может создаться впечатление, что можно растить вектора по четырём граням. Это не так. В формуле для простых векторных симметрий добавка 4 = + 3 + 1 представляет собой три новых вектора + 3 по граням, и + 1 это новый вектор по новой вершине. Если в данном случае вырастить четыре вектора по четырём граням, то получится не простая, а тетраэдрическая симметрия с восьми векторов S 4 + S 4, и из двух слоёв, а необходимо строить один слой простой симметрии S 8. Для исследования общих свойств векторных симметрий устойчивости, необходимо при построении S 8 до симметрии S 4 добавлять вектора в конструкции 4 = +3 +1. Только тогда будет получена S 8 в первом семействе симметрий 5 6 8 12 20 36… , и эта симметрия S 8 будет конструктивно отличаться от тетраэдрической S 8. Поэтому, хоть в данном конкретном случае есть возможность строить тетраэдрическую симметрию, всё равно необходимо строить осевую. Здесь рассматриваются простые симметрии, а они все дипольные (осевые). Тетраэдрические симметрии будут рассмотрены отдельно в одном из следующих разделов.

Сравним формулу построения S 8 (4 = +3 +1) с формулой построения S 6 (2 = +3 – 1). Они отличаются тем, что при построении S 6 устраняется один вектор по вершине B тетраэдра, а при построении S 8 наоборот такой вектор необходимо добавлять, и, чтобы образовать новую вершину и не нарушить симметрию, то, если использовались вектора F, K, L, его можно добавлять только по центру грани ACD (см. рис. 4). Исходя из этого, и строится симметрия S 8.

Как и при построении S 6 строятся вектора F, K, L в гранях ABD, ABC и BCD тетраэдра ABCD, (см. рис. 4), но вектор B теперь не убирается, а наоборот добавляется вектор E противоположный вектору B и расположенный по центру грани ACD.

Симметрия S 8 из шаров показана на рис. 6.

Конструкция симметрии S 8 представляет собой два отдельных тетраэдра KFLB и ACDE (вершина C за рисунком), развёрнутых друг относительно друга на угол 60°, с центром на осевой линии между тетраэдрами.

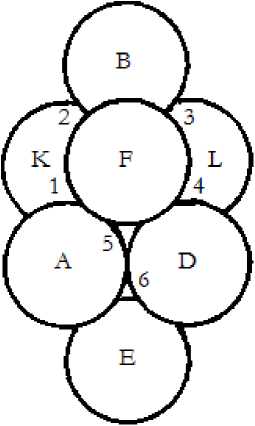
Рис, 6. Симметрия S 8.

Выше утверждалось, что нельзя добавлять 4шт. векторов по граням. А добавили всё же 4шт. векторов по центрам четырёх граней. Это не совсем так. Если бы добавили 4шт. векторов по центрам четырёх граней, то получили бы второй слой круглой тетраэдрической симметрии. А необходимо получить один слой простой симметрии. Для этого вектора F, K, L построили в гранях, а чтобы вершина B оставалась вершиной однослойной S 8, шар B, вершину первичного тетраэдра, сместили вверх (по рисунку). А шар E, установленный в грань ACD, автоматически становится тоже вершиной. С рисунка 6 симметрию S 8 можно представлять как сумму двух симметрий S 8 = S 6 + S 2. При этом нельзя утверждать, что S 8 = S 4 + S 4 , хотя по рисунку оно так и есть. Действительно это две симметрии S 4 , приставленные одна к другой гранями и развёрнутые друг относительно друга на угол 60°. Такая интерпретация, в общем, тоже правильная, но не имеет отношения к рассматриваемым простым симметриям устойчивости, как к таковым. Потому что при такой интерпретации получается два центра, и две отдельные симметрии, а здесь рассматриваются симметрии устойчивости, как конструкции симметричных в пространстве векторов, направленных к единому центру. Поэтому симметрию S 8 необходимо рассматривать только как сумму симметрий S 6 и S 2 с общим центром между тетраэдрами KFLB и

ACDE. При такой интерпретации центры S 6 и S 2 совпадают в пространстве, а при S 8 = S 4 + S 4 центры симметрий S 4 находятся в двух разных точках пространства. Симметрию S 8 = S 4 + S 4 можно построить с единым центром, если по граням первой S 4 установить вершины второй S 4. При этом шар B не поднимается вверх, а остаётся опираться на шары A, C, D. Но это будет два слоя тетраэдрической симметрии. Здесь же рассматривается один слой простой симметрии, и он однозначно равен S 8 = S 6 + S 2.

На рис. 6 видно шесть трёхточечных посадочных мест 1, 2, 3, 4, 5, 6 для шаров следующего слоя. 1, 2, 3, 4, 5 в форме пятиугольника вверху, и одно посадочное место 6 внизу рисунка. Если, изображённую симметрию S 8, поворачивать вокруг оси на угол 60°, то данное изображение симметрии можно увидеть три раза. Если изображение повернуть на угол 30°, то пятиугольник окажется внизу, а посадочное место, вверху. Если дальше поворачивать на угол 60°, то такое изображение можно увидеть тоже три раза. Всего посадочных мест 12 штук.

Изображение симметрии S 8 поворачивалось, чтобы показать особенности её конструкции, при этом одни и те же посадочные места попадали в разные изображения в разных сочетаниях. Чтобы посчитать посадочные места необходимо взять первое изображение, пятиугольник (вверху) и место (внизу), и вид симметрии сзади рисунка, там тоже будет пятиугольник, но внизу, и место, но теперь вверху. На эти посадочные места и установятся шары слоя 12, поэтому слой 12 будет иметь выше описанную конфигурацию.

И в этой конфигурации в двух местах посадочные места слоя 8 образуют пятиугольники. Это не те пятиугольники, которые рассматривались в предыдущем разделе [3] (пятиточечные симметрии). В этих пятиугольниках по их центрах стоят шары предыдущего слоя 8, и они образуют 5 посадочных мест, далёких один от другого, на которые свободно устанавливаются по трёхточечной симметрии 5 шаров следующего слоя 12. Шестой шар устанавливается в посадочное место 6. На обратной стороне рис. 6 аналогично установится ещё 6 шаров. Так получится симметрия S = 12, согласованная по трёх точке с симметрией S = 8. Данных пятиугольников два, если их брать из разных посадочных мест. Но если эту конструкцию поворачивать вокруг центральной оси, как показано выше, то можно найти шесть пятиугольников, состоящих из разных комбинаций посадочных мест. На все посадочные места слоя 8 установятся шары слоя 12. И они опять образуют шесть пятиугольников, но уже без центрального шара предыдущего слоя 12. Теперь это будут пятиугольники, рассмотренные в разделе [3]. И хоть они будут ещё дальше один от другого, на них, чтобы не нарушить логику простой симметрии устойчивости, необходимо устанавливать по 3 шара в каждый, что невозможно из-за потери устойчивости (см. [3]). Таким образом, слой 12 нормально установится на слой 8, но так, что слой 20 на него устойчиво установиться не сможет. Симметрия S = 12 будет выглядеть следующим образом: три шара по трём посадочным местам вокруг полюсного шара “B”, куда войдут посадочные места 2 и 3, а также посадочное место на обратной стороне рисунка, аналогичная тройка шаров слоя 12 образуется вокруг другого полюсного шара “E”, посадочное место 6 и два за рисунком. Остальные 6 шаров слоя 12 расположатся по экватору змейкой. Тогда шары 2, 3 и третий за рисунком, а также шар 6 и два за рисунком, создадут нормальные трёхточечные посадочные места для полюсных шаров слоя 20. А совместно с шарами змейки они создадут шесть пятиугольников. Три вокруг верхнего полюса, а три вокруг нижнего. 3 х 3 +3 х 3 = 18. Так что в слое 20 только 2 шара будут стоять устойчиво, а остальные 20 – 2 = 18 неустойчиво.

Чтобы продолжить первое семейство дальше, необходимо отказаться от симметрии S 8, а симметрию S 12 построить с S 4, добавив к ней 8 штук векторов по схеме 8 = + 3 + 3 + 3 – 1. Для этого, в тетраэдре ABCD (см. рис 4) убираем вектор B и строим вектора F, K, L. Получилась симметрия S 6. Чтобы получить S 12, необходимо добавить ещё две тройки. Их можно добавлять обе сверху или обе снизу, а можно по одной сверху и снизу. Для конструкции симметрии это не имеет значения. Например, в грани ACD посредине между векторами A, C и D строим вектора M, N и P, а ближе к оси симметрии между этими векторами строим ещё три вектора R, V и T, как показано на рис. 7. Последние три вектора можно строить не между векторами M, N и P, а между векторами F, K и L. Но обязательно, чтобы не нарушить симметрию устойчивости, их необходимо строить посредине между вышеуказанными векторами и ближе к оси, чтобы сместить их и их шары вдоль оси симметрии. При таком построении будет обеспечена симметрия, так как все соседние тройки будут развёрнуты друг относительно друга на угол 60°. Построенная таким образом симметрия S 12 показана на рис. 7. В результате получается осевая симметрия S 12, в виде фигуры из четырёх треугольников, размещённых вдоль оси и развёрнутых один относительно другого на угол 60°. На поверхности этой фигуры расположено 20

трёхточечных посадочных мест для размещения шаров или векторов следующего слоя 20. Два из них 1 и 2 расположены по полюсам симметрии, а 18 штук в виде трёх змеек по 6 шаров в каждой. Одна по экватору 6 + 7 + 8 + (три за рисунком), а две по верхней и нижней широте, если для определённости полюса назвать верхним и нижним. Верхняя змейка 3 + 4 + 5 + (три за рисунком), а нижняя 9 + 10 + 11 + (три за рисунком). По всем 20 трёхточечным посадочным местам устойчиво установятся шары слоя 20.

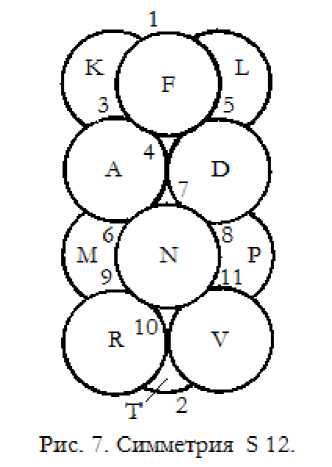
Следует заметить, что на близко расположенные посадочные места 4 и 7, 6 и 9 и другие, шары такого же размера, как в слое 12 установить невозможно. Но для векторной симметрии устойчивости это не принципиально, так как основными составляющими здесь являются вектора, а шары для наглядности, и их можно заменить меньшими. При расчётах конкретных систем размеры составляющих, безусловно, необходимо учитывать. Кроме того эту симметрию из четырёх плоско параллельных троек можно растянуть вдоль оси, и хоть для шаров она потеряет устойчивость, для векторов она будет оставаться симметрией устойчивости, если при этом взаимное расположение шаров не менять.

Конфигурация расположения посадочных мест слоя 20. У полюсов будет по три квадрата, один из них 1 5 4 3 у верхнего полюса хорошо виден на рисунке. Они дадут 2 х 3 х 2 = 12 треугольников для следующего слоя 36. Три змейки создадут шесть шестиугольников, один из них 7 8 11 10 9 6 (см. рис. 7). Это 6 х 4 = 24 треугольника. Всего 12 + 24 = 36, но все они в четырёхточечных и шести точечных посадочных местах, поэтому ни один шар слоя 36 не будет стоять устойчиво.

Чтобы продолжать строить семейство дальше необходимо строить симметрию S 20 с S 4 и на ней строить S 36.

Так как простые осевые симметрии устойчивости строятся аналогично, то для упрощения дальнейших расчётов целесообразно с предыдущего материала учитывать следующие закономерности:

• 1.    Если первая (построенная с S 4) симметрия S 6 не имеет полюсных шаров, тогда следующая за ней S 8 имеет их 2 шт. а остальные шары 6 шт. располагает змейкой вокруг оси. Третья по семейству симметрия S 12 получается неустойчивой, так как змейка, примыкая к полюсному шару, располагает шары слоя 12 в квадратах.

• 2.    Если первая (построенная с S 4) симметрия S 8 имеет полюсные шары, тогда следующая за ней S 12 устанавливает на полюса по три шара, а остальные змейкой по экватору. Третья по семейству симметрия S 20 получится опять неустойчивой, так как змейка, примыкающая к полюсной тройке, располагает посадочные места пятиугольниками.

• 3.    Если первая симметрия S 12 и более, тогда следующие симметрии S 20 и более имеют несколько змеек, которые стыкуясь между собой, образуют шести угольники, из-за чего третьи симметрии S 36 и более, получаются неустойчивы.

• 4.    Начальные осевые симметрии (полученные из S 4) очень вытянуты вдоль оси, а добавление слоёв семейства скругляет их, но при этом нарушается устойчивость уже в третьем слое.

• 5.    Семейство симметрий не может обеспечить устойчивость по всему своему диапазону, а только для двух соседних слоёв. Значит, в теоретических расчётах нельзя брать более двух соседних слоёв. Тем не менее, таблицы семейств симметрий имеют большое прикладное значение, так как показывают какое количество векторов, с каким количеством, может симметрироваться. Более целесообразно пользоваться номинальной таблицей, так как она более компактная, чем полная.

Второе, третье, четвёртое и так далее семейства строятся аналогично первому. Так как N = 4 + Pi , а 4 = +3 + 1 , то можно, учитывая предыдущий опыт, не вычислять дополнительные направления, а строить необходимую симметрию сразу как сумму положительных троек (+3) и плюс одна или две положительных единиц (+1). Так как симметрия это число 4 = +3 + 1 плюс дополнительные формирующиеся направления, то:

• 5    = 4 + 1 = +3 +1 +1

• 6    = 4 + 2 = +3 +1 +2 = +3 + 1 +3 – 1 = +3 +3

• 7    = 4 + 3 = +3 +1 +3 = +3 +3 +1

• 8    = 4 + 4 = +3 +1 +3 + 1 = +3 +3 +1 +1

• 9    = 4 + 5 = +3 +1 +3 +3 – 1 = +3 +3 +3

• 10    = 4 + 6 = +3 +1 +3 +3 = +3 +3 +3 +1

• 11    = 4 + 7 = +3 +1 +3 +3 +1 = +3 +3 +3 +1+1

• 12    = 4 + 8 = +3 +1 +3 +3 +3 – 1 = +3 +3 +3+3

• 13    = 4 + 9 = +3 +1 +3 +3 +3 = +3 +3 +3 +3+1

• 14    = 4 + 10 = +3 +1 +3 +3 +3 +1 = +3 +3 +3 +3 +1+1

• 15    = 4 + 11 = +3 +1 +3 +3 +3 +3 – 1 = +3 +3 +3 +3+3

• 16    = 4 + 12 = +3 +1 +3 +3 +3 +3 = +3 +3 +3 +3 +3+1

• 17    = 4 + 13 = +3 +1 +3 +3 +3 +3 +1 = +3 +3 +3 +3 +3 +1 +1

и так далее.

С полученной таблицы видно, что семейства симметрий m = 5, 9, 11,15, 17 … представляют собой симметричные диполи, и чётные числа этих семейств n = 6, 8, 12, 14 … также симметричные диполи. А семейства m = 7, 13 … несимметричные диполи, и чётные числа этих семейств n = 10, 16 … также несимметричные диполи.

В любом случае, если количество векторов симметрии кратное числу 3 (3i), или кратное числу 3 плюс 2 (3i + 2), тогда диполь симметричен, а если количество векторов кратное числу 3 плюс 1 (3i + 1), тогда диполь несимметричен (здесь i = 1, 2, 3, 4 …). Симметричность или несимметричность диполя выражена только в том, что в симметричных диполях по обоих полюсах есть вектора (шары) или по обоих полюсах их нет, а в несимметричных диполях на одном полюсе есть вектор (шар), а на другом полюсе его нет. А остальное тело симметрии состоит из симметричных относительно оси симметрии троек, развёрнутых друг относительно друга на угол 60°.

Таким образом, простые симметрии крайне похожие между собой, и каждая из них представляет собой сумму меньших по размеру симметрий. Устойчиво симметрируются между собой только два соседних слоя семейства.

Для полноты материала в таблице подана и первая расширяющаяся симметрия S 5 (5 = +3 +1 +1). Для ещё более полной таблицы в ней необходимо подать и S 4 при этом 4 = +3 +1. Она не подана, так как S 4 это тетраэдрическая симметрия, равная начальной (минимальной) коллизии пространства, имеет специфические особенности и не расширяется. Тем не менее, 4 = +3 +1 свидетельствует о том, что она является частным случаем простых пространственных симметрий и не имеет принципиального отличия от них. В этой же таблице можно было бы подать и S 3, где 3 = +3, и S 2, где 2 = +1 +1, а также S 1, где 1 = +1. Они не поданы, так как это участок вырождения пространственных симметрий, и более целесообразно их рассматривать отдельной таблицей:

• 1    = +1

• 2    = +1 +1

• 3    = +3

• 4    = +3 +1.

3. Выводы

С этих двух таблиц вытекает, что все без исключения симметрии устойчивости имеют одну и ту же природу.

Хотя для чисел 0 и 1 нет симметрий вообще, 2 это осевая (линейная), 3 — плоскостная симметрия, но если для полноты материала их тоже рассматривать, то для всех чисел (количества векторов) m = 0, 1, 2, 3, 4, 5, 6, 7… симметрии будут получаться с суммы предыдущих симметрий, состоящих только из троек (для вырождающихся симметрий из ничего), путём добавления добавки. Добавка в такой закономерности: +1, +1+1, +3, +1, +1+1, +3, +1, +1+1, +3, +1…

0    1    2    3     4    5    6    7     8    9    10

0 +1 +1+1 +3 +1 +1+1 +3 +1 +1+1 +3   +1.

Чтобы определить из этой таблицы конструктивную формулу любой симметрии, например S 10, необходимо сложить все предыдущие тройки (для чисел 3, 6, 9), и добавить добавку для числа 10, то есть: +3 +3 +3 +1.

Ещё можно, учитывая кратность симметрий, (см. выше), количество векторов симметрии разделить на 3 и записать полученное число в виде положительных троек. Если получился остаток, то добавить его в виде одной или двух положительных единиц.

Первый слой симметрий это самый внутренний слой, который опирается сам на себя. В простых симметриях только в S 4 все шары опираются на три шара своего слоя. В сужающихся семействах S 3 все шары симметрии опираются на два шара своего слоя, а в S 2 на один. Во всех расширяющихся семействах полюсные шары, если 168

они есть, опираются на три шара своего слоя. Шары, расположенные рядом с полюсом на четыре, если полюсного шара нет, или на пять, если полюсный шар есть. Все остальные ближе к экватору симметрии на шесть.

Таким образом, внутренний слой простой векторной симметрии в первом слое неустойчив. Устойчивым является только стык его со следующим слоем. При этом на полюсах его устойчивость выше, а по мере приближения к экватору понижается.

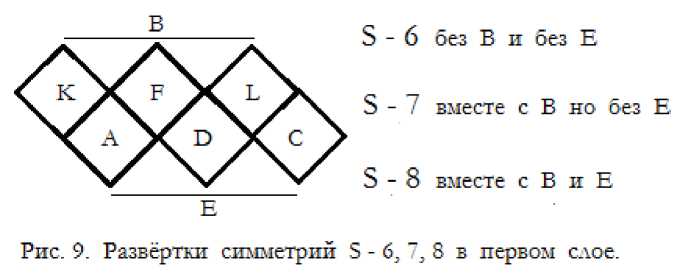
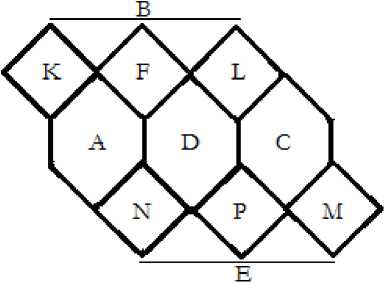
Ниже на рисунках 8, 9, 10, 11 показаны развёртки первых слоёв простых векторных симметрий устойчивости S = 5 ÷ 14.

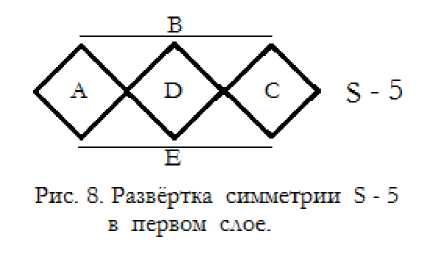
Все шары второго слоя симметрий опираются на три шара первого слоя, и всегда стоят устойчиво. На развёртках они находятся в точках стыка трёх фигур, показанных на рисунках.

Третий слой симметрии, как показано выше, всегда стоит неустойчиво, потому что треугольники его посадочных мест объединяются в квадраты, пятиугольники или шестиугольники.

Таким образом, по основной трёхточечной симметрии устойчивости стыкуются только два соседних слоя.

S - 9 без В и без Е

• S-    10 вместе с В но без Е

• S-    и вместе с В и Е

Рис. 10. Развёртки симметрий 5-9,10,11 в первом слое.

В номинальной таблице семейств трёхточечных симметрий для любого номинального числа, предшествующее ему называется нижним симметричным числом, а последующее верхним. По трёхточечной симметрии можно симетрировать только нижнее с номинальным или номинальное с верхним, и невозможно симетрировать все три одновременно. Это правило справедливо для любой пары чисел в любом семействе.

Шары первого слоя можно отдалить от центральной линии и расположить их в сфере, но для устойчивой стыковки его со вторым слоем системы, взаимное их расположение должно быть таким, каким оно получено в данном исследовании. При этом устойчивость симметрии не увеличится. Если шары первого слоя опирались на четыре, пять или шесть шаров своего слоя, то теперь они окажутся между четырьмя, пятью или шестью соседними шарами. Таким же окажется и расположение их векторов, и первый слой симметрии всё равно будет неустойчив.

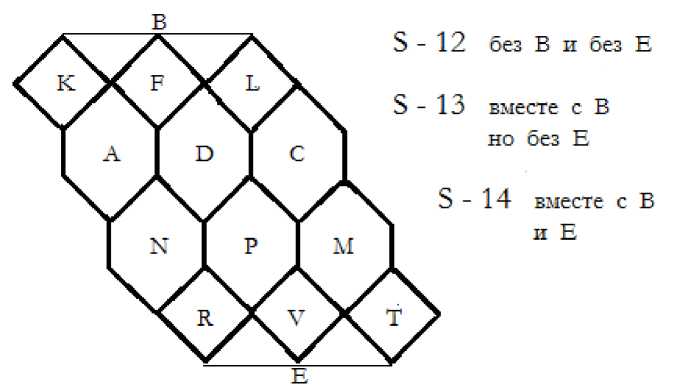
Рис, 11. Развёртки симметрий S - 12, 13, 14 в первом слое.

Таким образом, исследование векторных симметрий устойчивости начиналось как исследование круглых сфер образных симметрий с единым центром, а закончилось тем, что они дипольные и сильно растянутые вдоль какой-то одной оси. При этом с ростом количества векторов они всё больше и больше растягиваются вдоль оси симметрии.

Противоречий между первым разделом теории [2] и данным разделом нет. В первом разделе рассматривались условия устойчивости только между двумя соседними слоями круглой шарообразной симметрии. Вопрос о геометрической форме и конструкции всего семейства симметрий не рассматривался, Сейчас же семейство симметрий рассматривалось как целое с учётом всех его слоёв, в том числе и первого самого внутреннего слоя. Оказалось что формулы, полученные в [2], справедливы для простых симметрий с любым числом векторов, но форма их с ростом числа векторов с круглой превращается в дипольную. Согласоваться может только два соседних слоя, при этом первый слой трёхточечный только в S 4, в остальных симметриях первый слой четырёх, пяти или шести точечный и неустойчив. Значит, устойчивой простая симметрия может быть только в виде тонкой длинной трубки.

Как будет показано в следующем разделе «Топология вихревого движения», в динамических системах с определённым уровнем степеней свободы возможна стабилизация и повышение устойчивости простых симметрий за счёт определённых дополнительных условий.

Строить же статические устойчивые многослойные симметрии по простым расширяющимся семействам невозможно, из-за чего статические устойчивые объекты, атомы, строятся по тетраэдрическим симметриям с устойчивым центром. Эти симметрии подробно будут рассмотрены в одном из следующих разделов теории. Но данное исследование необходимо и для расчёта тетраэдрических симметрий, так как они, как показано выше, являются частным случаем простых симметрий, и, невзирая на значительное внешнее отличие, имеют много общих закономерностей.