Логистический подход к моделированию фракционирования сыпучих материалов

Разделение на фракции является необходимым технологическим звеном в процессе подготовки разнообразных сыпучих и гранулированных материалов к их дальнейшему использованию. В данной работе рассматривается сыпучий материал, частицы которого различны по крупности, а плотность вещества всех частиц примерно одинакова. В качестве такого материала рассматривается щепа.

Размеры и форма частиц технологической щепы должны отвечать определенным требованиям [1], [2]. Поэтому необходимо разделение массива частиц на фракции. Для фракционирования сыпучих материалов выпускается оборудование с достаточно широким спектром технологических характеристик. Например, указанные на сайте http://www.pbm.onego.ru/ промышленные установки способны перерабатывать от 80 до 950 насыпных кубических метров щепы в час, обеспечивая эффективность извлечения фракций до 85 %.

В современных экономических условиях конкурентоспособность оборудования достигается при

выполнении ряда условий, к которым относятся: снижение материалоемкости и энергопотребления; повышение надежности и уменьшение эксплуатационных затрат; достаточная универсальность и технологическая гибкость, то есть возможность эффективного функционирования в определенном диапазоне технологических параметров.

В данной работе рассматриваются вопросы, связанные с обоснованием рекомендаций по совершенствованию конструктивно-технологических параметров фракционирования щепы методом рассева на основе применения результатов математического моделирования данного технологического процесса.

Рассматриваемая далее задача построения математической модели относится к классу задач моделирования технологических процессов разделения на фракции сыпучих и гранулированных материалов. При этом с учетом особенностей оборудования и свойств сыпучего материала выполняется разбиение данного класса на подклассы задач, появляющихся при моделировании процессов разделения на фракции разновидностей сыпучих материалов, например песка и щебня в строительной отрасли, щепы и древесных топливных гранул (пеллет) в целлюлознобумажной и топливной промышленности, руды на горно-обогатительных предприятиях и т. д.

Большие объемы сыпучих материалов, подлежащих разделению на фракции, возрастающие требования к качеству выпускаемой продукции, к материалоемкости, надежности, универсальности и энергопотреблению оборудования, к экономии затрат на его эксплуатацию предопределяют актуальность исследований, выполняемых с целью совершенствования конструктивнотехнологических параметров установок для фракционирования. Для достижения указанной цели необходимо решение комплекса многоплановых задач с применением методов математического моделирования. Необходимы также технологические эксперименты в целях проверки адекватности математических моделей.

Современное состояние экспериментальных и теоретических исследований в области моделирования фракционирования сыпучих строительных материалов отражено, например, в работе [9]. Заметим, что некоторые типы современного оборудования, отвечающие требованиям технологической гибкости, одинаково пригодны для фракционирования минеральных и органических сыпучих материалов [7]. По этой причине результаты решения задач одного из указанных выше подклассов в определенной мере представляют интерес и при рассмотрении других задач данного класса. Например, для разработки методики решения технологической задачи о фракционировании щепы представляют интерес результаты работ [5], [9], [11].

Некоторые особенности фракционирования щепы методом рассева рассмотрены в статье [6], в которой приведена также библиография по затронутой теме. Дополняя эти данные, отметим, что проблема фракционирования сыпучих материалов привлекает внимание исследователей на протяжении всей истории развития промышленного производства. К числу первых работ в области теории фракционирования относится исследование Н. Е. Жуковского [4], выполненное в 1896 году. В этой работе предложена теория движения просеваемого (надрешетного) продукта по поверхности плоского сита, а также обосновано новое для своего времени конструктивное решение устройства для рассева сыпучего материала.

В современной технической литературе фракционирование сыпучего материала методом рассева часто обозначают термином «грохочение» [7], [9].

Анализ литературы показал, что до настоящего времени модели процесса фракционирования не позволяют ответить на многие вопросы, возникающие при проектировании и эксплуатации соответствующего оборудования, что отмечается также в работе [9], в которой с применением теории цепей Маркова предложена математическая модель фракционирования сыпучих материалов на вибрационных грохотах периодического и непрерывного действия.

Рассмотрим иной подход к построению модели фракционирования сыпучего материала. Следуя общепринятой методологии математического моделирования, рассмотрим прежде всего данный технологический процесс с физической точки зрения. Затем составим математическое описание физической модели и воспользуемся полученной в итоге математической моделью для анализа закономерностей процесса рассева.

ФИЗИЧЕСКАЯ МОДЕЛЬ ФРАКЦИОНИРОВАНИЯ СЫПУЧЕГО МАТЕРИАЛА МЕТОДОМ РАССЕВА

Описание исследуемого технологического процесса с физической точки зрения может быть сведено к следующей системе понятий и допущений, которые необходимы для обоснования рассматриваемой далее математической модели данного процесса.

• 1.    Исходный продукт, поступающий на сито, представляет собой механическую смесь частиц разной крупности.

• 2.    Соотношение размеров отверстий в сите и размеров частиц таково, что только часть материала остается на сите, а другая его часть проходит через отверстия. Соответственно, различают надрешетный продукт и подрешетный продукт, а каждая частица в зависимости от крупности может быть названа проходной или непроходной .

• 3.    Количество непроходных, проходных частиц и общее количество частиц в надрешетном продукте может быть выражено их массой. Объем древесной щепы определяют с учетом уплотнения или разрыхления массива древесных частиц [2].

• 4.    Количество проходных частиц в надрешетном продукте с течением времени уменьшается в процессе рассева.

• 5.    Количество непроходных частиц в надрешетном продукте остается постоянным в процессе рассева. Концентрация непроходных частиц в надрешетном продукте увеличивается в процессе рассева.

• 6.    Непроходных частиц в подрешетном продукте нет. Количество проходных частиц в подрешетном продукте возрастает в процессе рассева.

• 7.    Физико-механические свойства и геометрические параметры частиц фракционируемой смеси в процессе рассева не изменяются.

• 8.    Проходная частица, находящаяся в массиве надрешетного продукта, покидает надрешетный продукт, если достигает поверхности сита и попадает в отверстие. Требуемое для этого время зависит от толщины слоя надрешетного продукта, концентрации проходных частиц, формы отверстий и от других параметров. Предполагается, что на каждом достаточно малом отрезке времени A t

• 9.    Степень извлечения проходных частиц из надрешетного продукта равна отношению количества проходных частиц в подрешетном продукте к количеству проходных частиц в надрешетном продукте на старте процесса фракционирования.

уменьшение количества проходных частиц в надрешетном продукте пропорционально величине A t и количеству проходных частиц в надрешетном продукте в данный момент времени.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ФРАКЦИОНИРОВАНИЯ

Пусть в момент времени t _t = t количество непроходных частиц в надрешетном продукте равно Q_a . Количество проходных частиц в надрешетном продукте в тот же момент времени равно Q_b . Соответственно, общее количество частиц в надрешетном продукте равно Q = Q_a + Q b . Определим концентрацию непроходных и проходных частиц в надрешетном продукте:

Ca = Qa / Q, Cb = Qb / Q.(1)

A0 = A.(4)

T

Подставив (3) в (2), получим с учетом (1) и (4):

С

Ca +A Ca =---a— .

a a 1 -ACb

Перепишем равенство (5) в виде

(Ca +A Ca )(1 -A Cb ) = Ca(6)

или

Ca +A Ca - Ca A Cb -A Ca A Cb = Ca .

Предполагая, что A C_a и A C_b достаточно малы, и пренебрегая произведением A C_a A C_b , получим с учетом (3) соотношение A C_a = C_aAi 0 C_b , которое запишем в следующем виде:

= C a C b .                   (7)

В момент времени t , _{+ 1} = t + A t количество непроходных частиц в надрешетном продукте останется прежним, равным Q_a . Количество проходных частиц в надрешетном продукте уменьшится на величину A Q b и будет равно Q * = Q_b — A Q b . Соответственно, общее количество частиц в надрешетном продукте будет равно ^Q * = ^Qa ^{+ Q}b —A ^Qb = ^{Q -A Q}b . Определим ^концентрацию C_a = C_a + A C_a непроходных частиц в надрешетном продукте при t , _{+ 1} = t + A t :

Переходя в (7) к пределу при A0 ^ 0 и учитывая, что C_a + C_b = 1, то есть C_b = 1 - C_a , получим дифференциальное уравнение:

dCa" = C a (1 - C a ) - а У

C +A C = = ——— a a Q Q-A Qb

.

Анализ физического содержания моделируемой технологической ситуации позволяет сформулировать гипотезу, что величина A Q_b пропорциональна продолжительности отрезка времени A t и количеству проходных частиц в надрешетном продукте Q_b . Необходимо учитывать также производительность оборудования для данного фракционируемого материала. Пусть

A Q b = — Q b , (3)

T где T - неизменяющийся с течением времени параметр модели, зависящий от конструктивнотехнологических характеристик оборудования и физико-механических свойств фракционируемого материала. Параметр т имеет размерность времени и подлежит определению по результатам технологического эксперимента. Обозначим

Здесь d 0 = dt / т . Решение уравнения (8) найдем, используя, например, таблицы интегралов [3]. В итоге, учитывая, что на старте процесса фракционирования концентрация непроходных частиц в надрешетном продукте равна C_{a 0} , получим выражение для определения концентрации непроходных частиц в надрешетном продукте в зависимости от безразмерного параметра времени в = t / т .

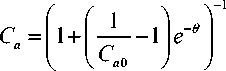
Выражение (9) может быть записано в следующем стандартном виде:

C =    Ca 0 ев a 1 + Caо(ев -1)

.

Уравнение (8) является частным случаем логистического уравнения, которое в 1838 году опубликовал бельгийский математик Ферхюльст (P. F. Verhulst) в связи с исследованием модели роста численности населения [12]. В настоящее время это уравнение, его модификации и обобщения часто используются при построении математических моделей в исследованиях биологических, экологических и экономических проблем. С тече-

нием времени область применений этого уравнения расширяется [10], [12]. Однако применений логистического подхода к построению моделей фракционирования сыпучего материала в известных нам публикациях, в том числе представленных в виде интернет-ресурсов, найти не удалось.

Для практического применения предлагаемой модели необходимо определить значение т . Принимая во внимание, что 9 = t / т , и используя равенство (10), получим следующее соотношение:

t

^Т = ln C a (1 - C a 0 ) . (11) C a 0 (1 — C a )

Параметр т может рассматриваться как некоторая технологическая константа. Для нахождения т (11) достаточно определить по результатам пробного рассева поступившей на переработку щепы концентрацию непроходных частиц в надрешетном продукте C_{a 0} на старте рассева и концентрацию C a при фиксированном времени t .

Установим физический смысл параметра т . Для этого примем t = т , то есть 9 = 1. Тогда из соотношения (10) следует, что

C a ₌ e

C a 0    1 + C a о ( e — 1).

Таким образом, т представляет собой отрезок времени, по прошествии которого концентрация непроходных частиц в надрешетном продукте увеличится в n раз, n = e/(1 + Ca0(e -1)) « 2,73 /(1 +1,73Ca0).

Обозначим: Cb0 - концентрация проходных частиц в надрешетном продукте на старте процесса фракционирования; Cb - концентрация проходных частиц в надрешетном продукте по прошествии некоторого времени t, Cb = 1 - Ca; Е - степень извлечения. Тогда в соответствии с приведенным выше определением степени из- влечения получим:

г -С    С С -С

- C b 0 C b        C b _ C a C a 0 C = -------- = 1--= -------- .

С C 1 -C

b 0                  b 0               a 0

НЕКОТОРЫЕ ЗАКОНОМЕРНОСТИ ПРОЦЕССА РАССЕВА1

Результаты применения предлагаемой методики (см. рисунок) согласуются с экспериментальными и расчетными данными, полученными по другим методикам [5], [9]. Разработанная модель дополняет класс однопараметрических моделей рассева, рассмотренных, например, в статье [8].

Воспользуемся разработанной моделью для анализа некоторых закономерностей исследуемого процесса фракционирования. Представленные на рисунке данные получены при моделировании трех технологических ситуаций, в каждой из которых фракционируется смесь с начальной концентрацией непроходных частиц в надрешетном продукте Ca0 , равной 0,10; 0,25; 0,50. При этом для рассева используется одно и то же оборудование, характеризуемое во всех рассмотренных случаях одним и тем же значением т = 16,14 с.

Наибольшая скорость рассева достигается, когда концентрация непроходных частиц в надрешетном продукте равна C_a = 0,50. Это состояние технологического процесса соответствует точке перегиба на кривой. Дальнейшее увеличение концентрации C_a происходит с уменьшающейся скоростью.

На кривой, построенной при C_{a 0} = 0,50, точка перегиба имеет место при t = 0. С уменьшением C_{a 0} точка перегиба сдвигается вправо и характер соответствующей логистической кривой на исследуемом интервале времени проявляется более четко.

Изменение начальной концентрации непроходных частиц от C_{a 0} до C_a ^*₀ приводит к сдвигу показанных на рисунке кри_* вых на величину t ^* по оси абсцисс. Значение t * определяется из соотношения 9 = t / т . Можно показать, что значение параметра сдвига 9* не зависит от времени и определяется только значениями начальной концентрации непроходных частиц в надрешетном продукте:

9* = ln

C a 0 (1 - C_a *0 )

СО - C a 0 )

При т * = т = 16,14 с получим t * = 17,73 с.

Соотношение (14) может быть использовано для прогнозирования качества продукции, затрат времени, энергии и других ресурсов на фракционирование в зависимости от гранулометрического состава сыпучего материала. При этом изменение параметра т позволяет учесть влияние конструктивных и технологических характеристик оборудования для рассева и оценить его эффективность.

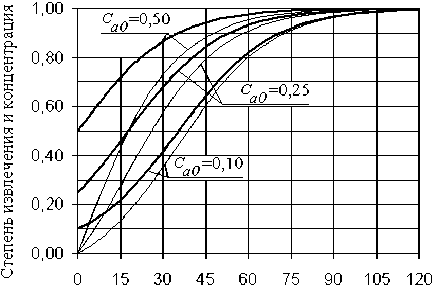
Продолжительность рассева, в секундах

Изменение Е (тонкие линии) и C a (утолщенные лини) в зависимости от C a ₀ и t

Рассмотренные закономерности дополняют результаты, известные в данной области прикладных исследований [8], [9], [11].

ВЫВОДЫ

Результаты решения модельных технологических задач с применением предлагаемой методики (см. рисунок) согласуются с известными данными, полученными другими методами.

Принципиальное отличие предлагаемой модели заключается в том, что она построена с применением логистического подхода. Применение логистического подхода позволило построить новую для затронутой области прикладных исследований модель, которая не является избыточно сложной по структуре, по составу и объемуисходных данных, по численной реализации. При этом обеспечивается степень адекватности, достаточная для практического применения при анализе закономерностей фракционирования сыпучих материалов методом рассева.

Появление логистического уравнения Фер-хюльста (8) в рассматриваемом случае также неслучайно и является вполне обоснованным с физической точки зрения. Действительно, адекватность математических моделей динамики популяций с учетом продолжительности жизни особей подтверждена многочисленными исследованиями [10], [12]. В нашем случае фракционирования сыпучего материала роль особи играет отдельная проходная частица. Массив про- ходных частиц играет роль популяции. «Продолжительность жизни» проходной частицы в массиве надрешетного продукта измеряется отрезком времени, в течение которого эта частица пройдет путь до поверхности сита и попадет в одно из отверстий сита. Эти аналогии служат дополнительным подтверждением адекватности предлагаемой модели фракционирования сыпучего материала.

Подходы, базирующиеся на применении логистического уравнения и его обобщений, эффективно применяются во многих других областях прикладных исследований, что подтверждает фундаментальный характер результата, полученного Ферхюльстом в виде данного уравнения и его применений [12]. Отражая внутреннюю логику развития прикладных исследований, выполняемых в затронутой области на основе методологии математического моделирования, предлагаемая модель фракционирования сыпучих материалов закономерно расширяет область продуктивного применения логистического подхода.

Адекватность построенной модели и небольшой объем исходных данных позволяют рекомендовать эту модель для использования при обосновании и оптимизации конструктивных и технологических параметров оборудования, предназначенного для фракционирования древесной щепы и других сыпучих материалов.

Работа выполнена при поддержке РФФИ (проект № 08-08-00979).

ПРИМЕЧАНИЕ

Данная часть работы выполнена при участии аспиранта А. В. Кульбицкого.