Локация силового воздействия индикаторным пьезоэлектрическим MDS-покрытием по информативным импульсам тока

ВЕСТНИК ПНИПУ. МЕХАНИКА № 6, 2024PNRPU MECHANICS BULLETIN

© Паньков Андрей Анатольевич - д. ф.-м. н., проф. кафедры механики композиционных материалов и конструкций, e-mail: ,

Andrey A. Pan’kov – Doctor of Physical and Mathematical Sciences, Professor, Department of Mechanics of Composite Materials and Structures, e-mail: ,

Актуальной задачей сенсорной техники является совершенствование сенсорных индикаторных и тактильных полимерных покрытий для индикации и количественной оценки действующих на протяженную, в частности, аэродинамическую поверхность внешних силовых воздействий в виде ударов града, бетонной крошки из-под переднего колеса при взлете самолета с взлетно-посадочной полосы, частиц космического мусора с целью мониторинга сохранения прочностных и аэродинамических характеристик элементов аэрокосмической техники. Гибкие полимерные тактильные датчики (покрытия) [1–3] широко используют для измерения механических воздействий (сил, давления) [4–7] и/или физических и геометрических характеристик (текстуры, формы) внешних объектов (окружающей среды) в результате непосредственного контакта объекта с тактильной поверхностью, в частности, в устройствах высокоинтеллектуальной электроники, интерфейсах взаимодействия человека и машины, электронной коже для «очувствления» робототехничеких устройств [8–13]. Для создания тактильных датчиков (покрытий) используются различные принципы функционирования: резистивные, емкостные, пьезоэлектрические, трибоэлектрические, оптические и магнитные, при этом каждый механизм имеет уникальные преимущества для конкретных применений. В современные тактильные покрытия встраиваются различные функциональные чувствительные, например, резистивные проводящие, пьезоактивные [14–18] и механолюминесцентные [19] элементы. В гибких тактильных покрытиях широко используются пьезоэлектрические полимерные поливи- нилденфторидные пленки PVDF [16–18]. Характеристики тактильных датчиков определяются их активным слоем, который непосредственно воспринимает диагностируемые физические и/или механические величины из внешней среды: давление, температуру и деформацию и преобразовывает их в различные оптические или электрические сигналы: ток, напряжение, сопротивление и емкость. Пьезоэлектрический активный слой [14– 18] функционирует через преобразование механической энергии в электрическую и, в результате, при внешнем силовом воздействии активным слоем генерируется информативный электрический заряд, величина которого пропорциональна значению измеряемой силы.

Широкое применение в различных областях науки и, в частности, аэрокосмической техники находят современные MFC-актуаторы (сенсоры) [20–22], которые состоят из композитного пьезоэлектрического слоя в виде близко уложенных в один ряд однонаправленных пьезокерамических (PZT-5A) волокон в полимерном (эпоксидном) связующем. На верхней и нижней поверхности пьезоэлектрического слоя установлены пленочные «встречно-гребенчатые» взаимодействующие электроды (IDE), расстояния между соседними разнонаправленными прямолинейными узкими тонкими полосками электродов 0,5 мм, при этом полная толщина такого пленочного MFC-актуатора 0,3 мм. Дополнительное улучшение рабочих характеристик MFC-актуатора возможно посредством использования монокристаллических пьезоэлектрических волокон [22] вместо традиционно используемых поликристаллических пьезоэлектрических волокон в композитном пьезоактивном слое актуатора. По аналогии с устройством MFC-актуатора в [23; 24] предложены мембранные (MDS) [23]

и цилиндрические (CDS) [24] пьезоэлектрические актуаторы (сенсоры) с двухзаходными, в частности: плоской или цилиндрической спиралями электродов, взаимодействующих через пьезоэлектрический слой (оболочку) с периодической взаимообратной поляризацией прослоек пьезоэлектрика между спиралями электродов. Способы: «скотч/нарезка» и «свертка развертки» изготовления MDS- и CDS-актуаторов(сенсоров) описаны в [25; 26] соответственно.

Цель исследования – разработка электромеханической математической модели формирования на встроенных электродах двойной спирали в круговой зоне возмущения индикаторного (сенсорного) пьезоэлектрического MDS-покрытия [23] информативных электрических импульсов напряжения при силовом воздействии – вдавливании в сенсорную поверхность покрытия жесткой шаровой частицы для диагностирования величины и локации эпицентра силового воздействия.

Электромеханическая модель индикаторного MDS-покрытия

Определим величину и форму измеряемого на активном сопротивлении R информативного k -го импульса электрического напряжения U_k ( t ), обусловленного действием силы P на внешнюю поверхность индикаторного MDS-покрытия (рис. 1) и, как следствие, действием соответствующего радиального давления p_k ( t ) на k -ю «пьезоячейку» – область пьезоэлектрика между парными дугами двойной спирали электродов внутри круговой зоны возмущения (деформирования) покрытия; величина давления p_k ( t ) находится с учетом удаленности k -й пьезоячейки от эпицентра силового воздействия (рис. 2, а , рис. 3, а ). Используем закон Гука с учетом пьезоэффекта

ε _k = ¹ σ _k + ^{e •} E_k ,                  (1)

c•c• где εk , σk=-pk – деформация и напряжение по радиальной координате ρ пьезоячейки, c• – модуль упругости пьезоэлектрика, e• – пьезоэлектрическая константа.

Возникающая при этом по радиальной координате ρ индукция электрического поля

D k =λ • E k + e • ε k                 (2)

создается не только из-за напряженности электрического поля E_k , но и благодаря пьезоэффекту, где λ _• – диэлектрическая проницаемость пьезоэлектрика. В результате подстановки выражения (1) в (2) индукцию запишем в виде

D k =λ • (1 + k e ²) E k - e ^• p k ,              (3)

c• где ke =e•/ λ•c• – коэффициент электромеханической связи пьезоэлектрика. Напряжение на обкладках (дугах электродов) пьезоячейки

U ( e ) k = E k δ ,                       (4)

где δ – расстояние между обкладками, т.е. соседними спиралями (дугами) электродов. На обкладках (– дугах электродов) пьезоячейки имеем поверхностную плотность зарядов

κ _k = q_k / S_k ,                       (5)

где q_k – величина электрического заряда, S_k = l_kh – площадь, l_k – длина дуги и h – ширина (равная толщине MDS-покрытия) обкладок.

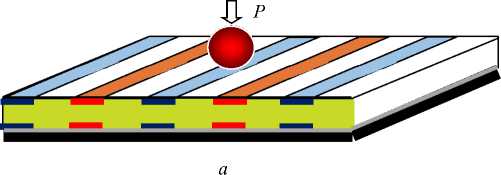
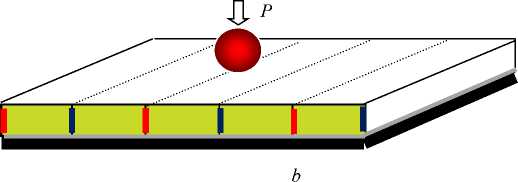
Рис. 1. Фрагменты индикаторного MDS-покрытия с поверхностной ( а ) и встроенной ( b ) двухзаходной спиралью ленточных электродов

Fig. 1. Fragments of indicator MDS-coating with surface ( a ) and built-in ( b ) double-lead spiral of tape electrodes

R

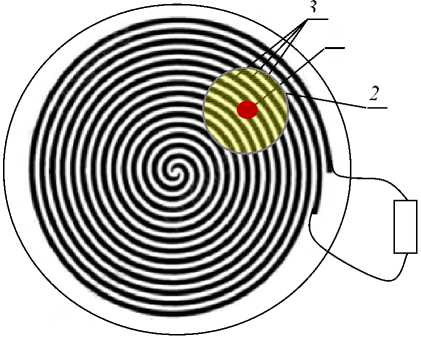
Рис. 2. Расчетная схема индикаторного MDS-покрытия со встроенными спиралями электродов при одиночном силовом воздействии, где 1 – эпицентр воздействия, 2 – зона возмущения (деформирования), 3 – дуги накачки (приема) пьезоэлектрических зарядов

Fig. 2. Design diagram of the indicator MDS-coating with built-in electrode spirals under single force impact, where 1 is the epicenter of the impact, 2 is the zone of disturbance (deformation), 3 are the pumping (receiving) arcs of piezoelectric charges

с

^C 1( k )

R

с

^Ce ( k )

^C 2( k )

R

а

b

Рис. 3. Элементарная пьезоячейка ( а ) и расчетная схема ее функционирования ( b ) в составе MDS-покрытия, где k – номер ячейки (дуги генерации электрических зарядов)

Fig. 3. Elementary piezocell ( a ) and design diagram of its functioning ( b ) as part of MDS coating, where k is the cell number (arc of electric charge generation)

Пьезоячейка (рис. 3) генерирует электрический ток величиной

таким образом, имеем

или в виде

I (e ) к =

dq =- S'd K dt dt

а          7 2_Ч dU_k e . .

- St ^ (1 + ке )-Т7---p к о dt

C •

= ^{( С} (1) к ^{+ С} (2) к ^{) U}k ⁺ „

R

dD _k

I ( e ) k      S dt S k

^x ^ (1 ⁺ k 2 ) ^d U

-

e_ dp k c , dt

с учетом D_k = к _k , (3), (4). Для расчетной схемы на рис. 3 выполняются равенства

¹ ( e ) к = ¹ (1) к ^{+ 1} (2) к ⁺ I ( R ) к , •

¹ (1,2) к = ^С (1,2) к^и (1,2) к ,                         ⁽⁷⁾

¹ ( R ) к = ^U ( R ) к / ^R ;

или в виде

(С(е)к + С(1)к + С(2)к Uк +    = e^ Spк,(8)

Rc где производные ик = dUk / dt, pк = dpk / dt, емкость пьезоячейки

С(е) к =К (1 + ке) у(9)

с учетом параллельного соединения ветвей замкнутой электрической цепи (рис. 3, b )

^U ( e ) k ^{= U} (1) k ^{= U} (2) k ^{= U} ( R ) k ^{≡ U}k

Дифференциальное уравнение (8) преобразуем к виду

U k + — U k = A k P k , ^τ * k

где постоянная времени разряда электрической цепи

τ*k=RС*k, коэффициент пьезоэлектрической связи

A k =

^e • ^Sk _, ^c • ^С * k

эффективная емкость

C * k - С ( e ) k + С (1) k + С (2) k =K I [ (1 + kbk + l - l k ]

или в виде

C * k =K ( l + k e l k ) h = hl ⁽ ^+ l p² 1       (11)

о о к l c• J с учетом равенства ke =e•/ λ•c• (3), здесь l – длина одиночной спирали электрода. Уравнение (10) связывает функцию Uk (t) регистрируемого выходного k-го импульса напряжения с приложенным к соответствующей k-й пьезоячейке давлением pk (t) с учетом пьезоэлектрических и геометрических характеристик индикаторного MDS-покрытия, удаленности пьезоячейки от эпицентра силового воздействия (рис. 3). Общее решение уравнения (10) известно [27]

(t,

U = e - */ T*\U(0) k + Ak J ePk (т) d т I,(12)

к            0

где U _{(0) k} – напряжение на обкладках пьезоячейки в момент начала действия давления p_k при t = 0; например, считаем, что U _{(0) k} = 0.

Для случая, когда давление p_k ( ξ _k , t ) изменяется вдоль локальной продольной координатной оси ξ _k ∈ ( - l_k /2; l_k /2) k -й пьезоячейки длиной l_k , тогда дифференциальное уравнение (10) преобразуется к виду

Uk + — U = Ak(Pk\

τ*k с общим решением

(               t)

Uk = e~t/" I U(0)k + Ak Je'/" {pk (т))lk dт I,(14)

к            0

где осредненное по длине k -й пьезоячейки значение давления

{^p bik = ^1/ l k J ^p k^dlk . l _k

Алгоритм локации эпицентра силового воздействия

Срединная линия составной сенсорной спирали «электрод/пьезоэлектрик/электрод» (рис. 4) имеет вид спирали Архимеда и в полярной системе координат ρ, φ описывается функцией

a

ρ= ϕ , 2 π

где a = 2 δ – шаг сенсорной спирали, δ – расстояние между соседними электродами по радиальной координате покрытия. Квазистатическое вдавливание жесткой шаровой частицы в точке А (см. рис. 2) обусловливает появление круговой области возмущения индикаторного покрытия, в которую входят n «дуг возмущений» на различных витках сенсорной спирали (рис. 4), на электродах которых генерируются электрические заряды.

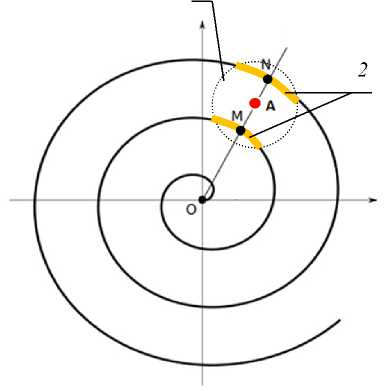
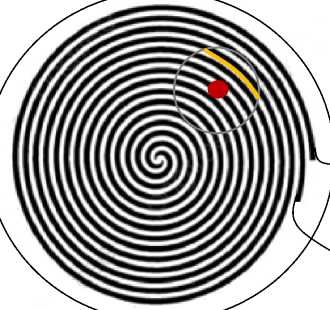
Рис. 4. Расчетная схема локации эпицентра силового воздействия в точке А , где спираль – срединная линия составной сенсорной спирали «электрод/пьезоэлектрик/электрод», 1 – контур зоны возмущения, 2 – активированные дуги сенсорной спирали

Fig. 4. Design diagram of the location of the epicenter of the force impact at point A, where the spiral is the midline of the composite sensor spiral "electrode/piezoelectric/electrode," 1 is the contour of the perturbation zone, 2 are the activated arcs of the sensor spiral

Считаем, что величина силового воздействия P такая, что значение радиуса Rε зоны возмущения равно или превышает шаг a сенсорной спирали. Выполнение этого условия обуславливает наличие как минимум двух дуг возмущений при произвольном положении точки А относительно соседних витков сенсорной спирали. Для случая, когда точка А равноудалена от сосед- них витков спирали имеем четное число n дуг возмущений, например, при n = 2 на втором и третьем витках сенсорной спирали (рис. 4). «Эпицентр» – точка А и локальные центры – точки M, N дуг возмущений расположены на едином полярном луче (рис. 4).

Число n дуг возмущений сенсорной спирали определяется значением силы P , шагом a сенсорной спирали и эффективными электроупругими свойствами индикаторного MDS-покрытия как спирально-армированного волокнистого полимерного композита [28]. Наличие n ≥ 2 дуг возмущений по длине сенсорной спирали обуславливает появление такого же числа n последовательных электрических импульсов напряжения, измеряемых на активном сопротивлении R (рис. 2), где t_k – время выхода k -го импульса, k = 1, n – номер импульса, τ _{k '} = t_{k ' + 1} - t_{k '} – временные интервалы между центрами последовательных импульсов, где k ' = 1, n - 1 – номер интервала. Длительности интервалов τ _{k '} между измеряемыми электрическими импульсами связаны пропорциональной зависимостью τ _{k '} =Δ _{k '}/ c с длинами Δ _{k '} k '-х «локационных» витков – спиральных отрезков сенсорной спирали, начало и конец каждого из которых – это центры k -й и ( k +1)-й дуг возмущений, где c – скорость распространения электрических импульсов в электродах. Начала и концы всех локационных витков лежат на едином полярном луче, проходящем через искомый центр силового воздействия в точке А (рис. 4). Длины Δ _{k '} локационных витков рассчитываем по формуле

Δ _{k '} = l ( ϕ _{k ' + 1}) - l ( ϕ _{k '}) ≈ a ( π+ϕ _{k '}), (17)

где ϕ _k , ϕ _{k + 1} = ϕ _k + 2 π – полярные углы центров k -й и последующей ( k +1)-й дуг возмущения сенсорной спирали, длина отрезка спирали

l ( ϕ ) =

2ПI у 7^2+1+2ln (ф+д/ф2^1 )

от полюса до точки с полярным углом φ, где 0<φ<2π k max , k max – полное число витков сенсорной спирали. Величина относительной погрешности линейной аппроксимации Δ k ’ ≈ a (π+φ k ’ ) (17) монотонно убывает от значения ≈7 % на первом, 3 % на втором витках до ≈ 0,028 % уже на пятом витке спирали.

В результате локацию точки А – эпицентра зоны возмущения от силового воздействия P осуществляем через вычисление ее полярных координат

ρ • =

c τ _•

2 π

cτ ϕ• = • a

по измеренному значению интервала времени τ• между двумя максимальными по величине соседними электрическими импульсами из середины регистрируемой на активном сопротивлении R последовательности электрических импульсов. Решение (18) получено с учетом, что длина Δ• = 2πρ• локационного витка сенсорной спирали между точками M и N (рис. 4) равна длине окружности, проходящей через точку А – середину прямолинейного отрезка MN, где ρ• – искомая радиальная координата точки А. При этом величина Δ• = сτ• вычисляется по измеренному значению τ•, а величина φ• – по уравнению спирали (16) с использованием найденного значения ρ• (18). По количеству и величине регистрируемых электрических импульсов на активном сопротивлении R делаем оценку величины P силового воздействия (см. рис. 1). Отметим, что решение (18) получено для случая, когда точка А расположена на равном удалении от соседних витков сенсорной спирали, т.е. посередине прямолинейного отрезка MN на рис. 4 и, как следствие, выполняется равенство Δ•=2πρ•. Таким образом, локация силового воздействия P по решению (18) удобна для практического применения, при этом точность локации улучшается с уменьшением шага a сенсорной спирали относительно радиуса Rε зоны возмущения при увеличении числа витков спирали.

Результаты численного моделирования

Рассматривалось круговое индикаторное пьезоэлектрическое MDS-покрытие радиусом R _* = 1 м и толщиной h = 5 мм для случая вдавливания жесткой шаровой частицы радиусом R _о =5 мм силой P = 1Н в точке (эпицентре зоны деформирования) с полярными координатами 0, 6 R _* , π /3. Спиральные ленточные электроды шириной h расположены по толщине слоя, расстояние (по радиальной координате покрытия) между соседними электродами 8 = 0,3 R, длину одиночной спирали (пьезоэлектрического элемента, рис. 3, а ) рассчитывали по формуле l ≈ π R _*² / δ . Длины хорд l k , удаленных на расстояния Δ k от эпицентра круговой зоны возмущения радиусом R _ε = k _ε P , рассчитываем по формуле l_k = 2 R _ε ² -Δ _k ², где коэффициент пропорциональности k _{ε R = 5мм} ≈ 0,006 м/Н при значении радиуса жесткой шаровой частицы R _о = 5 мм, модуле упругости c • = = 115 ГПа, пьезоэлектрической константе e _• = 15,1 Кл/м² и относительной диэлектрической проницаемости λ _• / λ ₀ = 635 пьезоэлектрика (PZT-4), где константа λ ₀ ≈ 8.85 ⋅ 10 ^{- 12} Ф/м. Величина активного сопротивления R = 0,1 Ом (см. рис. 2, 3).

На рис. 5 дано неоднородное распределение напряжения σk = -pk(ξ) по продольной координате ξ различных k-х дуг (хорд) круговой зоны возмущения индикаторного MDS-покрытия (рис. 5, b), обусловленной вдавливанием шаровой частицы силой P = 1Н (рис. 5, а) с учетом заданных упругих характеристик покрытия, где k = 1,7 с учетом k=1, 7 (□), 2, 6 (◊), 3, 5 (Δ) и 4 (○). Осредненные значения давления pk lk и ее производной РрkY в момент времени t е (0;10) по каждой из хорд рассчитывали по формулам

(Pk\t =Х(t)Рк, pkк\ =х(t)Рк, где t0 = 1 мкс – длительность импульса нагружения (квазистатического вдавления шаровой частицы), осредненные по каждой из хорд значения pk = 1,072,

0,902, 0,695, 0,489 [МПа] соответственно при А / R = 0, 0,3, 0,6, 0,9 с учетом возможных значений отношения А / R _о е (0;1.2). Пунктиром на рис. 5, b , отмечено заданное «пренебрежимо малое» (10 % от p _max ) значение давления p _min на границе (окружности) круговой зоны возмущения радиусом R _ε . На активном сопротивлении R вычисляем последовательность из 7 информативных импульсов U_k электрического напряжения (рис. 6, b ), где k = 1,7 с учетом k = 1, 7 (□), 2, 6 (◊), 3, 5 (Δ) и 4 (○).

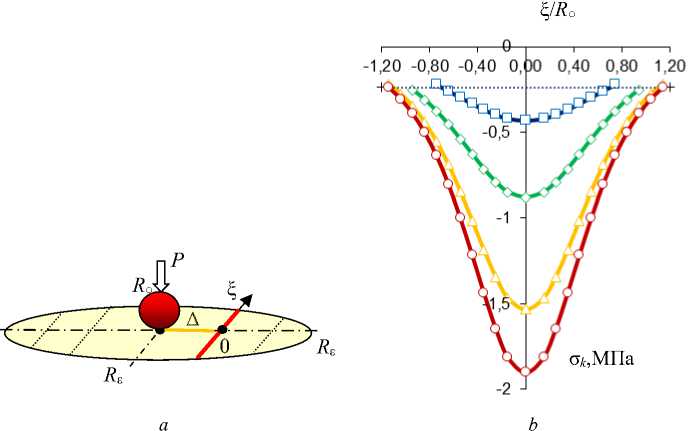
Рис. 5. Круговая зона деформирования покрытия от вдавливания шаровой частицы силой P ( а ) и распределение напряжения σ k (ξ) по к -м дугам (хордам) этой зоны ( b ) при А / R° = 0 (о), 0,3 (Л), 0,6 (◊), 0,9 (□), где Л, ( - локальные координаты хорд

Fig. 5. Circumferential zone of coating deformation due to impact of the ball particle by force P ( a ) and distribution of stress σ k (ξ) along к -th arcs (chords) of this zone ( b ) at А / R° = 0 (о), 0.3 (Л), 0.6 (◊), 0.9 (□), where Л, ( are local coordinates of chords

p _k , МПа

а

U k ,мВ

0,2

0,15

0,1

0,05

-0,05

t / t ₀

b

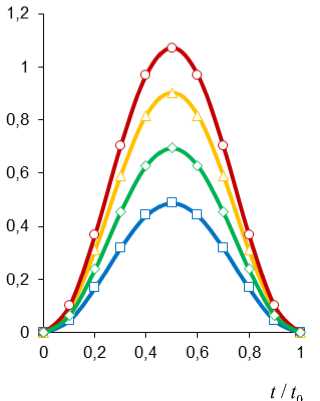
Рис. 6. Распределения давления p _k ( а ) и соответствующего ему импульса информативного электрического напряжения U_k ( b ) для к -й хорды при А / R ° = 0 (о), 0,3 (Л), 0,6 (◊), 0,9 (□)

Fig. 6. Distribution of pressure p _k ( a ) and corresponding pulse of informative electric voltage U_k ( b ) for k -th chord at А / R = 0 (о), 0.3 (Л), 0.6 (◊), 0.9 (□)

Заключение

Разработана электромеханическая математическая модель формирования на встроенных электродах двойной спирали в круговой зоне возмущения индикаторного пьезоэлектрического MDS-покрытия (см. рис. 1–5) информативных электрических импульсов напряжения U_k (14) (см. рис. 6, b ) при силовом воздействии – вдавливании в сенсорную поверхность покрытия силой P жесткой шаровой частицы для диагностирования величины и локации эпицентра (см. рис. 4) силового воздействия. Форма и длительность информативных электрических импульсов (см. рис. 6, b ) определены по виду