Локальная диагностика электрических цепей

Известные методы диагностики электрических цепей, рассмотренные в работах Бутырина П.А., Васьковской Т.А. и др., предполагают, что все параметры электрической цепи не известны. Это связано с тем, что при длительной эксплуатации оборудования параметры меняются, что может приводить к неисправности данного участка цепи. Также нужно заметить, что в реальных установках какие-то параметры цепи более подвержены повреждениям, какие-то менее. Предлагаем рассмотреть случай, когда для схемы, представленной на рис. 1, параметры двух ветвей из восьми известны. Наша задача - определить параметры оставшихся ветвей. Такой вид диагностики назовем локальной диагностикой. Применение локальной диагностики при исследовании электрической цепи позволяет уменьшить расчеты приблизительно в четыре раза.

При исследовании электрической цепи рассмотрим так называемый метод главных величин, а именно метод напряжений главных сечений и метод главных контурных токов.

Метод напряжений главных сечений основан на формировании такой системы уравнений по методу напряжений сечений, в которой удается выделить нулевую подматрицу максимальных размеров. Это позволяет исключить соответствующую часть напряжений сечений и получить уравнения для части напряжений сечений, названных главными.

В методе напряжений главных сечений используются следующие принципы:

• 1)    исходными для получения уравнений по методу напряжений главных сечений являются особые уравнения по методу напряжений сечений;

• 2)    в выражении напряжений ветвей через напряжения сечений (напряжения ветвей дерева) и в уравнениях по первому закону Кирхгофа используются разные системы независимых сечений;

• 3)    каждая система сечений состоит из двух подсистем - главной и дополнительной.

Будем считать, что системы независимых сечений выбираются с помощью деревьев t 1 и 1 ₂. Дерево t 1 служит для выбора сечений, для которых напряжения ветвей выражаются через напряжение ветвей дерева равенством

U - Q t U д .

Дерево t ₂ служит для выбора сечений, служащих для записи уравнений по первому закону Кирхгофа:

Q'I = 0 .

Дополнительные сечения должны удовлетворять следующим требованиям:

1) дополнительные сечения для двух систем сечений должны образовывать пары (парные сечения), то есть каждому дополнительному сечению одной системы должно соответствовать дополнительное сечение другой системы, имеющее с первым одну общую ветвь;

2) дополнительные сечения первой системы не должны иметь других общих ветвей с дополнительными сечениями второй системы, кроме общих ветвей парных сечений.

В качестве примера выберем деревья и сечения для графа на рис. 1.

Предположим, что E ₂ - 0, тогда при известных параметрах первой и восьмой ветви, зная матрицу для R ₂ :

R 2 =

r 1

r 8

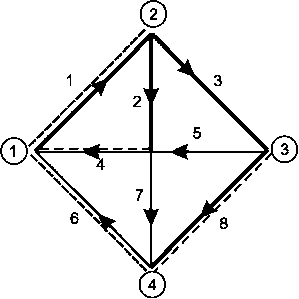
Рис. 1

замерив напряжения на второй и третьей ветви (опыт проводиться два раза), т.е. зная матрицу на-

пряжений первого дерева:

U

- U 21

^{1 д} "  L u 31

^U 22

U 32 J ’

а также замерив напряжения общих ветвей (также два раза):

U

2 -

U 11

U ₈₁

U ₁₂

U ₈₂

по известным параметрам легко определить матрицу проводимостей:

G 21 —R 2 ^{- 1} (U 2 - R 2 ■ J с 2 ) U 1 д ^{- 1}-      (9)

С другой стороны, для схемы, представленной на рис. 1, матрицу проводимостей можно записать:

Дерево t ₁ будем изображать толстой линией, а дерево 1 ₂ - пунктирной. Получим две системы сечений. Первая система определяется деревом t ₁ ,

G

21 ^-

^- g 2

g 5

^- g 3

^{- g} 35

Таким образом, можно определить проводимости второй, третьей и пятой ветви, т. е. g 5 , g 3 и

вторая – деревом t ₂

Составим для этой цепи уравнения по методу напряжений сечений, заменив предварительно ветви 1 и 8 по теореме о компенсации идеальными источниками тока, ток которых равен току ветви.

По обычным правилам метода напряжений сечений получаем матричное уравнение:

	2	3        1 8
4`	- g 2457	g 57     - g 4     g 7 1 Г U 2
6`	g 57	- g 3567   - g 6   - g 67   ■ U 3 =
1`	- g 2	- g 3        0      0       U 1
8`	g 5	- g 35        0      0 J L U 8 _
		J 4 - J 2 - J 5 + J 7
		- J 6 - J 7 + J 5 - J 3             m -    ( - J 2 - J 3 ) - 1 1    .            (1)
		L ( J 5 - J 3 ) - 1 8 J

В результате получаем нулевую подматрицу в матрице коэффициентов, то есть уравнение (1) имеет в общем случае следующую структуру:

g 2 , учитывая, Что g 2 ^- g 23 ^- g 3 .

Записав подобные уравнения для дерева и сечения графа на рис. 2, можно также определить проводимости четвертой, шестой и седьмой ветви при известных параметрах первой и восьмой.

По обычным правилам метода напряжений сечений получаем матричное уравнение:

4	6	1	8
3' Г - g 24	- g 36	- g 23	- g 3 1 Г u 4 "
5 - g 2457	g 57	- g 2	g 5 ■ u 6
1' - g 4	- g 6	0	0 U 1
8' L g 7	- g 67	0	0 J L U 8 J

Г J 3 + J 2 - J 4 - J 6 1
-	J 5 + J 2 - J 4 - J 7 - j 4 - j 6 - 1 1	J J .                     (11)
	L   - J 6 + J 7 - 1 8 J	J

Полагая, что E ₂ - 0 при известных параметрах первой и восьмой ветви, матрица для R ₂ ос-

1' G11

U 1^g ₌ J d

U 2 J L J c 2 - 1 2

тается та же.

Это уравнение можно записать в виде двух уравнений:

Замеряя напряжения на четвертой и шестой ветви (опыт проводиться два раза), будем знать матрицу напряжений первого дерева:

GuUu+G12 u 2 - Jc 1;(3)

G 21U1g = J с 2 -12.(4)

Из последнего уравнения

12 = J с 2 - G 21U1g -(5)

В уравнении (3) вектор напряжений общих ветвей можно заменить выражением по закону Ома:

^и 1д =

U ₄₁

U 61

U ₄₂

U ₆₂

Теперь, по известным параметрам определяем матрицу проводимостей для графа 2.

С другой стороны для схемы, представленной на рис . 2, матрицу проводимостей можно записать как

G 21 =

^- g 4

g 7

^- g 6

^{- g} 67

U 2 = R 2 1 2 - E 2 = R 2 ( J с 2 - G 21 U 1g ) — E 2 -  (6)

Таким образом, можно определить g 4 , g 6 и g ₇ .

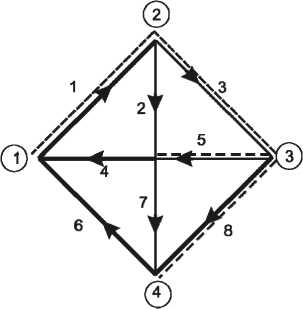
Рис. 2

3) главные контуры не должны содержать общих ветвей парных контуров.

Согласно этим требованиям дополнительные контуры двух систем заведомо различны. Подсистемы главных контуров могут совпадать.

Общие ветви парных контуров для краткости будем называть в дальнейшем просто общими ветвями.

В качестве примера выберем контуры, удовлетворяющие приведенным выше требованиям, для цепи на рис. 3. Сначала выберем пары дополнительных контуров. Здесь можно выбрать две пары контуров - контуры 3 и 3‘, имеющие общую ветвь 7, и контуры 4 и 4', имеющие общую ветвь 2.

В методе контурных токов исходными уравнениями, кроме уравнений по закону Ома, являются уравнения, выражающие токи ветвей через контурные токи:

I - B t I k                   (14)

и уравнения по второму закону Кирхгофа:

BU - 0 .               (15)

В уравнениях (14) и (15) использовалась одна и та же матрица контуров В . Однако это не является обязательным. В уравнении (15) можно использовать другую матрицу контуров B ' для другой системы независимых контуров, то есть уравнение (2) можно заменить уравнением

B ' U - 0 .                (16)

Уравнение по методу контурных токов в этом случае примет вид

B ' RB t I k - B ' E ,            (17)

где матрица контурных сопротивлений

Rk - B'RBt, а матрица контурных э.д.с.

E k - B ' E .

Согласно этим формулам строки матриц R _k и E k соответствуют одной системе контуров ( B ' ), а столбцы матрицы R _k - другой системе ( В ).

В методе главных контурных токов системы контуров, соответствующие матрицам В и B ' , выбирают так, чтобы можно было исключить часть контурных токов.

Каждую систему независимых контуров разделяем на две подсистемы. Первая подсистема контуров называется главной и содержит группу главных контуров. Вторая подсистема содержит дополнительные контуры.

Дополнительные контуры двух систем контуров должны удовлетворять следующим требованиям:

• 1)    должны образовывать пары (парные контуры), то есть каждому контуру одной системы должен соответствовать парный ему контур другой системы, имеющий с первым только одну общую ветвь;

• 2)    не должны иметь других общих ветвей с дополнительными контурами второй системы, кроме упомянутых выше общих ветвей парных контуров;

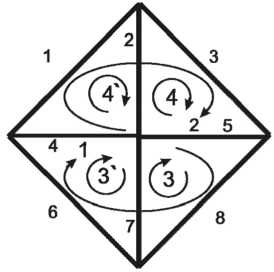
Рис. 3

Главные контуры не должны содержать общих ветвей 2 и 7, поэтому мысленно удаляем эти ветви и в оставшейся цепи выбираем 2 независимых контура 1 и 2. Получаем две системы контуров: 1, 2, 3, 4 и 1, 2, 3', 4'. Первая подсистема главных контуров (1,2) одинакова для обеих систем независимых контуров. Вторые подсистемы - раз-

личны.

Используя обычные правила метода контурных токов, для цепи на рис. 1 получаем уравнение

• 1   r4568   - r45    r58

• 2    - r45    r1345 - r5

3'    r64     - r4    00

4'[ - r4     r41     00

E 1

E 2

E ₃ - U ₇

E ₄ - U ₂

I_{k 1}

^I k 2

^I k 3

I_{k 4}

В результате получаем нулевую подматрицу в матрице коэффициентов, то есть уравнение (18) имеет в общем случае следующую структуру:

1`

2`

_{R 1} k ₁

R k

Rk

^I k 1

I ₂

^E k 1

. E k 2 - U 2

Для краткости записи приняты обозначения типа r ₄₅₆₈ - r ₄ + r ₅ + r ₆ + r ₈. Аналогично для других контурных сопротивлений. Строки матриц уравнения (18) соответствуют контурам 1, 2, 3', 4', а столбцы - контурам 1, 2, 3, 4.

Это уравнение можно записать в виде двух уравнений:

Rk 'Ik 1 + R^ = Ek 1;

Rkilki = Ek2 - U2.(21)

Из последнего уравнения:

U = Ek2 - Rkilk 1.(22)

В уравнении (20) вектор тока можно заменить выражением по закону Ома:

I k 2 = G 2 U 2 - J 2 = G 2 ( E k 2 - R k 1 I k 1 ) — J 2 . (23)

Предположим, что J ₂ = 0 , тогда при известных параметрах седьмой и второй ветви знаем матрицу для проводимостей G ₂ :

1	2	3	4
1    r 4568	~ r45	r 64	- Г 4      I k 1          E 1 Г 41      I k 2 _ E 2      . (30)
2 - r 45	r 1345	~ r4
3      r 58	~ r5	0	0      I k 3       E 3 - U 7
4' L - r 5	r 35	0	0     I k 4      E 4 - U 2

Полагая, что J ₂ = 0 при известных парамет -рах второй и седьмой ветви, матрица для G ₂ оста-

ется та же.

Замеряя токи третьей и восьмой ветви (опыт проводится два раза), будем знать матрицу токов:

^I k 1 ⁼

^I 31

I ₈₁

I ³² .

82 J

G 2 =

g 7 0

0 g 2

Замерив токи в первой и шестой ветви (опыт проводиться два раза), определяем матрицу токов

Теперь по известным параметрам определяем матрицу сопротивлений R ₂₁ .

С другой стороны, для схемы, представленной на рис.4, матрицу сопротивлений можно записать как

^I k 1 ⁼

I ₁₁

L 1 61

I ₁₂

1 62 J

R 21 = _^r 5 ⁸    _r r⁵              (32)

L ^r 5      ^r 35 ^J

и замерив токи общих ветвей, т. е. токи во второй и седьмой ветви (также два раза), получаем

^I 2 ⁼

^I 21

I ₇₁

^I 22

I ₇₂

.

При этом напряжения на этих ветвях известны:

^E k 2 ⁼

^E 21

E ₇₁

^E 22

Тогда по известным параметрам легко рассчитать матрицу сопротивлений:

R 21 = - G 2 ^{- 1} (I 2 - G 2 E k 2 ) I k f¹ .     (28)

С другой стороны, для схемы, представленной на рис. 3, матрицу проводимостей можно записать как

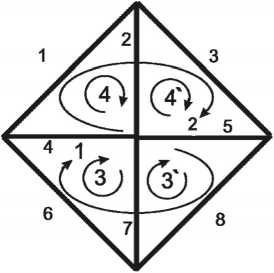
Рис. 4

^r 64   ^{- r} 4

^{- r} 4     ^r 41

Таким образом, сопоставляя полученные ре- зультаты, можно легко определить сопротивления первой, четвертой и шестой ветви, т. е. r1, r4 и r6 , учитывая, что r1 = r41 - r4 и r6 = r64 - r4.

Записав подобные уравнения для цепи на рис. 4, можно также определить сопротивления третьей, пятой и восьмой ветвей при известных параметрах первой и восьмой.

По обычным правилам метода напряжений сечений получаем матричное уравнение:

Таким образом, сопоставляя значения, можно определить r 3 , r 5 и r 8 .