Локальная микроструктура метастабильного состояния. Переохлажденный пар
Автор: Аграфонов Ю.В., Ваганова Т.Г., Цыдыпов Ш.Б., Нестеров А.С., Просекин М.Ю., Просекина И.Г., Петрушин И.С.
Журнал: Вестник Бурятского государственного университета. Философия @vestnik-bsu
Рубрика: Физика и техника
Статья в выпуске: 6, 2007 года.
Бесплатный доступ
Модифицированное уравнение Орнштейна-Цернике применено для описания локальной микроструктуры метастабильного состояния (переохлажденный пар). Вычисления проведены с точностью до квадратичных членов по степеням плотности. Межмолекулярное взаимодействие задается потенциалом Лен-нард-Джонса. Показано, что локальная микроструктура выражена более резко, чем в термодинамически равновесном паре.
Короткий адрес: https://sciup.org/148178190
IDR: 148178190
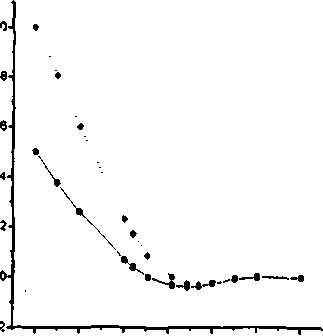
Список литературы Локальная микроструктура метастабильного состояния. Переохлажденный пар
- Нестеров А.С., Сандитов Д.С., Цыдыпов Ш.Б., Аграфонов Ю.В., Парфенов А.Н. Описание стеклообразного состояния простых молекулярных систем с помощью уравнения ОрнштейнаЦернике//Журн. физической химии. -Т. 80, № 5. -2006.
- Аграфонов Ю.В., Нестеров А.С., Цыдыпов Ш.Б. и др. Модификация уравнений ОрнштейнаЦернике для аморфных состояний//Ультразвук и термодинамические свойства вещества. -2003. -№29. -С. 120.
- Аграфонов Ю.В., Нестеров А.С., Цыдыпов Ш.Б. и др. Использование модифицированного уравнения Орнштейна-Цернике в области аморфных состояний вещества//Вестник Бурятского госуниверситета. -Сер. 9: Физика и техника. Вып. 3. -Улан-Удэ: Изд-во Бурятск. госун-та, 2004. -С. 69..
- Martynov G.A. Exact equations and the theory of liquids. I Analysis. Transformation and method of solving exact equations//Molecular Physics. -1981. -Vol. 42.-No 2.-Pp. 329.
Статья научная
