Локальная покомпонентная асимптотическая эквивалентность и её применение к исследованию устойчивости по части переменных

Введение. Классификация множества систем обыкновенных дифференциальных уравнений и ее применение к исследованию устойчивости решений восходит к А. М. Ляпунову [1]. В случае, когда исследуется асимптотическое поведение решений при t ^+w , классификация носит название асимптотической эквивалентности [2-4]. Основные результаты исследования подобных отношений отражены в работах [2-18]. В работах [1113] для классификации нелинейных систем введены понятия покомпонентной асимптотической эквивалентности по Брауеру и Левинсону относительно некоторых функций.

В настоящей работе продолжается развитие идей Е. В. Воскресенского [13] о покомпонентной асимптотической эквивалентности по Брауэру и Левинсону относительно некоторых функций нелинейных систем в некоторой области фазового пространства. Показано, что введенные определения позволяют исследовать устойчивость по части переменных и асимптотику решений более широкого класса нелинейных систем, чем в работах [11-13].

В качестве приложения рассмотрена математическая модель брутто-реакции пиролиза этана. Положение равновесия исследуемой системы исследовано на устойчивость по части переменных, а также найдена асимптотика решений в окрестности положения равновесия.

Локальная покомпонентная асимптотическая эквивалентность по Брауэру и Левинсону. Рассмотрим множество Е всех систем обыкновенных дифференциальных уравнений вида dx dt

^{f (} t , ^x ) ,

где x е R n , f е C ⁽⁰’¹⁾( [ T , +^ ) x R ⁿ , Rⁿ ), T >  0 , f ( t ,0) = 0 .

Будем считать, что у системы вида (1) существует совокупность решений x ( t : t ₀, x ⁽⁰⁾) , определенных при всех t >  t ₀ >  T и x ⁽⁰⁾ е D ^ Rⁿ , где D - некоторая область пространства Rⁿ , содержащая окрестность нуля.

Обозначим через x(t: t0, x(0)) и y(t: t0, y(0)) решения с начальными данными (t0, x(0)) и (to, У(0)) соответственно системы дифференциальных уравнений (1) и системы dy = g(t, У),                                        (2)

dt

принадлежащей множеству Е .

Следующие определения развивают идеи Е. В. Воскресенского о покомпонентной асимптотической эквивалентности по Брауеру относительно функций ц ( t ) из работ [11-13].

Определение 1. Системы обыкновенных дифференциальных уравнений (1) и (2) назовем локально асимптотически эквивалентными по Брауэру относительно функции ц (t), если при фиксированном t0 > T существуют два отображения P(1) : V > U и P(2) : U > V такие, что

X i (t : t о , x ⁽⁰⁾) = у , (t : 1 ₀, P ⁽²⁾ x ⁽⁰⁾) + o ( ц , (t)) ,                               (3)

y_t^{(t :} t 0 , y ⁽⁰⁾) = ^xi^{(t :} t 0 , P 1) y ⁽⁰⁾) ^{+ o (} ц i^(t )) ,                              ⁽⁴⁾

при t ^® для всех i e M _o c {1,..., n} . Здесь x ( t : t ₀, x ⁽⁰⁾) , y_i ( t : t ₀, y ⁽⁰⁾) - i - ые компоненты решений, для которых x ⁽⁰⁾ e U, y ⁽⁰⁾ e V , U , V c D - некоторые области, содержащие окрестность нуля, ц : [ T , +ад )   >  [0, +ад ) .

Определение 2. Если в определении 1 положить М_о = {1,..., п} , то системы (1) и (2) будем называть локально асимптотически эквивалентными по Брауеру относительно функций ц ( t ).

Замечание 1. Определение 2 обобщает определение локально асимптотически эквивалентных систем по Брауеру относительно функции ц ( t ) из работы [13]. Для этого достаточно в определении 2 положить ц ( t ) ^ ц ( t ), i = 1, n .

Определение 3. Если в определении 1 положить P ⁽²⁾ = P ⁽¹⁾ , то системы (1) и (2) назовем локально покомпонентно асимптотически эквивалентными по Левинсону относительно функций ц ( t ). Если же кроме этого М_о = {1,..., п } , то системы (1) и (2) назовем локально асимптотически эквивалентными по Левинсону относительно функций Ц , ⁽ t ) .

Определение 4. Будем говорить, что система (1) имеет локальное асимптотическое равновесие по компонентам i e Mo c {1,.-.,n}, если каждое ее решение x(t: t0, x(0)), x(0) e U c Rn, обладает свойством lim x (t: t0, x(0)) = b < ад, i e Mo,                           (5)

t >+ад и, наоборот, для любых чисел b,i e Mo, таких, что b = colon(b,...,bn) e V c D , существует решение x (t: t0, x(0)) , x(0) e U c D, системы (1) такое, что справедливо равенство (5).

Определение 5. Если в определении 4 положить M_Q = {1,..., n } , то будем говорить, что система (1) имеет локальное асимптотическое равновесие.

Сформулируем достаточные условия, когда локальные покомпонентные асимптотически эквивалентные по Брауэру системы сохраняют свойства устойчивости и асимптотической устойчивости по части переменных.

Теорема 1. Пусть системы (1) и (2) локально покомпонентно асимптотически эквивалентны по Брауэру относительно функций ц_; ( t ), причем отображения P ⁽¹⁾ и P ⁽²⁾ являются непрерывными в нуле и справедливы равенства

X i (t : 1 ₀, x ⁽⁰⁾) = y i (t : 1 ₀, P²⁾x ⁽⁰⁾) + ц (t )5 i (t : t ₀, x ⁽⁰⁾),                    (6)

У ^{( t :} t о , У ⁽⁰⁾) = x ^{(t :} t o , ^{P (1)} У ⁽⁰⁾) ⁺ M i-^(t ) Y , ^{(t :} t о , У ⁽⁰⁾) ,                   ⁽⁷⁾

где 5г (t: t0,x(0)) и у.(t: t0,y(0)) стремятся к нулю при t —+х равномерно по x(0) и у(0), соответственно. Тогда, если у одной системы существует устойчивое (асимптотически

( lim ц = 0 ) , \ t —+®       /

устойчивое) тривиальное решение по компонентам i е Мо и lim ц = dt, d е R1 t —>+ю то вторая система имеет также устойчивое (асимптотически устойчивое) тривиальное решение по компонентам i е Мо; кроме того, если одна система имеет локальное асимптотическое равновесие по компонентам i е Мо и lim ц = dt, di е R1 то этим же t —IX свойством будут обладать и решения другой системы.

Доказательство. Доказательство проводится аналогично доказательству 1.6.6 из работы [13, с. 50].

Пусть система (2) обладает устойчивым (асимптотически устойчивым) тривиальным

( lim ц = 0 ) . Сопоставим начальным \ t —+х ¹     /

решением по компонентам i е Мо и lim ц = d,, d( е R1 t ——+X значениям у е V решений системы (2) начальные значения x = P(1) у соответствующих решений системы (1).

Тогда, учитывая равенства (6), получим

I x i ^{( t :} t 0 , ^x )|| ^ || y i ^{( t :} t 0 , ^y )|| ⁺ M i ⁽ t ^{) 5} i ^{( t :} t 0 , ^x ) ,                                ⁽⁸⁾

где y = P ⁽²⁾ x .

Пусть || y || <  ^ . Тогда из непрерывности отображения P ⁽¹⁾ в нуле следует

I- x =| | P‘¹¹ y || <  s .

С учетом оценки (8) из устойчивости тривиального решения системы (2) по компонентам i е Mo и того, что 5, (t: t0, x) — 0 при t —+x равномерно по x следует устойчивость тривиального решения системы (1) по компонентам i е Мо, а из асимптотической устойчивости тривиального решения системы (2) по компонентам i е Мо следует асимптотическая устойчивость тривиального решения системы (1) по компонентам i е Мо.

Пусть решения системы (2) при у(0) е V имеют асимптотическое равновесие по компонентам i е Мо. Это означает, что lim у (t: tо,у(0)) = bt, b е R1.

t ^+ж

Из оценки (8) получаем lim

x_{ (t : t о , x ⁽⁰⁾) - у ( t : t о , P ^<2) x ⁽⁰⁾)

t ^+®

Н i ⁽ t )

= 0 , i е M о ,

и, следовательно, справедливы равенства (5).

Покажем теперь, для любых чисел b , i е M^ , таких, что b = colon(b ,..., b_n ) е V c D , существует решение x ( t : t ₀, x ⁽⁰⁾), x ⁽⁰⁾ е U c D , системы (1) такое, что справедливо равенство (5). Для фиксированных чисел b , i е M_o , b = colon ( b ,..., b_n ) е V c D , найдем компоненты у ( t : t ₀, у ⁽⁰⁾) решения системы (2) такие, что справедливы пределы (9). Учитывая (10), получаем справедливость равенств (5), и, следовательно, система (1) имеет локальное асимптотическое равновесие по компонентам i е М _о.

Доказательство устойчивости (асимптотической устойчивости) тривиального решения системы (2), когда известно, что тривиальное решение системы (1) – устойчиво

(асимптотически устойчиво), проводится аналогично на основании равенства (7). Доказательство завершено.

Исследование асимптотики поведения решений системы дифференциальных уравнений математической модели брутто-реакции пиролиза этана.

Рассмотрим брутто-реакцию пиролиза этана [19–21]:

C₂H₆ ^ C₂H₄ + H₂ 2C₂H 6 ^ C 2 H 4 + 2CH 4

Математическая модель реакции имеет вид:

c = - k_xc_x - 2 k₂c²

c₂ = k_xc_x + k₂c 2

c3 = kxcx c 4   2 k2 c| здесь t > 0, c (i = 1,..,4), - концентрации веществ C2H6,C2H4,H2,CH4 соответственно, kx > 0, k2 > 0 - константы скоростей химических реакций. Так как концентрации ct представляют собой неотрицательные величины, то поведение решений системы достаточно рассматривать при c; > 0. Для системы (11) ставится задача определения положения равновесия по заданным начальным концентрациям

С1(0) = cf,c2(0) = c   ,c3(0) = c’0),c4(0) = ' .

Приравнивая правую часть системы (8) к нулю, находим, что положения равновесия образуют множество векторов вида

(0 A

c =

c 2

^C 3

, где ci eR+, i = 2,3,4.

к ^c 4 )

Фиксируя некоторые c ^ 0, (i = 2,3,4) и используя определения локальной покомпонентной асимптотической эквивалентности, исследуем на устойчивость по части переменных ненулевое положение равновесия c* = colon (0, c2 *, c3 *, c4 *), а также асимптотику решений системы (11) в окрестности этого положения равновесия.

Для этого в системе (11) сделаем замену переменных c = x + c *.                                              (13)

Тогда система (11) будет иметь вид

x] = — kx — 2 k2x 2 x2 = k j X j + k2x 2 x 3 = k i x i              . x =2kx 2 x^     ^/v^ x]

(14)

Заметим, что вид систем (11) и (14) совпадает. Таким образом, задача сводится к исследованию асимптотики поведения решений в окрестности тривиального решения x = 0 системы (14).

Так как матрица линейного приближения

^ ' A = - ki Ji y 2 = ki У1                                           (15) y 3 = ki У1 . y 4 = 0 системы (14) имеет одно отрицательное и три нулевых собственных значений кратности 1, то нулевое решение системы (15) является устойчивым. Вместе с тем согласно [22] имеет место критический случай, и, следовательно, теорема Ляпунова об устойчивости по первому приближению [1] неприменима.

Исследуем устойчивость по части переменных нулевого положения равновесия системы (14) на основании локальной покомпонентной асимптотической эквивалентности по Брауеру.

Используя определение 3, установим соответствие между начальными значениями

X (0) = x((0), x2 (0) = x(0), x3 (0) = x(0), x4 (0) = x(0)

решений

X j ( t : 0, x ⁽⁰⁾ ) =

kx ⁽ ° ⁾ e ^{— k} 1 t

k + 2 k^x_x -⁰⁾ (1 - e ^{k 1} ‘ ),

x ₂ ( t : 0, x ⁽⁰⁾) = x ⁽⁰⁾

к   (    к

+- k —in 1 + 2 k 2 x га

4 k2  к    k

k

\

4 k

— e - ^k 1 t

V<°) ( ) + xr

(1 - e

— J

^{k 1} t )( k + 2 k₂x ( ⁰⁾ ) '

_k k , + 2 k,x ,^;0) (1 — e- ^kt ) ₇ ’

x ₃ ( t : 0, x ⁽⁰⁾ ) = x Г

k

(0Л    г'"1

x ( t : 0, x ) = x —

+- k -in 1 1 + 2 k ² x га

2 k 2 к       k 1   ¹

< k

—

k

2 k

^k 1

e ^— k ¹ t )  ,

In 1 + 2   2 x ⁽⁰⁾ (1 — e - ^{k 1} t )   + x ^:0)

( (1 — e

— J

^{k 1 t} )( k + 2 k₂x_A ⁽⁰⁾ ) '

' 2

к

k ₁

к k + 2 kx ^(l — e - k i t ) J ’

нелинейной системы (14)

и начальными значениями y₁ (0) = у ₃ ⁽⁰⁾ , y₂ (0) = y ⁽⁰⁾ , y₃ (0) = y ( ⁰⁾ ,

У4 (0) = У ( ⁰⁾ решений

У 1 ( t :0, y Г = у Г e ^— k¹

у 2 ( t :0, у ⁽⁰⁾) = у 2 ⁰⁾ + y^k (1 — e ^{— k 1} t ) у ₃( t :0, y ⁽⁰⁾) = y Г + y ^C — e-^{k 1} t ) , y 4 ( t :0, у ⁽⁰⁾) = у 4 ⁰⁾

линейной системы (15).

Для этого определим отображения P ⁽¹⁾ и P ⁽²⁾ из условий

|im ЗЮ—УЮ = 0, i = -, t -       Ц i (t)

где в качестве функций ц,( t ) выбраны следующие:

Ц 1 ⁽ t ) = ^{e — k 1} t , Ц 2 ^{( t} ) = Ц 3 ^{( t} ) = H 4 ^{( t} ) = ^{1 — e — k 1} t

.

Имеем к x(0)

(0) _ d(2)_y(0) ₌     ^k 1 ^x 1

У1    P  x1  _ k, + 2kx(0) , y 20)

_ p (2)_v(0)

— ^p ₂   Л '

- x ⁽⁰⁾

k

+    ¹ ln

4 k₂

1 + 2 ^k x ⁽⁽⁰⁾ k i    ¹

-

A

f k — 2 k₂X j^{(0) л}

_V k + 2 k₂X j ⁽⁰⁾ _y

к ( к У ( к х ⁽⁰⁾

y(0) — P3(2)x(0) - x(0) + k' In 1 + 2 k X((0)

^{3     3   1      3}     2 k₂    V      k ¹  ) V k + 2 kx ⁽⁰⁾

y Г — P ₄ ⁽²⁾ x ⁽⁰⁾ - x ⁽⁰⁾ — k ' In ^f 1 + 2 k x ⁽⁰⁾ 1 + x ⁽⁰⁾ ,

* 4         4      1          4       л j                   7     11

2 kk,

P ²⁾ — colon ( P ²⁾, P ₂⁽²⁾, P ²⁾, P ²⁾) .

Обратное отображение P(1) имеет вид к v(0)

X 1 ⁽⁰⁾

_ p (1) _v(0) ₌     ^k 1 ^y 1

= ¹ y ¹   - k 1 — 2 k 2 y r

X ⁽⁰⁾

— P 2 ⁽¹⁾ y 2 ⁰⁾

,⁽⁰⁾ + -L1J1 — 2 k 2 y :»)

4 к  V k ₎

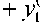
k 2 y '

V ^k 1 ^{— 2} к 2 ^{y (0)}

_r(0) _ p(1)_n,(0) _   (0)      (0)      k_x     ^f kk 2   (0)

^X 3   ^{— P} 3 ^y 3   ^{- y} 3 ^{+ y} 1   ⁺ 7T^{1n 1 — 2} у ^y 1

^{2 k} 2         ^k J

x ⁽⁰⁾

^X 4

— P 4 ⁽¹⁾ y 4 ⁰⁾ - y 4 ⁰⁾ + 2 y ( ⁰⁾

J^ln 1 — 2 ^k y ⁽⁰⁾-- ^{k 1} y ¹   _m,

2 k₂    V      k ¹  ) k — 2 k₂y ( ⁰⁾

P ⁽ '' — colon ( P ⁽ ', р 1) , р ⁽¹⁾, P ( ¹⁾).

Тогда, области V и U могут быть построены следующим образом:

V — V ' x V 3 x V 3 x V 4 , V 1 —

■ от,------

2 k 2 )

V i — ( 0, +» ) , i — 2,4 ,

U — U x U ₃ x U ₃ x U ₄, U —

—

V

к        }

, +от , U — 2 k 2       ) i

k

--1- , +®

2 k₂

i — 2,4 .

Величины 5г (t: t0, x (0)), i —1,4, имеют вид kxl(0) e—k1 t

S ' ( t : t 0 , x ⁽⁰⁾) —

k + 2 k₂x ⁽⁰⁾ (1 — e ^{— k 1} t )’

M t : 1 0 , x ⁽⁰⁾) —

^k 1

4 k 2 (1 — e - ^{k 1} t )

ln

1 + 2 ^ x ^Q — e -^k t ) k 1    ¹

1 + 2 x ^0: k 1   ¹

+

X ^ f (1 — e ^kt )( k + 2 k x :⁰⁾ ) ² + ( k — 2 k x ^:0) )( k + 2 kx ^⁰⁾ (1 — e ^{k 1 t} )) i ⁺ 2 V          (1 — e~^kt )( k + 2 kx ⁽⁰⁾ )( k + 2 kx ⁽⁰⁾ (1 — e ^{— k 1 t} ))          _y

5₃ ( t : t ₀, x ⁽⁰⁾) =-----——— In

^{3     0}            2 k ₂ (1 - e - ^k 1 t )

1 + 2 k x ⁽⁰⁾ (1 - e- ^kt ) k i

1 + 2 ^k x ⁽⁰⁾

k '   ¹

kx ⁽⁰⁾ e ^{- k1}

+-- 777---------------;----;

( k + 2 k₂x ⁽⁰⁾ )(1 - e - ^k' ¹ )

S₄ ( t : t ₀, x ⁽⁰⁾) = ln

^{4     0}             2 k ₂ (1 - e -^{k 1} )

1 + 2 ^ x ⁽⁰⁾ (1 - e - ^k 1 ¹ ) k 1    ¹

1 + 2 ^k x ⁽⁰⁾

k ₁    ¹

I (0)

+ x ( )

⁴ k + 2 k₂x^ 1

₄ k + 2 k₂x ₁ ⁽⁰⁾ (1 - e - ^k1 )   1 - e ~^kt ^

и удовлетворяют условиям (6) теоремы (1).

Заметим, что системы (14) и (15) не удовлетворяют определению асимптотической эквивалентности в смысле работ [11-13], так как области определения отображений P ⁽¹⁾ и P ⁽²⁾ не совпадают со всем пространством Rⁿ , и, следовательно, во всем пространстве R ⁿ не существует отображений, переводящих начальные данные одной системы в начальные данные другой, так чтобы норма разности соответствующих решений стремилась к нулю при t > .г .

Так как P ⁽¹⁾ = P ⁽²⁾ , то системы (14) и (15) локально покомпонентно асимптотически эквивалентны по Левинсону в смысле определения 3.

Учитывая, что отображения P ⁽¹⁾ и P ⁽²⁾ непрерывны в нуле, получаем, что все условия теоремы 1 выполнены.

Так как нулевое решение системы (15) асимптотически устойчиво по первой компоненте, а ненулевые решения имеют асимптотическое равновесие по остальным компонентам, то на основании теоремы 1 можно сделать вывод, что этими же свойствами обладают решения системы (14) в окрестности нулевого положения равновесия.

Учитывая замену переменных (13), можно сделать следующие выводы об асимптотическом поведении решений системы (11) в окрестности положения равновесия c * :

• 1)    каждое положение равновесия c * системы (11) является асимптотически устойчивым по компоненте c ;

• 2)    решения системы (8), начинающиеся в окрестности положения равновесия c * , имеют асимптотическое равновесие по компонентам c ₂, c ₃, с ₄, причем при 1 > +ю эти решения стремятся к нему.

Поведение решений асимптотически эквивалентных систем в окрестности положения равновесия. Так как правые части систем (11) и (14) совпадают, то из асимптотической эквивалентности систем (14) и (15) следует асимптотическая эквивалентность систем (11) и (15). Тогда формулы (19) и (20) остаются справедливыми, если x ⁽⁰⁾ заменить на c ⁽⁰⁾ .

Построим графики решений для локально покомпонентно асимптотически эквивалентных по Левинсону систем (11) и (15) относительно некоторых функций (18), с начальными данными, связанными отображениями P ⁽¹⁾ и P ⁽²⁾ согласно формулам (16) и (17), где x ⁽⁰⁾ заменены на c ⁽⁰⁾ . В качестве начальных значений решений выбраны c ( ⁰⁾ = 1, c⁰ ) = C 0 = c (0) = 0 и y ⁽⁰⁾ * 0.78, y ( ⁰⁾ « 0.16 , r ( ⁰⁾ ~ 0.1 , y ( ⁰⁾ - 0.12 . Графики построены для k = 0.51, k₂ = 0.07 , что соответствует протеканию брутто-реакции пиролиза этана при постоянной температуре 800 K .

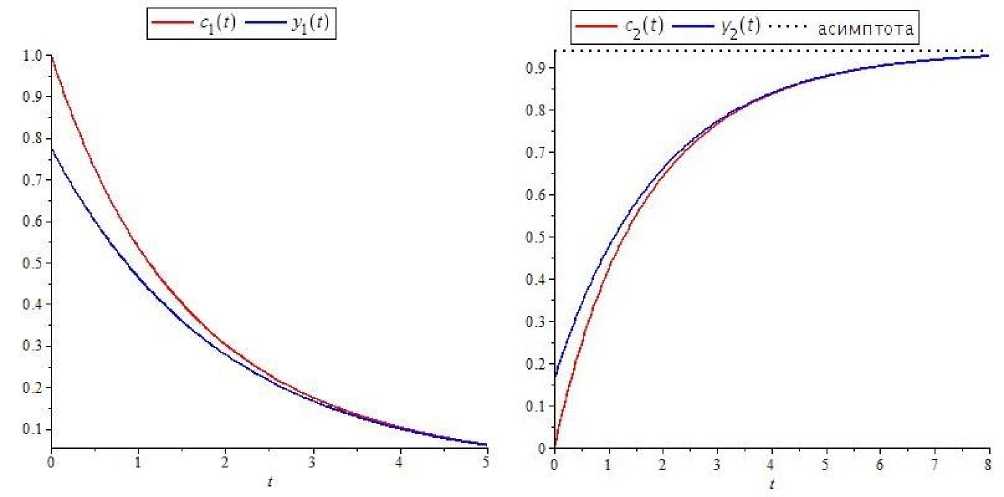
Рис. 1. Графики решений с; и x,, i = 1,2, между начальными значениями которых установлено взаимно-однозначное соответствие.

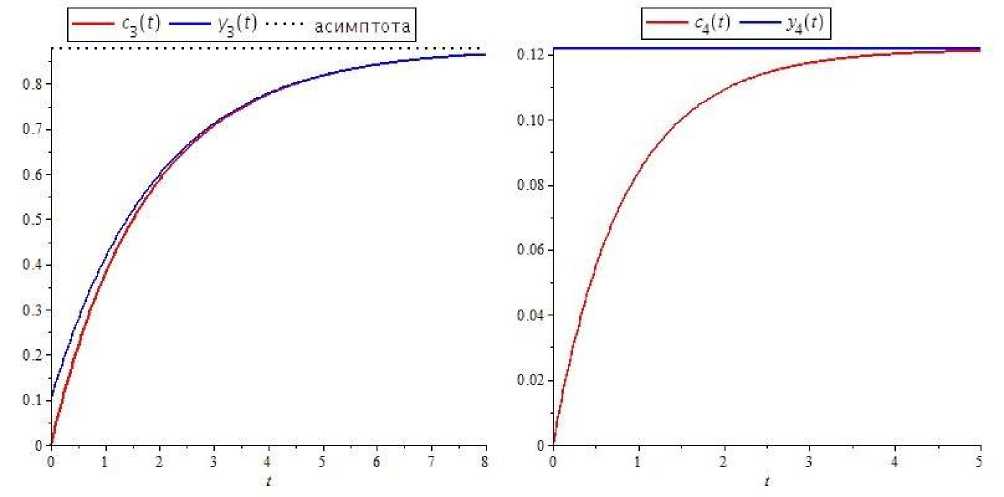
Рис. 2. Графики решений с; и xt, i = 3,4, между начальными значениями которых установлено взаимно-однозначное соответствие.

Положения равновесия для решений с вышеприведенными начальными значениями систем (11) и (15) совпадают и находятся по формулам lim c (t: 0, x(0)) = lim y{ (t: 0, y(0)) = 0, t→∞ limc2 (t: 0, x(0)) = limy2 (t: 0, y(0)) « 0.94, t→∞ limc3 (t: 0, x(0)) = limy (t: 0, y(0)) » 0.88, t→∞ limc4 (t: 0, x(0)) = limy4 (t: 0, y(0)) « 0.12. t→∞

Заключение. Таким образом, на основании локальной покомпонентной асимптотической эквивалентности для системы (11) определено положение асимптотического равновесия по заданным начальным концентрациям и исследована асимптотика поведения решений в его окрестности. Из проведенных исследований можно сделать вывод, что исследуемая система обладает свойством полиустойчивости по части переменных [23; 24].