Локальные параметры теплоотдачи на участках развивающегося температурного пограничного слоя в полостях газовых турбин

Повышение термических характеристик, проектируемых узлов и агрегатов ТНА напрямую зависит от проведения исследований на предмет локализации температурного воздействия газовых потоков. С целью повышения точности и совершенствования расчетных методик необходимо более точно определять численные значения характерных величин газового потока, влияющих как на потери в элементах проточного тракта, так и на энергетические и рабочие параметры турбин [1].

Одним из методологических подходов к решению задачи проектирования элементов газово-дов и моделирования энергетических параметров является аналитический вывод зависимостей путем преобразований уравнений динамики [2].

Рассмотрим вывод уравнений законов теплообмена и локальных коэффициентов теплоотдачи с использованием аффинноподобной модели температурного пограничного слоя для случая Pr < 1 [3].

u

U

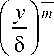
При Pr = 1 профиль распределения скорости в динамическом пограничном слое должен иметь производную на стенке, т. е. удовлетворять условию, требуемому дифференциальным уравнениям движения пограничного слоя. Поэтому будем использовать двухслойную модель распространения профиля скорости с ламинарным подслоем и турбулентным профилем в основной части.

Условия, требуемые дифференциальными уравнениями движения пограничного слоя, должны выполняться и для дифференциального уравнения энергии [4–7]. В работе аппроксимируется профиль скорости в пограничном слое кубической параболой:

u _ 31 У | 11 У U ~2(sj-2Us

Кубическую параболу используют также для аппроксимации температурного пограничного слоя:

T - T o = 3 ( y_ ) 1 y_ T s - T o 2 (5 1 J 2 (5 ₁ J

Отношение толщины температурного и динамического пограничных слоев в произвольном сечении обозначим как у В. М. Кейса:

r = —- или 5, = r -5 . 5 ^t

Отметим, что использование уравнения кубической параболы возможно только для ламинарного пограничного слоя. Принимается, что распространение профиля скорости и распределение профиля температур в пограничном слое аппроксимируется следующими полиномами:

u = (2n-2n3 +n4), T^T0- = (1 -2Пt + 2n3-n4).

^U                        T 5 T O

В соответствии с работой В. М. Кейса, используем отношение температурного пограничного

Рис. 1. Профили распределения температурного и динамического пограничных слоев при Pr < 1

Профили распределения пограничных слоев показаны на рис. 1.

Разобьём границы уравнения (8) на два самостоятельных участка интегрирования:

Fig. 1. Distribution profiles of temperature and dynamic boundary layers for Pr < 1

– от соприкосновения потока с поверхностью тока до толщины динамического пограничного слоя 8 ;

- от окончания толщины динамического пограничного слоя 8 до окончания толщины температурного пограничного слоя 8 t .

Отсюда уравнение (8) преобразуется к виду

**

8 U

8; ; =j- 1

Т - Т 0

⁸ 1 u

Т - Т о

0 U V

Т 8

Т о )

Т 8

Т о )

dy .

Выражение для толщины потери энергии при известных профилях аппроксимации пограничных слоев принимает следующий вид:

** ⁸( y ) m

⁸ 1 Ф = JI s I

о\8 )

1 -

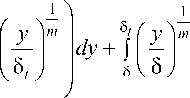
V

-

1 A

dy .

Произведём замену переменных:

A = lf y 1 m о V ⁸ ?

1 -

y 1 m sTI

,         8‘ ( y A m dy, B= J HI

8 V ⁸ ?

1 -

y 1 m

dy .

В первом члене введем замену через отношение толщины температурного и динамического

8Z пограничных слоев в произвольных сечениях r = — , тогда

1 A 1

A = J

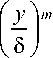
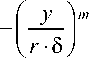
8 _;m dy = J y r •

8 ^m

(

8 _1;m

J y r

⁰ Vs ^m

y^m 21

8 m • _r ^m

dy =

m • y • y^m

8 ^m ( m + 1 ) 8

m • y • ym m • rm • (m + 2)

/1

m •S^ m • r^m + 2 • r^m - m - 1

8^ m 8^ m _ V>

(m +1)   1— rm • (m + 2)        rm • (m +1) • (m + 2)

где r – отношение толщины температурного и динамического пограничных слоев.

Границы интегрирования второго члена уравнения (10) находятся от толщины динамическо го пограничного слоя 8 до толщины температурного пограничного слоя 8t. При этом измене- ния эпюры скорости вдоль оси Y не происходит, а скорость равна скорости потока в ядре тече- ния. В этом случае

u

U

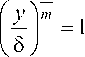
Тогда

B =J 1

m • y • y^m

8 t ^m ( m + 1 ) ₈

m • 8 m + 8 m

111    1

+

m - 8 t m + 1

5-5 m -5 t -5 m -5-5 m - m + 8 m 8 m

5 tm (m +1)

С учетом выражения (12), толщина потерь энергии температурного пограничного слоя оп- ределится как

m-5- m- rm + 2• rm -m -1

5t v = A + B =

rm - (m +1)(m + 2)

111    1

5-5 m -5t -5 m -5-5 m - m + 5 m 5 m

5 tm (m +1)

Учитывая отношение толщины температурного и динамического пограничных слоев в произвольном сечении, второй член уравнения толщины потери энергии (12) преобразуется к виду

B = -

5(5r)m +5m(5r)m -5r(5r)m -5-5mm

(m +1) (5 r) m

Отметим, что при r = 0, что характерно для Pr = 1, первый член уравнения (13) запишется как A = 5 ** , а второй член уравнения обнуляется, т. е. B = 0 .

Учитывая выражение (14), перепишем выражение для толщины потери энергии (13):

m 5 mr m + 2 r^m - m - 1

** V 2

⁵ 1 ф

rm (m +1) - (m + 2)

5 ( 5 r ) m + 5 m ( 5 r ) m -55 _m

( m + 1 )( 5 r ) m

f 11  )

m 5 mr m + 2 r^m - m - 1

5 m - mr m + rr^m

1))

- r^m

m

2 r - m +—_r

+ mr -

v

rm

rm (m +1) - (m + 2)

^m ( m + 1 )

( m + 1)( m + 2)

.

Запишем уравнение закона теплоотдачи в виде критерия Стантона:

X-

p-Cp - U-(T5-To )

p-Cp -U-(T5-To)

X p- C p • U

d dy

-

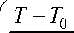
Для дальнейших вычислений найдем производную температурного пограничного слоя на стенке. Используем двухслойную модель турбулентности с ламинарным подслоем при коэффициенте Прандтля Pr = 1. Тогда толщина температурного пограничного слоя и динамического пограничного слоя будут равны, т. е. 5 = 5 t [8; 9].

В данном случае при Pr < 1 приняли 5 t = r 5 . Проведя аналогию между температурным и динамическим пограничными слоями с учетом коэффициента отношения толщины и выполнив соответствующие преобразования, получим производную температурного пограничного слоя на стенке:

Afт - т0)

^d y V T 5 - T o j y = 0

U

«л-v

X^-v ) ^{m + 1}

1б t • U j

U

«л-v

а л - v A m+1 r-5-U 2 .

Из уравнения (15) выразим толщину динамического пограничного слоя:

8=  8V(m +1)(m + 2)

.

m

2 r - m + — + mr - 2

rm

Полученное выражение для толщины динамического пограничного слоя (18) подставим в выражение производной температурного пограничного слоя на стенке (поверхности теплообмена) (17):

a

T - T o

dy ( T5- To

I = ^U

I y = o ^а Л "^V

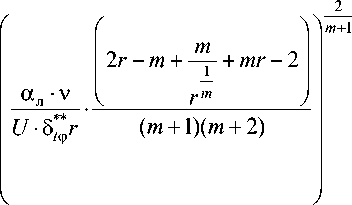
m + 1

или

2 r

m

m +—+ mr - 2

a

rp rp \          ^{m 1}

T T o I = U m + 1 .

m

dУ ( T5- To

y = o

m - 1 a m ^{- 1} -V r

•

( m + 1)( m + 2)

^X 2 \    7

X i m + 1 ^u t v )

.

Определив производную температурного пограничного слоя на стенке (поверхности теплообмена) (20), а также закон теплообмена в виде критерия Стантона (16), получим

(f                           m + 1

m

2 r - m +—- + mr - 2

m

St =

X p-Cp .Um+1

( m + 1)( m + 2)

•

.

a m - ‘ .V ²

Для использования уравнения (21) в проектных расчетах требуется определить коэффициент ламинарного подслоя α л , который, исходя из двухслойной модели турбулентности, определяем из условия смыкания ламинарного подслоя и турбулентного профиля [10–11]. Определяем коэффициент ламинарного подслоя α л аналогично, как и при Pr = 1, с использованием закона трения и производной на поверхности теплообмена для функции распределения температурного пограничного слоя [12]. Исходя из выражения для толщины потери энергии температурного пограничного слоя (15), запишем

m

2 r - m +—+ mr - 2

m + 1

rm

0,25

2 ( m - 1 ) m + 1

(m +1)( m + 2)

« л

2 ( m - 1 ) m + 1

m

2 r - m +—- + mr - 2

rm

(m +1) (m + 2)

m + 1

•

m < 5

(m +1)( m + 2)

0,25

.

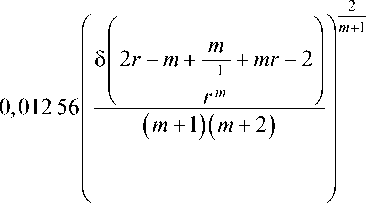
При m = 7 выражение (22) преобразуется к виду 12,5496 ^а л = r 0,167 ^.

5 1                           -

Учитывая, что при Pr < 1 r = — = —-, получим а _л = 12,5496Pr ¹⁸ .

Pr ³

С использованием выражения (21) запишем интегральное соотношение уравнения энергии температурного пространственного пограничного слоя:

• ¹    5 ** J 5 **        ^{1 д Н} ф ** J ^{д Н} _ф **

77 ~"51 ф +77-   (85 t ф )+ 77—7—"51 ф + "7г—7—"851 ф =Нф дФ     HVN      Нф" Нф дФ     Нф" Нф дф m+1

m

2r - m +—- + mr - 2

m

X

Р" C p • U m + 1

( m + 1)( m + 2)

a m-1 "V 2

S i m + 1

^u 1 ф )

^Фс^^+^^Ь

Р" C p ( T b - T o ) .

Рассмотрим случай реализации вращательного течения, когда направление потока определяется кольцевой линией [13]. Выразим уравнение энергии (23) в цилиндрических координатах, учитывая, что для осесимметричного течения при 8 = const выполняются соотношения:

d H_(D  dR             d H,     а

Ф = а , ф = R , --Ф = — = 1, Нш = 1, —ф = 0, — = 0: дф  dR      ф дф дф m+1

m

• 2    r - m +—. + mr - 2

  m

  
  

  ^д ** J "⁸ **

  J "8---0.. +---0, . =

  д R  ^{1 Ф} R    ^{1 Ф}

  
  

  ( m + 1)( m + 2)

  
  

  a m ^{- 1} "V ²

  
  

  ^X 2

  
  

  _-

  
  

  ^тфо ( 1 ^{+ 8} 2 )

  
  

  Р" C p •( T ₅- T o )‘

  
  
  
  

• 2.    Локальная теплоотдача турбулентного потока при вращательном течении

С использованием аффинноподобной модели температурного пограничного слоя, определение вида закона теплообмена становится тривиальной задачей. Использование уравнения (24) происходит после интегрирования с учетом принятых законов распределения.

Представим течение в турбине ТНА и соответствующее ему вращательное движение по закону твердого тела. Пренебрегаем диссипативным членом в интегральном соотношении уравнения энергии (24) при реализации вращательного течения:

5 ** J -e **

J " eo,„ +o,„ — dR tф    R tф m+1

m

2 r - m +—— + mr - 2

m

X p-Cp • Um1

( m + 1)( m + 2)

a m ^{- 1} -v ²

S I m + 1 ^u t ф )

.

Для вращательного течения по закону «твердого тела» распределение окружной составляю- щей скорости по радиусу

U

— — to — const

R

[14], уравнение (25) преобразуется следующим образом:

m + 1

m

2 r - m +— + mr - 2

m

**

^d o ** . ⁰ 1 ф d R t ^ф    R

X

J - e - p - Cp • tom+1

x

( m + 1)( m + 2)

a m ¹ -v ²

•

R m + 1 ( s ** ) m 2

.

Введем промежуточные обозначения:

A —

X

J - e - p - Cp - tom+1

**

⁰ t ф

= y ,

m + 1

m

2 r - m +—r + mr

m

( m + 1)( m + 2)

a m ^{- 1} -v ²

,

тогда

dy + 2 -dR R

^_A ^ — 0.

R m + 1 _- y m + 1

Уравнение решается методом подстановки y = и • v :

du dv

v

--v + и + и — =

dR dR

R

A

22  2 ,

U m + 1 • v m + 1 • R m + 1

f dv v )     du A

.

U ++

( dR R J    dR    2^ 2^ 2l_

U m + 1 • v m + 1 • R m + 1

dv v

Функция v должна удовлетворять условию--1— = 0 , тогда v = — , откуда находим dR RR m+3 A• R2 •(m + 3)

U = m+1 —  —-

1 m + 3 A • R ² • ( m + 3 )   m + 3 A • R ² • ( m +

= — m+1 --------------^- = m+1 --------i---- tФ R ^ 2 •( m +1)        ^ 2 •( m +1)

**

,

m + 1

m

2 r - m +—r + mr - 2

m

**

0 t ф =

m + 3

m + 1

X

2 ^Х

J • е • р • Cp - tom+1

( m + 1)( m + 2)

a m - 1 -v ²

2 •( m +1)

•( m + 3)

• R

Выведем критерий Стантона для вращательного течения по закону твердого тела для турбулентного режима с учетом выражений (21) и (30).

f     И C p

Задав Pr =---- ^X

и I Re = ^Р^^Ф | , выразим критерия Стантона для вращательного течения

I И J по закону твердого тела для случая Pr < 1:

f

m + 3

St =----- m + 1 m + 3

Pr

2 J E

m

2 r - m +—1—+ mr - 2

m

r

a r (m+2)( m+3)Re л                                 to

.

Рассмотри течение газового потока в магистралях подвода ТНА, которое осуществляется по закону свободного вихря ( U • R = C = const ) [15], тогда уравнение энергии (25) запишется как

**      **

^{d 0} 1 Ф + ⁰ 1 ф dR   R

X

2 ^Х

J -е-р- C p • C m + 1

x

Проведем замену:

m

2 r - m +—- + mr - 2

m

( m + 1)( m + 2)

m - 1 ^а л

• v

m - 1

m + 1

R m + 1

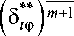
51Ф = У,

B =

X

J-s-p-Cp • Cm+1

a

m

2 r - m +—p + mr - 2

к_________ rm_________>

( m + 1)( m + 2)

m - 1

а m-1 •v ~ • r

A m + 1

Решение уравнения (27) ведем аналогично случаю вращательного течения по закону твердого тела при Pr < 1 методом подстановки y = и • v, причем m+1

v = R ,

U =

Bm+3 • RR m+1

2 m + 3

Тогда толщина потери энергии определится в виде

**

⁵ 1 Ф

m + 1

B A m + 3

J

• R .

С учетом полученного ранее выражения В запишем:

**

51 ф =

X

2 J •s^ C p • C m +

m

2 r - m +—- + mr

m

( m + 1)( m + 2)

a m ^{- 1} •v ²

m + 1

/2

m + 1

m + 3

• R .

Тогда критерий Стантона для вращательного течения по закону свободного вихря для случая Pr < 1 определится, как

2 J E

m

2 r - m +   + mr - 2

St =

m + 1

Pr m + 3

m

a m "1 r ( m + 1)( m + 2)Re _m

m + 3

.

Таким образом, выражены все переменные для определения локальных коэффициентов теплоотдачи в виде критерия Стантона при различных законах течения по аффинноподобной модели температурного пограничного слоя [16].

На рис. 2 представлены значения безразмерного коэффициента теплоотдачи в виде критерия Нуссельта для турбулентного вращательного течения по закону «твердого тела» [17; 18].

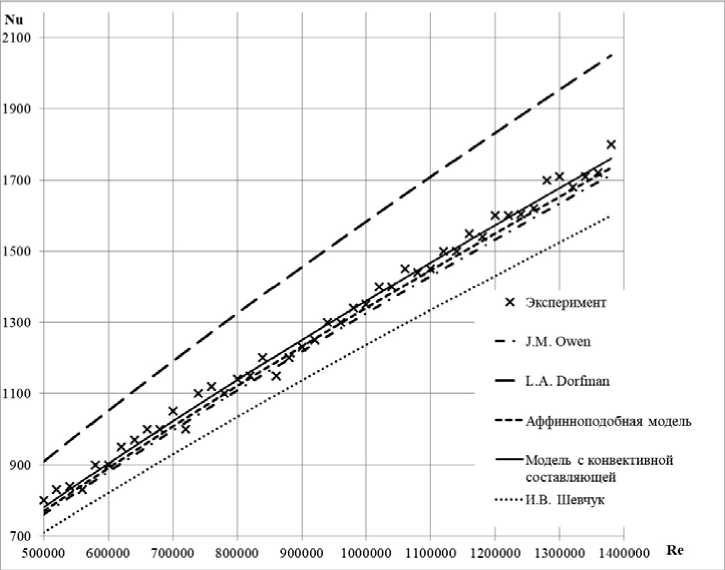
Рис. 2. Коэффициента теплоотдачи при Pr = 0,7

Fig. 2. Heat transfer coefficient at Pr = 0.7

Заключение

Для сопоставления полученных в исследовании результатов с работами других авторов, используем данные эксперимента для случая турбулентного вращательного движения воздуха по закону «твердого тела» с диапазоном изменения критерия Рейнольдса Re = 5 • 10⁵ - 1,4 - 10 6 , критерия Прандтля Pr = 0,7 [17]. При сравнении со значениями модели с конвективной составляющей аффинноподобная модель показывает схождение результатов на уровне 1,5 %.

Теоретические зависимости, полученные по моделям распределения температурного и динамического пограничных слоев с конвективной составляющей и аффинноподобными профилями при Pr = 0,7, дают достаточно близкие результаты в связи с близким подобием распределения температурного и динамического слоев и близки к случаю Pr = 1.

Полученные результаты исследования и их соотношение с результатами других авторов показали, что они пригодны для инженерных расчетов и анализа воздействия локальных коэффи- циентов теплоотдачи на высокотемпературные узлы ТНА. Необходимо отметить, что на безразмерный коэффициент теплоотдачи в виде критерия Нуссельта существенно влияют граничные условия течения и теплообмена, такие как скорость, вязкость, плотность и градиент температур рабочего тела и поверхности теплообмена.