Локальные повреждения в эндопротезе тазобедренного сустава из углерод-углеродного композиционного материала при перегрузках

ВЕСТНИК ПНИПУ. МЕХАНИКА № 6, 2023PNRPU MECHANICS BULLETIN

Углерод-углеродные композиционные материалы (УУКМ) с пиролитической углеродной (ПУ) матрицей – это класс конструкционных материалов, который благодаря своим уникальным свойствам нашел широкое применение в машиностроении, металлургии, химической промышленности и многих других отраслях.

Такие свойства УУКМ, как биогенность (свойство контактировать с живыми тканями, не вызывая отторжения) [1], высокая поверхностная энергия, которая позволяет адсорбировать и удерживать на своей поверхности биологически активные соединения и живые клетки и инертность, возможность резорбироваться (разрушаться) без образования опасных, токсичных продуктов, позволяют использовать его в медицинских целях в качестве имплантов для человека и животных [2-4]. Уникальность УУКМ еще и в том, что за счет сочетания свойств низкомодульного углеродного волокна и ПУ-матрицы имплант имеет схожие упругие характеристики к нативной кости человека, что исключает возможную резорбцию костной ткани.

Одним из наиболее востребованных направлений для применения УУКМ является эндопротезирование тазобедренного сустава (ТБС). Ежегодно в мире осуществляется около 2 млн имплантаций ТБС [5; 6]. По последним данным в Российской Федерации за 2018 год было выполнено 70 316 операций по эндопротезированию ТБС [7], а ревизионных операций – 16,6 % от первичных операций [8]. Так как ТБС человека является наиболее нагруженным суставом, то эндопротез ТБС должен обладать высокими прочностными характеристиками. Например, при передвижении человека в обычном темпе по ровной поверхности нагрузка на сустав достигает двух значений веса тела за вычетом веса опорной ноги (P), а при подъеме и спуcке – 2,5 P. Это соответствует нормальной эксплуатации эндопротеза. При этих нагрузках не должно происходить разрушений конструкции. В отдельных случаях возможны повышенные нагрузки – случайные толчки, удары при потере равновесия и т.д. При перегрузках возможны локальные повреждения. Прогнозирование таких локальных событий важно для анализа работоспособности конструкций из композитов. Исследованию прочностных характеристик эндопротезов посвящено множество работ [9–17].

В работе [17] определена актуальность разработки эндопротеза ТБС из УУКМ, разработана инженерная компьютерная модель деформирования эндопротеза, позволившая оценить его несущую способность, определены слабые места в углеродной части конструкции, выявлено, что разрушение наступает от сдвиговых напряжений вдоль углеродных волокон без разрушения самих волокон. УУКМ в этой части протеза является однонаправленным композитом. Поэтому наиболее слабый компонент во всех типах УУКМ – углеродная матрица, в данном случае пироуглеродная, – играет решающую роль в инициации повреждений эндопротеза. Упомянутая компьютерная модель эндопротеза является детерминированной. Свойства всех материалов принимались фиксированными, повреждение материалов следовало детерминированным критериям. В частности, считалось, что УУКМ есть однородный материал с фиксированными эффективными свойствами. Согласно этой модели углеродная часть определяет несущую способность эндопротеза. Запас прочности составил около 1,15.

Однако УУКМ отличаются от других композитов значительно большим разбросом свойств. В значительной степени это обусловлено неоднородной стохастической структурой матрицы. Углеродная матрица с точки зрения мезомеханики есть поликристалл, состоящий из сильно анизотропных зерен пироуглерода. Процессы деформирования в ней стохастичны и существенно нелинейны. В данной работе учитывается реальная микроструктура материала и ПУ-матрицы, приняты во внимание процессы разрушения матрицы, которые протекают в несколько стадий с постепенной деградацией упругих свойств, ее повреждаемость, которые могут возникать при перегрузках. Пиролитическая углеродная матрица образуется при термическом разложении углеводородов и дальнейшем осаждении продуктов разложения на некаталитической поверхности [18–20]. ПУ обладает стохастической структурой по причине того, что количество и расположение активных центров, с которыми взаимодействуют молекулы углеводородных газов, и радикалы являются случайными величинами. Случайными величинами, соответственно, являются и форма, и размеры, и ориентация кристаллографических осей зерен пироуглерода. Таким образом, поля напряжений и деформаций на мезоуровне являются стохастическими, а на макромасштабном уровне есть величины детерминированные. ПУ матрица содержит множество дефектов (трещины, поры). Соответственно, повреждения ПУ-матрицы, количество дефектов существенным образом влияют на упругие и прочностные характеристики изделия из УУКМ. Также у матрицы есть одна особенность, которая не позволяет определить свойства экспериментально. Невозможность экспериментального определения механических свойств связана с тем, что ПУ-матрица не существует отдельно от подложки (волокнистого каркаса), ее свойства необходимо моделировать.

1.    Моделирование повреждений ПУ-матрицы в композите

Эксперименты по нагружению эндопротеза в лабораторных условиях выявили, что начальное разрушение углеродного материала происходит в шейной части от сдвигов вдоль волокон при нагрузке около 1900 Н. При этом волокна не разрываются, а все разрушения сосредоточены в матрице. Инженерный анализ, выполненный в работе [17] на основе рассмотрения композита как однородного материала с эффективными свойствами, показал, что протез выдерживает рекомендованную ортопедами расчетную нагрузку 1850 Н. Однако уже со времени первых применений промышленных углеродуглеродных композитов было экспериментально установлено, что эти материалы проявляют нелинейное псев-допластическое поведение при деформировании, несмотря на то, что их структурные компоненты (волокна и зерна пироуглерода) являются упругохрупкими. Это связано с протеканием сложных процессов повреждений в материале на разных масштабных уровнях, обусловленных структурными неоднородностями, прежде всего в углеродной матрице. В случае эндопротеза поведение матрицы является определяющим фактором, влияющим на работоспособность протеза.

Матрица состоит из сильно анизотропных зерен пироуглерода со случайной ориентацией их кристаллографических осей. На макроскопическом уровне это однородная среда, но на мезоуровне она существенно неоднородна и имеет стохастическую структуру. Под мезоуровнем для пироуглеродной матрицы понимается масштабный уровень отдельных зерен пироуглерода. Вследствие этого поля деформаций и напряжений (мезополя) в зернах являются сильно флуктуирующими. В отдельных зернах напряжения могут превысить соответствующие пределы прочности, даже при невысоких макронапряжениях. Такие зерна испытывают повреждения, а их свойства изменятся (редуцируются). Это приводит к перераспределению напряжений в соседних зернах, возможно, к повреждению других зерен, изменению свойств матрицы в зоне повреждений и в конечном счете ведет к нелинейному деформированию матрицы и композита в целом. Для описания поведения матрицы в материале эндопротеза и влияния на несущую способность применим модель, описанную в [21].

Матрица является пористой (10 %). Поры рассматриваются как зерна с нулевыми упругими свойствами [21].

Зерно пироуглерода имеет гексагональную упругую симметрию. Тензор модулей упругости в кристаллографической системе координат имеет пять независимых компонент и в матричном представлении (нотации Фойгта) имеет вид

	(с c 11 c 12	c 12 c 11	c 13 c 13	0 0	0 0	0 0
с (0) mn =	c 13	c 13	c 33	0	0	0	.           (1)
	0	0	0	c 44	0	0
	0	0	0	0	c 44	0
	ч 0	0	0	0	0	c 66 у

В (1) ось координат Х 3 направлена вдоль оси гексагональной симметрии.

В инженерных целях для анализа разрушений зерен применим простейший критерий максимальных нормальных и сдвиговых напряжений, содержащий соответствующие пределы прочности. К тому же фактически других прочностных данных для пироуглерода нет. В произвольном напряженном состоянии с j зерно может повредиться по одному из следующих критериев

С33 — С3 ,(2)

7С13 + С23 — Т13 ,

(сп + с22)/2 + 7(сп -С22)2 /4 + с22 > с+ ,

7(С„ -С22>2 /4 + С22 > Т12 , где с+ и с, обозначают пределы прочности при растя жении вдоль осей x3 и x 1, т13 и т12 - пределы прочности при сдвиге в плоскостях x1–x3 и x1–x2 соответственно.

После повреждения по любому из критериев (2)–(5) зерно теряет механическое сопротивление по такому критерию, но сохраняет сопротивление по другим критериям. После разрушения по критериям (2) и (3) зерно не сопротивляется растяжению вдоль оси x 3 и сдвигу в плоскостях x 1 – x 3 и x 2 – x 3 , но продолжает сопротивляться растяжению в любом направлении в плоскости x 1 – x 2 и сдвигу в этой плоскости. Поэтому в любом деформированном состоянии такого поврежденного зерна (которое будем помечать верхним индексом ⁽¹⁾) значения компонент тензора напряжений должны удовлетворять условиям С 3 <  0 и с (3) = 0, с 2₃ = 0 . Этим условиям можно удовлетворить, если редуцировать компоненты тензора модулей упругости соответствующим образом. Например, для деформированного состояния (1) (1) (1) (1) (1)

о ,1 >  о, 8 22 >  о, 8 33 >  о и 8 13 ' о, 8 23 ' о (нет сжатий в направлениях вдоль осей кристаллографической системы координат) нужно положить

' c11   c12   о о о о л С12  си  о о о о о о о о о о (2 ° (1)+ = ,            (6) mn о о о о о о о о о о о о 0 0 000c 66 где верхний значок плюс «+» указывает на растяжения.

Для деформированного состояния     8 (11) <  о,

S(1) << А    С(1) с'' А   ТЛ  С(1) А    С(1) А ^ТЛАТ ИЯ АТС! *Л2*АТГТЛТЛИ

22 <• о,   833  <* о,  и  8,3 '" о,   823  '" о (нет растя.^же.н.и.йв направлениях вдоль осей кристаллографической си- стемы координат) нужно положить

/~' о (1) - ^Cijmn

c11   c12   c13   О   ОО c12   c11   c13   о   оо c13   c13   c 33   о  оо о   о   о   о  оо о   о   о   о  оо

V о    о    о   о  о   с 66 J

Анализ деформированных состояний с комбинацией растяжений и сжатий показал, что вследствие сильной анизотропии зерен пироуглерода такие состояния маловероятны и ими можно пренебречь [21].

В итоге тензор модулей упругости зерна, с учетом возможных повреждений по критериям (2)–(3), во всех состояниях может быть представлен в кристаллографической системе координат в квазилинейном виде, зависящем только от компоненты деформации 8 ₃₃

c m = c H ( 8 33 ) + C m ) ^- [1 - H ( 8 33 )], (8)

где H ( 8 ₃₃ ) есть функция Хэвисайда, равная 1, когда 8 ₃₃ >  о, и нулю в остальных случаях, а тензоры Cm⁺ , Com)^- определяются уравнениями (6) и (7).

Аналогичное рассмотрение повреждений по критериям (4)–(5) ведет к следующему выражению для тензора модулей упругости зерен, поврежденных по этим критериям, j = Co®*H (832)) + j- [1 - H (833))],     (9)

в котором матрицы C i'',2/' и С ^т1 определяются форму-
лами
	( о о о о о о ^
	о о о о о о
С ° (2) + =	о о   с 33    о о о
ijmn	о о о    с 44   о о	,
	о о о о    с 44   о
	V о о о о о о ?
	c d c d c 13   000	)
	cd    c d   с 13     о о о
С ° (2) - = C ijmn	c 13 c 13 c 33   000 000 c 44 00	.        (1о)
	о о о о    с 44   о
V	000000	?

Зерна, поврежденные по критериям (2)–(3), могут быть по мере нагружения повреждены по критериям (4)–(5). Такие зерна полностью теряют механическое сопротивление, за исключением всестороннего (гидростатического сжатия). Но состояние гидростатического сжатия крайне маловероятно, и им пренебрегают. Аналогично зерна, поврежденные по (4)–(5), могут быть также повреждены по критериям (2)–(3) и потерять сопротивление. Полностью разрушенные зерна в данной модели отождествляются с порами. Всего в матрице могут присутствовать четыре типа зерен: исходные неповрежденные, частично поврежденные по критериям (2)–(3), частично поврежденные по (4)–(5) и полностью разрушенные (эквивалентны порам).

Тензор модулей упругости матрицы в целом можно представить в виде суммы тензоров модулей по всем зернам, помноженным на индикаторные функции Xk (r) каждого типа зерен. Эти функции, как функции координат, равны 1 внутри зерен данного типа и нулю в других случаях. С учетом этого тензор модулей упругости матрицы, когда матрица содержит все типы зерен (имеющих механическое сопротивление), в лабораторной системе координат принимает вид

C ijmn ( r) = E X k ( r)C pq^k_r)_% ( r) a jq ( r) a m_r ( r)a_m ( r) , (11) k = 0

где X _k ( r) индикатор кристаллита k -типа, равный единице внутри этого кристаллита, а в противном случае равный нулю. C^o_pq ^{( k} _rs ⁾ определяются с помощью (1), (8), (9) и a _ip ( r) являются направляющими косинусами локальных кристаллографических координатных осей кристаллита в точке r относительно глобальной системы координат.

Напряжения в любой точке матрицы находятся по закону Гука

^ j ( r) = C ijmn ( r^ mn ( r).               (12)

В (12) все величины являются случайными.

Соотношения (11), (12) играют роль квазинелиней-ных определяющих соотношений для пироуглеродной матрицы с упругохрупкими разрушениями зерен.

Нахождение деформаций ε ( m ^ξ n ) и напряжений σ i ( j ^ξ ) является стохастической краевой задачей. Для нетекстурированных поликристаллических сред она решается методом интегральных уравнений для деформаций, изложенным в работах [22; 23]. Нужным для целей этой работы результатом решения являются плотности распределения вероятностей для мезонапряжений в зернах поликри-сталлической среды. Решение находится численно с помощью разработанных ранее специализированных алгоритмов [21].

Описание деформирования пироуглеродной матрицы в этом подходе происходит следующим образом. Нагружение осуществляется пошаговым увеличением макродеформации в матрице ε * ik . Для данной задачи макродеформация (для каждого шага нагружения) берется из решения краевой задачи деформирования эндопротеза в пакете ANSYS, как изложено в предыдущей работе авторов [17]. По макродеформациям упомянутый специальный алгоритм вычисляет плотности вероятностей распределения мезонапряжений в зернах: одномерные типа f ( σ 3( ^ξ 3) ), двумерные f ( σ 1(3 ^ξ ) , σ (2 ^ξ 3) ) и так далее. По ним вычисляются вероятности повреждения зерен на каждом шаге нагружения. Например, вероятность повреждений зерен по критерию (3) равна

π ₀₁ = ∫ f ( σ ₃₃) d σ ₃₃ ,               (13)

σ3(ξ3) ≥σ3+ вероятность повреждений зерен по критерию (4) равна

π ₀₂ = ∫ f ( σ ₁₃, σ ₂₃) d σ ₁₃ d σ ₂₃ , σ 123 +σ 223 ≥τ 13

и так далее. По этим вероятностям вычисляются объемные доли поврежденных и остающихся неповрежденными зерен пироуглерода.

Простой комбинаторный анализ дает следующие связи объемных долей всех типов зерен и вероятностей повреждений на каком-либо текущем N -м шаге нагружения и предыдущем ( N –1)-м шаге.

p0 N=p0 N-1(1-π01)(1-π02)(1-π03)(1-π04), p1 N=p1 N-1(1-π13)(1-π14)+

+ p0 |N-1E1 - (1 - П11)(1 - П12)](1 - П13)(1 - П14 ), p2 N=p2 N-1(1-π21)(1-π22)+          (15)

+ p0 IN-1 [1 - (1 - n03 )(1 - П04)](1 - П01)(1 - П02), p3N=1-p0N-p1N-p2

N

где p0 N – объемная доля целых зерен; p1 N и p2 N – по врежденных; p3 N – полностью разрушенных и пор.

Модель деформирования пироуглеродной матрицы с учетом повреждений реализована в виде алгоритмов. На каждом шаге нагружения численно находятся эффективные упругие модули повреждающейся пироуглеродной матрицы. Эти модули используются для вычисления эффективных модулей однонаправленного углерод-углеродного композита. Эффективные модули композита становятся переменными, начиная с некоторого шага нагружения конструкции, когда появляются первые повреждения зерен матрицы. Алгоритм отслеживает деформированные состояния матрицы и композита. Композит рассматривается как однородный материал с эффективными свойствами.

2.    Моделирование деформирования эндопротеза с учетом повреждений композитной части

Деформирование эндопротеза моделируется в программном пакете ANSYS по методике, изложенной в предыдущей работе авторов [17]. Модель биомеханической системы «эндопротез – бедренная кость» изображена на рис. 1. Направление линии действия силы нагружения соответствует ориентации главного вектора системы сил, складывающегося из веса тела человека за вычетом веса опорной ноги и силы, которая определяется мышечными усилиями мышечных групп [24]. Граничные условия, упругие свойства костных тканей (кортикальной и губчатой) и других неуглеродных материалов приняты такими же, как в [17].

Эффективная гомогенизированная среда композита (УУКМ с ПУ-матрицей) является трансверсально- изотропной. Тензор модулей упругости имеет 5 независимых компонент. Ось трансверсальной симметрии направлена параллельно продольной оси волокна.

Рис.1. Расчетная модель биомеханической системы «эндопротез – бедренная кость»

Fig.1. Engineering computational model of the biomechanical “endoprosthesis – femur system”

Плоскостью изотропии в локальной система координат (ЛСК) в расчетной модели является плоскость YZ . Ось симметрии (ось Х в ЛСК) направлена параллельно продольной оси волокна. В местах, где волокна расположены по некоторому радиусу, ось Х направлена по касательной к продольной оси волокна (рис. 2).

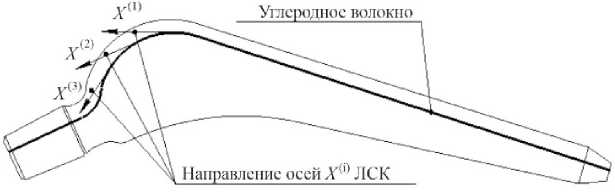
Рис. 2. Направление оси Х ⁽ⁱ⁾ ЛСК

Fig. 2. Direction of axis Х ⁽ⁱ⁾ in local coordination system

В исходном состоянии, перед нагружением, материал эндопротеза имеет однородные эффективные свойства по всему объему. Во время нагружения, которое происходит ступенчато (от 0 до момента разрушения с шагом 0,05 мм) эффективные свойства УУКМ непрерывно меняются (становятся переменными) по причине повреждений зерен ПУ-матрицы. Нагружение осуществляется заданием перемещения суставной головки u.

При нагружении непрерывно перевычисляются эффективные свойства УУКМ, которые являются входными данными модели. При вычислении эффективных упругих характеристик композита используется поли-дисперсная модель среды с цилиндрическими включениями [25; 26]. Свойства углеродных волокон достаточно хорошо изучены [27–30], и в модели их свойства считаются детерминированными. В то же время некоторые упругие модули волокон (например модули сдвига) трудно измерить экспериментально, и они остаются в значительной степени неопределенными. Свойства матрицы генерируются описанной выше моделью, которая использует ряд упрощающих допущений. Все это обусловило использование простой модели для вычисления эффективных свойств композита.

На каждом шаге нагружения осуществляется обмен данными между ANSYS (свойства композита) и алгоритмом из раздела 2, модифицирующим свойства ПУ-матрицы, для перерасчета упругих модулей УУКМ следующим образом:

• –    вычисляются поля макродеформаций и макронапряжений по всему объему эндопротеза методом конечных элементов (МКЭ);

• –    вычисляются плотности вероятностей распределения мезонапряжений в зернах ПУ и вероятности повреждения зерен на каждом шаге;

• –    вычисляются объемные доли всех типов зерен;

• –    вычисляются эффективные свойства поврежденной матрицы;

• –    эффективные свойства материала углеродной части эндопротеза пересчитываются, и решается краевая задача для всего протеза.

Переход от макроскопического напряженно-деформированного состояния (НДС) к НДС на мезоуровне зерен осуществляется на основе гипотезы Фойгта. Сдвиговые деформации в матрице приравниваются к макродеформациям в композите. Более точные модели использовать затруднительно, так как модули сдвига волокон неизвестны.

Для уменьшения объема вычислительной работы, сокращения циклов обмена информацией между кодами, непрерывное изменение эффективных свойств УУКМ заменяется ступенчатым изменением. Для этого объем эндопротеза разбивается на малые области, в которых макродеформации почти постоянны и близки к максимальным (на каждом шаге). Модификация свойств композита в этих областях осуществляется по средним значениям макронапряжений. Области изменения свойств (редуцирования) (рис. 3, 4) выбираются на основе картин распределения полей макродеформаций и макронапряжений (рис. 6). Характерный размер конечного элемента в областях изменения свойств составляет 0,01 мм.

Зависимость P = f ( u ) в координатах сила реакции P [Н] – перемещение суставной головки u [мм], представлена на рис. 5.

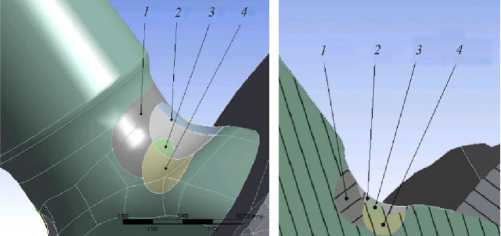
Первые повреждения появляются при нагрузке 1740 ньютонов в области № 1, представленной на рис. 3 и 4, b, в которой начинают выполняться критерии повреждения зерен (3)–(6). Размеры и границы области, где величины макродеформаций превышают значения, при которых происходят повреждения, определяются рассмотрением полей макродеформаций при сечении плоскостями параллельными и перпендикулярными плоскости зеркальной симметрии эндопротеза. После изменения эффективных свойств композита в этой области поля деформаций и напряжений в эндопротезе перераспределяются, сила реакции эндопротеза падает на 2,9 % до величины 1691 ньютон (первый локальный минимум на диаграмме).

а

b

Рис. 3. Расположение областей изменения свойств: 1 , 2 , 3 , 4 – области изменения свойств; а – аксонометрическая проекция, b – сечение плоскостью, проходящей через ось симметрии протеза

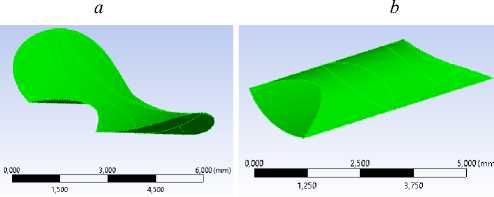
Fig. 3. Situation of properties change domains: 1 , 2 , 3 , 4 – properties change domains; a – axonometrical projection, b – cross-section by plane going through axis of endoprosthesis symmetry

На рис. 6, а , представлено распределение поля макродеформаций до перерасчета эффективных свойств УУКМ. Видно (рис. 6, b ), как перераспределились деформации после появления повреждений в области № 1 и перерасчета эффективных свойств. Форма и размеры области представлены на рис. 3, 4, c . При дальнейшем повышении нагрузки максимальные значения макродеформаций перемещаются в примыкающую область – область № 2. До нагрузки 2000 ньютонов новых повреждений не происходит. Повреждения в этой области начинают возникать с нагрузки 2000 ньютонов (рис. 5). После модификации свойств в этой области сила реакции эндопротеза падает на 1,25 % до 1975 ньютонов относительно величины второго локального максимума (2000 Н). Дальнейшее увеличение нагрузки в очередной раз приводит к перераспределению напряжений и деформаций, и максимальные значения перемещаются в область № 3. При нагрузке 2004 ньютонов наблюдается глобальный максимум на диаграмме (см. рис. 5), что соответствует предельному значению несущей способности эндопротеза ТБС по силовому фактору.

При дальнейшем увеличении нагрузки повреждения перемещаются в область № 3 и затем в область №4, начинается ниспадающая ветвь диаграммы нагружения

Начиная с величины перемещения суставной головки u = 1,78 мм, ПУ-матрица в 1, 2, 3-й и 4-й областях (выполняются все критерии (3)–(6)) продолжает оказывать механическое сопротивление только всестороннему сжатию. При этом матрица сохраняет сплошность, становясь аналогичной сыпучим гранулированным средам. При перемещении суставной головки на большую величину продолжится прогрессирующее снижение жесткости протеза за счет появления новых областей деградации свойств.

e

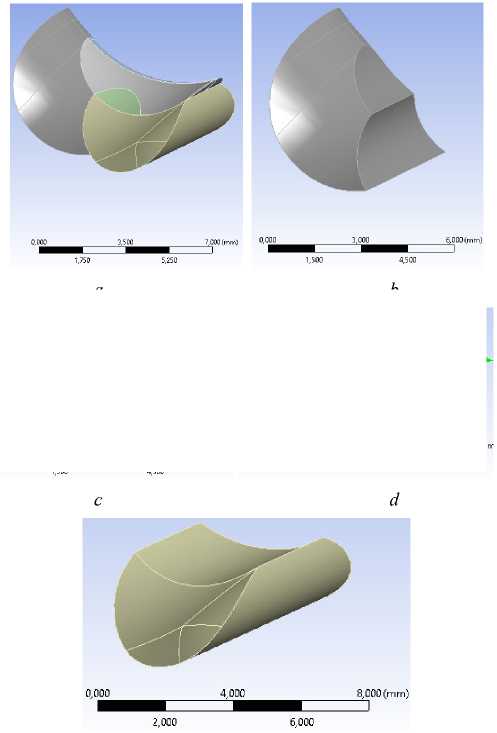
Рис. 4. Формы и размеры областей изменения свойств композита: а – общий вид областей изменения свойств, b – первая область, c – вторая область, d – третья область; e – четвертая область

Fig. 4. Shapes and sizes of composite property change domains: a – general view of property change domains, b – first domain, c – second domain, d – third domain, e – fourth domain

Р [Н]

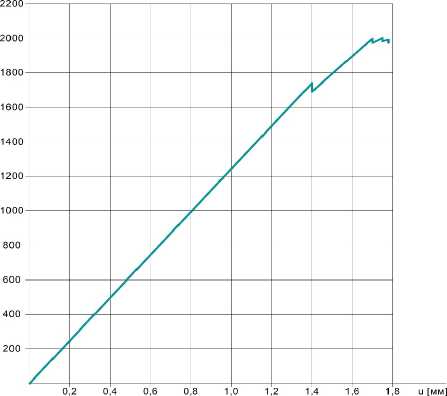
Рис. 5. Диаграмма нагружения эндопротеза ТБС

Fig. 5. Loading curve of the endoprosthesis

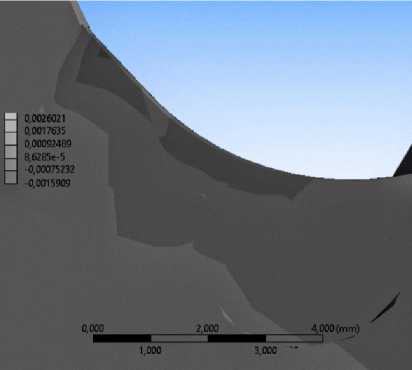
b

Рис. 6. Распределение полей сдвиговых деформаций в плоскости XY в области шейки эндопротеза ТБС: а – эффективные свойства не модифицированы (перемещение суставной головки 1,4 мм), b – эффективные свойства композита модифицированы (перемещение суставной головки 1,4 мм)

Fig. 6. Shear strains distribution on plane XY in endoprosthesis neck: a – nonmodified effective properties (joint head displacement 1.4 mm), b – modified effective properties (joint head displacement 1.4 mm)

Окончание диаграммы на рис. 5 соответствует перемещению 1,78 мм и силовой реакции 1976 ньютонов. Это перемещение можно условно принять за предельное значение деформативности эндопротеза. Она превосходит деформативность при штатной нагрузке 1850 ньютонов ( u = 1,54 мм ) на 16 %. При этом несущая способность по силовому фактору сохраняется, а заметная деформатив-ность указывает на механическую живучесть конструкции. Последовательное появление зон повреждений обусловливает нелинейное псевдопластическое деформирование эндопротеза.

Повреждения происходят в области перехода от посадочного конуса к шейке, как это и было обнаружено при проведении лабораторного испытания по нагружению эндопротеза, которое описано в работе [17]. В данном расчетном эксперименте углеродные волокна не разрушаются по причине того, что напряжения в них во много раз ниже, чем предел прочности волокна. Максимальная нагрузка, которую выдерживает эндопротез, равна 2004 Н при перемещении суставной головки на величину 1,75 мм. Величина наибольшей нагрузки, которую выдержал эндопротез при лабораторном испытании, приблизительно равна 1900 Н. Величина максимальной расчетной нагрузки по предложенной модели выше опытной на 5,47 %.

Заключение

В исследовании разработана модель деформирования эндопротеза из УУКМ с учетом процессов локальных повреждений. Эти повреждения возможны при перегрузках, вызванных случайными обстоятельствами. При штатных нагрузках разрушений не происходит. Выявлены зоны возможных повреждений в углерод-углеродном композиционном материале, из которого изготовлен эндопротез ТБС, рост этих зон. Моделирование позволило оценить несущую способность эндопротеза с учетом сложной структуры материала, показало его живучесть после случайных перегрузок.

Важное место в модели занимает описание деформирования пироуглеродной матрицы. ПУ-матрица сильно дефектна, обладает стохастической внутренней структурой, зерна ПУ имеют сильно анизотропные упругие и прочностные характеристики. В силу этого процесс разрушения (повреждаемости) матрицы имеет многостадийный характер, повреждения накапливаются постепенно, обусловливая нелинейное псевдопластическое деформирование самой матрицы и композита. Первые повреждения инициируются в зернах со специфическим окружением соседних зерен, в которых реализуются максимальные флуктуации мезодеформаций и мезонапряжений. В литературе такие группы зерен получили название экстремальных микроструктур или экстремальных кластеров [31; 32].

На основе синтеза инженерной расчетной модели, разработанной в программном комплексе ANSYS, и алгоритма, учитывающего сложную структуру УУКМ с повреждающейся ПУ-матрицей, была построена диаграмма зависимости силы реакции эндопротеза от перемещения суставной головки. Диаграмма является нелинейной, с появлением ниспадающей ветви после нагрузки в 2004 ньютона. Повреждение эндопротеза происходит растянуто по перемещениям головки протеза и не является катастрофическим.

Сохранение несущей способности конструкций из волокнистых композитов с полимерной матрицей после появления первичных разрушений является хорошо известным феноменом. Конструкции продолжают оказывать сопротивление даже после достижения максимальных нагрузок, проявляя так называемое закритическое деформирование. Проведенное моделирование показало, что эндопротез из УУКМ сохраняет это преимущество за счет специфических свойств ПУ-матрицы. Предельная деформация (по перемещению) на рис. 5 превосходит деформацию при штатной нагрузке на 16 %. При этом силовая реакция протеза все еще значительно превосходит