Lossy Compression Color Medical Image Using CDF Wavelet Lifting Scheme

Published Online September 2013 in MECS

The massive use of numerical methods in medical imaging (MRI, X scanner, nuclear medicine, etc…) today generates increasingly important volumes of data.

The problem becomes even more critical with the generalization of 3D sequence.

So it is necessary to use compressed images in order to limit the amount of data to be stored and transmitted.

Many compression schemes by transformation have been proposed, we can cite the standards JPEG images, MPEG1 and 2 for video compression.

All of these standards are based on the discrete cosine transform (DCT) [1].

Over the past ten years, the wavelets (DWT) have had a huge success in the field of image processing, and have been used to solve many problems such as image compression and restoration [2].

However, this representation is necessarily linear and this is a major drawback in describing real signals like natural images where discontinuities, edges and other singularities are numerous.

To overcome this problem, new multiresolution decompositions are better adapted to the representation of such signals have been introduced.

We introduce in this paper the evaluation of our compression algorithm based on lifting scheme [3] using the new parameters of judgment. For this reason, this paper is divided into three parts: the first is devoted to a representation of the Lifting scheme, and then we present the biorthgonal wavelet CDF 9/7.

The JPEG2000 choice for the lossy-to-lossless compression algorithm (JPEG2000-LS) is the DWT known as Gall 5/3, Spline 5/3, or CDF (2,2).

In order to evaluate image compression by our algorithm, we compare evaluation parameters results obtained with the existing techniques namely the wavelets filter bank and Gall5/3 lifting scheme.

The paper has organized as section I introduction, section II introduce and explain the wavelet transform based on lifting scheme; section III is presented the bi-orthogonal wavelet CDF9/7 lifting scheme , section IV presented the SPIHT coding ,section V we proposed the evaluated quality of image compression ; The proposed algorithm is described in Section VI ; After that, application of the proposed algorithm is discussed in section VII, and we draw our conclusion in the last section, and finally the references.

• II.    WAVELET TRANSFORMS

The wavelet transform (WT), in general, produces floating point coefficients. Although these coefficients are used to reconstruct an original image perfectly in theory, the use of finite precision arithmetic and quantization results in a lossy scheme.

Recently, reversible integer WT's (WT's that transform integers to integers and allow perfect reconstruction of the original signal) have been introduced [ 4, 5].

In [6], Calderbank and al. introduced how to use the lifting scheme presented in [7], where sweldens showed that the convolution based biorthogonal WT can be implemented in a lifting-based scheme as shown in Fig.1 for reducing the computational complexity.

Note that only the decomposition part of WT is depicted in Fig.1 because the reconstruction process is just the reverse version of the one in Fig .1.

The lifting-based WT consists of splitting, lifting, and scaling modules and the WT is treated as prediction-error decomposition.

It provides a complete spatial interpretation of WT.

In Fig .1, let X denote the input signal, and XL1 and X H1 be the decomposed output signals, where they are obtained through the following three modules of lifting based 1DWT:

• 1.    Splitting: In this module, the original signal X is divided into two disjoint parts, i.e., Xe(n)=X(2n) and X0(n)=X(2n+1) that denote all even-indexed and odd-indexed samples of X , respectively [8].

• 2.    Lifting: In this module, the prediction operation P         is used to estimate X0(n) from Xe(n)

• 3.    Scaling: A normalization factor is applied to d(n) and s(n), respectively. In the even-indexed part s(n) is multiplied by a normalization factor Ke to produce the wavelet subband XL1 .

and results in an error signal d(n) which represents the detailed part of the original signal.

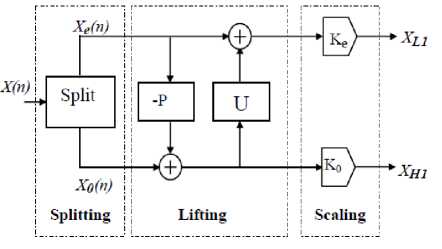
Figure. 1 The Lifting -based wavelet

Then we update d(n) by applying it to the update operation U, and the resulting signal is combined with Xe(n) to s(n) estimate, which represents the smooth part of the original signal.

Similarly in the odd-index part the error signal d(n) is multiplied by K0 to obtain the wavelet subband XH 1 .

Note that the output results of XL 1 and XH 1 obtained by using the lifting-based WT are the same as those of using the convolution approach for the same input even if they have completely different functional structures.

Compared with the traditional convolution-based WT, the lifting-based scheme has several advantages. First, it makes optimal use of similarities between the highpass and lowpass filters; the computation complexity can be reduced by a factor of two.

Second, it allows a full in-place calculation of the wavelet transform. In other words, no auxiliary memory is needed.

• III.    BIORTHOGONAL WAVELETS CDF9/7

This article deals with biorthogonal wavelet 9/7. These wavelets are part of the family of symmetric biorthogonal wavelet CDF. The low pass filters associated with wavelet 9/7 have p=9 coefficients in the analysis, p=7 coefficients to synthesize, as described in table1.

The wavelets 9/7 have a great number of null moments for a relatively short support. They are more symmetrical and very close to orthogonality. This is an important feature in coding which ensures that the reconstruction error is very close to the quantization error in terms of mean squared error. Antonini and Barlaud were the first [9] to show the superiority of the biorthogonal wavelet transform 9/7 for the decorrelation of natural images. It has been widely used in image coding [10],[11] and is used by the JPEG-2000 codec [12].

Table1 a : The analysis filter coefficients.

Analysis filter coefficients
/	Low-pass filter	High-pass filter
0	0.6029490182363579 0.6029490182363579	+ 1.115087052457000
±1	+ 0.266864118442875	+ 0.591271763114250
±2	- 0.078223266528990	-0.057543526228500
±3	-0.016864118442875	-0.091271763114250
+4	+ 0.026748757410810

Table 1 b : The synthesis filter coefficients.

Synthesis filter coefficients
i	Low-pass filter	High-pass filter
0	+ 1.115087052457000	0.6029490182363579
11	-0.591271763114250	-0.266864118442875
-2	- 0.057543526228500	-0.078223266528990
±3	+ 0.091271763114250	+ 0.016864118442875
+4		+ 0.026748757410810

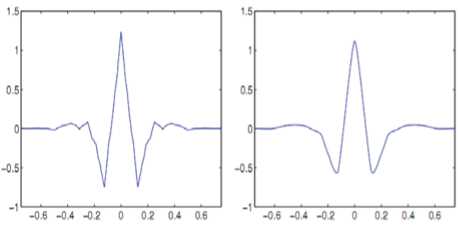
Figure. 2 CDF 9/7 wavelet v and v dual.

The Lifting scheme of the biorthogonal transform 9/7 goes through of four steps: two prediction operators and two update operators as shown it Fig.3. [13, 14].

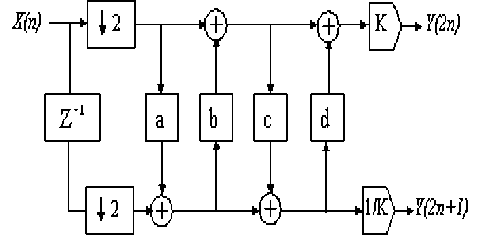
Figure. 3 Lifting implementation of the analysis side of the CDF 9/7 wavelet

The synthesis side of the filter bank simply inverts the scaling, and reverses the sequence of the lifting and update steps.

Fig .4 shows the synthesis side of the filter bank using lifting.

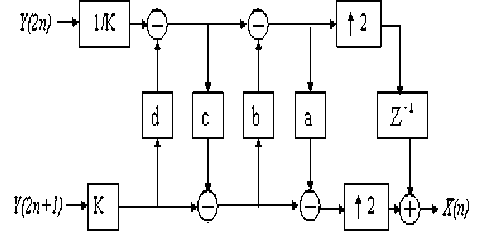
Figure. 4 Lifting implementation of the synthesis side of the CDF 9/7 filter bank

• IV.    SPIHT CODING SCHEME

When the decomposition image is obtained, we try to find a way to code the wavelet coefficients into an efficient result, taking redundancy and storage space into consideration.

SPIHT [8] is one of the most advanced schemes available, even outperforming the state-of-the-art JPEG 2000 in some situations.

The basic principle is the same; a progressive coding is applied, processing the image respectively to a lowering threshold.

The difference is in the concept of zerotrees (spatial orientation trees in SPIHT).

This is an idea that takes into consideration bounds between coefficients across subbands at different levels [10].

The first idea is always the same: if there is a coefficient at the highest level of the transform in a particular subband which considered insignificant against a particular threshold, it is very probable that its descendants in lower levels will be insignificant too.

Therefore we can code quite a large group of coefficients with one symbol.

Fig.5 shows how a spatial orientation tree is defined in a pyramid constructed with recursive four subbands splitting. The coefficients are ordered hierarchically.

According to this relationship, the SPIHT algorithm saves many bits that specify insignificant coefficients [15].

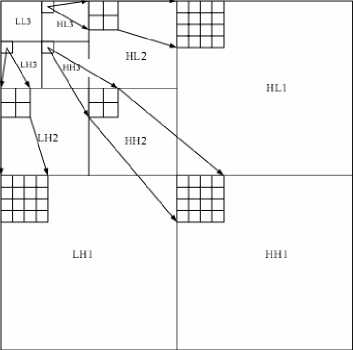
Figure.5- Parent-child relationship

• V.    COMPRESSION QUALITY EVALUATION

The Peak Signal to Noise Ratio (PSNR) is the most commonly used as a measure of quality of reconstruction in image compression.

The PSNR were identified using the following formulae:

MSE

1 MxN

i = NJ = M2

X ill(i, J ) - I(I, J ))

1=1        J=1 ''

Mean Square Error (MSE) which requires two MxN grayscale images I and ^I where one of the images is considered as a compression of the other is defined as:

The PSNR is defined as:

PSNR = 10 log,, ( ⁽ Dynamics of image ) 2 1 (2) ¹⁰ ( MSE )

Usually an image is encoded on 8 bits. It is represented by 256 gray levels, which vary between 0 and 255, the extent or dynamics of the image is 255.

• • The structural similarity index (SSIM):

The PSNR measurement gives a numerical value on the damage, but it does not describe its type.

Moreover, as is often noted in [16,17], it does not quite represent the quality perceived by human observers. For medical imaging applications where images are degraded must eventually be examined by experts, traditional evaluation remains insufficient.

For this reason, objective approaches are needed to assess the medical imaging quality.

We then evaluate a new paradigm to estimate the quality of medical images, specifically the ones compressed by wavelet transform, based on the assumption that the human visual system (HVS) is highly adapted to extract structural information.

The similarity compares the brightness, contrast and structure between each pair of vectors, where the structural similarity index (SSIM) between two signals x and y is given by the following expression [18,19]:

SSIM (x, y) = l(x, y).c(x, y).s(x, y) (3)

Finally the quality measurement can provide a spatial map of the local image quality, which provides more information on the image quality degradation, which is useful in medical imaging applications.

For application, we require a single overall measurement of the whole image quality that is given by the following formula:

MSSIM ( I , I) =-^ %SSIM ( I , ,I i ) (4)

Where I and I ^ˆ are respectively the reference and degraded images, I_i and I_i are the contents of images at the i-th local window. M: the total number of local windows in image. The MSSIM values exhibit greater consistency with the visual quality.

• VI.    ALGORITHM

Before applying CDF 9/7 biorthogonal wavelet technique on the retinographic color images, the RGB color images are converts into YCbCr form, and then applying CDF 9/7 technique on each layer independently, this means each layer from YCbCr are compressed as a grayscale image.

Fig.6 shows CDF 9/7 applied on each YCbCr layer.

YCbCr refers to the color resolution of digital component video signals, which is based on sampling rates. In order to compress bandwidth, Cb and Cr are sampled at a lower rate than Y, which is technically known as "chroma subsampling."

This means that some color information in the image is being discarded, but not brightness (luma) information.

Y = 0.2989 x R + 0.5866 x G + 0.1145 x B

Cb =-0.1687 x R - 0.3312 x G + 0.5 x B

Cr = 0.5 x R - 0.4183 x G - 0.0816 x B

When the decomposition image is obtained, we try to find a way to code the CDF97 wavelet coefficients into an efficient result, taking redundancy and storage space into consideration.

After, we apply SPÏHT algorithm on each layer (y,Cr,Cb) independently . This process is repeated for every resolution in the case of level 6 decompositions.

The encoding / decoding can be terminated at any time, with the best reproduction obtained up to that point.

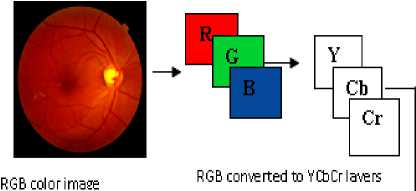
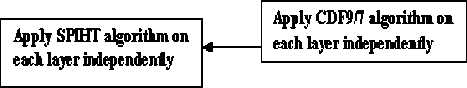
Figure.6 Complete steps image compression Technique using CDF97 coupled with SPIHT

• VII.    RESULTS AND DISCUSSION

We are interested in lossy compression methods based on 2D wavelet transforms more particularly the lifting scheme because their properties are interesting.

Indeed, the 2D wavelets transform combines good spatial and frequency locations. As we work on medical image, the spatial location and frequency are important [29, 30].

We applied the proposed algorithm on the test color medical image 'retinographic' of size 512x512 x 3encoded by 8bpp.

This image is taken from the GE Medical System database [22].

Figure.7 Original color image

The importance of our work lies in the possibility of reducing the rates for which the image quality remains acceptable.

Estimates and judgments of the compressed image quality are given by the PSNR evaluation parameters and the MSSIM similarity Index.

Fig.8 shown below illustrates the compressed image quality for different bit-rate values (number of bits per pixel). According to the PSNR and MSSIM values, we note that from 0. 5bpp, image reconstruction becomes almost perfect.

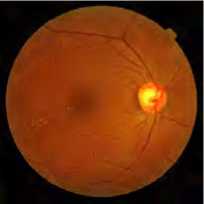
R=0.125bpp, PSNR=34.94, MSSIM=0.797

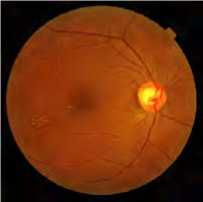
R=0. 25bpp, PSNR=34.97, MSSIM=0.815

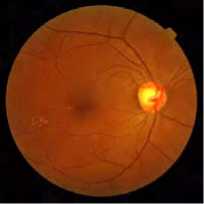
R=0. 5bpp, PSNR=37.95, MSSIM=0.870

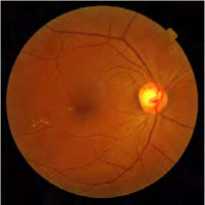
R=0. 75bpp, PSNR=38.51, MSSIM=0.89

R=1 bpp, PSNR=38.83, MSSIM=0.901

R=2 bpp, PSNR=43.29, MSSIM=0.956

Figure.8 Retinographic image compressed with CDF9/7 (Lifting Scheme) and SPIHT coding

To show the performance of the proposed method, we make a comparison between these different types of transform (CDF9/7 (Filter bank); spline 5/3 (lifting scheme) and CDF9/7 (lifting scheme)) coupled with SPIHT coding and CDF9/7 (lifting scheme) combined with the EZW coding, which we calculate the various parameters (PSNR, MSSIM) in order to study the influence of coding choices on color medical images.

For each application we vary the bit-rate from 0.125 to 2, and we calculate the PSNR and MSSIM.

The results obtained are given in Table 2 and Table 3.

TABLE 2

Rc (bpp)	CDF9/7(lifting)+ SPIHT		spline5/3(lifting) +SPIHT
	PSNR	MSSIM	PSNR	MSSIM
0.125	34.75	0. 79	31.53	0.78
0.25	34.97	0.81	34.51	0.80
0.5	37.95	0.87	34.93	0.83
0.75	38.51	0.89	36.08	0.86
1	38.83	0.90	35.62	0.87
1.5	42.33	0.94	35.48	0.88
2	43.29	0.95	35.28	0.88

TABLE 3

Rc (bpp)	CDF9/7 (filter bank)+SPIHT		CDF9/7(lifting) +EZW
	PSNR	MSSIM	PSNR	MSSIM
0.125	32.90	0.74	32.40	0.68
0.25	33.55	0.79	33.02	0.70
0.5	35.70	0.80	35.64	0.78
0.75	36.89	0.84	36.70	0.82
1	37.65	0.88	37.32	0.87
1.5	39.88	0.89	39.25	0.88
2	41.32	0.93	40.90	0.92

The comparison in terms of image quality for the four algorithms is given by the PSNR and MSSIM curves represented in Fig.9 and Fig.10.

These results are obtained with a 0.5 bpp bite-rate. We note that our algorithm is adapted for the Retinographic medical image compression.

We can observe that compression degrades to a lessen extent the image structure for a low compression bit-rate.

However, for high compression bit rate, our algorithm better safeguards the various image structures.

Comparing the different values of PSNR and MSSIM, we show clearly the efficiency of our algorithm in terms of compressed image quality for the low bit-rate.

These images were tested on Intel Core (I3) 2.13 GHz PC with 2GB of RAM using Matlab 2009.b.

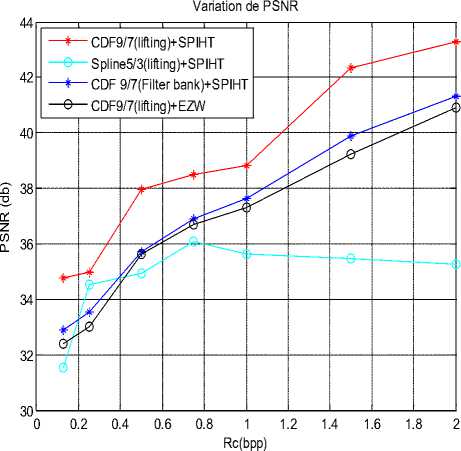
Figure .9 PSNR variation using different methods

Original color image: frottis sanguin

Rc=0.5 bpp

TC=93.75% ------►

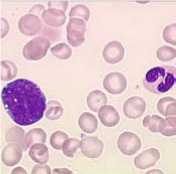
CDF9/7(Lifting Scheme)+SPIHT PSNR=38.25 db, MSSIM=0.92

Figure. 11 Compressing of different slices by CDF9/7 (Lifting Scheme) and SPIHT Coding.

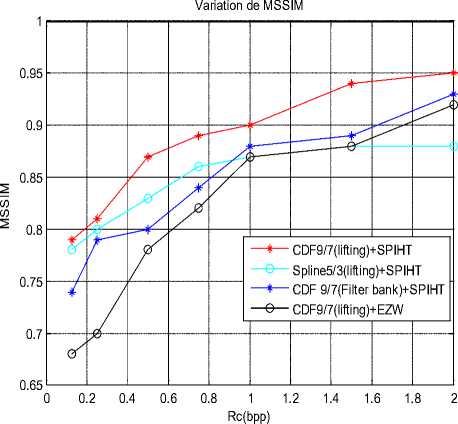
Figure.10 MSSIM variation using different methods

• VIII.    CONCLUSIONS

The objective of this paper is undoubtedly the quality assessment of color medical Images after the compression step.

The latter is regarded as an essential tool to aid diagnosis (storage or transmission) in medical imaging.

We used the Biorthogonal CDF9/7 wavelet compression based on lifting scheme, coupled with the SPIHT coding.

After several applications, we found that this algorithm gives better results than the other compression techniques.

We have noticed that for 0.5 bpp bit-rate (TC=93.75%), the algorithm provides very important PSNR, MSSIM, values for color medical images and it is more suitable for this category of images.

Thus, we conclude that the results obtained are very satisfactory in terms of compression ratio and compressed image quality.

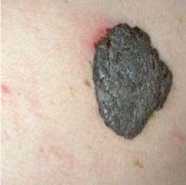
Original color image: benign

Rc=0.5 bpp

TC=93.75%

------►

CDF9/7(Lifting Scheme)+SPIHT

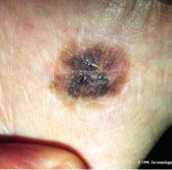
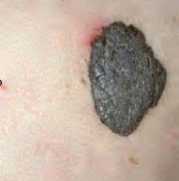
Original color image: melanoma

PSNR=34.09 db, MSSIM=0.917

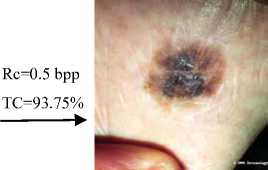
CDF9/7(Lifting Scheme)+SPIHT

PSNR=37 db, MSSIM=0.933