Lossy Compression of Color Images using Lifting Scheme and Prediction Errors

Published Online April 2016 in MECS DOI: 10.5815/ijmecs.2016.04.01

In today’s world, the massive exchange of digital information such as audio, video and images over internet and in mobile phones has brought a lot of interest in the field of data compression. Image compression is basically the method of reducing the total amount of original image data to another lesser quantity of data. Compression techniques can be broadly classified as: lossless and lossy techniques. In the first approach, the total amount of image data is reduced without any loss in the quality of reconstructed image while in the second one, total amount of original data is reduced with some degradation in the quality of reconstructed images, however, that information loss is not perceptually visible to human eyes. The implementation of lossy compression methods is eventually of good use because of large storage or bandwidth requirements of digital images.

Plenty of work has been reported in literature for lossless compression including standard and independently techniques. Among the variety of work reported in literature, the most widely used may be lossless JPEG [1], JPEG-LS [2], LOCO-I [3], CALIC [4], JPEG2000 [5] and JPEG-XR [6] etc. For color images, it is well known, that the primary color components i.e. Red (R), Green (G) and Blue (B) are highly correlated which is an indication of repeated information in more than one image components. For compression of color images, it is an intelligent practice to reduce the correlation among these RGB planes using any transformation from RGB to some less correlated color space and then each of the less correlated color component is independently compressed. An attempt of compressing each of the RGB color space without transformation adds an unnecessary overhead of compression of repeated information more than once. The correlation among the RGB planes can be reduced by using transformations such as: YCbCr [34], YCuCv [35], KLT [36], YIQ [37], O1O2O3 [11] and YCoCg and YCoCg-R [38]. Out of these color space transformations, YCbCr is used most frequently in lossy compression of color images. Many variants of RGB to YCbCr transformation exist, among those the one is used in lossy JPEG2000 standard. Recently, another such color space transformation (YCoCg-R) is used in JPEG-XR [6] standard. It is found in literature [34] that the computational complexity of YCoCg-R is lower than YCbCr. Hence it can compress color images more efficiently with lower computational complexity.

Lossy compression of color images is also attracting lot of interest in the greed of good compression performance. A lot of work has been reported in literature for lossy compression of color images viz. methods based on direct processing of image samples such as block truncation coding (BTC) [8, 11, 12] and other techniques are build around vector quantization (VQ) [15, 16]. The BTC [7] based compression techniques can be applied to each of the color planes to reduce the total data amount. Wu et al. [9] proposed a single bit map BTC (SBBTC) technique for compression of color images using a single bit map to quantize all the three color planes. In SBBTC method, when 4×4 block size is used then bit rate is 4 bit per pixel (bpp), however, for BTC it is 6 bpp. Another SBBTC method is proposed by Kurita et al. [8], which creates the single bit map (SBM) by applying an adaptive one bit VQ. Tai et al. [10] proposed SBBTC method using Hopfield neural network (HNN) to create a SBM of a block. Another SBM based method called CICMPBTC is proposed by Yang et al. [12], which is based on the principle of moment preserving. An improved version of CICMPBTC method called CICMPBTC* is proposed by considering few points: (a) each color plane is quantized from 8 bit to 5 bit and (b) a set of predefined 64 bit maps is selected. A similar method which uses the predefined set of bit maps is also used in [13]. It is sure that the use of BTC on each color plane gives good quality of reconstructed images but at the same time it results higher bit rate. Hence to achieve much lower bit rate with some slight degradation in the quality of reconstructed images an another method based on BTC using pattern filling (BTC-PF) is proposed by Bibhas et al. [11], in this method the correlation among RGB plane is reduced using RGB to O1O2O3 transformation. Each of of the transformed O1, O2 and O3 plane is compressed using BTC-PF with different values of parameter, Bibhas et al. [11] named this method as CBTC-PF.

For color images, lossy compression techniques give better result in the transform domain using transformations such as Discrete Cosine Transformation (DCT) [17, 18, 19], Discrete Wavelet Transform (DWT) [20, 21, 22, 39, 40], Principal Component Analysis (PCA) [23] and Integer Wavelet Transform (IWT) [33]. The advantage of processing the information in transformed domain is due to the concentration of whole image information in just few numbers of transformed coefficients. Among the transformation discussed above, DCT has good energy compaction property, which plays a vital role in compression but it has a disadvantage of blocking artifacts, which occur when coarse coefficients are discarded. To avoid the blocking artifacts and to achieve better compression performance, DWT has come under consideration. Due to the multi-resolution property, DWT is used more frequently in many image compression techniques. It is used even in an image compression standard JPEG2000. Generally most of the DWT based compression techniques supports embedded bitstreams, which means that the quality of reconstructed image can be improved by sending more bits to the decoder. Several wavelet based compression techniques are reported in literature such as Embedded Zerotree Wavelet (EZW) [24], Set Partitioning in Hierarchical Trees (SPIHT) [25], Embedded Block Coding with Optimized Truncation (EBCOT) [26], Wavelet Difference Reduction (WDR) [27] etc. EZW algorithm was one of the first algorithms introduced by Shapiro [24], which shows the full power of wavelet in image compression. EZW algorithm is fast to perform but it cannot achieve good compression performance. Therefore, Said and Pearlman [25] proposed an improved version of EZW, called SPIHT. In SPIHT, Hierarchical Trees refers to the quadtree of EZW and Set Partitioning refers to the way by which these quadtrees are divided at a given threshold. The most important characteristic of SPIHT is the way by which zerotree data structure is exploited to encode an entire insignificant region of a given bit plane with only one symbol. A lot of embedded wavelet based image compression techniques were developed which adopt zerotree data structure, but there exists few techniques, which are not based on zerotrees, one of the techniques among these is WDR algorithm [27]. In WDR coding, zerotree data structure is precluded but the embedding principles of lossless bit plane coding and set partitioning are preserved [28]. The coding performance of WDR is similar to that of SPIHT but to improve rate distortion performance, Walker [29] introduced parent-children relationship in the WDR algorithm. Later, Walker and Nguyen [30] incorporated siblings into the encoding in addition to the parentchildren relationship. In spite of having embedded bit stream feature, DWT has a disadvantage of processing the information in floating point numbers i.e. wavelet coefficients obtained after applying DWT are floating point numbers, due to which it would be difficult to achieve lossless compression in many application scenarios such as medical images where lossless compression is required for diagnostic investigation and analysis. Recently, a Lifting Scheme (LS) based IWT is proposed [33], which is the implementation of DWT. IWT has following advantages: first, a perfect reconstruction of compressed data is possible, without any information loss, which is desirable in many application scenarios such as medical images. Second, the computational complexity of IWT is lower than DWT. Finally, the use of IWT reduces the memory requirement, which is indeed necessary for fast transmission and storage.

It is obvious that the compression techniques based on transform domain (using transformations such as DCT, DWT, KLT, IWT etc.), results good compression performance over spatial domain (BTC and VQ) compression techniques, because in transformed domain most of the image information lie in just few number of transformed coefficients, which results good compression performance on quantization and entropy coding. Therefore, to achieve better compression performance, a color image compression algorithm is proposed by Fouzi et al. [14] which is based on DCT transform combined to an adaptive block scanning. The work reported in [14] achieved better compression performance over the previous discussed methods but due to use of block based DCT blocking artifacts may occur, when large number of DCT coefficients is discarded. Therefore, still there is a need to improve the compression performance while maintaining the good visual quality of compressed images.

In this paper, a color image compression technique using IWT in YCoCg-R color space is proposed. This technique is proposed to achieve much better compression performance in YCoCg-R color space using IWT along with an effective quantizer. The input image is first transformed from RGB color space to YCoCg-R color space, this transformation is used to reduce the correlation among these RGB planes. IWT is applied on each of the transformed color plane, which results an approximation and several detail subimages for each plane. Data amount of the approximation and detail subimages of all color planes are reduced using prediction error and an effective quantizer respectively, the optimal number of bits are assigned to each of the reduced data to achieve the compressed bit streams.

The rest of the paper is organized as follows: a brief overview of some terms related to proposed work are given in section II, the proposed compression and decompression scheme is described in section III, comparison of proposed work over several existing techniques is reported in section IV. Section V concludes the proposed work with its future scope.

• II.    Terms Related to Proposed Work

• A.    Integer Wavelet Transform

In conventional DWT, wavelet filters have floating point (FP) coefficients, so the truncation or rounding of FP values of the coefficients, to make the values integer, may cause some loss in original image information, due to the truncation or rounding, the wavelet coefficients can not be obtained in their full accuracy. To overcome this problem an integer to integer wavelet transform (IWT) is proposed by Sweldens et al. [31, 32, 33]. The LS based transform, which is an implementation of DWT, called IWT, works efficiently for compression of color images. IWT exploits the redundancy between low and high pass filters, which is necessary for compression of image. IWT maps the integer data to another integer data. In IWT, there is no loss of data in forward and inverse transformation. Therefore , lifting scheme is one of the methods used to perform integer wavelet transform. The demonstration of LS for the implementation of IWT is as follows:

where, s j_,n and d j_,n represent the n^th low and high frequency of wavelet coefficients at j^th level respectively. For j = 0, s 0,n shows the n^th value itself. ⌊.⌋ represents the rounding function, which rounds . to nearest integer towards minus infinity.

• B.    RGB to YCoCg-R Transform

It is used in recent compression standard JPEG-XR. The reversible mapping of YCoCg-R transform between Red-Green-Blue (RGB) and luma-chroma with integer arithmetic makes it suitable candidate for lossless color image compression. As reported in [34] that the YCoCg-R transform can improve the coding gain over YCbCr with lower computational complexity, therefore using YCoCg-R as a preprocessing step helps to improve the compression performance with less computation. In the proposed work, the use of YCoCg-R transform is to reduce the correlation among these RGB planes with low computational complexity.

RGB to YCoCg-R is expressed as:

Y		1/4	1/2	1/4	R
Co	«	1	0	- 1	G
Cg		- 1/2	1	- 1/2	B

The inverse transformation i.e. YCoCg - R to RGB is expressed as:

d 1, n = ⁵ 0,2 n + 1

⁵ 1, n = ⁵ 0,2 n ⁺

s 0,2 n

^{+ 5} 0,2 n + 2

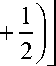
' 1, n - 1 ⁺ d 1, n ⁺ -

This section describes the proposed scheme for input image of size MXN. For an image of size M X N, there would be total T number of pixels, where T = MX N. The schematic figure of proposed work is shown in fig. 1 and the steps for image compression and decompression are shown in table-1 and 2 respectively .

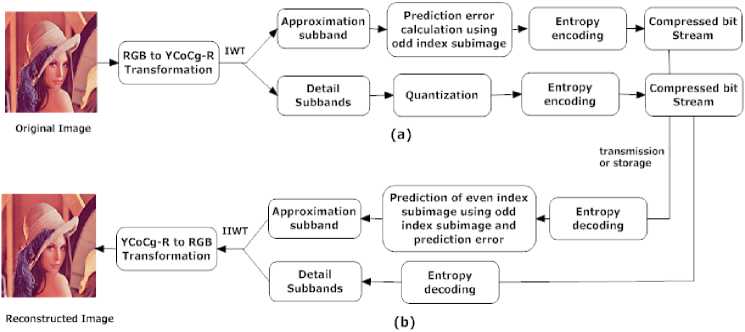
Fig.1. Proposed Scheme (a) Compression phase (b) Decompression phase

" R"		1	1/2	- 1/2"	" Y "	(4)
G	«	1	0	1/2	Co
. b _		. 1	- 1/2	- 1/2	. Cg _

A. Image Compression

For compression of a color image, original image is decomposed into three planes Red (R), Green (G) and Blue (B), the correlation among R, G and B planes is reduced using RGB to YCoCg-R transformation (explained in subsection B ), and then three level Integer wavelet Transform (IWT) is applied on all the three transformed color planes independently, it decomposes the each color space into ten subbands: an approximation and nine detail subbands as shown in fig. 2. Detail subbands of each level are collected to make the data sets DS l ( l = 0; 1; 2). Clearly, detail wavelet subbands of each consecutive level have 3T/4, 3T/16, 3T/64 number of detail information respectively. By this multi-level decomposition using IWT, original image can be represented by A , DS ₀ , DS ₁ and DS ₂ .

Due to the spatial correlation of neighbouring pixels the values of even and odd row subimages are not too much different, which results small values in prediction error.

Now, Huffman coding is applied on each of the prediction errors for all the three planes and also on the subimage S _o , to get the reduced amount of original image data. Each of the detailed subbands of all the three transform color space are quantized using an effective quantizer as:

L = 2 b

255 r=

L

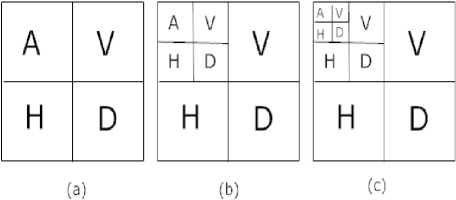
Fig.2. Integer wavelet decomposition (a) First level (b) Second level (c) Third level

Q 1 ( i , j) = round (

DS^j ) ₊ o.5

r

* r )

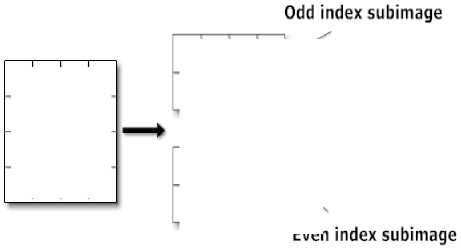
Fig.3. Input image and decomposition of even and odd indexed pixel values.

where, b = 1,2,....8.

Q l ( i , j ) represents the quantized detail coefficients and r is a quantizing parameter its value depends on L . For b = 8, each of the detail subbands for all the color space can be reconstructed losslessly, further optimal number of bits are assigned to each of the quantized detail subbands using Huffman coding, which results compressed bit streams.

Representing the total amount of compressed data obtained from all sub-images of each plane by B . Hence, the compression ratio (CR) i.e. the ratio between the original image data to the compressed data (measured in bits) is expressed as:

CR =

Size of original color image in bits Size of compressed data in bits ( B )

and bit per pixel (bpp) is expressed as:

24 bpp =--

CR

To achieve the better prediction error, the approximation subband A of all the three color space are divided into two subimages as shown in fig. 3: a group of pixels positioned at even row index S e and another group of pixels positioned at odd row index S o . Subimages S o and S e are used to calculate the prediction error (E).

Decomposition of approximation subband is achieved as:

So (i, j) = A(2i-1, j)

Se (i, j) = A(2i, j)

Now prediction error is calculated as:

E(i, j) = SE (i, j) - So (i, j)(7)

• Table 1.    Steps for compression

• 1    d ecompose a color image into its primary color components i.e. r ed (R), Green(G) and Blue (B).

• 2    a pply rgb to yc o c g -r transform to reduce the correlation among the RGB planes.

• 3    a pply three level iwt on each of the transformed planes independently, which results an approximation and nine detail wavelet subbands.

• 4    d ecompose the approximation subbands of each of the transformed planes into two subimages: an odd and even index subimages.

• 5    c alculate the prediction errors i.e. the difference between even and odd indexed subimages.

• 6    a pply the h uffman coding, on each of the odd index subimage and prediction errors obtained from all the three transformed color planes.

• 7    r educe the data amount of each of the detail subbands using an effective quantizer.

• 8    a pply the h uffman coding, which assigns the optimal codes to each of the quantized data obtained from step 7.

• Table 2.    Steps for decompression

• 1.    Decompose the compressed bit streams obtained from all the three color planes.

• 2.    For approximation subband: apply Huffman decoding on compressed bit streams, which results odd index subimage along with prediction errors.

• 3.    Use the odd index subimage and prediction errors obtained in step 2, in order to predict the intensity values of even index image.

• 4.    Now, odd and even index subimages are merged to get the approximation subband.

• 5.    For detail subbands: apply the Huffman decoding, on each of the compressed bit streams, which results reconstructed detail subbands.

• 6.    Collect the approximation and detail subbands obtained from steps 4 and 5.

• 7.    Apply Inverse IWT on reconstructed approximation and detail subbands, to get the the reconstructed color planes.

• 8.    Step 7 results, reconstructed Y, Co and Cg planes.

• 9.    Collect the three transformed color planes obtained in step 8 and apply the YCoCg-R to RGB transform.

• 10.    Finally, the reconstructed image (I’) is obtained by combining all the three color planes obtained from step 9.

• B. Image Reconstruction

Decompose the compressed bit streams obtained from approximation and several detail subbands of all the three transformed color planes. For approximation subbands, when having compressed bit streams we can get the reconstructed subimages by applying the Huffman decoding on compressed bit streams, which results odd index subimages S_o of all the three color planes along with the prediction errors of each plane. Reconstructed subimage S_o and prediction errors E help to get the reconstructed subimage S e as:

S e ( i , j ) = S o ( i , j ) + E ( i , j )               (13)

Now approximation subimages of all the three color space can be reconstructed losslessly as:

R (2i - 1, j) = S o ( i , j)                (14)

Clearly, R represents the approximation subband at 3rd level. Now, to get the reconstructed detail subbands, Huffman decoding is applied on each of the compressed bit streams obtained from several quantized detailed subbands at their respective levels, for b = 8 the reconstructed image can be obtained without any loss. Further, the Inverse of Integer Wavelet Transform (IIWT) is applied on approximation and detail subbands to get the reconstructed image I‘ .

The quality of reconstructed image can be measured mathematically using measures such as: Mean Squared Error (MSE), Peak Signal to Noise Ratio (PSNR). The MSE is defined as cumulative squared error between the original and reconstructed images and is expressed as:

1    M - 1 N - 1                         ²

^MSE =      2 2⁽ I ( i , j ) - I (i , j ) )      ⁽¹⁶⁾

MN i = 0 j - 0

where, I ( i , j ) and I^’ ( i, j ) are the original and reconstructed images both of size M X N respectively. For gray scale images, PSNR is expressed as:

PSNR = 10log_lo-55-             ⁽¹⁷⁾

However, for the color image, PSNR is expressed as:

PSNR = 10log_lo---------255_^3---------

¹⁰ MSE ( R ) + MSE ( G ) + MSE ( B )

• IV. Experimental Results

To test the efficiency of proposed work over the various existing techniques, we have used several test images such as: Lena, Peppers, Airplain each of size 512 X 512, and Girl, Couple, House and Zelda of size 256 X 256. The test images used in our work are publicly available at

R (2i , j ) = S e ( i , j )                   (15)

Table 3. Performance comparison of proposed work with some existing methods on various test images

Proposed Scheme			Scheme in [14]		WDR [27]		SPIHT [25]		JPEG2000
Images	PSNR	bpp	PSNR	bpp	PSNR	bpp	PSNR	bpp	PSNR	bpp
Airplane	30.66	0.4799	30.381	0.5917	30.28	0.9114	30.06	0.6304	30.46	0.4899
Peppers	31.05	0.5659	30.059	0.809	30.21	0.8987	29.75	0.8011	30.99	0.5694
Lena	32.99	0.5058	31.97		32.48	1.4434	32.64	1.0505	32.76	0.6903
Girl	35.89	0.4281	35.002	0.4574	35.17	1.0176	35.52	0.7708	35.45	0.7043
Couple	32.96	0.5970	32.287	0.9252	32.44	1.99	32.70	1.33	32.01	0.6204
House	32.76	0.5191	31.726	0.8232	32.29	1.7466	32.36	1.3722	32.20	0.7004
Zelda	31.98	0.6001	31.333	0.8705	31.67	0.6805	30.65	0.6260	31.70	0.6010
Average	32.61	0.5280	31.82	0.7553	32.08	1.1012	31.95	0.9401	32.22	0.6251

Table 4. Performance comparison of proposed work with varying quantization bit rate

B	7			6			5			4			3
Images	PSNR bpp		CR	PSNR bpp		CR	PSNR	bpp	CR	PSNR	bpp	CR	PSNR  bpp	CR
Airplane	43.58	1.3486	17.79	41.22	1.0041	23.90	37.96	0.6984	34.37	34.07	0.5422	44.26	30.11 0.4779	50.22
Peppers	43.58	1.6409	14.63	40.81	1.2834	18.69	36.77	0.9396	25.54	32.54	0.6767	35.78	28.92 0.5315	45.15
Lena	43.71	1.4828	16.18	40.87	1.1331	21.18	37.06	0.8016	29.94	33.16	0.5750	41.74	29.64 0.4798	50.02
Girl	43.34	1.1321	21.20	42.05	0.8194	29.28	40.19	0.6088	39.42	36.77	0.5321	45.11	32.88 0.5139	46.71
Couple	43.55	1.4682	16.35	41.18	1.1095	21.63	37.75	0.8005	29.98	33.67	0.6278	38.23	29.66 0.5577	43.04
House	43.58	1.3486	17.79	41.22	1.0041	23.90	37.96	0.6984	34.37	34.07	0.5422	44.26	30.11 0.4779	50.22
Zelda	43.55	1.5230	15.75	41.24	1.1749	20.43	37.85	0.8450	28.40	33.81	0.6546	36.69	30.41 0.5734	41.85

The efficiency of proposed work is evaluated by comparing it with several techniques such as wavelet based compression techniques: SPIHT, WDR, scheme reported in [14] and state of art compression technique i.e. JPEG2000. Compression performance is measured using bit per pixel (bpp) and quality of reconstructed image is measured using PSNR. The results obtained on comparing the proposed work with several existing methods are reported in table-3, when proposed work is compared with recent published work [14], WDR [27], SPIHT [25] and JPEG2000, it gives better image quality with fewer bits. It has been shown in table-3 that the compression performance of work reported in [14], WDR, SPIHT and JPEG2000 are comparable but in some cases JPEG2000 is little better than WDR, SPIHT and to the work in [14]. Meanwhile, our approach outperforms all the existing methods reported in this work with improved image quality and compression performance. The proposed scheme is applied on all the test images but the values of Lena image is discussed for an instance, when the Lena image is compressed using proposed method, it gives 32.99 db PSNR with 0.5058 bpp, while these figures obtained using recent published work are 31.97 db with 0.8101 bpp. The PSNR and bpp for WDR and SPIHT methods for the same image are 32.48 db and 1.4434 bpp and 32.64 and 1.0505 bpp respectively. While the PSNR and bpp, using state of art JPEG2000 are 32.76 db and 0.6903 bpp respectively. Therefore, it is evident from the average values shown in table-3 that the proposed method improved the image quality with using fewer bits. After checking the efficiency of proposed work over several existing methods, the performance of our approach is measured by using different number of bits for quantization, the results thus obtained are shown in table-4. It is clear from the data shown in table-4 that the values of bpp decreases when the value of quantizing parameter ( b ) decreases. In brief, we can say that the better compression performance can be achieved on decreasing the number of bits with an acceptable quality of reconstructed image. The original test images and reconstructed images of proposed work are shown in figures 4 and 5 respectively, it can be perceptually observed that the human visual system can not found any

significant distinction in the quality of original and reconstructed images, while from the storage point of view reconstructed images take less storage space than the original.

Fig.4. Original test images

Airplane                 Peppers                 Lena

PSNR=30.66,          PSNR=31.05         PSNR=32.99

bpp=0.4799            bpp=0.5659           bpp=0.5058

Girl PSNR=35.89 bpp=0.4281

Ш№

Couple PSNR=32.96 bpp=0.5970

House PSNR=32.76 bpp=0.5191

Zelda PSNR=31.98 bpp=0.6001

Fig.5. Reconstructed images

An efficient color image compression technique using IWT and prediction error is proposed. In our approach the correlation among the RGB planes is reduced using YCoCg-R transform, which transforms the R, G, B color space to less correlated Y, Co, Cg color space losslessly. The good performance of proposed work is due to the

low computational complexity of both YCoCg-R and IWT. The efficiency of proposed work is evaluated by comparing it with several DCT and wavelet based compression methods including standard JPEG2000. It is found experimentally that the performance of proposed work is superior not only to the elaborated methods but also to the state of art work i.e. compression standard JPEG2000. The proposed scheme can compress the images losslessly when 8 bit quantizer is used, which gives us a direction to focus on lossless compression of color images in future. The analysis of proposed method showed that our approach outperforms the several existing methods in the case of lossy color image compression, but its performance can be improved for the case of lossless compression.

• [1]    W. B. Pennebaker and J. L. Mitchell, “JPEG Still Image Data Compression Standard”, Van Nostrand Reinhold , 1993.

• [2]    “Information Technology- Lossless and Near-Lossless Compression of Continuous-Tone Still Images (JPEG-LS)”, 1993.

• [3]    M. Weinberger, G. Seroussi and G. Sapiro, “The LOCO-I lossless image compression algorithm: Principles and standardization into JPEG-LS”, IEEE Trans. Image Process, Vol. 9, 1309–1324, 2000.

• [4]    X. Wu and N. Memon, “Context-based adaptive loss-less image coding”, IEEE Trans. Commun ., 437-444, 1997.

• [5]    ISO/IEC and ITU-T, “Information Technology JPEG2000 image coding system: core coding sys-tem”, ISO/IEC International Standard 15444-1 and ITU-T recommendation, 2004.

• [6]    ITU-T and ISO/IEC, “JPEG XR image coding systemPart 1:Core Coding System”, Image coding Specification , 2011.

• [7]    E.J. Delp and O.R. /mitchell, “Image compresion us-ing block truncation”, IEEE Transactions on Communications , vol. 27, 1335-1342, 1979.

• [8]    T. Kurita and N. Otsu, “A method of block truncation coding for color image compression ”, IEEE Transac-tions on Communications , vol. 41, 1270-1274, 1943.

• [9]    Y. Wu and D.C. Coll, “Single bit map block trunca-tion coding for color  image”,   IEEE Transactions on

  Communications , vol. 35, 1987.

• [10]    S.C. Tai, Y.C. Lin and J.F. Lin, “Single bitmap block truncation coding of color image using hopfield neu-ral network”, Inform. Sci ., 103, 211-218, 1997.

• [11]    B. Dhara and B. Chanda, “Color image compression based on block truncation coding using pattern fitting principle”, Pattern Recognition ,  vol. 40, 2408-2417, ,

  • [12]    C. Yang, J. Lin and W. Tsai, “Color image com-pression by moment-preserving and block trunca-tion coding techniques”, IEEE Transactions on Communications , vol. 45, 1513-1516, 1997.

  • [13]    S.I. Olsen, “Block truncation and planar image coding”, Pattern recognition letter , vol. 21, 1141-1148, 2000.

  • [14]    F. Douak, R. Berizid and N. Benoudjit, “Color image compression algorithm based on the DCT transform combined to an adaptive block scanning”, Int. J. Electron. Commun , vol. 65, 16–26, 2011.

  • [15]    Y. Feng and N. Nasrabadi, “Dynamic address-vector quantisation of RGB colour images”, IEE Proceed-ings Communications Speech and Vision, vol. 238, 225-231,

    • [16]    W. Lee and C. Chan, “Dynamic finite state VQ of colour images using stochastic learning”, Signal Pro-cessing: Image Communication , vol. 6, 1–11, 1994.

    • [17]    S. Makrogiannis, G. Economou and S. Fotopoulos, “Region oriented compression of color images using fuzzy inference and fast merging”, Pattern Recognition , vol. 35, 1807–1820, 2002.

    • [18]    A. Alkholidi, A. Alfalou and H. Hamam, “A new approach for optical colored image compression using the jpeg standards”, Signal Processing, vol. 87, 569–5839, 2007.

    • [19]    D. Chikouche, R.Benzid and M. Bentoumi, “Application of the dct and arithmetic coding to medical image compression”, International conference on in-formation and communication technologiess: from theory to applications (ICTTA) , 1-5 , 2008.

    • [20]    W. Yu and F. Sun,J. Fritts, “Efficient rate control for jpeg2000”, IEEE Transactions on Circuits and Sys-tems for Video Technology , vol. 16, 577-589, 2006.

    • [21]    A. Skodras, C. Christopoulos and T. Ebrahimi, “Jpeg2000: the upcoming still image compression standard”, Pattern Recognition Letters , vol. 22, 1337-1345, 2001.

    • [22]    W. Pearlman, A. Islam, N. Nagaraj and A. Said, “Efficient, low-complexity image coding with a setpartitioning embedded block coder”, IEEE Transac-tions on Circuits and Systems for Video Technology , vol. 14, 1219-1235, 2004.

    • [23]    A. badpour and S. Kasaei, “Color PCA eigen images and their application to compression and watermarking”, Image and Vision Computing , ol. 26, 878-890, 2008.

    • [24]    J. M. Shapiro, “Embedded image coding using ze-rotrees of wavelet coefficients”, IEEE Trans. Signal Process ., vol. 41(12), 3445-3462, 1993.

    • [25]    A. Said and W. A. Pearlman, “A new, fast and efficient image codec based on set partitioning in hi-erarchical trees”, IEEE Transactions on Circuit and System for Video Technology , vol. 7(3), 242-250, 1996.

    • [26]    E. Ordentlich and M. Weinberger and G.Seroussi, “A low-complexity modelling approach for embedded coding of wavelet coefficients”, Proceeding of IEEE Data Compression Conference , 408-417, 1998.

    • [27]    J. S. Walker and T. Q. Nguyen, “Wavelet based image compression”, chap. 6, in: K.R. Rao, P. Yip (Eds), Handbook on transform and data compression CRC press Boca Raton , 267-312, 2001.

    • [28]    Y. Yuan and M. K. Mandal, “Noval embedded image coding algorithms based on wavelet difference reduction”, Vision, Image and Signal Processing, IEE Proceedings , vol. 152(1), 9-19, 2005.

    • [29]    J. S. Walker, “Lossy image codec based on adaptively scanned wavelet difference reduction”,   Optical En

      gineering, Optical Engineering , vol. 39(7), 1891-1897, 1995.

• [30]    J. S. Walker and T. Q. Nguyen, “Adaptive scanning methods for wavelet difference reduction in lossy image compression”, Proceeding of IEEE Interna-tional Conference on Image Processing , 3, 182-185, 2000.

• [31]    A. R. Calderbank, I. Daubechies, W. Sweldens and B. L. Yeo, “Wavelet transforms that map integers to integers”, Appl. Comput. Harmonics Anal , vol. 5, 332-369, 1998.

• [32]    I. Daubechies and W. Sweldens, “Factoring wavelet transforms into lifting steps”, J. Fourier Anal. Appl , vol. 4, 245-267, 1998.

• [33]    W. Sweldens, “The lifting scheme: a construction of second generation wavelets”, SIAM J. Math. Anal., vol. 29, 511-546, 1998.

• [34]    Henrique S. Malvar, Gary J. Sullivan and Sridhar Srinivasan, “Lifting-based reversible color transformations for image compression”, Proc. SPIE, 2008.

• [35]    B. Yuan and X. Tang “(Eds., Image data processing in the compressed wavelet domain”, 3rd International Conf. on Signal Processing Proc. , vol. 147, 978-981, 1996.

• [36]    S. C. Pei and J. J. Ding, “Reversible Integer Color Transform”, IEEE Transactions on Image Processing , vol. 16, 1686–1691, 2007.

• [37]    I. Singh, P. Agathoklis and A.Antoniou, “A Loss-less compression of color images using an improved integerbased nonlinear wavelet transform”, IEEE international symposium on circuits and systems , 1997.

• [38]    R. Starosolski, “New simple and efficient color space transformations for lossless image compression”, J. Vis. Commun. Image, vol. 25, 1056–1063, 2014.

• [39]    S. Kumari “A Wavelet Based Approach for Compression of Color images”, I.J.Modern Education and Computer Science, Vol. 1, 28-35, 2013.

• [40]    B. Mohammed, Performance Comparison of DWT compared to DCT for Compression of Biomedical Images,”, I.J.Modern Education and Computer Science, Vol. 4, 9-16, 2014.