m-aperiodic words on three-letter alphabet

The work is devoted to the study of sets of aperiodic words over a finite alphabet. The set of aperiodic words can be considered as a dictionary of some finite formal language.

Data on the existence of an infinite word in a two- or three-letter alphabet, which does not contain subwords that are cubes or, respectively, squares, were first obtained by A. Thue in 1906. [1]. An example of an infinite sequence of irreducible words, each of which is the beginning of the next and does not contain squares of words in an alphabet of two letters, was constructed by S. I. Adyan (Lemma 1 from [2]). In an article by S. E. Arshon in 1937. [3] the existence of an n-digit asymmetric repetition-free sequence for an alphabet of at least three letters has been proven. In the monograph by S. I. Adyan [4] it has been proven that in an alphabet of two symbols there exist infinite 3-aperiodic sequences. The problem of studying such sequences is considered by S. I. Adyan in connection with his study of the Burnside problem [5–7]. A. M. Shur found out which properties of ordinary words are preserved during the transition to infinite ones, and which ones are modified, lost or replaced by new ones, and studied the set of all cubeless Z-words in a two-letter alphabet [8–10]. In the monograph by A. Yu. Olshansky [11], the infinity of the set of 6-aperiodic words in a two-letter alphabet was proved and an estimate was obtained for the number of such words of any given length.

We have improved A. Yu. Olshansky’s estimate [11] of the number of 6-aperiodic words in the 2-letter alphabet [12], and also made a report on the topic of aperiodic words [13]. Then research on this issue continued.

In [14], a theorem was proven about the infinity of the set of m-aperiodic words for m ≥ 4 in a two-letter alphabet and an estimate of the number of such words was obtained. The case of a three-letter alphabet was considered only in one case: in [15], an estimate was obtained for the number of 6-aperiodic words.

In this article, the set of m-aperiodic words in the three-letter alphabet will be studied: the infinity of the set of m -aperiodic words for m ≥ 4 i n three letters alphabet and an estimate of the number of such words was obtained. The results may be useful when encoding information in space communication sessions.

Generalizations of aperiodicity, when not only the powers of some subwords are excluded, were studied in [16].

Main result

We consider that a periodic word with period H is any subword of some word Н^р , р > 0 .

As an example of a periodic word with period ab, we consider the word ababa .

A l-aperiodic word is a word X in which there are no nontrivial subwords of the form Y^l.

• S. I. Adyan [4] proved that in an alphabet of two letters there are infinitely many arbitrarily long 3-aperiodic words.

• S.    E. Arshon established the existence of words of any length free from squares in a three-letter alphabet [3].

A. Yu. Olshansky in [11] considered a set of 6-aperiodic words. He proved that such words of any length exist and obtained an estimate for the function ^{f ( n )} – number of 6-aperiodic words of length n . There were more of them than ( 32 ) . In [12], we improved A. Yu. Olshansky’s estimate of the number of 6-aperiodic words over a 2-letter alphabet.

In [15], we proved a theorem about the infinity of the set of m-aperiodical words under a period limitation m >  4 in a two-letter alphabet and obtained a lower estimate for the number of such words.

It is of interest to us to estimate the number of m -aperiodic words in an alphabet of three letters. When proving the theorem, we will use the method used by A. Yu. Olshansky [11].

Theorem. In the three-letter alphabet there are arbitrarily long m-aperiodical words for m >  4 and number f ( n ) there are more such words of length n than ( 52 ) .

Proof . We consider the three-letter alphabet { a , b , c }. In this alphabet we will study m-aperiodic words for m >  4 . We will investigate the function f ( n ) number of m- aperiodic words of length n .

First we prove the inequality f ( n + 1) >  (5/2) f ( n ) using the method of mathematical induction.

We note that there are exactly three m -aperiodic words a , b , c of length one and nine m -aperiodic words aa , ab , ac , ba , bb , bc , ca , cb, cc of length 2 in the three-letter alphabet for m >  4 . Thus, in this case we have f (1) = 3, f (2) = 9 .

Then for n = 1 the inequality holds f (2) > 52 • f (1) and the resulting estimate is as a base of induc- tion

Now we need to take the induction step. We assume that the inequality f ( n ) >  (5/2) f ( n - 1) is true for all values not exceeding n , and establish its validity in the case f ( n + 1) > (5/2) f ( n ).

Any m -aperiodic word of length n + 1 can be obtained by assigning the letters a , b or c to the right of the m -aperiodic word of lengt n . This produces 3 f ( n ) words of X length n + 1 .

Some of these words contain degrees A ^m . We try to discard such words containing subwords of period m.

When assigning a new letter to the right, you can only get a word like X = YA ^m ,containing a word of period m , since otherwise the beginning of length n of the word X of length n + 1 contains a periodic subword of period m : A ^m .

For words A of length 1 (there are only three such words), there are at most 3 f ( n - m + 1) words of X = YA ^m type, where the word Ym is aperiodic and | h | = n - m + 1, A is one of the words a , b , c.

As shown above, there are only nine words A of length 2. Then the number of words of the form X = YA ^m length n + 1 is no more than 9 f ( n - 2 m + 1), where the word Y is m -aperiodic and has a length n - 2 m + 1.

We further reason in the same way and obtain an estimate for the number of words of length n + 1 (a strict inequality, since it is easy to indicate words that, when obtaining an estimate for the number of words of the form X = YA ^m , already with a length of 1 word A, we discarded in excess to obtain an estimate):

f ( n + 1) >  3 f ( n ) - 3 f ( n - m + 1) - 3 ² f ( n - 2 m + 1) - 3 3 f ( n - 3 m + 1) - ...

Since the estimate is valid by inductive assumption f ( n ) >  ( 52 ) • f ( n - k ), applying it, we see:

( I r /\-m + 1              r /\“2m + 1             c /X~mm + 1           A f (n +1) > 3 f (n) - ^ 3( 52)    f (n) + 32 (52)     f (n) + 33 (5/)     f (n) +... J.

We transform the resulting inequality:

(      /\-m+1    о / с /\—2m+1     э / с /\—3m+1     А f (n +1) > f (n)(3-^3(52)    + 3 2 (52)     + 3 3 (52)     +...j .

Obviously, m3 < 52, therefore the geometric progression in brackets is decreasing with the de- nominator 3

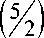
- m

with the limitation m >  4 .

For the expression S in parentheses on the right side, we apply the formula for the sum of a decreasing geometric progression

S = 3 -

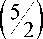
- m +1

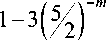
To prove the theorem, we need an estimate of the expression in brackets on the right side of the inequality S >  52 .

We substitute the expression obtained above for S into the inequality and perform elementary transformations:

- m

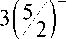
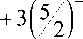
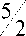
1 - 3

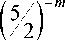
> 0.

We will simplify the resulting inequality:

Since the inequality 1 - 3

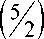
- m

3 - 9

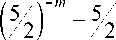
1 - 3

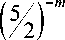
> 0.

> 0 holds for m >  4, it remains to check the validity of the ine-

quality :

3 - 9

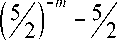
> 0.

The validity of this inequality is established by direct calculation at m = 4, and m > 4 at it is even more true, since

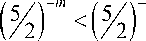
for such m. Consequently, it has been proven that the inequal- ity f (n +1) > 52 f (n) holds for any natural values of the number n, subject to m > 4 .

The theorem is proven.

Conclusion

The question of estimating the number of aperiodic words under various conditions continues to be studied. The set of m -aperiodic words for m >  4 in a three-letter alphabet is considered and an estimate is obtained for the function of the number of such words of any given length.

Acknowledgment. The work was performed in the framework of the state assignment of ICM SB RAS, project no. 0287-2021-0002. This work is supported by the Krasnoyarsk Mathematical Center and financed by the Ministry of Science and Higher Education of the Russian Federation (Agreement No. 075-02-2024-1429).