M-апериодические слова над трехбуквенным алфавитом

Работа посвящена изучению множеств апериодических слов над конечным алфавитом. Множество апериодических слов можно рассматривать как словарь некоторого конечного формального языка.

Данные о существовании бесконечного слова в двух- или трехбуквенном алфавите, которое не содержит подслов, являющихся кубами или, соответственно, квадратами, впервые получены А. Туэ в 1906 г. [1]. Пример бесконечной последовательности несократимых слов, каждое из которых является началом следующего и не содержит квадратов слов в алфавите из двух букв, построил С. И. Адян (лемма 1 из [2]). В статье С. Е. Аршона 1937 г. [3] доказано существование n -значной ассиметричной бесповторной последовательности для алфавита не менее чем из трех букв. В монографии С. И. Адяна [4] доказано, что в алфавите из двух символов существуют бесконечные 3-апериодические последовательности. Задача изучения таких последовательностей рассматривается С. И. Адяном в связи с его исследованием проблемы Бернсайда [5–7]. А. М. Шур выяснил, какие свойства обычных слов сохраняются при переходе к бесконечным, а какие видоизменяются, теряются либо заменяются новыми, и изучил множество всех бескуб-ных Z-слов в двухбуквенном алфавите [8–10]. В монографии А. Ю. Ольшанского [11] доказана бесконечность множества 6-апериодических слов в двухбуквенном алфавите и получена оценка количества таких слов любой данной длины.

Нами была улучшена оценка А. Ю. Ольшанского [11] количества 6-апериодических слов в 2-буквенном алфавите [12], а также сделан доклад по теме апериодических слов [13]. Затем исследования по этому вопросу были продолжены.

В работе [14] доказана теорема о бесконечности множества m -апериодических слов для m ≥ 4 в двухбуквенном алфавите и получена оценка количества таких слов. Случай трехбуквенного алфавита рассмотрен только в одном случае: в работе [15] получена оценка для количества 6-апериодических слов.

В данной статье будет изучено множество m -апериодических слов в трехбуквенном алфавите: доказана бесконечность множества m -апериодических слов для m ≥ 4 в трехбуквенном алфавите и получена оценка количества таких слов. Результаты могут быть полезны при кодировании информации в сеансах космосвязи.

Обобщения апериодичности, когда исключаются не только степени некоторых подслов, исследовались в [16].

Основной результат

Напомним, что периодическим словом с периодом Н называется любое подслово некоторого слова Н ^р , р > 0 .

В качестве примера периодического слова с периодом ab можно рассмотреть слово ababa. l-апериодическим словом называется слово Х , в котором нет нетривиальных подслов вида Y ^l .

• С. И. Адян [4] доказал, что в алфавите из двух букв существует бесконечно много сколь угодно длинных 3-апериодических слов.

С. Е. Аршон установил существование слов любой длины, свободных от квадратов в трехбуквенном алфавите [3].

А. Ю. Ольшанский в работе [11] рассматривал множество 6-апериодических слов. Он доказал, что существуют такие слова любой длины, и получил оценку функции f (n) – количества 6-апериодических слов длины n. Их оказалось больше, чем (У) . В работе [12] нами улуч- шена оценка А. Ю. Ольшанского количества 6-апериодических слов над 2-буквенным алфавитом.

В работе [15] нами доказана теорема о бесконечности множества m -апериодических слов при ограничении на период m >  4 в двухбуквенном алфавите и получена оценка снизу количества таких слов.

Для нас представляет интерес оценить количество m -апериодических слов в алфавите из трех букв.

При доказательстве теоремы мы будем применять метод, используемый А. Ю. Ольшанским [11].

Теорема. В трехбуквенном алфавите существуют сколь угодно длинные m-апериодические слова для m > 4 и число f (n) таких слов длины n больше, чем

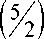
Доказательство. Рассмотрим трехбуквенный алфавит {a, b, c}. В этом алфавите будем изучать m-апериодические слова для m > 4 . Будем исследовать функцию f (n) количества m-апериоди- ческих слов длины n.

Сначала докажем неравенство f ( n + 1) >  (5/2) f ( n ) при помощи метода математической индукции.

Заметим, что имеется ровно три m -апериодическиx слова a , b , c длины один и девять m -апериодических слов aa , ab , ac , ba , bb , bc , ca , cb , cc длины 2 в трехбуквенном алфавите для m >  4 . Таким образом, в этом случае имеем f (1) = 3, f (2) = 9 .

Тогда при n =1 справедливо нервенство f (2) >  52 • f (1) и полученная оценка выступает в качестве базы индукции.

Теперь нужно сделать шаг индукции. Предположим, что неравенство f ( n ) >  (5/2) f ( n - 1) верно для всех значений, не превышающих n , и установим его справедливость в случае f ( n + 1) >  (5/2) f ( n ).

Любое m -апериодическое слово длины n + 1 можно получить приписыванием справа букв a, b или c к m -апериодическому слову длины n . Так получается 3 f ( n ) слов X длины n + 1.

Некоторые из таких слов содержат степени A ^m . Попробуем отбросить такие слова, содержащие подслова периода m .

При приписывании новой буквы справа может получиться только слово вида X = YA ^m , содержащее слово периода m , так как иначе начало длины n слова X длины n + 1 содержит периодическое подслово периода m: A ^m .

Для слов A длины 1 (существует всего три таких слова) имеется не больше, чем 3 f ( n - m + 1) слов вида X = YA m , где слово Y m -апериодично и | У | = n — m + 1, A - одно из слов a , b , c.

Как показали выше, существует всего девять слов A длины 2. Тогда количество слов вида X = YA m длины n + 1 не больше, чем 9 f ( n — 2 m + 1), где слово Y m -апериодично и имеет длину n — 2 m + 1.

Рассуждаем далее таким же образом, получаем оценку количества слов длины n +1 (строгое неравенство, так как легко указать слова, которые при получении оценки количества слов вида X = YA ^m уже при длине 1 слова A мы отбросили с избытком для получения оценки):

f ( n + 1) >  3 f ( n ) - 3 f ( n - m + 1) - 3 2 f ( n - 2 m + 1) - 3³ f ( n - 3 m + 1) - ...

Так

как по индуктивному предположению справедлива оценка

f ( n ) > ( 52 ) ’ f ( n - к),

то

применяя ее, видим:

f ( с /\- m + 1               c /\-2 m + 1              с /\-3 m + 1           A

f ( n + 1) >  3 f ( n ) - ^ 3 ( 52 )     f ( n ) + 3 2 ( 52 )      f ( n ) + 3 3 ( 52 )      f ( n ) + ... j .

Преобразуем полученное неравенство:

( I с /\-m+1    n r /\_2m+1       r /\_3m+1     A f (n+1) > f (n )(3-^ 3( 52)    + 32 (52)     + 33 (52)     +...].

Очевидно, m 3 <  52

поэтому геометрическая прогрессия в скобках является убывающей со знаменателем

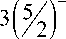
при ограничении m >  4 .

Для выражения S в скобках правой части применим формулу суммы убывающей геометрической прогрессии

S = 3 -

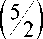
- m + 1

1 - 3

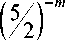
Для доказательства утверждения теоремы нам требуется оценка выражения в скобках правой части неравенства S >  52 •

Подставим в неравенство полученное выше выражение для S и выполним элементарные преобразования:

3 - 9

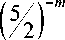
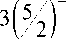
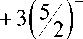
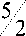
1 - 3

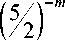
> 0.

Упростим полученное неравенство:

Так как неравенство 1 - 3

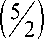
- m

3 - 9

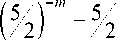
1 - 3

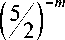
> 0.

> 0 выполняется при m >  4, то остается проверить справед-

ливость неравенства:

3 - 9

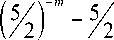
> 0.

Справедливость этого неравенства устанавливается непосредственным вычислением при m = 4, а при m > 4 оно тем более верно, поскольку

( 52 )' m < ( 522 )■³

при таких m . Следователь-

но, доказано, что неравенство f (n +1) > 52 f (n) выполняется для любых натуральных значений числа n при условии m > 4 .

Утверждение теоремы доказано.

Заключение

Продолжается изучение вопроса об оценке количества апериодических слов при различных условиях. Рассмотрено множество m -апериодических слов при m ≥ 4 в трехбуквенном алфавите и получена оценка для функции количества таких слов любой данной длины.

Acknowledgment. The work was performed in the framework of the state assignment of ICM SB RAS, project no. 0287-2021-0002. This work is supported by the Krasnoyarsk Mathematical Center and financed by the Ministry of Science and Higher Education of the Russian Federation (Agreement No. 075-02-2024-1429).